|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(2); 2018 > Article |
|
Abstract
There are various methods for the rainfall time distribution and numerous theoretical approaches have been proposed in many countries. The fact, however, is that only used model in each country are presented as official guidelines. In Korea, the Huff’s method is generally used, but several problems have been proposed. Therefore, in this study, we developed the time distribution method using actual rainfall and verify its applicability. It is very reasonable to utilize the time distribution pattern which reflects the regional rainfall characteristics for designing the structures. In this study, a total of 172,851 storm events were extracted from 69 meteorological stations, and the hourly maximum rainfall over 30mm was separated to analyze the each event. Considering actual rainfall characteristic to drive the time distribution, we suggested the conditions and constraints to distribute the rainfall. Additionally, the constraint time distribution method can be applied to cases where peak runoff and runoff volume are crucial.
요지
해외 많은 연구에서 다양한 시간분포 방법론이 이론적으로 제시되었으나 실질적으로 해당국가에서 사용하고 있는 시간분포 모형은 국가기관의 공인된 가이드라인으로 제시된 방법을 일괄적으로 적용하고 있다. 우리나라의 경우에는 일반적으로 Huff 방법을 사용하고는 있으나 여러 문제점이 제기되고 있는 바 이를 보완하고자 본 연구에서는 실측 강우를 이용한 시간분포 방법을 개발하여 그에 대한 적용성을 검토해 보았다. 구조물의 설계를 목적으로 강우량을 시간분포 시킬 때 지역적 강우 특성을 반영한 시간분포 형태를 활용하는 것은 매우 합리적이다. 본 연구에서는 기상청 69개 지점에서 총 172,851개의 호우사상을 추출하여, 이중 시간최대 강우량이 30 mm 이상인 호우사상을 분리하여 사상별로 분석을 실시하였다. 실제 우리나라의 강우특성이 반영된 시간분포를 도출하여, 시간분포 방법 결정시 고려해야 할 조건 혹은 제약사항을 제시하였다. 그리고, 제약조건에 따른 강우 시간분포 방법을 첨두유출량과 유출용적이 중요한 경우에도 적용이 가능하도록 하였다.
통상 국내에서는 특정 빈도에 해당하는 설계 홍수량 또는 유량은 자료 부족으로 인해 홍수량의 빈도해석 결과보다는 강우자료를 분석하여 강우-유출 관계에 따라 도출되는 것이 일반적이다. 최근 호우의 시간분포 경향을 보면 1시간 최대강우량 보다 3∼6시간 최대 강우량이 평균 재현기간이 더 큰 경향을 나타내고 있다. 따라서, 최근에는 저류형 내수배제시설과 저수지 등에서도 유출 체적 뿐만 아니라 유출수문곡선이 필요한 바, 합리식보다는 단위도법이나 강우-유출모의 모형이 개발되어 사용되고 있다. 이러한 방법으로 수공구조물 설계를 위한 설계우량에 따른 세밀한 유출수문곡선의 합성이 필요하다. 특히 선정된 빈도와 지속기간에 대한 설계우량의 우량주상도 기준, 즉 설계호우의 시간 분포는 수공구조물 설계에 있어 중요한 요소이다.
설계 강우의 시간분포 양상은 설계지역의 과거 강우자료로부터 강우 지속기간 동안에 총 강우량이 시간이 경과함에 따라 어떻게 분포하는가를 통계학적으로 분석하여 그 지역에 적합한 시간분포 모형을 만들어 수공구조물의 설계조건에 따라 결정한다.
국내에서는 Park et al.(1981)이 서울 지점에 대하여 Huff(1967)의 4분위법에 의해 시간분포를 분석한 바 있고, Seo et al.(1981)은 이 연구결과를 이용 도시유역모형인 TRRL 모형(Transportation & Road Research Laboratory Model)에 적용한 바 있다. 또한, Lee(1983)도 Huff(1967)의 4분위법에 의해 총우량 80mm 이상의 호우를 선별 전국적인 분석을 하였다. 여기에서 그는 국내는 대체로 제 3구간 호우가 지배적이고, 지속기간에 따른 누가확률곡선의 영향은 크지 않다고 제시하였다. 그리고 건설교통부(2000)는 「지역별 설계강우의 시간적 분포」에서 기상청 산하 69개 관측소의 자기우량기록지에서 읽은 10분 단위 우량자료를 가지고 앞에서 설명한 Yen & Chow, Huff, Keifer & Chu, 그리고 Pilgrim & Cordery 방법을 이용하여 해석하고 그 이용 방법과 각 방법에 따른 기준치를 제시한 바 있다.
본 연구에서는 우리나라에서 발생한 강우의 시간분포 특성을 분석하여, 실제 우리나라에서 발생한 극한 호우사상에 근거한 경험적 시간분포를 유도하여 제시하였다. 실제 강우특성이 반영된 시간분포를 도출하여, 실제 설계시 강우의 시간분포를 조건 및 제약사항에 따라 적용하는 방안에 대하여 검토해 보았다.
본 연구에서는 우리나라 기상청 관할 관측소 시자료(최대관측기간 1961년∼2010년, 69개 지점) 중 시간최대 강우량이 0.5mm 이상인 사상에 대해 무강우 지속기간 따른 강우 지속기간별 강우자료의 시간분포 특성과, 무강우 지속기간 6시간의 경우에 시간최대 강우량에 따른 강우 지속기간별 강우자료의 시간분포 특성을 분석하였다.
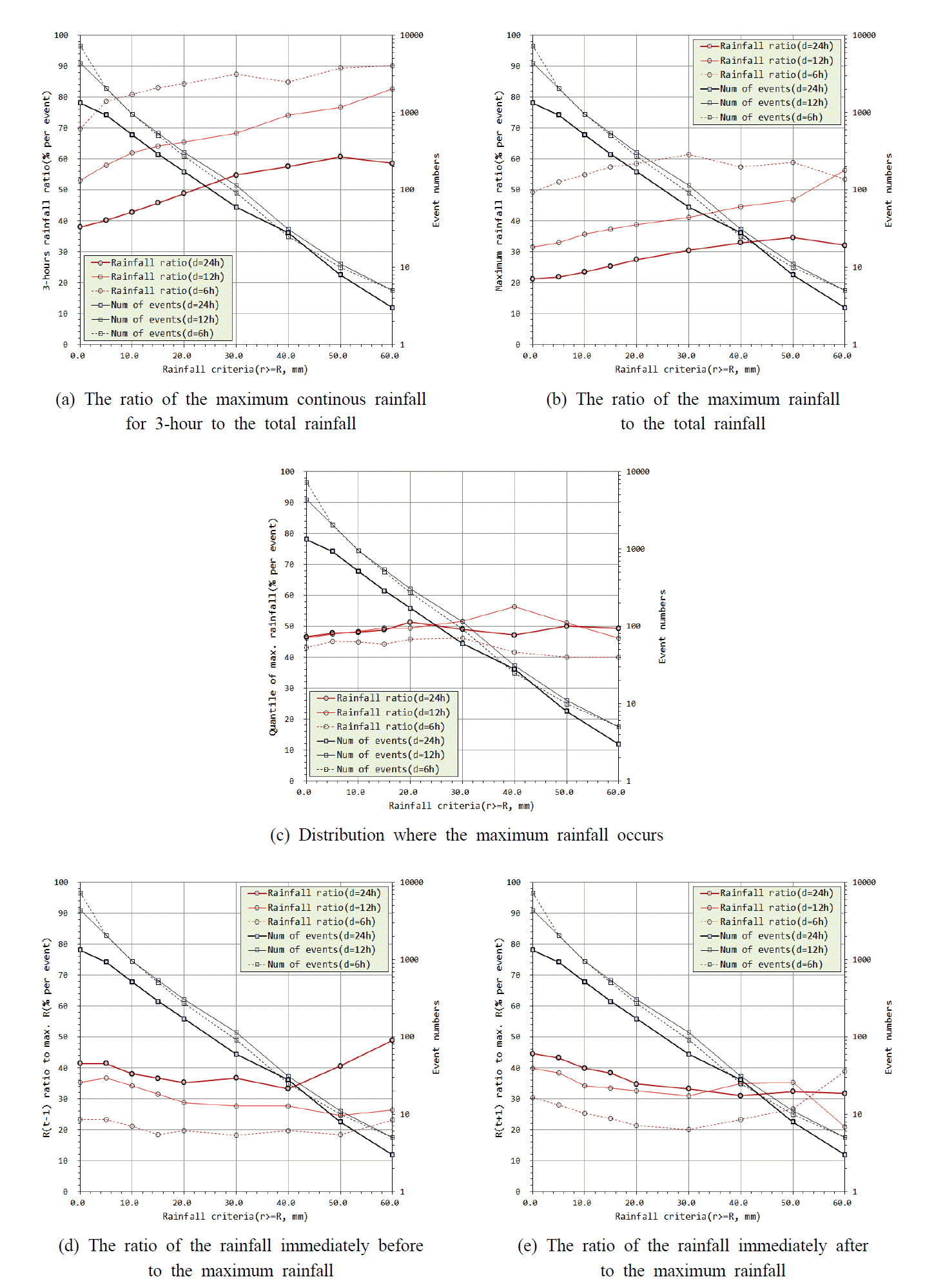
Fig. 1과 같이 강우 지속기간별 총강우량 대비 3시간 연속 최대강우량의 비를 분석하였다. 본 분석의 목적은 우리나라 호우 사상의 경우 첨두부 3시간 총강우량의 비율이 매우 높기 때문에 이를 정량화 하고자 함이다. 사상 평균적으로 지속기간 증가에 따라 총강우량 대비 3시간 연속 최대강우량의 비는 완만하게 감소하는 것으로 나타났다.
다음은 Fig. 2와 같이 강우 지속기간에 따른 최대강우량의 발생 분위를 분석하였다. 본 분석의 목적은 최대강우량의 발생 위치를 파악하기 위함이다. 분석결과 무강우 지속기간 구분에 따른 최대강우량의 발생분위의 차이는 미미하였다. 시간최대 강우량 구분에 따른 최대강우량의 발생분위의 차이도 크지는 않았으나 시간최대 강우량이 커질수록 50%에 가까워지는 것으로 나타났다. 그리고 강우 지속기간의 증가에 따라서도 50%에 가까워지는 경향을 보였으나 사상수의 급격한 감소로 편차가 크게 나타났다.
Fig. 5는 호우 규모별 강우 지속기간에 따른 첨두시간 강우량(시간최대 강우량)이 총강우량에서 차지하는 비율을 분석한 결과이다. 지속기간 증가에 따라 첨두 강우량의 비율은 완만하게 감소하는 것으로 나타났다. 강우 지속기간 12시간의 경우는 시간최대 강우량 규모에 따라 첨두시간 강우량의 비율이 30∼50%, 24시간의 경우는 20∼30% 정도인 것으로 나타났다.
Fig. 6은 앞서 분석한 결과를 정리한 그래프로 무강우 지속기간 6시간 기준, 강우 지속기간 6시간, 12시간, 24시간의 경우에 대하여 시간최대 강우량에 따른 강우특성의 변화를 정리한 것이다. 시간최대 강우량의 크기가 증가함에 따라 호우 사상수는 급격히 감소(대수축 적용)함을 알 수 있다.
시간최대 강우량(최대 시강우량) 30 mm 이상의 호우 사상에 대하여, 총강우량 대비 3시간 연속 최대강우량의 비는 Fig. 6의 (a)와 같이 강우 지속기간 6시간의 경우 약 87%, 12시간의 경우는 약 68% 그리고 24시간의 경우는 약 55%로 나타나 첨두부 3시간 총강우량의 비율이 전체 총강우량 대비 매우 높음을 알 수 있었다. 따라서 다수의 배수 시설이 첨두부 최대 강우량에 초점을 맞춰 설계를 하고 있으나 설계시 3시간 연속강우의 영향도 비중 있게 고려해야 할 필요가 있고 이에 대한 추가적인 연구가 필요하다.
시간최대 강우량 30 mm 이상의 호우 사상에 대하여, 총강우량 대비 첨두 강우량의 비는 Fig. 6의 (b)와 같이 강우 지속기간 6시간의 경우 약 61%, 12시간의 경우 약 41%, 24시간의 경우는 약 30% 정도로 나타났다.
시간최대 강우량의 발생 분위는 그림 Fig. 6의 (c)와 같이 지속기간에 큰 차이를 보이지 않고 대부분 40∼50% 사이에 위치하며 이는 일반적으로 사용하는 중앙 집중형이나 Alternating Block Method (ABM)의 시간배치 형태와 부합하는 결과를 보여주고 있다. 단, 이는 사상 평균적인 개념이므로 첨두부의 배치에 따른 홍수량 민감도 분석은 추가로 연구가 필요하다.
시간최대 강우량 30 mm 이상의 호우 사상에 대하여, 최대강우량 대비 직전⋅직후 시간 강우량의 비는 Figs. 6의 (d)와 (e) 같이 강우 지속시간 6시간의 경우 대략 20%, 12시간의 경우 30%, 24시간의 경우는 30∼40% 정도의 크기를 가지는 것으로 나타나, 평균적으로 강우 지속기간 24시간 강우량의 경우 첨두 전후의 3시간 연속 강우량(3시간 연속 최대 강우량과는 차이가 있을 수 있음)은 첨두 강우량 대비 대략 1.6∼1.8배 정도라 가늠해 볼 수 있다.
구조물의 설계를 목적으로 강우량을 시간분포 시킬 때 지역적 강우 특성을 반영한 시간분포 형태를 활용하는 것은 매우 합리적이다. 이러한 측면에서 Huff의 4분위법은 이론적 시간분포 방법에 비해 상당한 장점을 가지고 있다. 그러나 Huff의 4분위법은 호우의 규모에 대한 시간적, 양적 변화율이 일정하다는 가정에 근거하고 있기 때문에 실무적으로 많은 괴리가 있다는 의견이 제기되어 왔다. 그래서 일정 규모 이상의 호우 사상만을 분석하기 위한 적절한 절단수준(threshold)의 설정이 필요하다는 주장이 설득력을 얻어왔다. Huff도 절단수준을 적용하였으나 절단수준이 미미하여(1 in) 실제 큰 규모의 호우를 구별 목적 보다는 수문학적으로 강우로 볼 수 있는 최소 기준의 적용이라는 측면이 강하다고 추정된다.
미국의 경우 실제 호우를 분석하여 SCS 시간분포형을 개발하여 사용하고 있다. 그러나 지속기간 24시간 시간분포를 제시하고 있는데 반해 최대 1시간 강우가 매우 커서 지속기간 24시간 시간분포라는 의미는 크지 않아 보이며 첨두유출량 중심의 설계 시간분포의 성격을 갖고 있다고 볼 수 있다. 따라서 도달시간이 대략 3시간 이내의 소형 배수 구조물의 설계에 적합하다고 볼 수 있다. 그리고 이 SCS방법은 미국의 강우특성을 반영하였기 때문에 우리나라의 경우에 그대로 적용하기엔 무리가 있다.
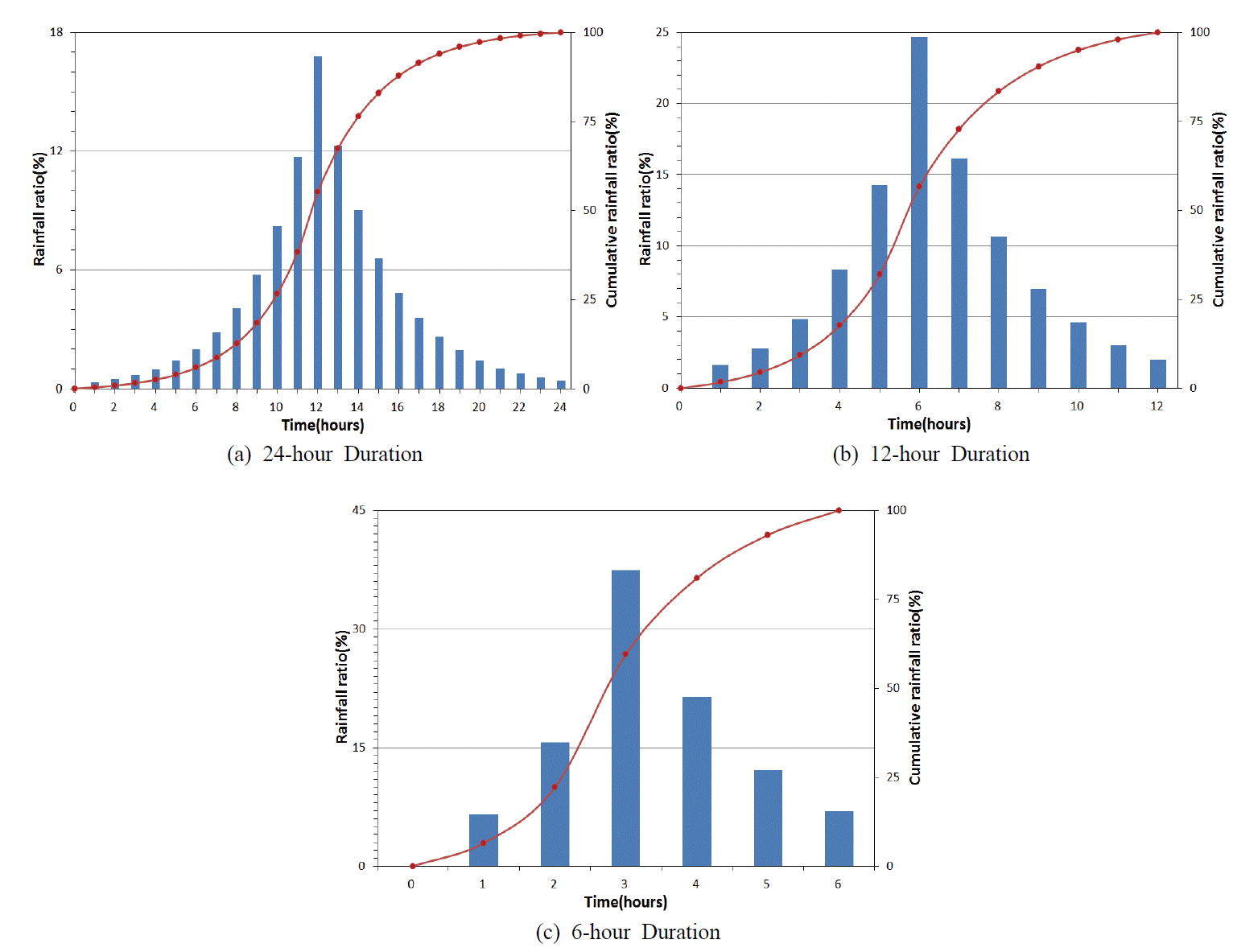
본 연구에서는 실제 우리나라의 강우사상을 분석하여 우리나라 강우특성이 반영된 시간분포를 도출하였다. 그리고 실제 유효 지속기간을 고려하여 첨두유출량과 유출용적이 중요한 경우에도 적용이 가능하도록 하였다. 실제로 설계목적에서 복합호우를 형태를 고려하기 어렵고 지속기간 24시간 이상의 단일호우는 매우 희박하므로 본 분석에서는 24시간, 12시간, 6시간의 세가지 경우로 나누어 시간분포형을 도출하였다. 선정된 지속기간별로 호우사상을 분리함에 있어 대상 지속기간과 가까운 호우사상만을 선정할 경우 실제 지속기간보다 작은 지속기간의 시간분포가 될 수 있다. 실제 호우사상의 시간적인 분포를 분석해 보면 지속기간이 24시간이라 하더라도 호우 첨두부 부근을 제외하곤 매우 작은 강우량을 보이는 경우가 많아 홍수시 구조물에 실질적 부담을 주는 지속기간(유효 지속기간이라 정의)은 이보다 작은 12시간 이내인 것이 보통이다. 따라서 본 분석에서는 사상별로 검토하여 적정 유효 지속기간을 결정한 후 이를 토대로 지속기간별로 구분하였다. Table 1에서 보면 선정된 호우사상의 지속기간이 도출하고자 하는 지속기간보다 큰 것을 볼 수 있는데 유효 지속기간을 고려해 분류했기 때문이다.
본 연구에서는 기상청 69개 지점에서 총 172,851개의 호우사상을 추출하였다. 그리고 이중 시간최대 강우량이 30 mm 이상인 297개 호우사상을 분리하여 사상별로 분석을 실시하였다. 분석결과 형태가 일정하지 않거나 총강우량이 매우 작은 경우(평균 강우강도가 매우 작은 경우) 등 실제 큰 규모의 유출을 유발하지 않을 것으로 판단되는 사상을 제외하고 최종 73개 사상을 선정하여 지속시간별로 분류하였다. 그 결과는 Table 1과 같다.
앞서 분석한 우리나라 시간분포 특성분석에서 평균적으로 첨두 발생분위가 40~50% 사이에 위치하였던 점을 근거로 본 연구에서는 중앙집중형 시간분포를 개발하였다. 그러나 선정된 강우사상은 실측 강우사상이기 때문에 각 강우사상의 시간대별 강우량 조합에 다소의 차이가 있을 수밖에 없다. 그래서 실측사상 그대로 평균적인 시간분포를 도출한다면 이러한 시간분포의 차이로 인해 감쇄효과가 발생할 수 있다. 이러한 감쇄효과로 인해 기왕의 실측 강우사상으로부터 표준시간분포를 도출함에 있어 1개의 대표 강우사상을 추출하여 표준 시간분포로 사용하는 경우 외에는, 재배열 없이 여러 강우사상에서의 평균적인 실측시간 분포의 추출은 불가능하다. 즉, Huff 방법과 같이 평균적인 분포특성을 유도한다면 첨두가 작아지는 것을 피하기는 어렵기 때문에 이것보다는 대표단위도의 유도방법에서와 같이 첨두의 크기는 크기대로 따로 평균하고, 첨두 발생시간은 첨두 발생시간대로 따로 평균하는 것이 좀 더 대표성을 갖게 하는 방법일 것이다. 실제로 우리는 강우량의 크기와 발생시간은 어떤 큰 상관을 가지고 있다고 생각하고 있으나 강우량의 크기와 발생시간은 무관하게 보는 것이 타당하다. 그리고 첨두를 제외한 나머지 부분은 호우사상들의 전체적인 경향을 따르도록 결정할 수 있을 것이다. 따라서 본 연구에서는 실측 강우사상을 중앙을 중심으로 재배열시켜 각 강우사상의 시간 스케일에 따른 강우 스케일의 순서를 일정하게 조율하였다.
그러나 이러한 강우사상의 재배열에 있어서는 반드시 설계측면에서 적절성이 수반되어야 한다. 본 연구에서는 실측 강우 사상을 중앙을 중심으로 크기순으로 재배열 시켰기 때문에 유출량 산정의 측면에서 보면 첨두유량이 가장 큰 경우에 해당하고 양적인 측면에서도 홍수량이 첨두부에 집중되기 때문에 재배열 이전보다 강도가 큰 유출양상을 보이게 된다. 따라서 재배열로 인한 감쇄효과는 발생하지 않는다.
Fig. 7은 이러한 방법으로 산정된 지속기간 24시간의 대표시간분포이고 Fig. 8은 지속시간 24시간의 경우에 ABM(재현기간 100년, Block), SCS 방법(SCS), Mononobe 방법(Mononobe), Huff 방법(2분위, Huff) 시간분포와의 비교이다. 대상지점은 서울의 경우이다. 금회 개발된 시간분포의 경우(Obs)는 첨두부 중심의 ABM, SCS 방법, Mononobe 방법에 비해 약간 완만한 형태를 보이고 있다. 그러나 Huff의 경우와는 확연한 차이를 보이고 있다. 첨두유량 중심의 설계에 있어 Huff의 경우는 다른 방법들과 비교해 첨두유량이 큰 차이를 보일 것으로 판단된다.
본 연구에서 개발된 시간분포의 적용성을 판단하기 위해 실제 호우사상과의 비교를 실시하였다. 2010년 9월과 2011년 7월 서울 일원의 집중호우에 대해 적용하였다. 2010년 9월 호우는 서울 관측소(108) 자료이고 2011년 7월 호우는 남현(425), 관악(509), 서초(401), 강남(400) AWS 자료 및 동두천 관측소(98) 자료이다. Fig. 9는 지속기간 12시간 기준 각 지점별 실측 시간분포를 나타낸다. 그림에서 Seoul은 서울 관측소 자료, Obs는 금회 개발된 시간분포이다. 그림에서와 같이 재배열 시키지 않은 실측사상의 시간분포의 경우(조정전)는 크기별 발생시점이 균일하지 않아 비교가 어렵다.
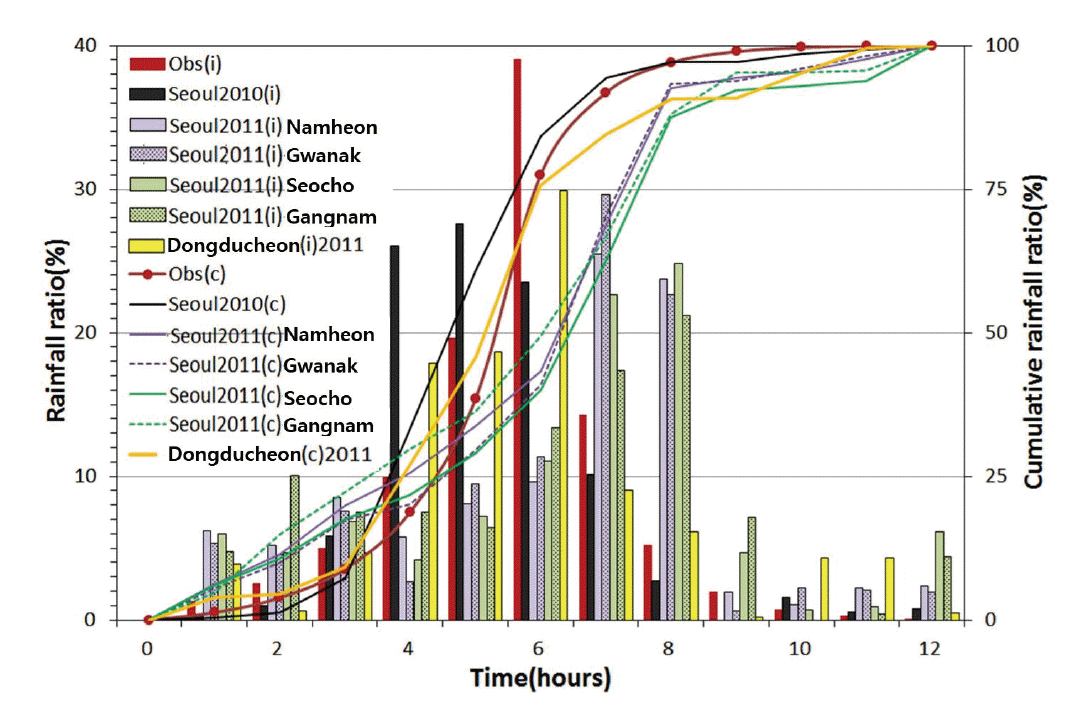
그래서 금회 개발된 시간분포와 동일한 방법으로 각각의 실측사상을 중앙을 중심으로 크기순으로 재배열(조정후)시켰다. Fig. 10은 이렇게 재배열된 실측호우사상의 시간분포와 ABM(재현기간 100년, Block), Mononobe 방법(Mononobe), Huff(Huff(2Q))방법에 의한 시간분포 그리고 금회 개발된 시간분포(Obs)와의 비교이다. i는 시간분포형(incremental distribution)을, c는 누가분포형(cumulative distribution)을 나타낸다. 2010년 실측 호우사상의 경우는 중심부에 호우가 집중된 형태를 보이는데 이는 실제 호우의 강도가 컸기 때문이기도 하지만 유효한 지속기간이 12시간보다 작기 때문이다.
Fig. 11은 좀 더 명확히 비교하기 위해 2011년 호우중 가장 강도가 컸던 동두천, 남현 지점의 실측 시간분포와 기존의 시간분포 그리고 금회 개발된 시간분포만을 비교한 것이다. Fig. 11에서 보듯이 금회 개발된 시간분포는 ABM과 같은 이론 분포 및 최근의 실제 호우의 시간적 분포 특성과도 비교적 잘 일치하고 있다. 좀 더 세밀히 살표보면 첨두 강우량의 경우는 Mononobe 방법(43%), ABM(36%)이 상대적으로 크게 나타났다. 첨두 전후의 3시간 강우량 비중을 보면 실측 분포인 동두천의 경우 전체의 약 66%로 Mononobe 방법(62%), ABM(62%)보다도 약간 크게 나타났고 남현과 금회 개발된 시간분포의 경우는 각각 59%와 56%를 차지했다. 전체적으로 3시간 강우량의 비중은 56%에서 66%로, 실측 호우 사상의 경우 유효 지속기간이 다르다는 점을 감안할 때, 큰 차이를 보이지는 않았다. 그렇다 할지라도 동두천과 같이 실측호우 사상이 가장 크게 나타났다는 것은 최근 우리나라 극치 호우 사상의 경향이 매우 이례적이라는 것을 의미한다. 즉, 2011년 호우 사상의 경우는 지속시간 1시간 보다 3시간의 재현기간이 더 큰 특징을 가지고 있다고 볼 수 있다. 이러한 점은 향후 도시 계획시 도달시간이 짧은 배수 시설 설계시 반드시 염두에 둘 필요가 있다고 사료된다.
금회 도출된 실측 시간분포의 경우는 우리나라 극치 사상의 시간적 분포 특징을 비교적 잘 반영하고 있어 지속기간 12시간에서 24시간 정도의 호우 규모에 대응하는 수공 구조물 설계시 ABM 등의 이론분포와 상호 보완적인 측면에서 병용한다면 유용하게 활용이 가능할 것이다.
지역적 설계강우의 시간적 분포(Ministry of Construction & Transportation, 2000)에서 Huff 방법을 제시한 이후 실무에서 Huff 분포가 거의 표준화되어 사용되어 왔다. 그 동안 많은 연구에서 검토되었지만 Huff 방법도 호우 선정, 평균 방법, 지속기간별 동일 분포 가정 등 여러 가지 문제를 가지고 있어 극치 호우사상을 적절히 모의하지 못하는 약점이 있다는 의견이 많았다. 그럼에도 불구하고 거의 대부분 실무에서 일관되게 Huff 방법을 사용하여 왔다.
일반적으로 첨두 홍수량이 중요한 짧은 지속기간의 호우에서는 ABM을, 유출 용적이 중요한 비교적 긴 지속기간의 호우에서는 Huff 방법이 유용하다고 알려져 있다. 그러나 짧은 지속기간과 긴 지속기간의 기준이 애매하고 경우(지역 및 대상 구조물 규모 등)에 따라 지속기간은 절대기준이 아닌 상대기준이기 때문에 이러한 구분은 의미가 없을 수도 있다.
Huff 방법의 결정적 문제는 분위 선택 보다는 각 분위 자체의 문제로 각 분위에서의 과다 평균으로 인한 평활화 문제라고 봐야 한다. Huff 분포가 실제 극치 사상에 비해 과대 평준화 되어 각 분위별로 곡선이 완만해 어떠한 분위로도 극치사상을 적절히 표현하기가 어려운 경우가 발생한다는 점이다. 단, 실무에서는 강우-유출 산정시 손실우량을 고려해야 하기 때문에 1, 2분위보다는 3, 4분위를 사용하기를 선호하나, 이는 Huff 분위 선택시 중요하게 고려될 사항이긴 하나 Huff 방법 선정의 근거는 될 수 없다.
실무에서 첨두 유량이 수공구조물의 안전에 미치는 영향이 크기 때문에 ABM이나 SCS(NRCS) 시간분포 방법 등 첨두 강우량 중심의 시간분포 방법이 일반적인 수공구조물 설계에서 선호되는 것이 사실이다. 그러나 엄밀히 말해 이러한 방법은 첨두 강우량을 가중한 형태이기 때문에 장기간 지속적인 호우로 인해 강우 지속기간에 따라 재현기간이 증가하는 형태의 강우사상을 모의하는 경우 수문곡선이 왜곡 될 가능성이 있다. 특히, 설정 빈도가 높지 않은 구조물의 경우 경제성 면에서 과대 설계의 우려가 있다. 이러한 측면에서 앞서 언급한 단점에도 불구하고 Huff 방법을 배제할 수 없는 이유이다.
결론적으로 단순히 강우 지속기간 만으로 시간분포 방법을 선정하는 것은 매우 힘들다. 시간분포 선정 시, 정상적인 강우-유출 관계에서, 강우 지속기간 전반적으로 첨두 유출량에 비중을 둔다면 ABM을 우선하여 고려하지 않을 수 없다. 그러나 첨두 유출량에 비중을 두는 경우에도 강우 지속기간 RT 대비 집중시간 TC(혹은 지체시간 TP)의 비율 TC/RT(혹은 TP/RT)이 커지면 ABM과 Huff 방법의 첨두 유출량의 차이는 줄어드는 경향을 보이기 때문에 ABM만을 고려하는 것은 충분치 못하다. 그리고 유출 용적에 비중을 두는 경우에도 구조물의 규모나 특성에 따라 첨두 유출량과 특정 시간구간에서 유출 용적의 크기가 중요할 수 있으므로 ABM과 Huff 방법에 의한 유출 특성의 비교가 필요하다.
그러나, ABM과 Huff 방법을 모두 검토 하더라도 선정기준이 모호하여 분석자마다 판단기준은 작위적일 수 있기 때문에, 논란의 소지는 있으나, 실무적인 측면에서 시간분포방법 결정시 가장 비중 있게 고려해야 할 몇 가지 조건 혹은 제약사항을 제시하고자 한다.
첫째로, ABM의 경우 총 강우량에 해당하는 재현기간이 설정되면 지속기간에 따라 재현기기간도 일정하게 설정되어, 강우 지속기간 증가에 따라 재현기간이 증가하다 감소하는 일반적인 호우 특성과는 차이가 있을 수 있다. 이러한 ABM의 특성 때문에 첨두부는 평균적으로 실제 호우의 재현기간에 비해 크게 산정되고 첨두부에서 멀어질수로 과소 산정될 가능성은 커지게 된다. 이러한 특성을 고려할 때 ABM의 경우는 안전성 면에서 높은 설계 빈도를 요구하는 수공 구조물의 설계에 적용하는 것이 보다 적절할 것으로 판단되나, 이 경우에도 첨두부 과대 추정으로 인해 특정 구간에서 유출량 혹은 유출 용적이 오히려 과소하게 추정될 수도 있으므로 분석시 이에 대한 주의가 필요하다.
예외적으로, 저류능력이 작은 도심지 중소규모 배수시설물의 경우는 첨두 유량이 시설물의 기능에 결정적인 영향을 미치고 기능 상실시 피해가 연쇄적임을 감안할 때 다소 첨두부가 과대 추정되는 경향이 있더라도 ABM를 적용하는 것이 합리적이라 사료된다. 단, 유역면적이 수 km2에 불과한 소규모 배수구역과 같이 유역면적이 작아 강우 지체시간이수 시간 이내인 경우 유출 계산을 위한 강우의 단위 시간간격을 1시간 이내로 설정하게 되면, 임계지속기간이 짧아 동일한 지속기간에서의 ABM 보다 Huff 방법에서 큰 유출이 산정되기도 하는데, 이러한 현상은 강우 지속기간이 짧을 때 Huff 분포의 가로 시간축이 축소되는 효과가 발생하여 ABM과 Huff 분포가 유사한 형태를 가지게 되기 때문이다. 그러나 엄밀히 말해 대부분 Huff 분포의 경우 시간단위 자료를 이용하여 유도되었으므로 단위 시간간격을 시간단위 이하로 설정하는 것은 외삽에 해당하기 때문에 이러한 경우 Huff 방법 적용시 산정 결과의 불확실도가 커질 수 있어 ABM을 적용하는 것이 보다 적절하다고 사료된다.
둘째로, Huff 방법 선택시 분위 선정에 있어서는 2분위와 3분위가 적절할 것으로 보이며 집중시간이 긴 경우에는 4분위도 검토가 필요하다고 판단된다. 최빈분위와 최적분위는 다를 수 있고 2분위와 3분위의 차이는 실제 유효우량 산정 시 초기손실 부분을 제외하면 첨두 유출량 발생시간외에 산정된 첨두 유출량이나 유출 용적에는 큰 차이를 보이지 않으므로 일반적인 경우 실무적으로 3분위가 2분위 보다 안전측일 가능성이 높다고 사료되는 바 분석자가 이러한 점을 고려하여 합리적으로 선정하면 될 것으로 판단된다.
셋째로, 가능한 경우 ABM과 Huff 분포와 본 연구에서 제시한 실측 시간분포에 의한 유출해석 결과를 비교 검토하여 실제 호우사상의 특성을 적절히 반영하는지에 대한 검증이 수반되어야 한다. 더불어, 가장 중요한 점은, 실측 홍수에 의한 설계 홍수량이 부재한 현실에서 강우-유출 해석의 한계를 간과해서는 안 된다. 즉, 현실적으로 경우에 따라 최적시간분포는 달라질 수 있어 이러한 일반적인 기준이 모든 경우에 최선의 선택일 수는 없으므로 강우-유출 관계가 복잡할수록 다양한 방법에 의한 검토와 신중한 판단이 요구된다는 사실을 항상 염두에 두어야 한다. 본 연구에서 제시한 시간분포 방법에 대한 내용은 강우특성 분석 위주로 도출된 결과로, 각각의 시간분포 방법에 대한 보다 정밀한 평가를 위해서는 추가 연구를 통해 유출해석에 의한 민감도분석이 수반되어야 한다.
Fig. 1.
The Ratio of the Maximum Continuous Rainfall for 3-hour to the to Total Rainfall According to Average Rainfall Events Classified by Duration
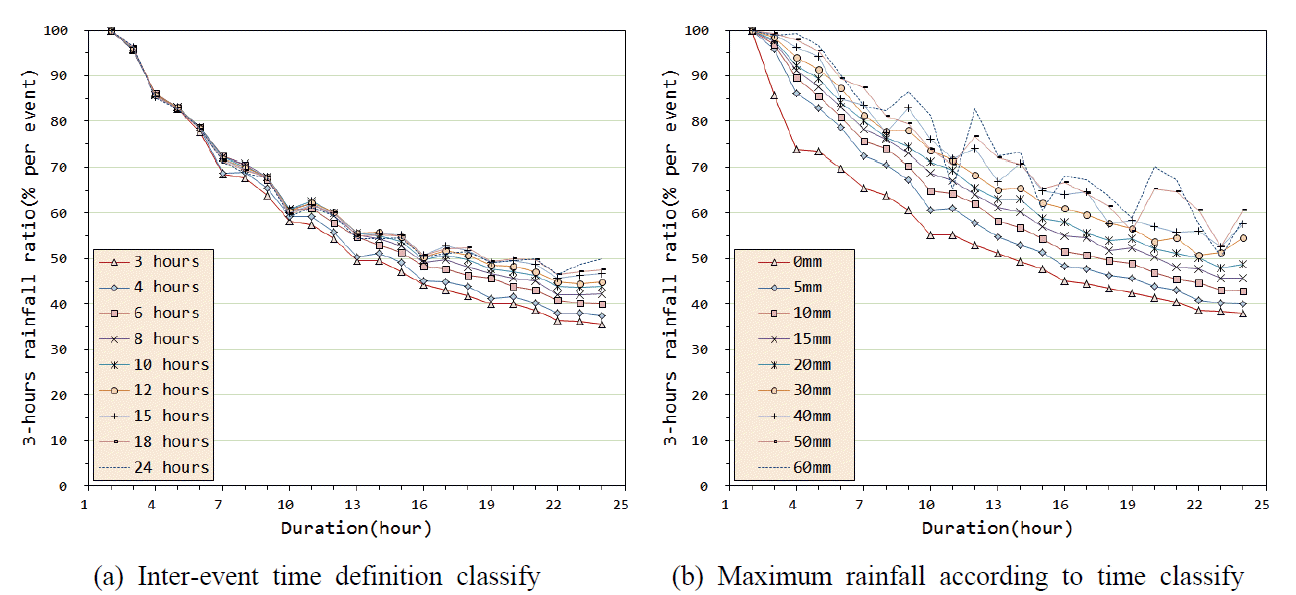
Fig. 2.
Distribution Where the Maximum Rainfall According to Average Rainfall Events Classified by Duration Occurs in Accordance with Inter-event Time Definition
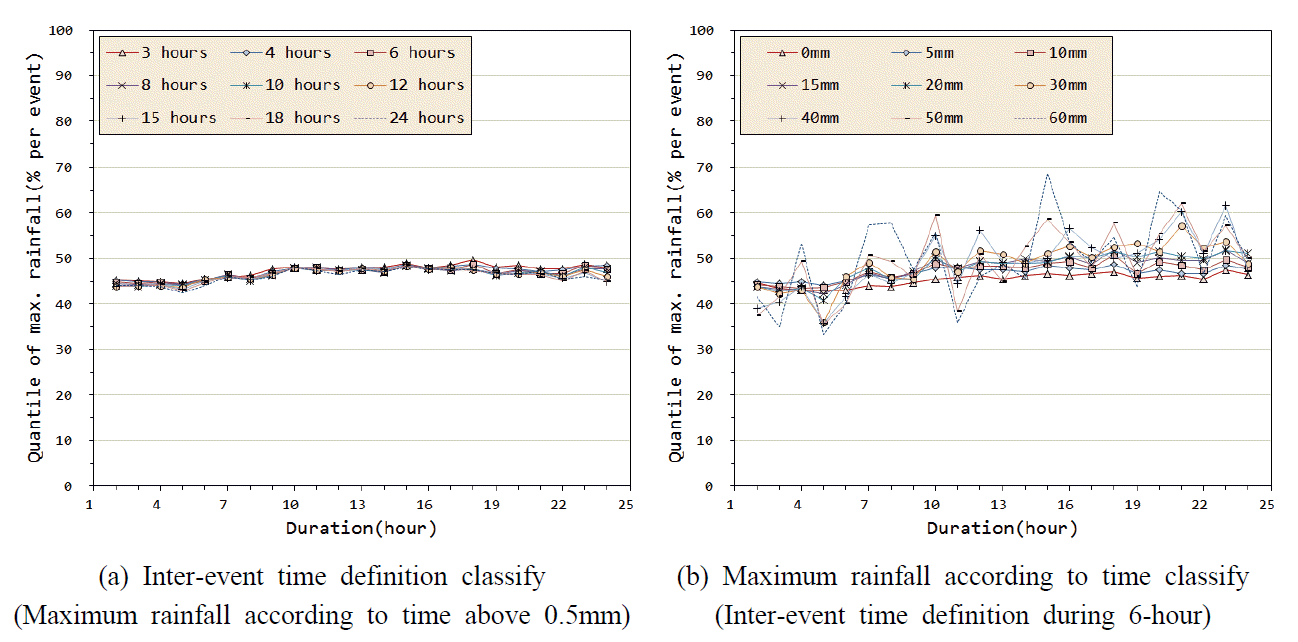
Fig. 3.
The Ratio of the Rainfall Immediately Before to the Maximum Rainfall According to the Average Rainfall Events Classified by Duration
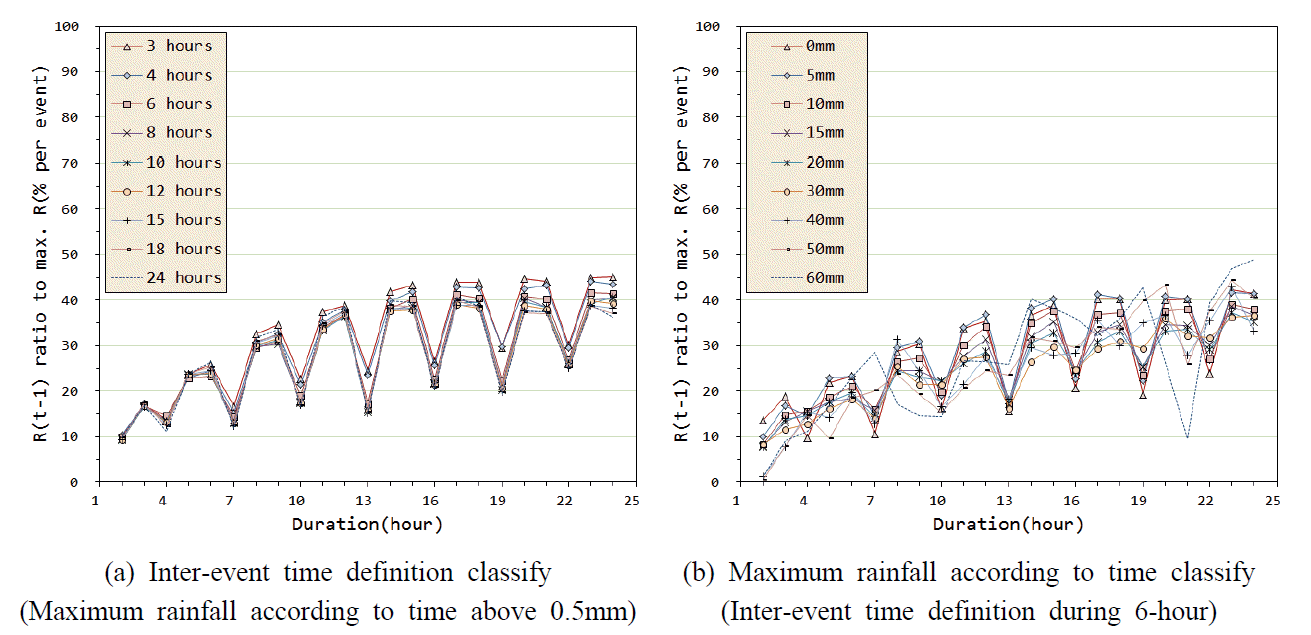
Fig. 4.
The Ratio of the Rainfall Immediately After to the Maximum Rainfall According to the Average Rainfall Events Classified by Duration
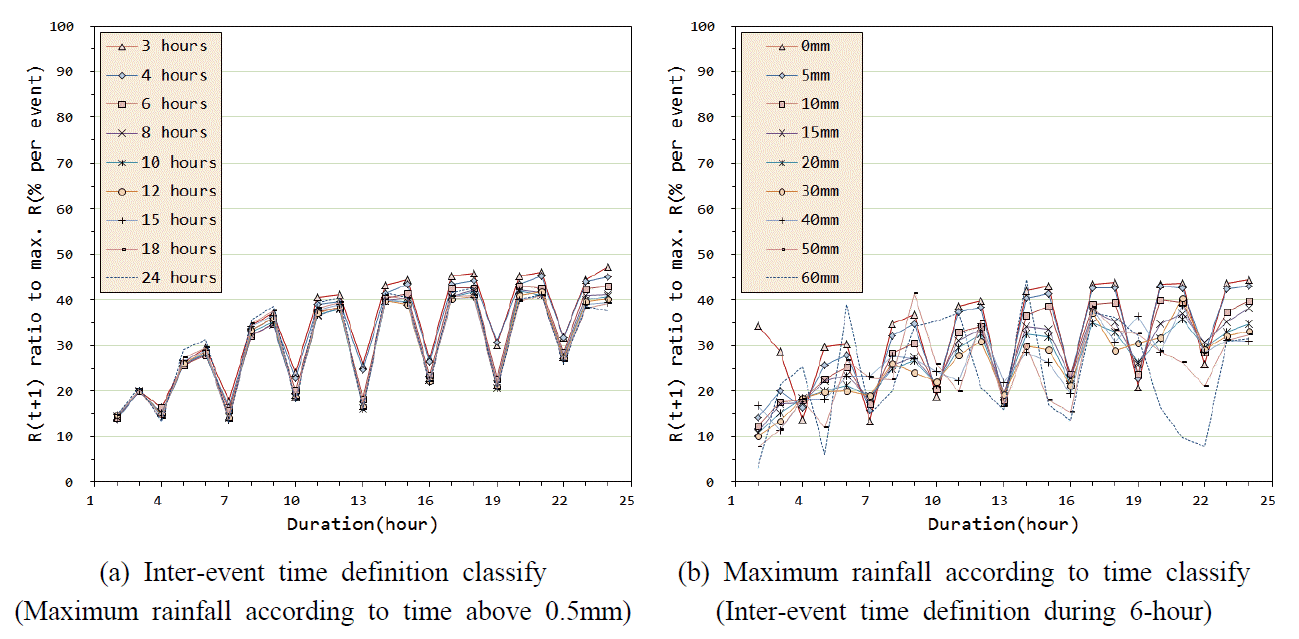
Fig. 5.
The Ratio of the Maximum Rainfall to the Total Rainfall According to the Average Rainfall Events Classified by Duration in Accordance with Maximum Rainfall According to Time
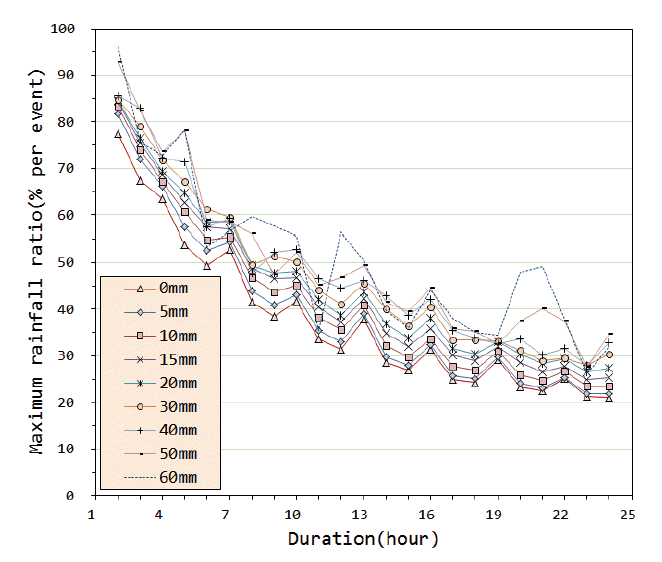
Fig. 8.
Comparison of Actual Distribution and Ideal Distribution for 24-hour (i: incremantal, c: cumulative)
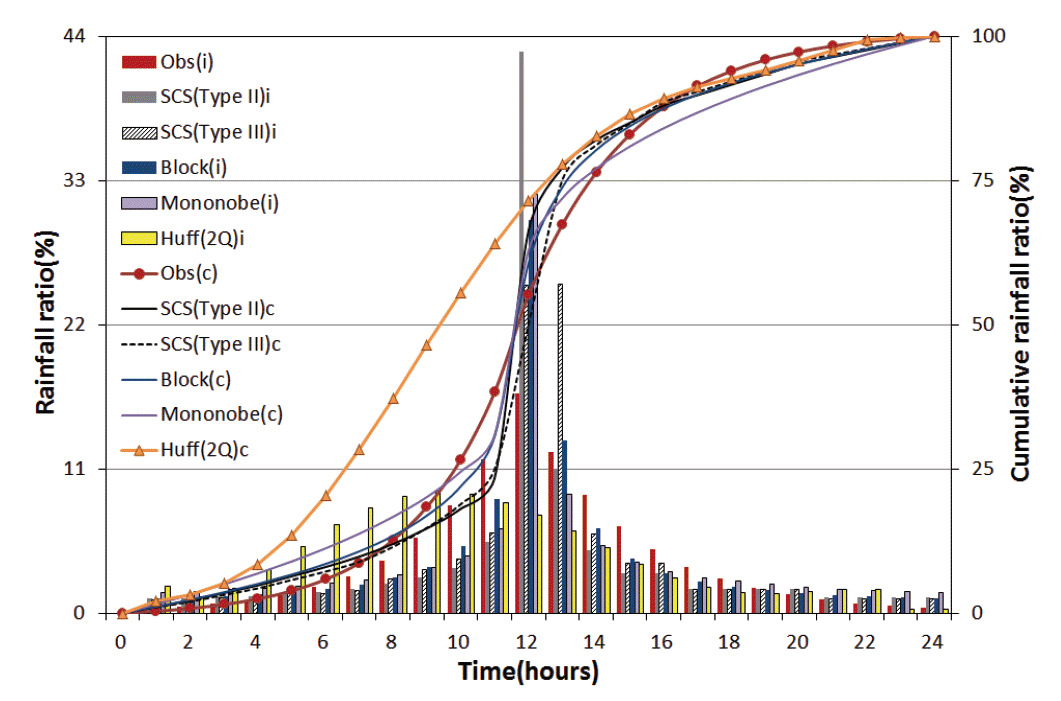
Fig. 10.
Comparison of Actual Distribution, Ideal Distribution and Actual Event for 12-hour During 2010, 2011 Years (after adjustment)
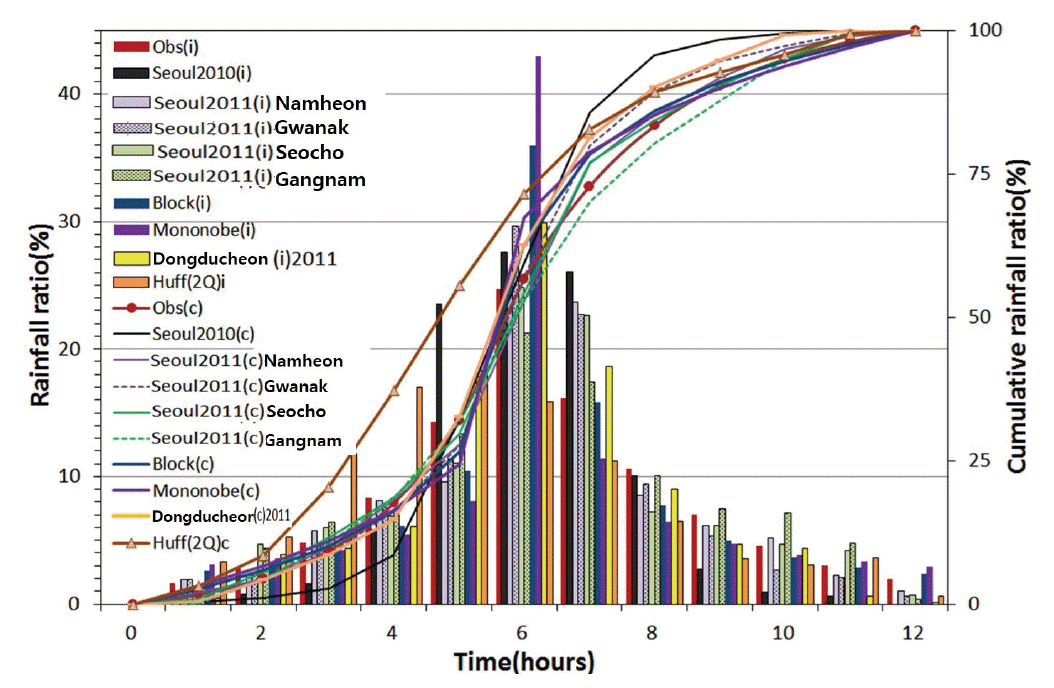
Fig. 11.
Comparison of Actual Distribution, Ideal Distribution and Actual Event for 12-hour During 2010, 2011 Years of Dongducheon (after adjustment)
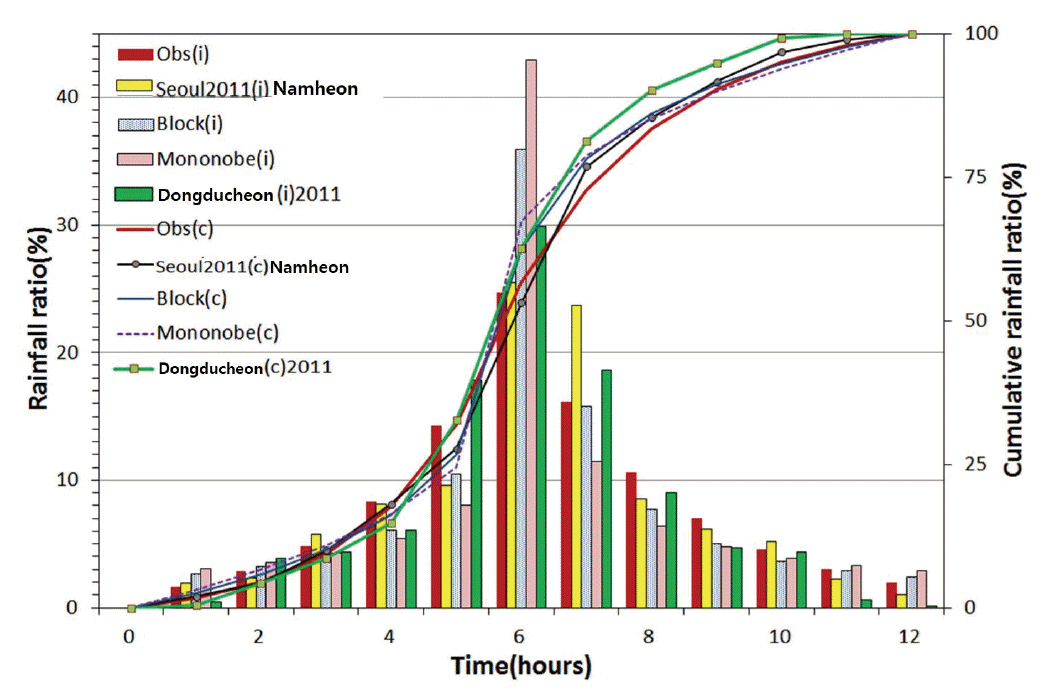
Table 1.
Selected Rainfall for the Time Distribution Analysis in Accordance with Duration
Table 2.
Actual Time Distribution in Accordance with Duration
References
Huff, F.A. (1967) Time Distribution of Rainfall in Heavy Storms. Water Resources Research, Vol. 3, No. 4, pp. 1007-1019.

Huff, F.A. (1986) Urban Hydrology Review. Bulletin of the American Meteorological Society, Vol. 67, No. 6, pp. 703-712.

Huff, F.A. (1990). Time Distribution of Heavy Rainstorms in Illinois. Illinois State Water Survey, Circular No. 173.

Keifer, C.J., and Chu, H.H. (1957) Synthetic Storm Patterns for Drainage Design. Journal of Hydraulics Division, Vol. 83, No. HY4, pp. 1-25.

Lee, K.H. (1983). Studies on the Time Distribution of Heavy Storms. Ph.D. dissertation. Seoul National University.

Ministry of Construction & Transportation (2000). 1999 Report on Water Resources Management Techniques Development: Design Rainfall Temporal Distribution of Regional.

Park, C.Y., Seo, B.H., Yoon, Y.N., and Kang, K.W. (1981) A Study on Rainfall-Pattern Analysis for Determination of Design Flow in Small Watershed. Journal of Korean Association of Hydrological Sciences, Vol. 14, No. 4, pp. 13-18.

Pilgrim, D.H., and Cordery, I. (1975) Rainfall Temporal Patterns for Design Flood. Journal of Hydraulic Division, ASCE. Vol. 101, No. HY1, pp. 81-95.

- TOOLS
-
METRICS

-
- 1 Crossref
- 65,535 View
- 70 Download
- Related articles in KOSHAM