1. 서 론
조인트에서 철근의 부착파괴 및 미끄러짐 변형이 쉽게 발생되는 이유는 다음과 같다. 지진하중에서는 철근의 인장 소성변형에 의하여 인장항복뿐만 아니라 압축항복도 발생한다. 따라서,
Fig. 1과 같이 조인트 좌·우의 보에는 인장항복과 압축항복이 동시에 발생하므로, 원칙적으로는 조인트를 관통하는 보 주근과 콘크리트 사이에는 단순인장 또는 단순압축 응력이 작용하는 경우에 비하여 2배의 부착강도(
T1+
C2 또는
T2+
C1,
Fig. 1 참조)가 필요하다. 하지만 조인트 영역에서 확보할 수 있는 보 주근의 최대 정착길이는 기둥의 단면 깊이인
hc로 제한되므로 충분한 정착성능을 확보하기 어렵다. 철근 직경에 비해 단면 깊이가 작은 경우에는 에너지 소산능력과 강성이 현저히 감소 될 수 있다.
이러한 보-기둥 조인트의 하중전달 특성을 고려하여 KCI 2012, ACI 318-14, NZS 3101:1995 등 국내외의 콘크리트 구조설계기준에서는 내진설계 시 내부 접합부에서 hc/db를 다음과 같이 제한하고 있다.
여기서, αf= 보-기둥 조인트를 관통하는 보 주근의 방향을 고려하는 계수(0.85 ∼ 1.0), α0= 보 소성힌지의 위치를 고려하는 계수(1.0 ∼ 1.25), fck= 콘크리트 설계 압축강도, fy= 철근의 설계 항복응력이다. NZS 3101:1995에서는 ACI 318-08에 비하여 설계조건을 다양하게 고려 가능하다.
이와 같이 접합부의 내진성능을 향상시키기 위해서는 hc/db를 늘려 조인트 영역에서 철근의 정착성능을 향상시켜야 한다. 그러나 현실적으로 hc/db를 늘리는 것은 다음과 같은 제약이 있다. hc/db를 늘리기 위해서는 기둥 치수(hc)를 크게 하거나 철근의 직경(db)을 줄여야 한다. 기둥 치수를 지나치게 크게 할 경우, 건축계획의 제약이 될 뿐만 아니라 건물 내부의 사용 면적이 줄어들어 경제성이 떨어진다. 또한, 철근 직경의 감소는 배근공사의 증가로 이어져 시공성이 나빠질 수 있다.
본 연구에서는 내진성능이 우수하고 기둥 단면크기 제한을 완화할 수 있는 보-기둥 접합부의 조인트 보강 상세를 개발하였다. 보-기둥 조인트에서 철근의 미끄러짐이 발생하는 경우 주기거동 동안 핀칭이 발생하여 에너지 소산능력 및 강성이 감소한다. 개발한 조인트 보강 상세는 보 소성힌지를 조인트 경계로부터 보 경간 내부로 이동시켜 작은 치수의 기둥을 사용하더라도 조인트 영역에서 철근 부착파괴 및 미끄러짐 변형을 줄이도록 고안되었다. 실물 크기의 보-기둥 내부 접합부에 대한 반복재하 실험을 통하여, 개발한 보강 상세의 내진성능 개선 효과를 검증하였다.
2. 조인트 보강 상세
Fig. 2는 RC 보-기둥 접합부의 조인트 보강 상세 개념을 나타낸다.
Figs. 2(a)와
(b)는 각각 조인트를 관통하는 45° 굽힘철근(bent bar)과 90° 갈고리철근(hooked bar)을 보 단면의 상·하부에 추가로 배근하여 조인트를 보강하는 방법이다. 조인트 경계에서는 굽힘철근 및 갈고리철근으로 인하여 보 단면의 휨강도(capacity,
Figs. 2(a)와
(b)의 점선)가 증가한다. 따라서 보 소성힌지의 위험단면은
Fig. 2(a)와 같이 45° 굽힘철근이 교차하거나 또는
Fig. 2(b)와 같이 90° 갈고리철근이 설치되는 보 경간 내부로 이동한다. 조인트 영역에 배치된 굽힘철근 및 갈고리철근으로 인하여, 위험단면에서 시작되는 보 주근의 인장항복은 이후 조인트가 아닌 보 경간의 내부로 확산된다.
이와 같이 보 주근의 항복이 조인트 경계 및 내부로 확산되지 않도록 하기 위해서는, 다음 조건을 만족하도록 45° 굽힘철근 및 90° 갈고리철근의 단면적을 결정하여야 한다(
Fig. 2 참조). 즉, 조인트의 휨모멘트 강도가 소성힌지의 휨강도에 의해 발생하는 조인트의 요구 휨모멘트보다 커야 한다.
여기서
Mn,
Mnj= 보강근(굽힘철근 및 갈고리철근)으로 조인트를 보강하기 전과 후의 보 단면 휨강도,
ls= 기둥면으로부터 보의 휨모멘트가 0이 되는 위치까지의 거리,
dj= 조인트 경계의 기둥면으로부터 보 경간 내부의 위험단면까지의 거리이다.
Eq. (2)와
Fig. 2(b)에서 보의 상부근이 인장을 받는 경우는
Mn'',
Mns',
ls', 등을 사용하여 나타냈다. 철근은 변형경화 거동에 의하여 항복강도의 1.25배까지 응력이 증가하므로,
Eq. (2)로부터 결정되는 45° 굽힘철근 및 90° 갈고리철근의 단면적은 보 주근 단면적의 25% 이상 배치하는 것이 바람직하다(
Korean Concrete Institute, 2012; ACI 318-14). 또한
Figs. 2(a) 및
(b)의 조인트 보강 상세를 적용할 경우 보-기둥 조인트에는 소성힌지의 휨모멘트 강도에 의해 요구되는 설계 전단력으로 설계해야 한다.
조인트 보강 상세를 사용하면 보 소성힌지 위험단면이 조인트 경계의 기둥면으로부터 이격되므로, 조인트를 관통하는 보 주근의 정착길이가 기둥의 단면깊이
hc에서 조인트 보강영역의 깊이
hj(= 조인트 보강근이 45° 또는 90°로 구부려지는 지점 사이의 거리)로 증가한다(
Fig. 2 참조). 따라서 조인트에서 철근과 콘크리트 사이의 정착성능이 개선되고 철근의 미끄러짐 변형을 줄여, 접합부의 내진성능 향상을 기대할 수 있다. 또한 45° 굽힘철근 및 90° 갈고리철근의 절곡위치를 조절하여 보 소성힌지의 위치(
dj 및
dj')를 결정하므로 건축계획적으로 기둥의 단면깊이
hc가 작더라도 조인트 영역에서 보 주근의 정착길이
hj를 충분히 확보할 수 있다.
Fig. 2의 45° 굽힘철근 및 90° 갈고리철근은 일반 철근을 구부려 손쉽게 배근할 수 있으므로, 비용이 저렴하고 시공성 또한 우수하다.
3. 실험 계획
3.1 실험체 상세
보-기둥 접합부 십자형 실험체 S1 ∼ S6을 실물 크기로 제작하여 반복재하 실험을 수행하였다. 실험체는 강기둥-약보 거동을 보이도록 설계되었고, 보 및 기둥의 상세는 KCI 2012 및 ACI 318-14, ACI 352R-02의 특수모멘트골조의 규정을 따랐다. 각 접합부 실험체의 보와 기둥 단면 크기와 배근 상세는
Table 1과
Fig. 3에 나타냈다.
Fig. 3(a)는 조인트를 보강하지 않은 일반 접합부 실험체 S1의 치수 및 배근상세를 보여준다. 기둥 상⋅하 지점간 거리와 보 좌⋅우 지점간 거리가 각각
h= 2100 mm 및
l= 5760 mm이고, 기둥과 보 단면의 크기는 각각 460 mm × 500 mm, 500 mm × 350 mm이다. 보 단면에는 상⋅하 주근으로 각각 4D25(
ρt= 0.013) 및 2D25(
ρb= 0.0065) 철근이 배근되었고, 보 소성힌지 영역에는 후프형 스트럽을 100 mm(<
d/4,
d= 447 mm) 간격으로 사용되었다(
ρv= 0.0041). 기둥 단면에는 주근으로 12D25(
ρ= 0.0266)가 사용되었고, 후프형 띠철근으로 2D13@100(
ρh= 0.0103)가 사용되었다. S1의
hc/
db=18.1로서 KCI 특수모멘트골조 기준(
Eq. (1a))을 만족시키지 못한다.
실험체 S2는
Fig. 3(b)에 나타낸 바와 같이 45° 굽힘철근(3D25)을 사용하여 조인트를 보강하였다. 기둥의 단면 치수와 배근 상세는 S1과 동일하다. 보의 경우 S1과 동일한 단면 치수를 사용하였지만, 굽힘철근에 의한 보 휨강도 증가를 고려하여 상부근을 3D25(
ρt= 0.0098)로 줄였다. 굽힘 보강철근은 기둥면으로부터 101 mm 위치에서 45°로 굽혀 보 단면의 휨강도가 완만하게 줄어들도록 하였고, 인장에 대한 정착길이(1070 mm)를 확보하였다(
Fig. 3(b) 참조).
Fig. 2(a)에 나타낸 바와 같이 보 위험단면의 위치는 상⋅하 굽힘철근이 서로 만나는 지점으로 기둥면으로부터
dj=
dj'= 301 mm 떨어져 있다(
hj= 662 mm). 보 위험단면 부근에는 S1과 동일한 100 mm 간격으로 후프형 스터럽을 배치하였다.
hc/
db=18.1로 동일하지만, 소성힌지가 보쪽으로 이동하여
hj/
db=26.1로 증가하여
Eq. (1a)를 만족한다.
Fig. 3(c)는 3-D25 90° 갈고리철근(3D25)을 사용하여 조인트를 보강한 S3의 배근상세를 보여준다. 기둥과 보의 단면 치수와 배근상세는 S1과 동일하다. 보 단면의 상부와 하부에 배치한 갈고리철근은 조인트 경계로부터 각각 176 및 426 mm 위치에서 굽혀, 정⋅부방향 반복재하 동안 한 곳에 소성변형이 집중되는 것을 완화시켰다(
dj= 426 mm,
hj'= 176 mm,
hj= 812 mm,
Fig. 2(b) 참조). 갈고리철근에 의한 조인트 보강으로 인하여 보에 소성변형이 집중되고 갈고리 정착에 의하여 손상이 발생할 수 있으므로, 보 위험단면 부근에는 후프형 스터럽을 50 mm 간격으로 조밀하게 배치하였다. 예상 소성힌지의 위치를 고려하여
hj/
db= 32.0으로 증가되었다.
Fig. 3(d)는 90° 갈고리철근(3D25)을 사용하여 조인트를 보강한 S4의 배근상세를 보여준다. 보 및 기둥의 단면 치수와 배근 상세는 S1 및 S3과 동일하다. 다만, 갈고리철근 보강에 따른 보 위험단면의 위치가
dj= 231 mm 및
dj'= 106 mm로서, 갈고리철근을 최대한 보-기둥 조인트 경계에 가깝게 배치시켰다. 따라서 S4의 경우 조인트 영역을 관통하는 보 상부근의 정착길이는
hj= 672 mm로서, S3의 정착길이(
hj= 812 mm)보다 작다.
hj/
db는 S3보다 작은 26.5이다.
Fig. 3(e)는 45° 굽힘철근으로 조인트를 보강한 S5 실험체의 배근상세를 보여준다. 이 실험체는 매우 작은 춤의 기둥에 대해 제안된 보강방법의 성능을 검증하고자 제작되었다. 보의 단면 치수, 주근 및 스터럽 배치, 굽힘철근 배치는 S2와 동일하다. 보 위험단면의 위치는 기둥면으로부터
dj=
dj'= 301 mm 떨어져 있다. 다만, 기둥 단면 춤이 작은 360 mm × 710 mm를 사용하여 조인트 영역의 깊이를
hc= 360 mm로 감소시켰다. 따라서 조인트를 관통하는 보 상부근의 정착길이는
hj= 562 mm로서 S2의 정착길이보다 작다.
hc/
db=14.2로서 매우 작으며,
hj/
db=22.1이다.
3.2 실험체 설계 검토
Table 1은 재료실험 결과를 보여주는데, 콘크리트 압축강도는
fck= 29.4 ∼ 46.5 MPa이고, D10, D13, D25(A, for S1 and S3), D25(B, for S2, S4, and S5) 철근의 항복강도는 각각
fy= 462, 496, 452, 475 MPa이다. 계측된 재료강도를 바탕으로 KCI 2012 및 ACI 318-14에 따라 보-기둥 접합부의 내진설계 결과를 검토하여
Table 1에 나타냈다. 주요 결과는 다음과 같다.
(1) Eq. (1a)에서 같이 조인트 영역의 hc/db는 20 이상이어야 한다. Table 1에 나타낸 바와 같이 모든 접합부 실험체는 hc/db는 20보다 작으므로, 설계기준을 만족하지 못한다. 하지만 S2, S3, S4, S5 실험체는 조인트 보강으로 인하여 보의 위험단면이 조인트 경계로부터 멀리 위치하므로, 조인트 좌⋅우의 보 보강근 굽힘 사이의 거리로부터 계산되는 hj/db는 20 이상이 되도록 설계하였다(Table 1 참조).
(2) 조인트를 보강한 S2 ∼ S5 실험체는 Eq. (2)를 만족하도록 설계되었다(Table 1 참조). 따라서 보 주근의 항복은 조인트 경계로부터 dj또는 dj'만큼 떨어진 위험단면 위치에서 발생하도록 제작되었다.
(3) 보-기둥 접합부에서 취성적인 조인트 전단파괴를 방지하기 위해서는, 조인트의 전단 저항성능 Vjn이 요구강도 Vju보다 커야 한다(Korean Concrete Institute, 2012; ACI 318-14). Table 1은 각 접합부 실험체의 Vjn과 Vju을 보여준다. 계산 방법은 Table 1의 주석으로 나타냈다. S1, S3, S4는 를 만족하도록 설계된 반면, S2, S5의 경우 Vjn/Vju가 각각 0.94, 0.97로서 의도적으로 설계기준을 만족하지 못하도록 설계하였다. S2와 S5의 기둥은 단면 형상이 다르지만 단면적이 비슷하므로, S2와 S5의 공칭 조인트 전단저항성능 Vjn은 거의 동일하다(Table 1 참조).
(4) Table 1은 각 접합부 실험체에서 보와 기둥의 휨강도비 ∑Mnc/∑Mnb를 보여준다. 조인트를 보강한 S2 ∼ S5 실험체의 경우 보의 휨항복이 조인트 경계면으로부터 dj또는 dj'떨어진 위치에 발생되므로, 보정된 조인트 경계면의 보 휨강도를 사용하여 ∑Mnc/∑Mnb를 계산하였다. Table 1에 나타낸 바와 같이 모든 실험체는 설계기준에서 제안하는 ∑Mnc/∑Mnb≥1.2를 만족하였다.
3.3 가력 및 계측계획
Fig. 4는 접합부 실험체의 설치 상태를 나타낸다. 보 지지점 사이의 순경간은
l= 5760 mm이고, 기둥 지지점 사이의 높이는
h= 2100 mm이다. 기둥 하부는 회전단이고, 보 양끝은 좌우의 횡방향 변위가 가능하도록 이동단으로 지지되었다. 비틀림을 방지하기 위하여 조인트 좌⋅우측의 보를 횡방향으로 지지하였다. 횡하중은 기둥 상부에서 최대 용량 2000kN, 최대 스트로크 250 mm인 가력기를 사용하여 반복가력을 하였다. ACI 374-05에서 제시하는 방법에 따라 층간변위비 0.25%에서 3번 반복가력 후에 층간변위비를 이전 층간변위비의 1.25∼1.50배 증가시키면서 3번씩 반복가력을 하였다. 실험 시 기둥에는 압축력을 재하하지 않았다.
Fig. 4에 나타난 바와 같이 선형 변위계측기를 사용하여 조인트 전단변형, 기둥 단부의 횡변형, 지점 미끄러짐 변형 등을 계측하였다.
4. 실험 결과
4.1 하중-변위 관계 및 파괴 특성
Fig. 5는 각 접합부 실험체의 횡하중-층간변위비 관계의 주기곡선과 포락곡선을 보여주고,
Fig. 6은 실험이 종료된 이후의 균열 및 파괴 양상을 보여준다. 그림에 나타난 바와 같이 조인트 보강 상세에 따라 각 접합부 실험체는 서로 다른 주기거동 특성 및 파괴 양상을 나타냈다. 조인트를 보강하지 않은 S1의 경우, 조인트 영역에서 보 주근의 부착파괴 및 미끄러짐 변형이 크게 발생되고 콘크리트에는 대각균열이 크게 관찰되었다(
Fig. 6(a)). 반복재하 동안 보 주근의 미끄러짐 변형이 조인트 경계면에 누적되어 조인트와 보 사이의 틈이 점진적으로 커졌다. S1은 조인트 경계면에서 틈의 반복적인 열림-닫힘 작용에 의하여 주기거동 내내 핀칭을 보였고(
Fig. 5(a)), 6.2 %의 변위비에서 조인트 경계면에서 보와 기둥 단부 콘크리트가 파괴되며 접합부가 파괴되었다(
Fig. 6(a) 참조).
Figs. 5(b)와
6(b)는 45° 굽힘철근을 사용하여 조인트를 보강한 S2 실험체의 주기거동 및 파괴특성을 보여준다. 설계의도와 동일하게 4.6 %의 변위비에서 예측된 보 위험단면의 위치(굽힘근이 교차하는 지점)에서 보 콘크리트의 압괴에 의하여 파괴되었지만, 보-기둥 조인트 영역에서도 큰 콘크리트 대각균열이 관찰되었다(
Fig. 6(b) 참조). 이러한 조인트 콘크리트의 대각균열은 철근의 항복침투(yield penetration) 및 소성변형과 관계된 것으로 5장에 자세하게 기술하였다.
Fig. 5(b)에 나타난 바와 같이 S2는 조인트를 보강하지 않은 S1에 비하여 핀칭이 감소된 주기곡선을 보였다. 이러한 접합부의 거동은 기둥 단면의 크기를 줄인 S5 실험체에서도 거의 동일하게 나타났다(
Figs. 5(e) 및
6(e) 참조).
Figs. 5(c)와
(d)는 조인트를 90° 갈고리철근으로 보강한 S3 및 S4의 주기곡선을 보여준다. 두 실험체 모두 조인트를 보강하지 않은 S1에 비하여 핀칭이 크게 감소하고 주기 당 에너지 소산량이 높은 이력거동을 나타냈다.
Fig. 6(c)는 S3의 파괴특성을 보여주는데, 설계의도에 따라 대부분의 소성변형이 갈고리철근이 종료되는 지점의 보 소성힌지에 집중되었고, 결국 4.8%의 변위비에 보 소성힌지의 콘크리트 압괴와 저주파 피로(low-cycle fatigue)에 의한 철근 인장파단으로 파괴되었다. 조인트 영역에서는 주기거동 내내 보 주근의 부착파괴 및 미끄러짐 변형이 거의 없었고 미세한 콘크리트 대각균열만 관찰되었다(
Fig. 6(c) 참조). 이러한 주기거동 및 파괴특성은 갈고리철근이 조인트 경계에 더 가깝게 설치된 S4에서도 거의 동일하게 나타났다(
Figs. 5(d) 및
6(d) 참조).
4.2 하중재하능력, 항복강성, 변형능력
Fig. 6(f)는 각 실험체의 포락곡선을 보여주는데, 이로부터 구한 각 실험체의 최대강도
Pu, 항복변위비
δy, 최대변위비
δu, 연성도
μ(=
δu/
δy), 파괴모드 등을 정리하여
Table 2에 나타냈다.
Fig. 7은 항복변위비
δy의 정의를 보여주는데, 포락곡선을 사용하여 최대강도의 75%를 지나는 할선강성이 최대강도에 도달할 때의 변위비로 정의하였다(
Park, 1988). 최대변위비
δu는 최대강도의 75 %까지 하중재하능력이 저하된 변위비로 정의하였다(
Park, 1988).
Fig. 7은 보-기둥 접합부 실험체의 하중재하능력을 계산하는 방법을 보여준다. 그림에 나타난 바와 같이 보의 위험단면(기둥 경계면으로부터
dj및
dj' 떨어진 지점)에서 단면해석으로 구한 극한휨강도를 사용하여 접합부의 하중재하능력
Pn을 다음과 같이 계산하였다.
여기서,
Mn및
Mn'= 각각 보 위험단면에서 정⋅부방향의 휨강도(
Table 1 참조),
ls및
ls'= 보의 순 경간(clear span,
Table 1 참조),
l= 보 양단부 이동단 사이의 길이,
h= 기둥 상⋅하 힌지 사이의 높이이다.
Table 2는
Eq. (3)으로부터 계산되는 보-기둥 접합부의 하중재하능력
Pn과 실험으로부터 구한 최대강도
Pu를 비교하여 보여준다. 실험에 의한
Pu는 예측된
Pn의 1.01 ∼ 1.12배로서, 모든 실험체에서 접합부의 하중재하능력을 잘 예측하였다.
Table 2는 각 실험체의 항복변위비
δy와 항복강성
ky(=
Pu/
∆y)을 보여준다. 조인트를 보강하지 않은 S1과 90° 갈고리철근을 사용한 S3 및 S4 실험체의 경우, 항복변위비 및 항복강성이 거의 동일하게 평가되었다. 반면 45° 굽힘철근으로 보강한 S2 및 S5 접합부의 경우
Fig. 6(f)의 포락곡선에 나타난 초기거동은 다른 실험체와 거의 동일하였음에도 불구하고, 굽힘철근으로 인하여 접합부 하중재하능력이 증가하므로 상대적으로 항복변위비가 커지고 항복강성은 작게 평가되었다.
Table 2에 나타난 바와 같이 조인트를 보강한 접합부 실험체 S2, S3, S4, S5는 최대 층간변위비가
δu= 4.57∼4.83%로 거의 동일한 수준으로 평가되었다. 다만, S2와 S5의 경우 상대적으로 큰 항복변위비로 인하여, 변위연성도
μ(=
δu/
δy)는 큰 차이를 보였다. 반면, 조인트를 보강하지 않은 S1은
δu= 6.20 (
μ= 4.88)의 우수한 변형능력을 보였다. 보강근을 사용하지 않은 실험체 S1의 우수한 변형능력은 철근의 부착파괴로 인하여 조인트 전체 영역에서 철근의 소성변형이 발생되었고, 그 결과 변형요구량이 조인트 영역에 고르게 분포되었기 때문으로 판단된다. 이와 달리 조인트를 보강한 실험체의 경우 접합부의 변형요구량이 보의 소성힌지에 집중되어 S1 대비 작은 변형능력을 보인 것으로 판단된다. S3과 S4는 보 위험단면에서 후프형 스터럽을 50 mm 간격으로 조밀하게 배근하여 콘크리트 탈락을 최대한 지연시켰다. 그 결과
Fig. 5에 나타난 바와 같이 주기거동에 의한 강도 및 강성 저하가 S2 및 S5에 비하여 감소되었다. 그러나 50 mm 간격의 후프형 스터럽 배치에도 불구하고, S3 및 S4 실험체는 결국 약 4.7% 변위비에서 보 단부 피복콘크리트 파괴와 반복거동에 의한 하부근의 좌굴 및 인장파단이 순차적으로 발생되며 파괴되었다.
4.3 에너지 소산 능력
Fig. 8은 각 접합부 실험체의 에너지 소산능력을 비교하여 보여준다.
Fig. 8(a)는 해당 층간변위비까지 누적된 총 에너지 소산량을 보여주고,
Fig. 8(b)는 층간변위비마다 주기 당 에너지 소산비율
κ를 보여준다. 주기 당 에너지 소산비율
κ는 한 주기 동안 소산하는 에너지량 (주기곡선으로 둘러싸인 면적)을 탄소성 거동에 의한 평행사변형 면적
Eep으로 나눈 값으로 정의된다(
κ=
ED/
Eep,
Fig. 8(b) 참조).
κ는 동일한 층간변위비에서 반복되는 세 번째 주기거동에 대하여 계산하였다.
층간변위비가 거의 동일한 경우, 조인트 영역에서 철근 부착파괴 및 미끄러짐 변형이 크게 발생된 S1은 주기거동 동안 핀칭이 크게 발생하여 누적 및 주기 당 에너지 소산량이 가장 적었다. 반면 조인트를 보강한 S2 ∼ S5 실험체들의 경우 핀칭이 감소하여 개선된 에너지 소산능력을 나타냈다. 특히 90° 갈고리철근으로 보강한 S3 및 S4 실험체는 가장 우수한 주기 당 에너지 소산능력을 보였다.
Fig. 8(b)에 나타낸 주기 당 에너지 소산비율
κ는 조인트 영역의 정착길이
hc또는
hj와 비례적인 관계를 갖는 것으로 나타났는데,
hc/
db 또는
hj/
db가 클수록 더 높은 에너지 소산비율
κ이 증가하였다. 예를 들어, 90° 갈고리철근으로 보강된 S3 및 S4 실험체는 각각
hj/
db= 32.0 및 26.5 (
Table 1 참조)로서, 조인트 영역의 정착길이가 큰 S3의 에너지 소산비율이 S4보다 높았다. S1 실험체는
hc/
db= 18.1로서 가장 작은 에너지 소산비율을 보였다.
ACI 374-05에서는 내진 접합부의 최소 요건으로 층간변위비 3.5%에서 에너지 소산비율
κ가 0.125보다 크도록 요구하고 있다.
Fig. 8(b)에 나타낸 바와 같이 모든 접합부 실험체는 ACI 374-05의 에너지 소산 기준을 만족하는 것으로 나타났다. 하지만 조인트 보강 상세에 따라 큰 편차를 보였다. 조인트를 보강하지 않은 S1 실험체의 경우 약
κ= 0.18을 보였고, 반면 90° 갈고리철근으로 조인트를 보강한 S3 및 S4 실험체는
κ=0.3 내외의 높은 에너지 소산비율을 보였다.
4.4 조인트 전단변형
Fig. 9(a)는 조인트 영역에서 전단변형률
ϒj를 계측하는 방법을 보여준다.
ϒj는 조인트 영역에 대각방향으로 설치한 2개의 LVDT 변형 계측값을 이용하여 계산하였다.
Fig. 9(a)는 각 실험체의 층간변위비 증가에 따른 조인트 전단변형률의 변화를 보여준다. S2 실험체는 실험 중 계측장비 이상으로 층간변위비
δ= 1.99 %에서 계측이 중단되었다.
Fig. 6에 나타난 바와 같이 실험 동안 조인트 영역에서 큰 폭의 콘크리트 대각균열이 관찰된 접합부 실험체 S1, S2, S5에서 상대적으로 큰 전단변형이 계측되었다. 반면 조인트 영역에서 미세한 콘크리트 대각균열이 발생된 S3과 S4는 가장 작은 조인트 전단변형을 보였고, 층간변위비가 증가되더라도 조인트 전단변형의 증가폭이 크지 않았다.
Fig. 9(b)는 각 실험체에 대하여 조인트 전단저항성능
Vju/
Vjn에 따른 최대 전단변형률
ϒmax의 관계를 보여준다.
Vju와
Vjn은 실제 재료강도를 사용하여 ACI 352R-02에 제시된 방법으로 계산한 조인트의 요구 전단력과 전단저항이다(
Table 1 참조). S2 실험체의 경우 계측이 중단된
δ= 1.99 %의 전단변형을
ϒmax로 사용하였다. 그림에 나타난 바와 같이 조인트 영역의 전단변형은
Vju/
Vjn와 관계가 없는 것으로 나타났다. 조인트를 보강하지 않은 S1 실험체는 높은 콘크리트 강도로 인하여
Vju/
Vjn이 가장 작아 전단요구 대비 가장 큰 전단저항을 확보하고 있음에도 불구하고, S2, S3, S4, S5 실험체들보다 더 큰 전단변형이 발생되었다. 이러한 결과는 조인트의 전단변형
ϒj가 전단력
Vju에 의하여 결정되지 않았음을 가리킨다.
5. 조인트의 전단변형과 철근 소성변형
Fig. 10은 강기둥-약보로 설계된 보-기둥 접합부에서 항복 이후 조인트에 발생되는 전단변형 메커니즘을 보여준다. 일반적으로 콘크리트 스트럿은 거의 탄성거동을 보이므로 스트럿의 압축변형은 철근의 인장변형에 비하여 무시할 수 있을 정도로 작다. 따라서 조인트에 전단변형
ϒj가 발생되기 전과 후의 대각방향 콘크리트 스트럿의 길이는 거의 같다. 이는 조인트에서 전단변형
ϒj가 발생하기 위해서는
Fig. 10에 나타난 바와 같이 수평방향의 인장변형
eh가 발생되어야 하며,
eh가 커질수록
ϒj도 증가함을 가리킨다.
eh는 조인트를 관통하는 철근의 인장변형에 의하여 발생되므로, 조인트의 전단변형은 조인트 철근의 소성 인장변형과 직접적으로 관계된다.
Fig. 11은 각 접합부 실험체의 조인트 영역에서 계측한 철근의 변형률 분포를 보여준다. 계측된 철근의 변형률은 동일한 층간변위비에서 주기거동이 3회 반복되는 동안 철근이 경험하는 최대 변형률로서, 조인트를 관통하는 보의 하부철근에 설치한 1축 변형률 게이지로 계측하였다. 실험 시 접합부의 변위비가
δ= 3.0 %를 초과하는 경우 대부분의 변형률 게이지에서 전기신호가 끊겼다. 따라서
Fig. 11의 철근 변형률 분포는 약
δ= 2.7 % 변위비까지 나타냈다.
Fig. 9(b)에 나타난 바와 같이 S1을 제외한 조인트를 보강한 모든 접합부는 약
δ= 2.7 % 변위비에서 거의 최대 조인트 전단변형이 발생하였다.
90° 갈고리철근으로 조인트를 보강한 S3 및 S4 실험체의 경우,
Figs. 11(c)와
(d)에 보는 바와 같이 철근의 변형률이 거의 탄성 상태에 존재하였다. 이는 조인트 영역에서 수평방향 인장변형
eh와 전단변형
ϒj가 매우 작았음을 가리킨다(
Fig. 9(a) 참조). 반면 45° 굽힘철근으로 조인트를 보강한 S2 및 S5의 경우(
Figs. 11(b) 및
(e) 참조), 보의 위험단면에서 시작된 철근 인장항복이 조인트 내부로 확산되는 항복침투가 발생하여 조인트 경계 근처에서 최대 0.0048의 변형률이 계측되었다(항복변형률
ϵy=0.0023). 이는 조인트 내부로부터 누적되는 철근의 인장 소성변형으로 인하여 조인트 경계에 틈(조인트의 수평 인장변형
eh)이 발생되고, 그 결과 조인트 영역에서 전단변형
ϒj이 증가되었음을 가리킨다(
Fig. 9(a) 참조).
Fig. 11(a)는 조인트를 보강하지 않은 S1 접합부의 철근 변형률 분포를 보여주는데, 심각한 항복침투로 인하여 조인트 전체 영역에서 철근에 큰 소성변형률이 발생되었고 그 결과 부착파괴에 의한(2.0 및 2.73 % 변위비의 변형률 분포 참조) 조인트 경계에서 큰 미끄러짐 변형(조인트 수평 인장변형
eh)이 관찰되었고,
Fig. 6(a)에 나타난 바와 같이 주기거동 동안 조인트 전단변형에 의한 핀칭이 크게 발생되었다. 조인트의 전단성능과 균열은
Vju/
Vjn보다는 보 철근의 미끄러짐이 더 큰 영향을 미치며, 따라서 조인트의 전단 손상을 억제하기 위해서는 조인트 내에서 보 철근의 항복을 억제해야 한다.
6. 결 론
본 연구에서는 기둥의 단면 춤이 작은 보-기둥 접합부의 내진설계에 사용할 수 있는 45° 굽힘철근 및 90° 갈고리철근을 이용한 조인트 보강방법을 제안하였다. 6개의 실험체에 대하여 주기하중에 대한 실험을 수행하고, 제안된 조인트 보강방법의 효과를 검증하였다. 이 연구의 주요 결과는 다음과 같다.
(1) 90° 갈고리철근 및 45° 굽힘철근을 사용하여 조인트를 보강한 접합부는 보 경간 내부에 소성힌지를 발생시켜 조인트의 변형요구량 집중을 완화시켰다. 그 결과 기둥의 단면 깊이가 설계기준에 제시된 값보다 작음에도 불구하고 우수한 내진성능을 발휘하였다.
(2) 조인트를 보강한 접합부 실험체는 보강근이 끝나는 위치의 보 소성힌지에서 보 하부 피복 콘크리트 파괴와 이어지는 철근의 좌굴로 하중재하능력이 저하되며 파괴되었다. 반면 기존 접합부 실험체는 보-기둥 조인트 영역에서 과도한 부착파괴로 조인트 경계면에서 보와 기둥 단부 콘크리트가 파괴되었다.
(3) 기존 접합부 실험체는 층간변위비 5.98∼6.20%의 변형능력을 보였고, 조인트를 보강한 실험체들은 보 소성힌지에 변형요구량이 집중되므로 4.57∼4.81%의 다소 감소된 변형능력을 보였다. 이러한 접합부의 변형능력은 ACI 374.1-05에서 요구하는 변형능력 3.5%를 크게 상회하는 값이다.
(4) 기존 접합부 실험체는 조인트에서 철근의 부착파괴 및 미끄러짐 변형으로 인하여 핀칭이 큰 주기거동을 보였다. 반면 45° 굽힘철근 및 90° 갈고리철근으로 보강한 접합부 실험체의 경우 핀칭이 감소하여 에너지 소산이 우수한 주기거동을 보였다.
(5) 조인트의 전단변형 및 콘크리트 대각균열은 조인트 영역에서 보 주근의 항복침투와 그로 인한 슬립변형이 더욱 크게 발생하였다. 제안된 보강 상세는 철근의 슬립거동뿐만 아니라 조인트의 전단변형 억제에도 효과적이었다.
감사의 글
이 연구는 행정안전부 재난관리지원기술개발사업(과제번호: 2017-MPSS31-003)의 연구비 지원을 받아 수행되었습니다. 연구비 지원에 감사드립니다.
Fig. 1.
Beam-column Joint Subjected to Earthquake Load

Fig. 2.
Reinforcement Details at Beam-column Joint
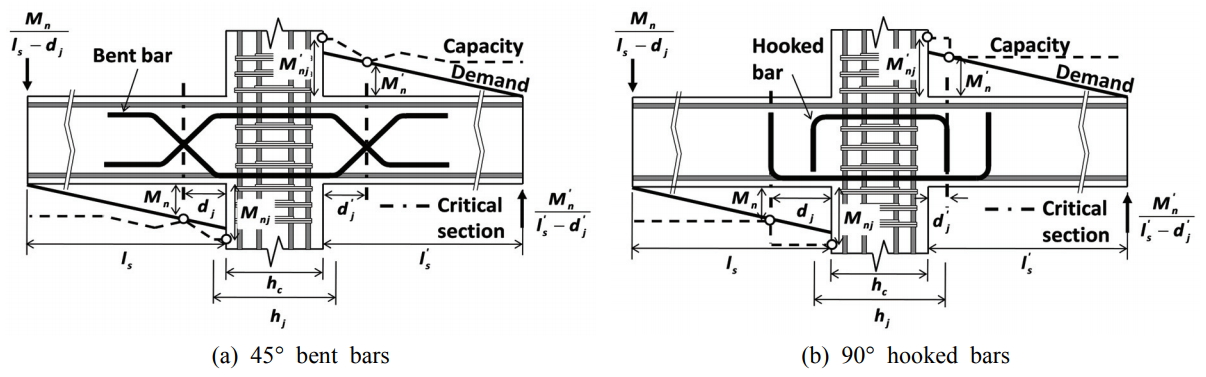
Fig. 3.
Dimensions and Re-bar Details of Test Specimens
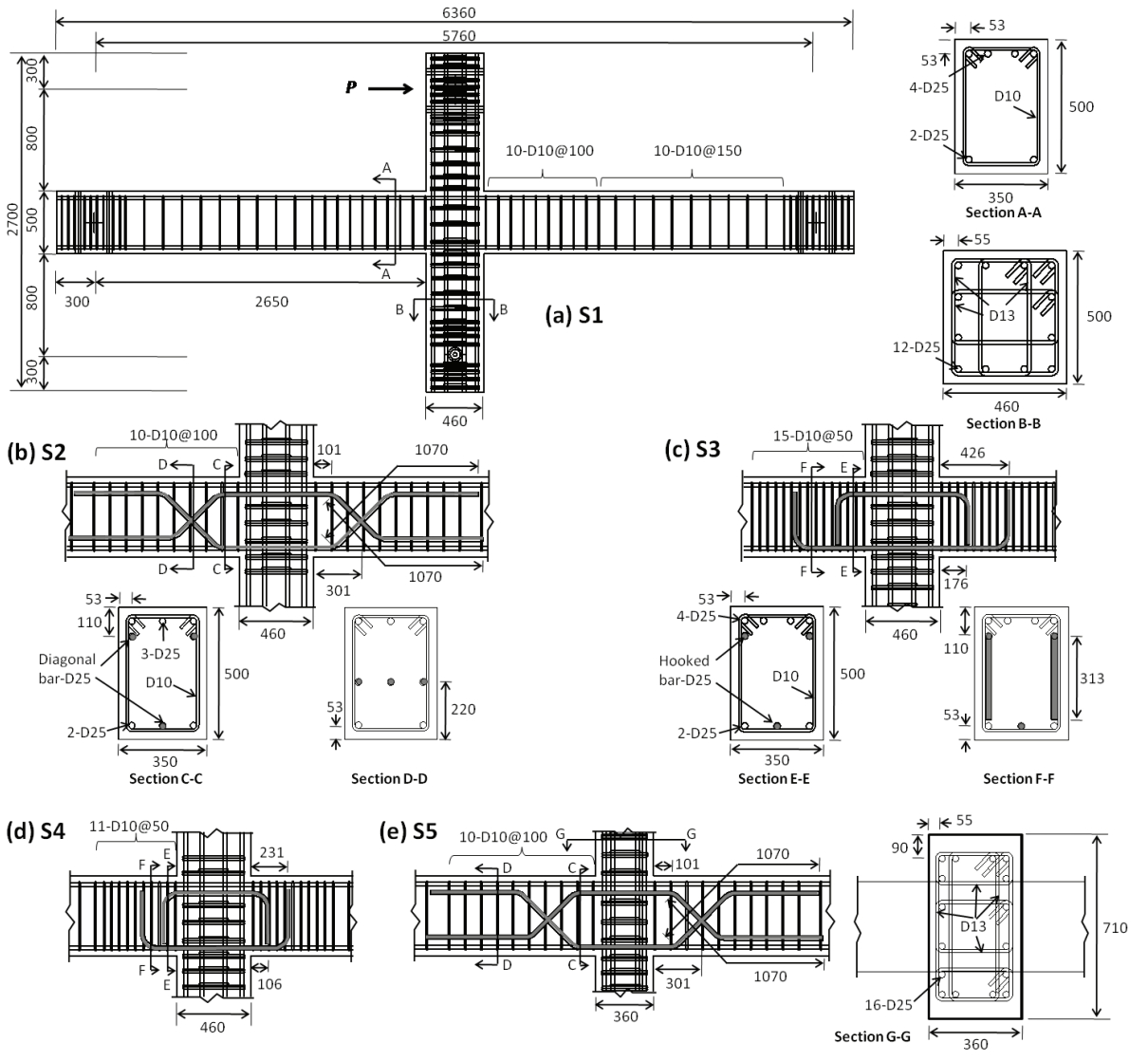
Fig. 4.
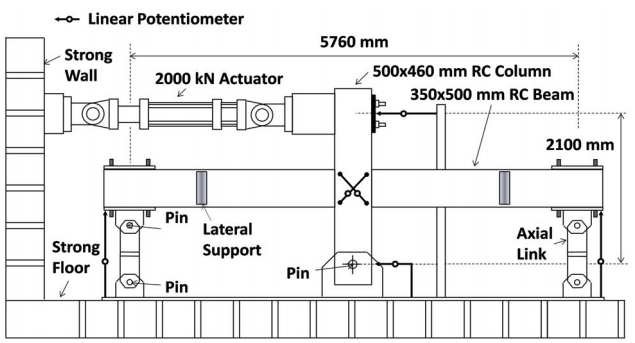
Fig. 5.
Lateral Load - Story Drift Relation of Specimens

Fig. 6.
Failure Modes of Test Specimens at the End of Test

Fig. 7.
Load-carrying Capacity of Connections

Fig. 8.
Energy Dissipation Ratio Per Load Cycle Varying with Story Drift Ratio
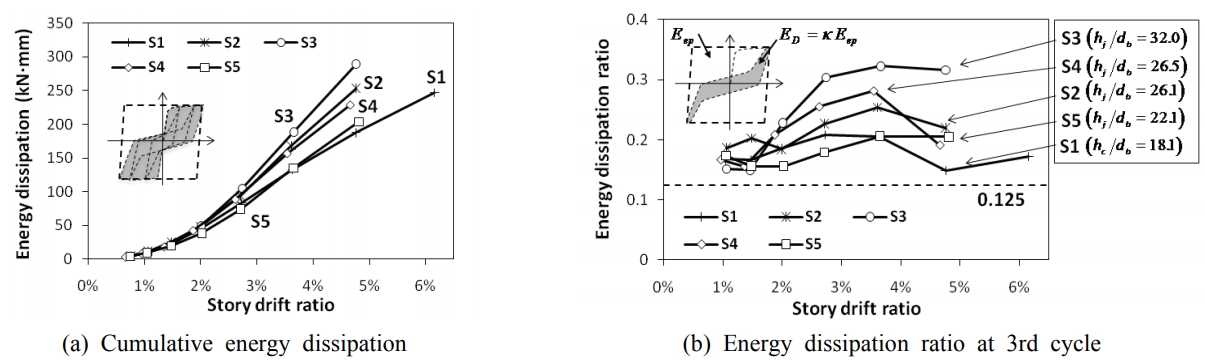
Fig. 9.
Joint Shear Deformation of Connection Specimens
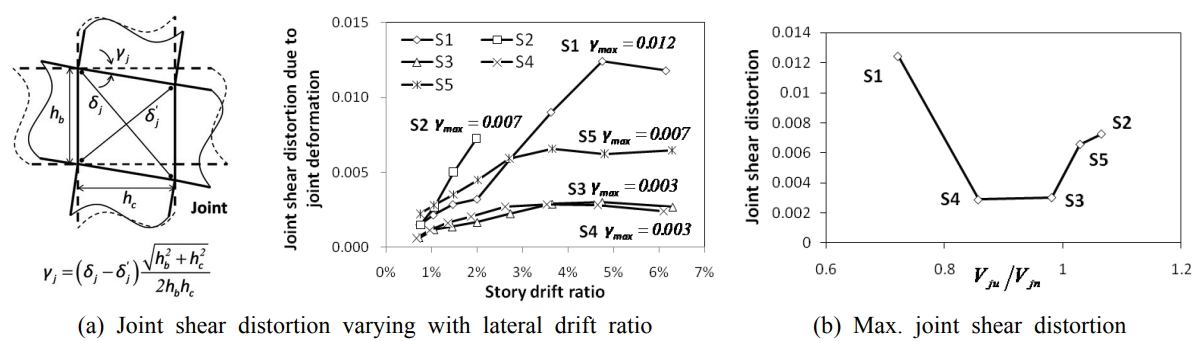
Fig. 10.
Mechanism of Joint Deformation

Fig. 11.
Longitudinal Strain Distribution in Joint

Table 1.
Design Results of Connection Specimens
|
Specimens |
S1 |
S2 |
S3 |
S4 |
S5 |
|
Material strengths |
Concrete strength fck (MPa) |
38.3 |
32.0 |
29.4 |
37.5 |
35.9 |
|
|
Re-bar yield strength fy (MPa)1)
|
462, 496, 452, and 475 MPa for D10, D13, D25(A), and D25(B) |
|
|
Beam |
Dimensions (bb × hb, mm × mm) |
350 × 500 |
350 × 500 |
350 × 500 |
350 × 500 |
350 × 500 |
|
Top re-bars (ρt2), %) |
4-D25 (1.30) |
3-D25 (0.98) |
4-D25 (1.30) |
4-D25 (1.30) |
3-D25 (0.98) |
|
Bottom re-bars (ρb2), %) |
2-D25 (0.65) |
2-D25 (0.65) |
2-D25 (0.65) |
2-D25 (0.65) |
2-D25 (0.65) |
|
Joint-reinforcing details3) (dj and dj´, mm) |
- |
Type 1 |
Type 2 |
Type 2 |
Type 1 |
|
Stirrups at plastic hinge (ρv, %) |
|
(301 / 301) |
(426 / 176) |
(231 / 106) |
(301 / 301) |
|
Moments Mn and Mnj (kN-m)4)
|
D10@100(0.41) |
D10@100(0.41) |
D10@50(0.81) |
D10@50(0.81) |
D10@100(0.41) |
|
Moments Mn´ and Mnj´ (kN-m)4)
|
197 / - |
2499) / 297 |
194 / 282 |
206 / 301 |
2529) / 300 |
|
Mnj/[Mnls/(ls-dj)]5) (Eq. (2)) |
375 / - |
3699) / 437 |
364 / 483 |
391 / 527 |
3779) / 445 |
|
Mnj´/[Mn´ls/(ls-dj´)]5) (Eq. (2)) |
- |
1.06 |
1.22 |
1.33 |
1.06 |
|
- |
1.05 |
1.24 |
1.29 |
1.05 |
|
|
Column |
Dimensions (bc × hc, mm × mm) |
500 × 460 |
500 × 460 |
500 × 460 |
500 × 460 |
710 × 360 |
|
Main re-bar ratio (p, %) |
12-D25 (2.66) |
12-D25 (2.66) |
12-D25 (2.66) |
12-D25 (2.66) |
16-D25 (3.19) |
|
Hoops (ρh, %) |
D13@100(1.03) |
D13@100(1.03) |
D13@100(1.03) |
D13@100(1.03) |
D13@100(1.45) |
|
Moments Mnc (kN-m)4)
|
454 |
442 |
436 |
453 |
459 |
|
Shear demands Vc(kN)6)
|
296 |
361 |
321 |
328 |
367 |
|
|
Joint |
hc/db and hj/db
|
18.1 / - |
18.1 / 26.1 |
18.1 / 32.0 |
18.1 / 26.5 |
14.2 / 22.1 |
|
Joint shear Vju and Vjn (kN)7)
|
1087/1506=0.72 |
1466/1377=1.06 |
1295/1320=0.98 |
1278/1491=0.86 |
1464/1423=1.03 |
|
|
Column-to-beam moment ratio ∑Mnc/∑Mnb8)
|
1.59 |
1.27 |
1.41 |
1.43 |
1.30 |
Table 2.
|
Specimen |
Load-carrying capacity
|
Deformation capacity
|
Stiffness
|
Failure mode |
|
Test |
Prediction |
PuPn
|
Yield drift ratio |
Maximum drift ratio |
Ductility |
ky, kN/mm |
|
Pu, kN |
Pn, kN |
δy, % |
δu, % |
μ=δuδy
|
|
S1 |
310 |
296 |
1.05 |
1.27 |
6.20 |
4.88 |
22.95 |
Joint failure1)
|
|
S2 |
406 |
361 |
1.12 |
1.85 |
4.57 |
2.47 |
19.25 |
Beam failure2)
|
|
S3 |
330 |
321 |
1.03 |
1.22 |
4.83 |
3.98 |
22.83 |
Beam failure2)
|
|
S4 |
332 |
328 |
1.01 |
1.27 |
4.68 |
3.69 |
23.64 |
Beam failure2)
|
|
S5 |
394 |
367 |
1.07 |
1.77 |
4.81 |
2.71 |
20.21 |
Beam failure2)
|
References
ACI 318-14 (2014) Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute.

ACI Committee 374 (2005) Acceptance Criteria for Moment Frames Based on Structural Testing and Commentary. ACI 374.1-05, American Concrete Institute.

ACI-ASCE Committee 352 (2002) Recommendations for Design of Beam-Column Connections in Monolithic Reinforced Concrete Structures. ACI 352R-02, American Concrete Institute.

Brooke, N.J., Megget, L.M., and Ingham, J.M. (2006) Bond Performance of Interior Beam-Column Joints with High-Strength Reinforcement.
ACI Structural Journal, Vol. 103, No. 4, pp. 596-603.

Hakuto, S., Park, R., and Tanaka, H. (1999) Effect of Deterioration of Bond of Beam Bars Passing through Interior Beam-Column Joints of Flexural Strength and Ductility.
ACI Structural Journal, Vol. 96, No. 5, pp. 858-864.

Kitayama, K., Otani, S., and Aoyama, H. (1987) Earthquake Resistant Design Criteria For Reinforced Concrete Interior Beam-Column Joints.
Proceedings of Pacific Conference on Earthquake Engineering, New Zealand, Vol. 1, pp. 315-326.

Korean Concrete Institute (2012) Structural Design Code for Concrete.

Leon, R.T. (1987) Interior Joints with Variable Anchorage Lengths.
Journal of Structural Engineering, ASCE. Vol. 115, No. 9, pp. 2261-2275.

Lin, C.M. (2000). Seismic Behaviour and Design of Reinforced Concrete Interior Beam Column Joints. Department of Civil Engineering, University of Canterbury, Research Report 2000-1, Christchurch, New Zealand.

NZS 3101 (1995) The Design of Concrete Structures. Standards New Zealand, Welington, New Zealand, p. 256.

Park, R. (1988) State-of-the Art Report: Ductility Evaluation from Laboratory and Analytical Testing.
Proceedings of 9th World Conference on Earthquake Engineering, Vol. 8, pp. 605-616.




















