강우 자료의 비정규성이 단순크리깅에 미치는 영향 평가
Evaluation of Rainfall Non-normality on the Simple Kriging
Article information
Abstract
본 연구에서는 정량적 강우장을 추정하는데 있어, 강우 자료의 비정규성이 단순크리깅에 미치는 영향을 평가하였다. 이를 위해 먼저 정규분포를 따르지 않는 두 종류의 자료를 생성하였다. 한 자료는 비정규성이 약하게 나타난 자료이고, 다른 자료는 극단적인 값을 포함하여 비정규성이 강하게 나타난 자료이다. 본 연구에서는 각 자료의 정규성과 비정규성을 가정한 경우에 베리오그램을 유도하였다. 특히, 정규분포를 따르지 않는 자료에 정규성을 가정할 때 베리오그램 유도에 미치는 영향을 평가하였다. 또한 결정된 베리오그램을 이용하여 단순크리깅을 수행한 후 원자료의 분포와 비교하여 자료의 비정규성이 단순크리깅에 미치는 영향을 분석하였다. 마지막으로 관악산 레이더 강우 자료를 이용하여 위 과정을 반복하고 그 결과를 평가하였다. 연구를 통해 얻은 결과를 정리하면 다음과 같다. 첫째, 정규분포를 따르지 않는 자료에 정규성을 가정하여 베리오그램을 유도할 경우 원자료의 특성에 적합한 베리오그램을 결정하기 어려운 것으로 나타났다. 둘 째, 모의자료를 이용한 분석에서는 자료에 극단적인 값이 포함되지 않은 경우 정규성을 가정한 단순크리깅 결과가 양호하게 나타났다. 마지막으로, 레이더 강우 자료를 이용한 분석에서도 위와 유사한 결과를 확인할 수 있었다.
Trans Abstract
This study evaluated the effect of rainfall non-normality on the estimation of quantitative rainfall field by the simple Kriging. For this purpose, two different data fields were generated not to follow the normal distribution. One is to show the weak non-normality, and the other the strong non-normality with extreme values. Variograms were then derived under the assumption of the normality and nonnormality for each data. Here, the effect of assuming normality was also evaluated when deriving the variogram. Variograms were also applied to the two data field generated and evaluated the effect of the data non-normality on the simple Kriging result by comparing it with origin data field. Finally, above procedure was repeated with the real radar data from the Gwanaksan Radar. Summarizing the results are as follows. First, it was not easy to derive the proper variogram for the non-normal data under the assumption of normality. Second, when applying the variogram derived under the assumption of normality, the simple Kriging results was better for the generated data without extreme values. Finally, similar results could also be derived in the application of the real radar data field.
1. 서론
전세계적으로 기후변화에 의한 이상기상 및 이상홍수의 발생이 증가하고 있고 이로 인한 인명 및 재산피해가 증가하고 있다. 지구온난화, 엘리뇨, 라니냐, 슈퍼태풍, 돌발홍수 및 게릴라성 호우 등의 현상이 빈번히 발생하였고, 국내의 경우 지난 30여년 간 하루 평균 80 mm 이상의 강수일수가 50% 증가하였다(NEMA, 2007). 더욱이 한반도의 경우 지리 및 지형학적 특성으로 인하여 장마, 태풍, 대류성 강우 등 집중호우에 의한 돌발홍수 위험에 노출되어 있다. 이러한 문제에 근본적으로 대응하기 위해서는 보다 정밀한 강우관측 기술이 필요하다. 기존에는 우량계를 곳곳에 설치하여 강우 관측을 시도 하였으나 강우의 공간적 변동성을 파악할 수 없고, 설치 및 유지관리가 쉽지 않은 문제가 있었다. 특히, 강우의 변동성이 크게 나타나는 산악지역에서는 관측능력에 큰 한계가 있었다 (MOCT, 2001).
최근에는 기상청, 국토해양부, 공군 등 관련기관에서 레이더를 도입하여 보다 광범위한 강우 관측을 수행하고 있다. 레이더는 시공간적으로 고해상도의 강우 관측을 가능하게 하였으며, 공간적으로 균등하고 시간에 따라 연속적인 자료를 제공한다(MOCT, 2003; 2004; Suk et al., 2005). 그러나 이러한 장점에도 불구하고 레이더 강우는 그 자체가 원격 탐사된 값으로 반드시 참값을 나타내지 못하는 문제가 있다. 이러한 문제를 극복하고 레이더 강우 자료의 활용을 극대화하기 위해 정량적 강수추정(Quantitative Precipitation Estimation)과 관련된 연구가 수행되고 있다. 최근에는 이러한 연구 중 우량계 강우의 장점과 레이더 강우의 장점을 결합하려는 합성과 관련된 연구가 주목받고 있으며, 연속수정법, 가우시안머징, 코크리깅 등의 기법이 합성에 이용되었다(Krajewski, 1987; Seo et al., 1990; Hevesi et al., 1992; Seo and Breidenbach, 2002; Sinclair and Pegram, 2005; Goudenhoofdt and Delobbe, 2009; Seo, 2012; Pettazzi and Salson, 2012, Martens, 2013; Kim et al., 2007; Yoo and Park, 2008; Kim et al., 2008). 여기서 코크리깅은 크리깅의 여러 방법 중 하나이다.
크리깅은 값을 알고 있는 지점의 자료를 가중선형 조합하여 미지점의 값을 예측하는 경험적 방법으로 지구통계학 분야에서 사용되는 보간 기법이다. 1950년대 남아프리카공화국의 채광공학자 Krige는 광맥의 분포를 파악하기 위한 경험적 방법을 소개하였고, 이는 프랑스의 지질수학자 Matheron에 의해 정립되면서 크리깅이라 불리어졌다(Cressie, 1990). 근래에 들어 크리깅은 우수한 예측 성능이 확인되면서 공학분야에 적용되었으며, 국내외적으로 수문, 기상, 환경과학 등의 분야에서 크리깅을 이용한 다양한 연구가 수행되었다(Simpson et al., 2001; Webster and Oliver, 2007; Lim et al., 2007; Park and Jang, 2008; Shin et al., 2014). 특히, 수문/기상 분야 에서 크리깅은 강우의 공간분포를 파악하거나 면적우량 산정 에 이용되었으며, 다양한 원격탐사 자료를 통합하여 대상 인자의 공간분포를 예측하는데 사용되었다(Hevesi et al., 1992; Goovaerts, 2000; Yoo and Jung, 2001; Lee and Ryu, 2002; Yoon et al., 2004; Cho and Jeong, 2006; Jung et al., 2008; Heo and Park, 2009; Park et al., 2010; Kim et al., 2013).
크리깅에는 일반적으로 다음과 같은 두 가지 가정이 적용된다. 먼저, 크리깅을 적용할 대상 자료가 정규분포를 따라야 된다는 것이다. 대상 자료가 정규분포를 따르지 않을 경우 예측 변수와 종속변수가 선형이 되도록 변수 변환이 이루어진다. 이 때 크리깅으로 추정된 값은 쉽게 역변환 될 수 있지만 분산의 추정치는 그렇지 못하는 문제가 있다(Hengl et al., 2004). 다음으로 크리깅을 적용할 자료가 연속적이고 정상(stationarity)적 이어야 한다는 것이다. 대부분의 공간 자료는 특정 경향을 나타내거나 위치가 변함에 따라 평균이 바뀌는 문제가 있다. 경향성이 강하게 나타나는 자료에 크리깅을 적용할 경우 공간 적 의존성에 모형설정오류(mis-specification)가 발생하여 예측값이 편향될 수 있다(Karl, 2010). 따라서 자료의 경향성을 제거하여 크리깅을 적용해야 대상 자료의 공간적 특성을 반영한 예측값을 산정할 수 있다.
강우자료에 크리깅을 적용할 때 나타나는 가장 큰 문제는 강우자료가 크리깅의 이러한 가정을 만족시키지 못한다는 점이다. 강우 자료는 일반적으로 강한 양의 왜곡도를 나타내며, 간헐성도 강하게 나타난다. 경우에 따라 방향성도 크게 나타난다. 이로 인해 강우 자료를 이용하여 크리깅을 수행할 경우 예측값이 편향되어 나타나거나 왜곡될 가능성이 크다. 따라서 크리깅을 이용하여 정략적인 강우장을 추정하기 위해서는 정규분포가 아닌 왜곡된 분포를 따르는 강우 자료의 특성과 무 강우의 시공간적 분포 특성을 반영할 수 있는 기법의 개발이 필요하다.
본 연구에서는 강우 자료의 여러 특성 중 정규분포를 따르지 않는 특성에 집중하여 단순크리깅의 적용방법을 개선해 보고자 한다. 단순크리깅은 크리깅의 여러 방법 중 가장 단순한 경우이나, 설명이 쉽고, 아울러 적용사례를 비교하기 쉽다 는 장점이 있다. 또한 단순크리깅의 적용 기법을 개선할 경우 다른 복잡한 크리깅 기법에도 쉽게 적용이 가능하다. 본 연구에서는 모의자료와 레이더 강우에 단순크리깅을 수행하였고, 각 경우의 단순크리깅 결과를 비교하여 정규분포를 따르지 않는 자료가 강우 추정에 미치는 영향을 분석하였다.
2. 배경이론
2.1 단순크리깅(Simple Kriging)
크리깅은 이미 알고 있는 지점의 값을 선형조합하여 미지점의 값을 예측하는 지구통계적 기법이다(Cressie, 1990). Choi (2013)는 크리깅에 대하여 다음과 같이 정리하였다. 크리깅의 주요 목적은 미지점의 값을 예측하기 위해 적용할 가중치를 결정하는 것이다. 가중치 결정에는 일반적으로 예측값과 참값 사이의 오차가 최소가 되도록 하며, 추정값이 편향되지 않는다는 조건이 가정된다. 크리깅 추정식이 항상 편향되지 않기 위해서는 가중치의 합이 1이 되어야 한다. 가중치를 결정하는 방법에는 여러 가지가 있으며, 오차분산을 최소로 하여 가중치를 결정하는 경우를 단순크리깅(simple kriging)이라 한다. 이미 알려진 n개의 자료를 이용하여 단순크리깅으로 x0 지점 에서 미지값을 예측하는 방법은 Eq. (1)과 같고, 오차분산식은 Eq. (2)와 같다.
여기서, z0는 예측하고자 하는 참값,
Eq. (2)를 보면 오차분산은 참값과 예측값 차의 제곱에 대한 기대값으로 정의되며, 가중치의 함수이다. 이는 참값(z0)은 알려져 있지 않지만 상수이고 예측값
여기서, Cov(zi, zj)는 z(xi)와 z(xj) 사이의 분리거리에 따라 결정되는 공분산이다. Eq. (4)를 보면 오차분산은 가중치의 함수임을 알 수 있다. 오차분산을 각 가중치에 대하여 편미분하여 0이 되는 극값을 구하고, 두 번 편미분하여 그 값이 0보다 크면 오차분산을 최소로 하는 가중치를 구하게 된다. 이를 식으로 나타내면 Eq. (5)와 같고 편미분하여 정리하면 Eq. (6)과 같다.
Eq. (6)을 다시 λl에 대하여 편미분하면 2Cov(zl, zl)이 되고 이는 분산을 나타내므로 양의 값이 된다. 따라서 Eq. (6)을 만족하는 가중치들이 오차분산을 최소로 한다. Eq. (6)을 간단히 정리하면 Eq. (7)이 되며, 이를 크리깅방정식 또는 크리깅 연립방정식(system of n-equation)이라 한다.
Eq. (7)을 행렬방정식으로 구체적으로 나타내면 Eq. (8)과 같은 행렬식이 된다. 구체적으로 알려진 자료가 n개 있을 때 각 자료점 사이의 공분산과 예측지점 및 각 자료의 공분산으로 구성된 크리깅방정식을 풀어 가중치를 구한다. Eq. (8)에 주어진 행렬의 대각성분은 동일한 위치에 존재하는 자료의 공분산이므로 분산이 된다.
Eq. (8)에서 공분산은 베리오그램과 분리거리를 이용하여 산정하므로 크리깅 기법을 사용하기 위해서는 반드시 베리오그램 모델링이 선행되어야 한다. 일반적으로 경험적 베리오그램을 먼저 산정하고 이에 적합한 이론적 베리오그램을 결정 한다. 경험적 베리오그램은 Eq. (9)로 계산한다.
위 식에서 γ(h)는 베리오그램 값을 나타내고, n은 관측 지점의 수, R(xi)는 관측 지점의 값을 나타낸다. Eq. (9)를 보면 베리오그램은 자료간 차의 제곱합을 이용한 값으로 자료간 분산과 유사한 값임을 알 수 있다.
경험적 베리오그램이 계산되면 이를 관측소 간 거리에 따라 그래프로 나타낸 후 상관거리(correlation length), 문턱값(sill height), 너깃(nugget) 성분을 결정한다. 상관거리는 베리오그램에서 자료들이 상관관계를 보이는 최대 분리거리이고, 문턱 값은 상관거리에서 베리오그램이 가지는 일정한 값으로 자료의 분산을 나타내기도 한다. 너깃은 관측소간 거리가 0일 때 베리오그램이 0이 되지 않는 경우로 이미 알고 있는 지점들 사이의 가장 짧은 거리보다 작은 거리에서 급경한 값의 변화가 일어날 때 나타난다. 경험적 베리오그램이 결정되면 이에 적합한 이론적 베리오그램을 결정해야 한다. 이론적 베리오그 램에는 Eqs. (10)~(12)와 같은 구형모형, 지수모형, 가우스모 형 등이 있다.
여기서, C0는 문턱값, a는 상관거리, h는 자료간 거리를 나타낸다. 지수모형과 가우스모형은 상관거리 a에서 정확한 문턱 값을 갖지 않아 문턱값의 95%에 해당하는 값을 주는 분리거리를 실제적인 상관거리(actual range)로 가정한다. 상기와 같은 베리오그램 중 경험적 베리오그램과 가장 유사한 형태의 모형을 최종적인 베리오그램으로 결정한다. 일반적으로 가우스모형은 작은 분리거리에서 자료들이 강한 상관성을 나타내 거나 연속성이 강한 자료를 분석하는데 이용되므로 정규분포를 따르는 자료에 적합한 특성이 있다. 자료에 적합한 이론적 베리오그램이 결정되면 크리깅 행렬방정식의 성분인 공분산은 다음 식을 이용하여 산정할 수 있다.
위 식에서 Cov(h)는 자료의 공분산, h는 관측소간 거리, σ2 는 자료의 분산, γ(h)는 앞에서 산정한 베리오그램을 나타낸다. 위와 같은 방법으로 크리깅 행렬방정식의 공분산을 결정 할 수 있고, 크리깅 행렬방정식이 구성되면 이 행렬방정식을 풀어 크리깅의 가중치를 결정할 수 있다. 가중치가 결정되면 각 관측소의 자료와 함께 크리깅 예측식에 적용하여 미지점에서의 값을 산정할 수 있다.
2.2 자료특성에 따른 상관계수의 변화
크리깅 과정 중 크리깅 행렬방정식을 구성하기 위해서는 행렬 성분의 근간이 되는 관측소 사이의 공분산이 필요하다는 것을 앞에서 확인하였다. 일반적으로 확률변수 X의 증감에 따른 확률변수 Y의 증감의 방향과 정도를 정규화하지 않고 나타낸 것이 공분산이고, 이를 정규화한 것이 상관계수(correlation coefficient)이다. 따라서 공분산은 상관계수와 Eq. (14)와 같은 관계를 갖는다.
여기서 Cov(X, Y)는 X, Y 자료에 대한 공분산, ρ는 두 자료의 상관계수 σX, σY는 각 자료의 표준편차를 나타낸다. 위 식을 통해 공분산은 자료간 상관계수에 직접적으로 영향을 받음을 알 수 있다. 상관계수는 자료가 어떤 분포를 따르는가에 따라 다르게 나타난다. 예를 들어 자료가 정규분포를 따르는 경우와 대수정규분포를 따르는 경우에 대해 상관계수는 다르게 결정된다. 이를 Ang and Tang(2007)에 나타난 대수정규분포 에 관한 이론을 바탕으로 살펴보면 다음과 같다.
먼저, 대수정규분포를 따르는 변량 X의 평균과 분산은 다음 과 같이 나타난다.
여기서 λ와 ζ는 대수정규분포의 모수로 lnX의 평균과 표준편차를 나타낸다. 평균과 분산에 대한 위와 같은 관계를 이용하면 Eq. (14)와 같은 공분산은 기대값 정리에 의해 결정할 수 있다. 공분산에 대한 기대값 정리는 Eq. (17)과 같고, 이를 평균과 분산에 대한 Eqs. (15)와 (16)으로 나타내면 Eq. (18)과 같다.
위와 같은 관계식을 Eq. (14)에 적용하면 대수정규분포를 따르는 자료의 상관계수를 결정할 수 있다. 먼저, 두 변량 Z1, Z2가 대수정규분포를 따른다고 하고 여기에 대수를 취한 변량 X1, X2가 정규분포를 따른다고 하자. 또한 X1과 X2의 평균과 분산을 각각 μ1, μ2 및 σ12, σ22라 하고 둘 사이의 상관계수를 ρ라고 하면, Z1과 Z2 사이의 상관계수는 다음과 같이 유도된다.
Eq. (19)에서 좌측의 식은 Eq. (14)를 상관계수에 관해 정리 한 것과 같은 식으로 일반적으로 정규분포를 따르는 자료의 상관계수를 나타낸다. 그러나 자료가 대수정규분포를 따르게 되면 Eq. (19)의 우측의 식과 같이 상관계수가 정규분포를 따르는 자료의 경우와 다르게 나타난다. 따라서 자료가 대수정 규분포를 따르는 경우와 정규분포를 따르는 경우에 상관계수의 형태가 다르게 나타난다는 것을 알 수 있다. 이는 결과적으로 베리오그램의 형태를 결정하게 되고 공분산 계산에 영 향을 주어, 크리깅 가중치에 영향을 미치게 된다. 즉, 자료특성에 따라 크리깅 예측값이 다르게 생성될 수 있음을 나타낸다.
3. 적용사례
3.1 모의자료를 이용한 단순크리깅 결과 분석
3.1.1 모의자료
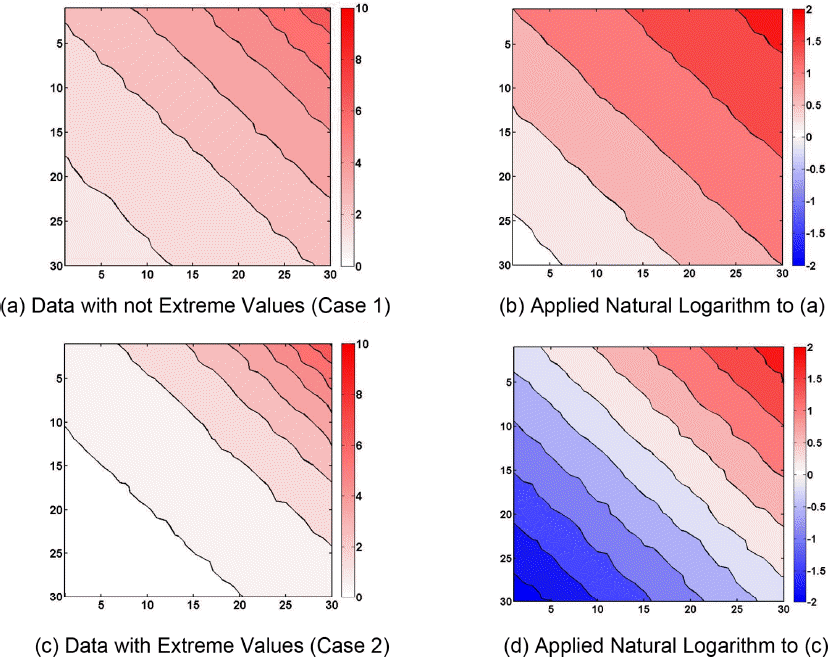
본 연구에서는 자료의 비정규적 특성이 단순크리깅에 미치는 영향을 분석하기 위해 먼저 모의자료를 이용한 분석을 수행하였다. 자료는 30 km×30 km의 영역에 1 km×1 km마다 한 값을 갖도록 하여 총 900개의 값으로 구성되도록 하였다. 자료는 0보다 크고 10이하의 값을 갖도록 하였으며, 대각선 방향으로 유사한 값이 분포하도록 생성하였다. 본 연구에서는 두 가지 Case의 원자료를 생성하였다. 생성한 두 자료는 모두 정규분포를 따르지 않도록 하였으며, 한 자료는 다른 자료와 달리 극단적인 값을 갖도록 하였다. 이는 대수정규분포가 오른쪽으로 왜곡되어 있는 특성을 이용하여 한 자료가 다른 자료에 비해 비정규적 특성이 강하게 나타나도록 하기 위함이다. 자료의 비정규성이 단순크리깅에 미치는 영향을 평가하기 위해 본 연구에서는 이와 같이 생성된 원자료와 여기에 자연 로그를 적용한 자료를 이용하였다. 각 Case 별로 생성된 원자료와 자연로그를 적용하여 나타낸 자료는 Fig. 1과 같다.
Generated Data Field for Simple Kriging
Fig. 1에서 (a)는 극단적인 값이 포함되지 않은 자료로 Case 1의 경우를 나타내고, (c)는 극단적인 값이 포함된 Case 2의 경우를 나타낸다. 두 자료는 모두 10 이하의 값이 분포되어 있다. 극단적인 값은 자료의 평균에 비해 매우 큰 값을 나타내는 것으로 그림에서 Case 2는 Case 1보다 자료의 중앙과 우측 상단의 값의 차가 크게 나타난 것을 알 수 있다. Fig. 1 의 (b), (d)는 각 Case 별로 생성한 원자료에 자연로그를 적용한 자료를 나타낸다. 각 그림에서 좌측 하단부는 작은 값이 분포되어 있고, 우측 상단으로 갈수록 큰 값이 분포되어 있다. 그림에서 확인할 수 있듯이 극단적인 값이 포함되지 않은 Fig. 1(a)의 경우 자료간 증가 폭이 균등하여 등고선 간격이 전체적으로 넓고 균등하게 나타났다. 반면, 극단적인 값이 포함된 Fig. 1(c)는 자료의 증가 폭이 일정하지 않아 우측 상단으로 갈수록 등고선 간격이 조밀하게 나타났다. 이는 비정규성이 약하게 나타난 Case 1의 원자료는 비교적 정규분포에 근사함을 나타내고, 극단적인 값이 포함된 Case 2의 원자료는 비정규분포의 특성이 크게 나타남을 의미한다. 자연로그를 적용한 자료는 두 경우 모두 비교적 등고선 간격이 동일하게 나타났고, 원자료에 극단적인 값이 포함되지 않았던 Fig. 1의 (b)가 (d)보다 등고선 간격이 더 넓게 나타났다. 또한, Case 2 의 경우 자연로그를 적용하였을 때 원자료에서 매우 작은 값 이 분포한 좌측 하단에서 일부 구역에 음의 값이 나타나기도 하였다. Fig. 1과 같이 생성된 각 자료의 평균과 분산을 정리하면 Table 1과 같다.
Mean and Variance of Generated Data
Table 1에서 알 수 있듯이, 원자료에서 비정규성이 강하게 나타난 Case 2가 Case 1보다 평균은 작고 분산은 크게 나타났다. 자연로그를 적용한 자료의 경우 Case 2에서는 음의 값이 생성되면서 평균이 0에 근사하게 나타났고, 분산은 Case 1 보다 크게 나타났다. 본 연구에서는 위와 같이 생성된 자료를 이용하여 자료의 비정규적 특성이 단순크리깅 예측에 미치는 영향을 평가하였다. 이를 위해 각 자료에 대해 정규성을 가정한 경우와 비정규성을 가정한 경우에 단순크리깅을 수행하고, 이를 원자료의 분포와 비교하였다.
3.1.2 모의자료를 이용한 베리오그램 모델링
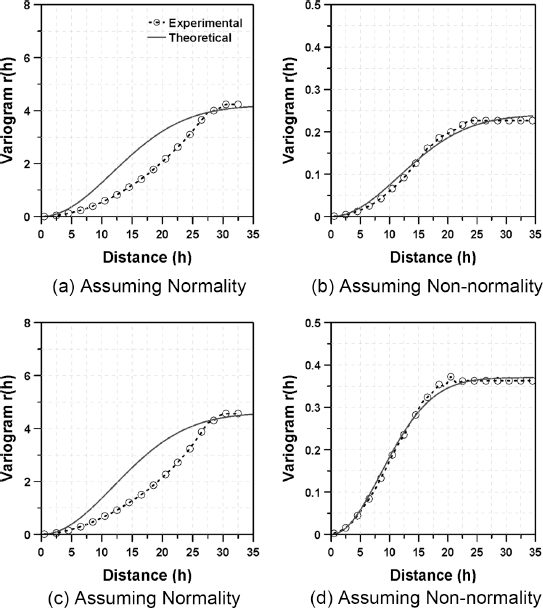
본 연구에서는 Fig. 1의 자료를 이용하여 단순크리깅을 수행하기 위해 먼저 자료에 적합한 형태의 베리오그램을 유도 하였다. 이를 위해 자료의 경험적 베리오그램을 나타내고, 이에 적합한 형태의 이론적 베리오그램을 유도하였다. 먼저, 원자료인 Fig. 1(a), (c)의 자료가 정규분포를 따른다고 가정하여 베리오그램을 유도하였다. 다음으로 원자료의 비정규성을 가정하고 자연로그를 적용한 Fig. 1(b), (d)의 자료를 이용하여 베리오그램을 유도하였다. 본 연구에서는 정규분포를 따르는 자료에 적합한 식 (12)의 가우스모형을 이용하여 베리오그램을 유도하였다. 베리오그램의 유도에는 경험적 베리오그램과의 차의 제곱이 최소가 되도록 하는 최소자승법을 이용하였다. 유도된 베리오그램을 그림으로 나타내면 Fig. 2와 같고, 문턱값과 실제적인 상관거리를 정리하여 나타내면 Table 2와 같다.
Experimental Variogram and Theoretical Variogram of Generated Data (Top: Case 1, Bottom: Case 2)
Sill Heights and Actual Ranges of Variogram in the Case of Using Generated Data
Fig. 2에서 점선은 경험적 베리오그램, 실선은 가우스모형을 이용하여 유도한 이론적 베리오그램을 나타낸다. 그림에서 알 수 있듯이 정규분포를 따르지 않는 원자료에 정규성을 가정한 경우 가우스모형으로 적합한 베리오그램을 유도하기 어려운 것으로 나타났다. 반면, 원자료의 비정규성을 가정하여 자연로그를 적용한 자료를 이용한 경우 가우스모형으로 적합한 베리오그램이 결정된 것으로 나타났다. 이는 자연로그를 적용한 자료의 베리오그램의 형태가 S 곡선 형상의 가우스모 형과 유사하게 나타났기 때문이다. 또한 정규분포를 따르지 않는 원자료의 경우 베리오그램이 지수곡선의 형태로 나타나 가우스모형과 다르게 나타났기 때문이다.
Table 2에서 자료의 정규성을 가정한 경우 문턱값은 Case 1 에서는 4.2, Case 2에서는 4.6으로 경험적 베리오그램의 끝 값이 결정된 것을 알 수 있다. 이는 베리오그램에 자료의 특성이 제대로 반영되지 않아 부적합하게 결정된 값이다. 반면, 자료의 비정규성을 가정한 경우 문턱값은 Case 1에서는 0.24, Case 2에서는 0.37로 경험적 베리오그램의 수렴부와 유사한 값으로 결정되었다. 상관거리는 자료의 비정규성을 가정한 경우 Case 1에서는 28 km, Case 2에서는 21 km로 비교적 크게 나타났지만, 경험적 베리오그램과 유사한 값이 결정되었다. 이는 본 연구에서 생성한 자료의 상관정도가 비교적 크다는 것을 나타낸다. 반면, 자료의 정규성을 가정한 경우에는 문턱 값이 적절히 결정되지 않아 원점에서 경험적 베리오그램의 끝 부분까지의 거리가 상관거리로 결정되었다.
이러한 결과를 통해 정규분포를 따르지 않는 자료에 정규성을 가정하여 베리오그램을 유도하면 적합한 문턱값과 상관거리를 갖는 베리오그램을 결정하기 어려움을 알 수 있다. 이는 단순크리깅을 수행할 때 부적합한 예측 결과를 생성하는 문제를 야기할 수 있다.
3.1.3 모의자료를 이용한 단순크리깅 예측
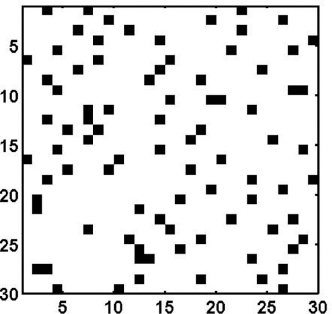
본 연구에서는 Fig. 1의 자료에서 임의 지점의 값을 무작위로 선정하여 남긴 후, Fig. 2에서 유도한 베리오그램을 적용하여 단순크리깅을 수행하였다. 임의로 선정한 자료는 전체의 10%에 해당하는 90개로 그 위치를 그림으로 나타내면 Fig. 3 과 같다.
Randomly Selected Location from Generated Data
본 연구에서는 자료의 비정규적 특성이 단순크리깅에 미치는 영향을 평가하기 위해 다음과 같은 방법으로 단순크리깅을 수행하였다. 먼저, 자료의 정규성을 가정하고 유도한 베리오그램을 Fig. 1의 (a), (c)에서 임의로 선정한 지점 자료에 적용하여 단순크리깅을 수행하였다. 다음으로 자료의 비정규성을 가정하고 유도한 베리오그램을 Fig. 1의 (b), (d)에서 임의로 선정한 지점 자료에 적용하여 단순크리깅을 수행한 후, 결과에 지수를 적용하여 나타내었다. 본 연구에서는 이와 같이 생성된 두 결과를 원자료의 분포와 비교하였다. 이를 그림으로 나타내면 Fig. 4와 같다.
Simple Kriging Results for Generated Data (Top: Case 1, Bottom: Case 2)
Fig. 4는 각 Case 별로 왼쪽부터 임의 지점의 자료, 자료의 정규성을 가정한 경우의 단순크리깅 결과, 자료의 비정규성을 가정하여 단순크리깅을 수행한 후 지수를 적용하여 나타낸 결과 그리고 원자료를 나타낸다. 그림에서 확인할 수 있듯이, 자료의 정규성을 가정하여 단순크리깅을 수행하였을 때는 Case 1의 경우 예측값이 작게 나타난 부분도 있지만, 비교적 원자료와 가장 유사하게 나타났다. 이는 Case 1의 경우 원자료에 극단적인 값이 없어 비정규성이 약하고 정규분포의 특 성에 근사하게 나타나 정규성을 가정한 단순크리깅 결과가 더 양호하게 나타난 것이다. 이 경우 Fig. 2와 같이 베리오그램이 적절하게 나타나지 않아도 비정규성이 약하게 나타난 자료에 대해서는 정규성을 가정한 결과가 더 우수할 수 있음을 나타낸다. 그러나 원자료에 극단적인 값이 포함되어 비정규성이 강하게 나타난 Case 2는 정규성을 가정한 경우 전체적으로 등고선이 흐트러지고 예측값도 작게 나타났다. 특히, Case 2에서는 일부 지점에서 단순크리깅 예측값이 음의 값으로 생성되면서 원자료의 분포와 다른 결과가 나타났다. 이는 유도한 가우스모형이 원자료 특성을 적절하게 반영하고 있지 않아 단순크리깅 결과가 부적절하게 나타난 것으로 볼 수 있다.
자료의 비정규성을 가정하여 단순크리깅을 수행하였을 때는 Case 1의 경우 정규성을 가정한 결과보다 양호하게 나타나지는 않았다. 반면, 원자료에 극단적인 값이 포함되어 비정규성이 강하게 나타났던 Case 2의 경우 등고선 형태가 흐트러졌지만 비교적 원자료의 분포와 유사한 결과가 나타났다. 그러나 이 경우에는 원자료에서 극단적인 값이 분포한 우측 상단 부분에서 단순크리깅 결과가 원자료보다 크게 나타나는 문제가 발생하였다. 이는 자료간 상관정도가 크다면 원자료에서 큰 값이 분포한 구역에서는 단순크리깅으로 예측된 값이 크게 왜곡되어 나타날 수 있기 때문이다. Fig. 2의 베리오그램에서 알 수 있듯이 본 연구에 적용한 자료의 상관정도는 비교적 크게 나타난 것을 알 수 있다. 상기와 같이 나타난 단순크리깅 결과와 원자료 사이의 검정통계량을 비교한 결과는 Table 3과 같다.
Test Statistics of Simple Kriging Results Using Generated Data
Table 3에서 RMSE는 자료의 정규성을 가정하여 단순크리깅을 수행한 경우가 자료의 비정규성을 가정한 경우보다 작 은 값으로 나타났다. 특히 Case 1에서는 자료의 정규성을 가정한 경우 RMSE가 0.22로 원자료와 거의 동일하게 나타난 것을 알 수 있다. 이는 극단적인 값이 없어 비정규성이 약하게 나타난 자료의 경우 정규성을 가정한 단순크리깅 결과가 비정규성을 가정한 결과보다 양호할 수 있음을 나타낸다. 이는 Fig. 4의 결과를 통해서도 확인할 수 있다. Case 2에서는 자료의 정규성을 가정한 경우에 RMSE가 더 작게 나타났지만 비정규성을 가정한 경우와 비교하여 크게 차이가 나타나 지 않았다. 이는 Fig. 4에서 확인할 수 있듯이 정규성을 가정한 경우 단순크리깅 예측 결과가 원자료와 비교하여 부적절하게 나타났기 때문이다.
BS는 모든 경우에 대해 1과 근사한 값으로 나타났다. 자료 의 정규성을 가정한 경우에는 BS가 1보다 조금 작은 값으로 단순크리깅 예측값의 합이 원자료의 합보다 작게 나타난 것을 알 수 있다. 반면, 자료의 비정규성을 가정한 경우 BS가 1 보다 조금 큰 값으로 예측값의 합이 원자료의 합보다 크게 나타난 것을 알 수 있다.
평균은 Case 1과 Case 2 모두 자료의 정규성을 가정한 경 우와 비정규성을 가정한 경우의 단순크리깅 결과가 원자료와 유사하게 나타났다. 그러나 최대값은 자료의 정규성을 가정한 경우에서는 원자료보다 작은 값이, 자료의 비정규성을 가정한 경우에서는 원자료보다 큰 값이 나타났다. 특히, Case 2의 경 우 원자료의 최대값은 8이었지만, 단순크리깅 결과 최대값은 14로 매우 크게 나타났다. 이는 자료간 상관정도가 크면, 단순 크리깅으로 원자료보다 크게 왜곡된 값이 생성될 수 있음을 나타낸다.
본 연구에서는 이러한 결과를 통해 비정규성이 약한 자료의 경우 정규성을 가정한 단순크리깅 결과가 비정규성을 가정한 결과보다 양호할 수 있음을 확인하였다. 그러나 극단적인 값 이 포함되어 비정규성이 강한 자료의 경우 비정규성을 가정 하여 단순크리깅을 수행한 결과가 정규성을 가정한 결과보다 우수하다는 것을 알 수 있었다. 아울러 자료간 상관정도가 크다면 자료의 비정규성을 가정하여 단순크리깅을 수행한 경우 예측 결과가 원자료보다 크게 나타날 수 있음을 확인하였다.
3.2 레이더 강우를 이용한 단순크리깅 결과 분석
3.2.1 대상자료
본 연구에서는 강우 자료의 비정규성이 단순크리깅에 미치는 영향을 분석하기 위해 관악산 레이더 강우 자료를 이용하 였다. 관악산 기상 레이더는 경기도 과천시 중앙동에 위치하고 있고, 위도 37°26′28″, 경도 126°57′58″, 고도 637 m인 지점에 설치되어 있다. 관악산 레이더는 우리나라 최초의 기상 레이더로 S-밴드를 사용하고 있으며, 약 100 km 정도의 유효 관측반경을 갖고 있다. 관악산 레이더 유효관측반경 내에는 약 111개의 기상청과 국토교통부 산하의 강우관측소가 설치 되어 있다. 본 연구에서는 강우관측소가 공간적으로 비교적 균등하게 분포한 영역에 단순크리깅을 적용하기 위해 레이더 관측반경 50 km 정도에 분포하고 있는 지상관측소의 자료를 이용하였다. 해당영역에는 90개의 기상청과 국토교통부 산하의 강우관측소가 있으며, 본 연구에서는 관측소 위치의 레이더 강우 자료를 이용하였다. 관악산 레이더 자료는 500 m× 500 m의 해상도를 갖고 있으며, 본 연구에서는 1 km×1 km 해상도의 레이더 강우 자료를 적용하였다. 관악산 레이더 관측범위 내 지상 강우관측소의 위치 및 단순크리깅을 적용할 영역을 나타내면 Fig. 5와 같다.
Location of Gwanaksan Radar (KWK) Site and Rain Gauges
Fig. 5에서 알 수 있듯이 관악산 레이더 관측반경 내 위치한 지상관측소는 서쪽의 해안지역보다 동쪽의 내륙지역에 집중 되어 있다. 레이더 관측반경 50 km 정도의 영역은 서울시와 경기도를 포함하고 있다. 해당영역 내 강우관측소는 서울시를 제외하고 다른 지역에 비해 균등하게 분포하고 있으며, 서울시는 다른 지역에 비해 관측소가 밀집되어 있다. Fig. 5에서 확대하여 나타낸 단순크리깅을 적용할 범위는 100 km×100 km 를 나타낸다.
본 연구에서는 2014년 5월 25일과 6월 3일에 발생한 두 호우사상을 적용하였다. 서울 지점의 경우 5월 25일에는 일강우량이 21 mm, 6월 3일에는 일강우량이 33 mm로 나타났다. 2014년 기상월보에는 2014년 5월 하순 경 우리나라 남쪽으로 이동성 고기압이 통과하면서 평균강수량이 11.3 mm로 평년 대비 37%인 것으로 나타나 있다. 또한, 2014년 6월에 우리나 라는 이동성 고기압의 영향을 주로 받았으며, 2~4일에는 서쪽에서 다가온 저기압의 영향으로 전국 대부분 지방에 비가 내린 것으로 나타나 있다. 특히, 6월 상순에는 평균강수량이 35.8 mm로 평년대비 102% 수준으로 기록되어 있다(KMA, 2014). 본 연구에서는 두 호우사상 중 강우가 가장 많이 나타난 5월 25일 23시와 6월 3일 6시 20분 2개 시점의 자료를 이용하여 단순크리깅을 수행하였다. 두 시점 자료에 대한 레이더 강우 영상을 나타내면 Fig. 6과 같다. 여기서 레이더 강우는 관악산 레이더 반사도 자료에 Marshall-Palmer 관계식을 이용하여 산정된 값이다.
Weather Radar Image of the Rainfall Event
Fig. 6에서 알 수 있듯이 5월 25일 사상의 경우 북동쪽으로 호우의 방향성이 나타남을 알 수 있고, 6월 3일 사상은 상대적으로 방향성이 작게 나타난 것을 알 수 있다. 강우 면적은 5월 25일보다 6월 3일의 경우가 더 크게 나타났다. 또한, 6월 3일 자료에서 확인할 수 있듯이 관악산 레이더가 위치한 중심 부근에서 남쪽으로 레이더 강우가 차폐되는 지역이 있음을 알 수 있다. 강우강도는 두 경우에서 10 mm/hr 이하로 해당 시점에 대해 크지 않게 나타났다. 본 연구에서는 위와 같이 나타난 자료에서 지상관측소가 최소로 관측할 수 있는 값인 0.5 mm/hr보다 작은 크기로 나타난 지역은 무강우로 판단하였다.
본 연구에서는 강우 자료의 비정규성만이 단순크리깅에 미치는 영향을 분석하기 위해 베리오그램의 유도에는 무강우 구역을 우량계 최소 관측값인 0.5 mm/hr로 채운 자료를 적용 하였다. 본 연구에서는 레이더 강우가 정규분포를 따른다고 가정했을 경우와 그렇지 않다고 가정했을 경우에 단순크리깅을 수행하고, 이를 원자료와 비교하였다. 자료의 정규성을 가정한 경우에는 레이더 강우 자료를 그대로 이용하였다. 자료의 비정규성을 가정한 경우에는 자연로그를 적용한 레이더 강우를 이용하여 단순크리깅을 수행하였고, 예측 결과에 지수를 적용하여 나타내었다. 본 연구에 사용한 레이더 강우 자료, 무강우 부분을 0.5 mm/hr를 채워 넣은 자료, 여기에 자연로그를 적용한 자료의 평균과 분산을 정리하여 나타내면 Table 4 와 같다.
Mean and Variance of Radar Rainfall Data
Table 4에서 알 수 있듯이 레이더 강우의 평균은 0.45, 1.11 mm/hr로 크지 않지만, 분산이 평균에 비해 크게 나타난 자료임을 알 수 있다. 무강우를 0.5 mm/hr로 채워 넣은 자료는 레이더 강우보다 평균은 크고 분산은 작게 나타났다. 자연로그를 적용한 자료는 평균이 음의 값으로 나타났고, 분산도 다른 경우에 비해 가장 작게 나타났다. 이는 적용한 자료의 강우강도가 크지 않다는 것을 나타낸다. 위와 같은 자료를 이용하여 본 연구에서는 레이더 강우의 비정규적 특성이 단순 크리깅에 미치는 영향을 평가하였다.
3.2.2 레이더 강우 자료를 이용한 베리오그램 모델링
본 연구에서는 Fig. 6의 자료를 이용하여 단순크리깅을 수행하기 위해 먼저 자료에 적합한 베리오그램을 유도하였다. 베리오그램은 레이더 강우 자료의 정규성을 가정한 경우와 비정규성을 가정한 경우에 대해 2가지로 유도하였다. 자료의 정규성을 가정한 경우 무강우를 0.5 mm/hr로 채워 넣은 자료를 이용하였다. 자료의 비정규성을 가정한 경우에는 자연로그를 적용한 자료를 이용하여 베리오그램을 유도하였다. 이론적 베리오그램은 모의자료의 분석과 동일한 방법으로 가우스모 형을 이용하여 유도하였고, 최소자승법을 이용하여 최적의 베리오그램을 결정하였다. 각 경우에 대한 베리오그램을 그림으로 나타내면 Fig. 7과 같고, 문턱값과 실제적인 상관거리를 정리하여 나타내면 Table 5와 같다.
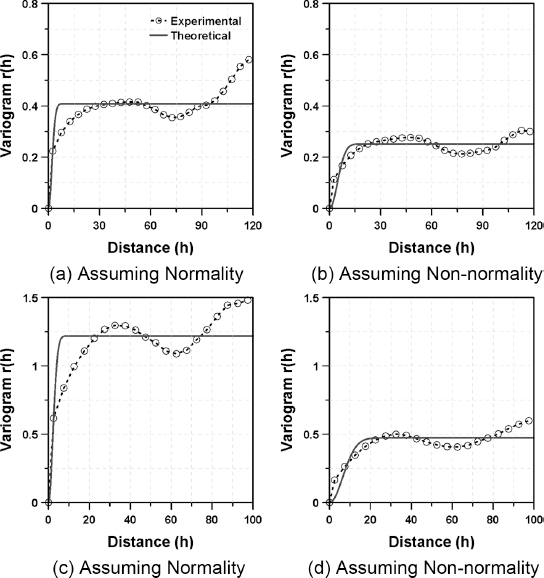
Experimental Variogram and Theoretical Variogram of Radar Rainfall Data (Top: 2014. 05. 25. 23:00, Bottom: 2014. 06. 03. 06:20)
Sill Heights and Actual Ranges of Variogram in the Case of Using Radar Rainfall Data
Fig. 7에서 점선은 경험적 베리오그램, 실선은 가우스모형을 이용하여 유도한 이론적 베리오그램을 나타낸다. 그림에서 알 수 있듯이 레이더 강우 자료는 정규분포를 따르지 않기 때문에 가우스모형으로 적합한 베리오그램을 유도하기 어려운 것을 알 수 있다. 이는 레이더 강우 자료의 경험적 베리오그 램이 지수곡선의 형태로 나타나 가우스모형으로 적절한 수렴 구간을 찾기 어렵기 때문이다. 반면, 레이더 강우 자료의 비정 규성을 가정한 경우에는 가우스모형으로 적합한 베리오그램이 결정된 것을 알 수 있다. 이 경우 가우스모형이 경험적 베리오그램의 수렴구간을 적절하게 모의하는 것으로 나타났다.
Table 5에서 두 사상에 대해 레이더 강우의 정규성을 가정한 경우에는 문턱값이 0.41, 1.22로 경험적 베리오그램과 다르게 나타난 것을 알 수 있다. 반면, 레이더 강우의 비정규성을 가정한 경우에는 두 사상에 대해 문턱값이 0.25, 0.47로 경험적 베리오그램에 적합한 값으로 결정되었다. 상관거리는 레이더 강우의 정규성을 가정한 경우에는 5 km로 경험적 베리오그램보다 작게 나타났지만, 비정규성을 가정한 경우에는 10 km 이상으로 적절한 값이 결정되었다.
이러한 결과를 통해 레이더 강우가 정규분포를 따르지 않으므로 자료의 정규성을 가정하여 접근하면 적합한 베리오그램을 결정하기 어려움을 알 수 있다. 따라서 레이더 강우 자료에 단순크리깅을 적용할 때는 자료의 비정규성을 가정하여 자연로그를 적용한 자료를 이용해야 주어진 자료에 적합한 베리오그램을 유도할 수 있다.
3.2.3 레이더 강우 자료를 이용한 단순크리깅 예측
본 연구에서는 관악산 레이더 관측반경 50 km 내에 위치한 90개 지상관측소의 레이더 강우에 Fig. 7의 베리오그램을 적용하여 단순크리깅을 수행하였다. 자료의 비정규성이 단순크 깅에 미치는 영향을 평가하기 위해 본 연구에서는 모의자료의 분석과 동일한 방법을 적용하였다. 먼저, 레이더 강우의 정규성을 가정하고 유도한 베리오그램을 이용하여 단순크리깅을 수행하였다. 다음으로 레이더 강우의 비정규성을 가정하고 자연로그를 적용한 자료로 유도한 베리오그램으로 단순크 리깅을 수행한 후, 결과에 지수를 적용하여 나타냈다. 본 연구에서는 이와 같이 생성된 두 개의 예측 결과를 원자료의 분포와 비교하였다. 이를 정리하여 나타내면 Fig. 8과 같다. 참고로 아래 결과는 레이더 자료가 갖고 있는 비등방성의 문제를 고려하지 않은 결과이다.
Simple Kriging Results for Radar Rainfall Data(Top: 2014. 05. 25. 23:00, Bottom: 2014. 06. 03. 06:20)
Fig. 8(a), (e)에서 작은 사각형은 레이더 강우가 무강우로 판단된 것을 나타낸다. 위 그림에서 알 수 있듯이 자료의 비등방성 문제를 고려하지 않고 단순크리깅을 적용했기 때문에 예측 강우는 원자료에서 강우가 강하게 나타난 부분을 중심으로 원형의 형태로 나타났다. 자료의 정규성을 가정하여 단순크리깅을 수행한 경우 레이더 강우 자료에서 강도가 작게 나타났던 부분은 무강우로 판단되어 전체 강우면적이 작게 나타나는 문제가 발생하였다. 반면, 자료의 비정규성을 가정하여 단순크리깅을 수행한 경우에는 레이더 강우 자료에서 강도가 작게 나타났던 부분이 0.5~1 mm/hr이하의 작은 값으로 생성되었다. 두 결과를 레이더 강우 자료와 비교하면 전체 강우 면적은 감소한 것으로 나타났지만, 자료의 비정규성을 가정한 경우가 대체로 원자료와 근사하게 나타난 것을 알 수 있다.
그러나 자료의 비정규성을 가정하여 단순크리깅을 수행한 경우 레이더 강우 자료의 최대값보다 큰 왜곡된 값이 나타나는 문제가 발생하였다. 이는 모의자료를 이용한 분석에서도 나타난 문제로 Fig. 8의 단순크리깅 결과에서 일부 구역에 진한 색으로 나타난 부분이다. 이 부분 주변에 분포한 관측소의 자료를 보면, 대체로 레이더 강우가 크게 나타났던 주변 부분에 대해 크리깅 예측값이 크게 나타난 것을 알 수 있다. 특히 본 연구에서는 상관거리가 11, 15 km로 나타났는데, 강우가 크게 나타난 부근의 관측소 주변에는 해당 상관거리 내 많은 수의 관측소가 분포하고 있음을 알 수 있다. 대체로 이러한 구역은 서울시를 나타내고 있는데, 서울시에는 Fig. 5처럼 인접한 관측소 사이의 거리가 본 연구에서 결정된 상관거리보다 작은 곳이 많이 분포되어 있다. 이러한 구역에서는 인접한 관측소 간 상관정도가 크게 나타나 크리깅으로 큰 강우가 생성될 수 있는 문제점이 있다. 위와 같이 나타난 단순크리깅 결과와 레이더 강우 자료 사이의 검정통계량을 비교하면 표 6 과 같다.
Table 6에서 확인할 수 있듯이, 레이더 강우의 정규성을 가정하여 단순크리깅을 수행한 경우는 강우가 작게 생성되었고, 비정규성을 가정한 경우에는 큰 강우가 생성되었다. RMSE는 5월 25일 사상에서는 레이더 강우의 비정규성을 가정한 경우가 정규성을 가정한 경우보다 1.2% 정도 작게 나타났지만, 6월 3일 사상에서는 80.7% 정도 크게 나타났다. 이는 5월 25일 사상의 경우 Fig. 8에서 알 수 있듯이 자료의 정규성을 가정한 결과와 비정규성을 가정한 결과가 크게 차이가 나지 않 아 RMSE가 크게 개선되지 않은 것이다. 반면, 6월 3일 사상에서는 자료의 비정규성을 가정하였을 때 일부 지역의 예측 강우가 레이더 강우보다 크게 나타나 RMSE가 정규성을 가정한 경우보다 크게 나타난 것이다.
Test Statistics of Simple Kriging Results Using Radar Rainfall Data
BS는 레이더 강우의 정규성을 가정하여 단순크리깅을 수행한 경우 두 호우사상에 대해 0.16, 0.18로 작게 나타났다. 그러나 비정규성을 가정하여 단순크리깅을 수행한 경우 5월 25일 자료는 0.53, 6월 3일 자료는 1.14로 정규성을 가정한 경우 보다는 상대적으로 1에 가깝게 나타났다. 이는 단순크리깅으로 일부 지역에 큰 값이 형성되기도 했지만 전체 영역에 대한 예측 강우의 합이 레이더 강우의 합과 비교적 유사하게 나타난 것을 나타낸다.
평균은 자료의 정규성을 가정한 경우에는 강우가 작게 예측 되어 레이더 강우와 상이하게 나타났지만, 비정규성을 가정한 경우에는 비교적 레이더 강우와 유사하게 나타났다. 최대값은 자료의 정규성을 가정한 경우 원자료보다 작게 나타났지만, 비정규성을 가정한 경우 6월 3일 사상에서는 레이더 강우의 2배 이상 되는 값이 나타났다. 레이더 강우와 비교한 이와 같은 단순크리깅 결과를 보다 쉽게 나타내기 위해 추가로 1:1 플롯을 작성하여 나타내면 Fig. 9와 같다.
Comparison of Radar Rain Rate and Simple Kriging Results(Top: 2014. 05. 25. 23:00, Bottom: 2014. 06. 03. 06:20)
Fig. 9에서 확인할 수 있듯이 두 호우사상 자료에 대한 단순 크리깅 결과는 정규성을 가정하였을 때는 레이더 강우보다는 과소 추정 되는 경향이 나타났다. 반면 자료의 비정규성을 가정하여 생성한 단순크리깅 결과는 레이더 강우와 유사한 크기의 값이 생성되는 경우도 많았지만 보다 과대 추정된 것으로 나타났다. 이는 Table 6에서 비교한 통계량이 정규성을 가정한 경우에 작게 나타났고, 비정규성을 가정하였을 때 크게 나타난 결과와 동일하다.
본 연구에서는 이러한 결과를 통해 레이더 강우의 정규성보다 비정규성을 가정하여 단순크리깅을 수행할 때 비교적 원자료에 적합한 예측 결과를 생성할 수 있음을 확인하였다. 그러나 모의자료의 경우처럼 자료의 비정규성을 가정하여 단순 크리깅을 수행할 경우 자료간 상관정도에 따라 예측 강우가 원자료보다 매우 크게 나타날 수 있음을 알 수 있다. 따라서 자료의 이러한 특성을 고려하여 단순크리깅을 수행한다면 향후 보다 정량적인 강우장을 추정할 수 있을 것으로 판단된다.
4. 결론
본 연구에서는 정량적 강우장을 추정하는데 있어, 강우 자료의 비정규성이 단순크리깅에 미치는 영향을 평가하였다. 이를 위해 먼저 정규분포를 따르지 않는 두 종류의 자료를 생성하였다. 한 자료는 비정규성이 약하게 나타난 자료이고, 다른 자료는 극단적인 값을 포함하여 비정규성이 강하게 나타난 자료이다. 본 연구에서는 각 자료의 정규성과 비정규성을 가정한 경우에 베리오그램을 유도하였다. 특히, 정규분포를 따르지 않는 자료에 정규성을 가정할 때 베리오그램 유도에 미치는 영향을 평가하였다. 또한 결정된 베리오그램을 이용하여 단순크리깅을 수행한 후 원자료의 분포와 비교하여 자료의 비정규성이 단순크리깅에 미치는 영향을 분석하였다. 마지막으로 관악산 레이더 강우 자료를 이용하여 위 과정을 반복하고 그 결과를 평가하였다. 연구를 통해 얻은 결과를 정리하면 다음과 같다.
1) 정규분포를 따르지 않는 자료에 정규성을 가정할 경우, 가우스모형으로 원자료의 특성에 적합한 문턱값과 상관거리를 갖는 베리오그램을 결정하기 어려운 것으로 나타났다. 이는 정규분포를 따르지 않는 자료의 베리오그램은 지수함수의 형태로 나타나 S 곡선의 양상을 보이는 가우스모형으로 적합하게 나타낼 수 없기 때문이다.
2) 모의자료를 이용한 분석에서는 극단적인 값이 포함되지 않은 자료의 경우 정규성을 가정한 단순크리깅 결과가 양호하게 나타날 수 있음을 확인하였다. 반면, 극단적인 값이 포함된 자료의 경우 비정규성을 가정한 단순크리깅 결과가 더 우수하게 나타났다. 그러나 이 경우에는 자료간 상관정도가 크면 단순크리깅 예측 결과가 원자료보다 크게 생성될 수 있는 것으로 나타났다. 이러한 결과는 검정통계량 분석에서도 유사하게 나타났다.
3) 레이더 강우 자료를 이용한 분석에서는 자료의 비정규성을 가정하여 단순크리깅을 수행한 경우가 정규성을 가정한 경우보다 적합한 결과를 생성하는 것으로 나타났다. 이 경우 원자료와 모의된 자료의 검정통계량을 평가한 결과에서도 동일한 결과를 제시하였다. 그러나 레이더 강우의 비정규성을 가정하여 단순크리깅을 수행할 경우 모의자료의 분석처럼 자료간 상관정도에 따라 예측 강우가 원자료보다 크게 생성될 수 있는 것으로 나타났다.
상기와 같은 결과는 모의자료와 레이더 강우 자료를 이용한 분석에서 잘 확인할 수 있었다. 그러나 실제 강우 자료가 갖고 있는 간헐성과 비등방성의 문제를 추가로 고려한다면 크리깅 예측 강우는 다르게 나타날 수 있을 것이다. 따라서 향후, 강우 자료가 가지는 이러한 특성을 모두 고려하여 크리깅을 적용할 수 있다면, 정량적인 크리깅 강우장을 생성할 수 있을 것으로 기대한다.
감사의 글
본 연구는 국토교통부 물관리연구사업의 연구비지원 (16AWMP-B079625-03)에 의해 수행되었습니다.