1. мДЬл°†
мµЬкЈЉ кЄ∞нЫДл≥АнЩФмЩА лПДмЛЬнЩФ нШДмГБмЬЉл°Ь нЩНмИШмЛЬ мє®мИШнФЉнХік∞А к∞Ам§СлРШк≥† мЮИлЛ§. лєЧлђЉнОМнФДмЮ• л∞П мІАнХШк≥µк∞Д м†Ал•Шм°∞ лУ±мЭШ мИШл∞©мЛЬмД§ м¶ЭлМАмЭШ нХДмЪФмД±мЭі м†ЬкЄ∞лРШк≥† мЮИлЛ§. лЛ§л•Є нХЬнОЄмЬЉл°ЬлКФ мЪ∞мИШкіАк±∞мЭШ л∞∞мИШлʕ놕 л∞П нЪ®мЬ®мЧР лМАнХЬ лђЄм†Ьм†РмЭі лґАк∞БлРШл©імДЬ мЪ∞мИШкіАк±∞ мЛЬмК§нЕЬмЭД мД§к≥ДнХШлКФ к≥Љм†ХмЧР к≥†л†§нХімХЉнХ† кЄ∞м°імЭШ лЛ§мЦСнХЬ к≤љнЧШмЛЭлУ§мЭі кіАк±∞мЛЬмК§нЕЬ лВілґАмЧРмДЬ л∞ЬмГЭнХШлКФ нЭРл¶ДнКємД±мЭД м†Бм†ИнЮИ л∞ШмШБнХШк≥† мЮИмІА л™їнХШлЛ§лКФ мЭШк≤ђмЭі м†ЬмЛЬлРШк≥† мЮИлЛ§. мЪ∞мИШкіАк±∞мЭШ к≥ДнЪН л∞П мД§к≥ДмЧР мЮИмЦі м§СмЪФ к≥†л†§мВђнХ≠ м§С нХШлВШлКФ кіАлВіл°Ь мЬ†мЮЕлРШлКФ нЖ†мВђ л∞П мє®м†ДлђЉмЭШ нЗім†БмЭД л∞©мІАнХШлКФ к≤ГмЭілЛ§. кіАк±∞лВі мє®м†ДлђЉмЭШ л∞©мІАл•Љ мЬДнХі нЩШк≤љлґА нХШмИШлПДмЛЬмД§кЄ∞м§А(2011)мЧРмДЬлКФ м†Бм†ХмЬ†мЖНмЭШ л≤ФмЬДл•Љ м†ЬмЛЬнХШк≥† мЮИмЬЉлВШ кіАк±∞мЭШ кµђм°∞м†Б мХИм†ХмД±мЧР міИм†РмЭі лІЮмґФмЦім†Є мЮИк≥† мЛ§м†Ьл°Ь кіАк±∞мЭШ кЄ∞лК•мГБ м§СмЪФ кЄ∞лК•мЭЄ нЖµмИШлК• лґАм°±мЭД к≥†л†§нХЬ лђЄм†Ьм†РмЭА лЛ§мЖМ к≤∞мЧђлРШмЦі мЮИлЛ§. мЬ†мЮЕмЬ†лЯЙмЧР лЛ§лЯЙмЭШ нЖ†мВђк∞А нПђнХ®лРШмЦі мЬ†мЮЕлР† к≤љмЪ∞ мЪ∞мИШкіАк±∞ мЛЬмК§нЕЬмЭШ мИШл¶ђнХЩм†Б мД§к≥ДмЧР мШБнЦ•мЭД лѓЄм≥Р мЬ†мґЬлЯЙк≥Љ нЖ†мВђлЯЙмЭД мЫРнЩЬнЮИ л∞∞мґЬмЛЬнВ§мІА л™їнХШк≤М лРЬлЛ§. нЖµмИШлґИлК• лђЄм†Ьл•Љ мХЉкЄ∞мЛЬнВ§л©∞ кіАлВі нЗім†БмЧР лФ∞л•Є лВімИШмє®мИШ л∞ЬмГЭ лђЄм†ЬмЧР м†Бм†ИнЮИ лМАмЭСнХШмІА л™їнХШк≤М лРЬлЛ§. лПДмЛђмІАмЧРмДЬ л∞ЬмГЭнХШлКФ нЖ†мВђмЮђнХілКФ нЖ†мВђ мЮРм≤імЧР кЄ∞мЭЄнХШлКФ 1м∞®м†Б мЮђнХі л∞ЬмГЭк≥Љ нХ®кїШ кЄ∞м°і л∞∞мИШмЛЬмД§ м≤ік≥ДмЭШ кЄ∞лК• мГБмЛ§мЭілЭЉлКФ лґАмИШм†БмЭЄ 2м∞®м†Б мЮђнХі л∞ЬмГЭмЭД мЬ†л∞ЬнХШлКФ нКємІХмЭД к∞ЦлКФлЛ§. лПДмЛђмІА нЖ†мВђмЮђнХі л∞ЬмГЭ мЛЬ л∞∞мИШмЛЬмД§мЭШ мЫРнЩЬнХЬ нЖµмИШлʕ놕 нЩХл≥і кЄ∞мИ†мЭі нХДмЪФнХШлЛ§к≥† нМРлЛ®лРЬлЛ§.
нХШм≤ЬмЭШ к≤љмЪ∞ лЛ§мЦСнХЬ кіАмЄ°мЮРл£Мл•Љ л∞ФнГХмЬЉл°Ь нЖµмИШлК• лґДмДЭмЭі к∞АлК•нХШл©∞ мИШл¶ђ лІ§к∞Ьл≥АмИШмЭШ мШБнЦ•л≤ФмЬДмЭШ мґФм†ХмЭі к∞АлК•нХШлЛ§. нЗім†Бк≥Љ кіА놮нХЬ мД†нЦЙ мЧ∞кµђлУ§мЭА лМАлґАлґД нХШмГБмЭД кЄ∞м§АмЬЉл°Ь мЮРл£МмИШмІС л∞П лґДмДЭмЭі мЭіл£®мЦім†Є мє®к∞ХмЖНлПДк∞А нЖ†мВђк∞А нЭШлЯђк∞АлКФ мЭімЖ°мЭШ к∞ЬлЕРмЬЉл°ЬлІМ мВђмЪ©лРШмЦімЩФлЛ§. нХШмІАлІМ лЛђл¶ђ мГЭк∞БнХіл≥іл©і мє®к∞ХмЖНлПДлКФ мЬ†мЮЕлРШлКФ нЖ†мВђмЭШ нКємД±мЭі л™®лСР к∞ЩмЭД мИШ мЧЖлЛ§. к≤∞кµ≠ нКємД±л≥Дл°Ь к∞Ал≥Ам†БмЭЄ к∞ТмЭД лЭДмЦімХЉ нХ®мЭі лІИлХЕнХШк≥† мЭімЧР лФ∞л•Є мє®к∞ХмЖНлПД мЧ≠мЛЬ мЭЉкіАлРЬ нХШлВШмЭШ к∞ТмЬЉл°ЬлІМ м†БмЪ©нХімДЬлКФ мЪ∞мИШкіАк±∞ лВі мЭімЖ°вЛЕмє®м†Д л∞П нЗім†БмЭШ нШДмГБмЭД л∞ШмШБнХШкЄ∞лКФ мЙљмІА мХКлЛ§. кЈЄлЯђлВШ лПДмЛЬмЬ†мЧ≠мЧРмДЬмЭШ мЪ∞мИШкіАл°Ьл•Љ нЖµнХЬ нЖ†мВђмЭШ мЭімЖ°к≥Љ мє®м†ДмЧР лМАнХЬ мЛ§мЄ°мЮРл£МлКФ кµ≠лВігГїмЩЄм†БмЬЉл°Ь к±∞мЭШ м†ДлђінХЬ мГБнГЬмЭіл©∞, мЭілКФ кіАл°Ь лВімЧРмДЬмЭШ лѓЄмДЄнХЬ нЖ†мВђ нЭРл¶ДмЧР лМАнХЬ кіАмЄ°мГБмЭШ мֳ놧мЫАмЧР мЫРмЭЄмЭі мЮИлЛ§.
кіАл°Ь лВі мЪ∞мИШмЭШ нЭРл¶ДлњРлІМ мХДлЛИлЭЉ лЛ§мЦСнХЬ нЭРл¶Д мГБнГЬмЧРмДЬмЭШ нЖ†мВђмЭШ нЭРл¶ДмЧР лМАнХЬ мЛ§нЧШм†Б кіАмЄ° лШРнХЬ лІ§мЪ∞ мֳ놧мЪі мЭЉмЭілЛ§. кіАк±∞ лВімЧРмДЬлКФ мЭімЖ°вЛЕмє®м†ДнШДмГБ л∞П нЗім†БмЭі мЭЉмЦілВ®мЧР лФ∞лЭЉ кіАк±∞мЭШ нЖµмИШлЛ®л©імЭі л≥АнХШлКФ л≥µмЮ°нХЬ нШДмГБмЭі л∞ЬмГЭнХЬлЛ§. мЪ∞мИШкіАк±∞мЭШ м†Бм†Х мД§к≥ДмЩА нЪ®мЬ®м†Б мЬ†мІАкіАл¶ђл•Љ мЬДнХімДЬлКФ кіАлВімЧРмДЬ л∞ЬмГЭнХШлКФ л≥µмЮ°нХЬ нШДмГБмЧР лМАнХі нЩХмЭЄмЭі нХДмЪФнХШл©∞, мЭіл•Љ л∞ФнГХмЬЉл°Ь м†Бм†Х нЖµмИШлК•мЭШ нЩХл≥іл•Љ мЬДнХЬ мЧ∞кµђк∞А нХДмЪФнХШлЛ§.
мИШмєШнХімДЭ л™®нШХмЭД мЭімЪ©нХШмЧђ кіАк±∞мЭШ нЖµмИШлК•мЭД к≤АнЖ†нХЬ мЧ∞кµђлУ§мЭД мВінОіл≥іл©і
Kim et al.(2014)мЭі мИШмєШнХімДЭ л™®нШХмЭД мЭімЪ©нХШмЧђ лМАмЛђлПД л∞∞мИШнД∞лДР мЬ†мЮЕлґАмЭШ нЖµмИШлʕ놕мЭД к≤АнЖ†нХШмШАлЛ§.
Choi and Lee(2016)лКФ лМАкЈЬл™® мЪ∞мИШкіАл°Ь лВілґАмЧРмДЬ л∞ЬмГЭнХ† мИШ мЮИлКФ Gerser нШДмГБмЧР лМАнХі л™®мЭШнХШмШАлЛ§. лСР мЧ∞кµђлУ§мЭШ к≤љмЪ∞ кіАк±∞ мД§к≥ДмЛЬ м†БмЪ© лІ§к∞Ьл≥АмИШлУ§мЧР лМАнХЬ к≤∞к≥ЉлУ§мЭД л∞ФнГХмЬЉл°Ь мЪ∞мИШкіАк±∞ мЛЬмК§нЕЬмЭШ мХИм†Хм†БмЭЄ мД§к≥Дл∞©мХИмЭД м†ЬмЛЬнХШмШАлЛ§. кЈЄлЯђлВШ мЬ†мЮЕлРШлКФ мє®м†ДлђЉмЧР лМАнХЬ к≥†л†§лКФ л∞ШмШБнХШмІА мХКмХШмЬЉл©∞ к≥µкЄ∞мХХ놕 лУ±мЭД к≥†л†§нХЬ мИЬмИШмЬ†лЯЙмЭШ л∞∞м†Ьлʕ놕мЭД м§СмЛђмЬЉл°Ь мЧ∞кµђк∞А мЭіл£®мЦі м°МлЛ§.
мЭЉл∞Шм†БмЬЉл°Ь мЪ∞мИШкіАк±∞л°Ь мЬ†мЮЕлРШлКФ мє®м†ДлђЉмЭШ лґАнХШлЯЙ м†ХлПДлКФ к∞ХмЪ∞мЭШ нШХнГЬмЧР лФ∞лЭЉ лВШлЙШлКФлН∞, нХілЛє к∞ХмЪ∞к∞А к∞ЦлКФ нКємІХмЧР лФ∞лЭЉ мЬ†лЯЙмЭШ л≥АлПЩмЭі лЛ§л•ік≥† мЭімЧР лФ∞л•Є мЪ∞мИШмЬ†мґЬмИШмЩА лПЩл∞ШнХШлКФ мє®м†ДлђЉмЭШ нКємД± лШРнХЬ м†ДнША лЛ§л•Є нКємІХмЭД к∞ЦлКФлЛ§(
Ashley et al., 2004). мІАнСЬл©імЬЉл°ЬлґАнД∞ нШХмД±лРШмЦі мӪ놧 лУ§мЦімШ® лЛ§лЯЙмЭШ к∞АлКФ мЮЕмЮРлУ§мЭА к∞ХмЪ∞мВђмГБмЭШ мЛЬмЮСк≥Љ лПЩмЛЬмЧР мӪ놧 л³놧мЩА мЪ∞мИШкіАк±∞л°Ь мЬ†мЮЕлРШк≥† мЭілКФ лґАмЬ†мВђлЯЙмЭілЭЉлКФ мЭіл¶ДмЬЉл°Ь мЬ†мЮЕлЯЙ лВімЧРмДЬ мІЩмЭА лЖНлПДмЄµмЭД нШХмД±нХЬлЛ§.
мЪ∞мИШкіАк±∞л°Ь мЬ†мЮЕлРШлКФ нЖ†мВђмЭШ мИШлђЄнХЩм†Б нЭ°мИШмЪ©лЯЙ(Flood Absorption Capacity)мЭА л≥інЖµ мЮЕмЮРмЭШ нБђкЄ∞мЧР лФ∞лЭЉ нШДм†АнХШк≤М лЛђлЭЉмІАлКФ к≤љнЦ•мД±мЭД к∞ЦлКФлЛ§. лѓЄмДЄнХЬ мЮСмЭА мЮЕмЮРлУ§мЭШ к≤љмЪ∞ нХілЛє мЮЕмЮРлУ§мЭі к∞ЦлКФ нСЬл©ім†БмЧР лєДнХі лЛ®мЬД м§СлЯЙлЛє лЖТмЭА нЭ°мИШлК•мЭД к∞Цк≥† мЭімЧР лФ∞л•Є мЬ†мЮЕлРШлКФ лєДмЬ®мЭі мї§ нЖ†мВђмЭШ лєДмЬ®мЭі лЖТмЭА лЖНлПДмЄµмЭД нШХмД±нХШк≤М лРЬлЛ§.
мЪ∞мИШкіАк±∞л°Ь мЬ†мЮЕлРШлКФ нЖ†мВђ мЮЕмЮРлУ§мЭШ нБђкЄ∞мЩА кіА놮лРЬ мЧ∞кµђлУ§мЭД мВінОіл≥іл©і
Chebbo and Bachoc(1992)лКФ мЪ∞мИШкіАк±∞ мЛЬмК§нЕЬмЬЉл°Ь мЬ†мЮЕлРШлКФ міЭ лґАмЬ†мВђлЯЙ(Total Suspended Solid, TSS)мЭШ 68вИЉ85%к∞А 100ќЉm лѓЄлІМмЭШ мЮЕмЮР мІБк≤љмЭД к∞ЦлКФлЛ§к≥† м†ХмЭШнЦИлЛ§.
Bertrand-Krajewski et al.(2008)мЭШ к≤љмЪ∞ лПЩмЭЉнХЬ л∞©л≤ХмЬЉл°Ь 64вИЉ92ќЉmмЭШ л≤ФмЬДл•Љ к∞ЦлКФлЛ§к≥† м†ЬмХИнХШмШАлЛ§.
Becouze and Lareure(2016)лКФ мЪ∞мИШкіАк±∞л°Ь мЬ†мЮЕлРШлКФ нЖ†мВђлУ§мЭШ мІБк≤љ лєДмЬ®мЭД к∞Бк∞БмЭШ мЛ§м†Ь к∞ХмЪ∞мВђмГБмЬЉл°ЬлґАнД∞ м°∞мВђнХШмШАлКФлН∞ нПЙкЈ†м†БмЬЉл°Ь 85-117ќЉmмЬЉл°Ь мХЮмДЬ мЦЄкЄЙнХЬ лЕЉлђЄк≥Љ лМАлЮµ 7-17ќЉmм†ХлПД м∞®мЭіл•Љ л≥імШАлЛ§.
мЬДмЧРмДЬ лґАмЬ†мВђлЯЙк≥Љ мЬ†мЮЕ мІБк≤љмЭШ нБђкЄ∞л•Љ м°∞мВђнХЬ лЕЉлђЄлУ§мЭШ к≥µнЖµм†РмЭА к≤∞кµ≠ мЪ∞мИШкіАк±∞л°Ь мЬ†мЮЕлРШлКФ нЖ†мВђлЯЙмЭА лґАмЬ†мВђмЩА мЭіл•Љ нПђнХ®нХШлКФ мЮСмЭА мЮЕк≤љлУ§л°Ь лМАлґАлґД кµђмД±лРШмЦі мЮИмЬЉл©∞, нХілЛє мЮЕк≤љмЭШ лєДмЬ®мЭА мЬ†мґЬмЭі л∞ЬмГЭнХШлКФ мЬ†мЧ≠к≥Љ к∞ХмЪ∞мЭШ нКємД±мЧР лФ∞лЭЉ м†Ьк∞Бк∞БмЭілЭЉлКФ к≤ГмЭілЛ§.
л≥Є мЧ∞кµђмЧРмДЬлКФ к∞ХмЪ∞мЛЬ мЬ†мґЬлЯЙк≥Љ лНФлґИмЦі лЛ§лЯЙмЭШ нЖ†мВђк∞А мЬ†мЮЕлРШлКФ мЪ∞мИШкіАк±∞л•Љ м†ДмВ∞ мЬ†м≤імЧ≠нХЩм†Б л™®мВђл•Љ нЖµнХімДЬ кіАк±∞ лВілґАмЭШ нЗім†БнКємД±мЭД л™®мЭШнХШмШАлЛ§. л≥ілЛ§ м†ХнЩХнХЬ мЬ†лПЩнХімДЭмЭД мЬДнХШмЧђ лґАмИШм†БмЭЄ л™®мЭШлУ§мЭД м†ЬмЩЄнХШк≥† лЛ®кіАнШХнГЬл°Ь кµђм≤інЩФнХШмЧђ нХімДЭмЛЬк∞ДмЭД м§ДмЭЄ мД§к≥Д л™®лНЄмЭД м†БмЪ©нХШмШАлЛ§. лґДмДЭмЧРлКФ CFD л™®нШХмЭШ SolverлУ§ м§С Ansys Fluent л™®нШХмЭД м†БмЪ©нХШмШАлЛ§. мЭі л™®нШХмЭА м£Љл°Ь кЄ∞к≥Д л∞П мВ∞мЧЕ к≥µнХЩмЭШ лґДмХЉмЭШ мЛ§лђімЩА нХЩмИ† мЧ∞кµђл•Љ лєДл°ѓнХЬ мЧђлЯђлґДмХЉмЧР к±Єм≥Р к∞АмЮ• лДРл¶ђ мВђмЪ©лРШлКФ мГБмЪ© CFD Solver м§С нХШлВШмЭілЛ§. лНФлґИмЦі нХілЛє л™®нШХмЭА мЪ∞мИШкіАк±∞л•Љ лєДл°ѓнХЬ мИШмєШнХімДЭмЧРлПД лСРл£® м†БмЪ©лРШк≥† мЮИлКФлН∞ лМАнСЬм†БмЬЉл°Ь
Stovin(1996),
Lipeme Kouyi(2004) лУ±мЭі CFD л™®нШХмЭД мЭімЪ©нХШмЧђ лПДмЛђмІА мЪ∞мИШкіАк±∞ мЛЬмК§нЕЬмЭШ лЛ§мЦСнХЬ мХХ놕л•Ш нЭРл¶Д л∞П нЕМмК§нКЄл≤†лУЬмЭШ м†БмЪ©мЭД нЖ†лМАл°Ь лПДмЮЕнХШкЄ∞ мЛЬмЮСнЦИлЛ§. лґДмДЭмЭД мЬДнХЬ мДЄлґАм°∞к±імЭШ к≤љмЪ∞ к≤љмВђк∞А мЧЖлКФ кіАк±∞м°∞к±імЭД кЄ∞м§АмЬЉл°Ь к≤љмВђлПД м°∞к±імЭД л≥АнЩФмЛЬмЉЬк∞Ал©∞ кіАк±∞ лВілґАмЧРмДЬ л∞ЬмГЭнХШлКФ нЗім†БнКємД±мЭД кµђм≤ім†БмЬЉл°Ь лґДмДЭнХШмШАлЛ§. мЪ∞мИШкіАк±∞лВі нЭРл¶ДмЭД л™®мЭШнХШкЄ∞ мЬДнХШмЧђ нЖµмИШлʕ놕мЭД нПЙк∞АнХШмШАмЬЉл©∞, м†Бм†Х мЬ†мЖНл≤ФмЬД лВімЧРмДЬ нЖµмИШлʕ놕 к≤АнЖ† л∞П мШИмГБ нЗім†БлЯЙ мґФм†ХмЛЭмЭД м†ЬмХИнХШмШАлЛ§.
2. мИШмєШл™®нШХ л∞©л≤Х л∞П мЛЬлЃђл†ИмЭімЕШ м°∞к±і
мИШмєШнХімДЭ л™®лНЄлІБмЭШ л™©м†БмЭА мЭЉл∞Шм†БмЬЉл°Ь лЛ®мГБ мЬ†м≤інЭРл¶Д(Single Phase Fluid Flow) л∞П лЛ§мГБ мЬ†м≤інЭРл¶Д(Multiphase Phase Fluid Flow) лґДмДЭмЧР лМАнХЬ мИШнХЩм†Б л™®лНЄмЭД м¶Эл™ЕнХШлКФлН∞ мЮИлЛ§. л≥Є мЧ∞кµђмЧРмДЬ CFD л™®нШХмЭД мЭімЪ©нХЬ лґДмДЭмЭД мІДнЦЙнХЬ мЭімЬ†лКФ кЄ∞м°і мЪ∞мИШкіАк±∞ лВі нЖ†мВђмЭШ мЭімЖ°вЛЕмє®м†ДмЭД л™®мЭШнХШлКФ мЬ†мґЬнХімДЭ л™®нШХмЭШ к∞ЬмД†мЧР мЮИмЦі мГБнШЄ л≥імЩДм†БмЭЄ мЧ≠нХ†мЭД мИШнЦЙнХШл©∞, лђЄм†Ьк∞А л∞ЬмГЭнХШлКФ м£ЉмЪФ нЗім†Бкµђк∞ДмЭД л∞ФнГХмЬЉл°Ь кµ≠лґАмШБмЧ≠мЧР лМАнХЬ мГБмДЄнХЬ нХімДЭ л∞П к≤∞к≥Љ лПДмґЬмЭі к∞АлК•нХШлЛ§к≥† нМРлЛ®лРШмЧИлЛ§.
CFD нХімДЭмЧР мЮИмЦі л™®лУ† лђЄм†ЬлКФ міИкЄ∞м°∞к±ік≥Љ к≤љк≥Д м°∞к±імЭШ кіАм†РмЭД м†ХмЭШнХШлКФ к≤ГмЭі к∞АмЮ• м§СмЪФнХШлЛ§. мВђмЪ©мЮРк∞А м†ХнЩХнХШк≤М лґДмДЭнХШк≥†мЮР нХШлКФ л™®лНЄмЭД мІАм†ХнХШк≥† мЭімЧР м†БнХ©нХЬ мИШмєШл™®лНЄмЭД кµђнШДнХШмЧђ мШђл∞Фл•Є мЧ∞мВ∞к≥Љм†ХмЭД нЖµнХі нХіл•Љ нТАмЦілВШк∞АлКФ к≤ГмЭі м§СмЪФнХШлЛ§. нКєнЮИ лґАм†Хл•Ш л∞П лВЬл•ШнЭРл¶ДмЭШ лђЄм†ЬмЧР мЮИмЦімДЬлКФ лґДмДЭмЧР м†БмЪ©лРШлКФ л™®лУ† л≥АмИШлУ§мЭі міИкЄ∞ к∞Тк≥Љ лЛђл¶ђ м†Дл∞Шм†БмЭЄ нЭРл¶ДмШБмЧ≠мЧРмДЬ лЛ§мЦСнХЬ к∞ТмЭД лЭДк≤М лРШлѓАл°Ь мЭімЧР лФ∞л•Є л≤ФмЬДл•Љ м†ЬнХЬнХШлКФ к≤Г лШРнХЬ м§СмЪФнХЬ л≥АмИШл°Ь л∞ШмШБлРШмЦімХЉ нХЬлЛ§(
Versteeg and Malalasekera, 2007).
л≥Є мЧ∞кµђмЧРмДЬлКФ кіАк±∞ лВілґАмЭШ нЗім†БлЯЙмЭД м§ДмЭік≥† нЖµмИШлК• к∞ЬмД†мЭД л™©нСЬл°Ь нХШл©∞ мЭіл•Љ мЬДнХі л≥ілЛ§ м†ХнЩХнХЬ мЬ†лПЩнХімДЭмЭД мЬДнХШмЧђ лґАмИШм†БмЭЄ л™®мЭШлУ§мЭД м†ЬмЩЄнХШк≥† лЛ®кіАнШХнГЬл°Ь кµђм≤інЩФнХШмЧђ нХімДЭмЛЬк∞ДмЭД м§ДмЭЄ лЛ®нОЄ мД§к≥Д л™®лНЄмЭД мВђмЪ©нХШмШАлЛ§. мИШмєШл™®мЭШлКФ мЪ∞мИШкіАк±∞мЭШ нШХмГБк≥Љ мДЄлґА мЛЬмД§лђЉлУ§мЭШ м†Сл™© нШХнГЬл•Љ к≥†л†§нХШмЧђ 2м∞®мЫР л™®мЭШл°Ь мИШнЦЙлРШмЧИмЬЉл©∞, 0.6m√Ч10m(мЫРнШХкіАк±∞)мЭШ мШБмЧ≠мЧР лМАнХШмЧђ мХљ 140,000к∞ЬмЭШ мВђк∞БнШХ к≤©мЮРлІЭмЭД кµђмД±нХШмШАлЛ§. к≥ДмВ∞ мЛЬк∞Д к∞Дк≤©(Time Interval)мЭА вИЖt=1міИл•Љ м†БмЪ©нХШмЧђ м†Дм≤і 500міИкєМмІА к≥ДмВ∞мЭД мИШнЦЙнХШмШАмЬЉл©∞, к∞Бк∞БмЭШ мЛЬк∞Д к∞Дк≤©мЧРмДЬ 10нЪМмЭШ лВілґА к≥ДмВ∞(step length factor)мЭД л∞Шл≥µнХШлПДл°Э мД§м†ХнХШмШАлЛ§.
мЛЬлЃђл†ИмЭімЕШ м°∞к±імЭШ к≤љмЪ∞ нЖ†мВђмЩА мЬ†м≤імЭШ мЬ†мЮЕмЬ†мЖНмЭД 1m/s, 2m/s, 3m/s м°∞к±імЧРмДЬ мЬ†м≤ілВі нЖ†мВђмЭШ нШЉмЮЕлЖНлПДл•Љ 10%, 30%, 50%мЧР лМАнХШмЧђ к≥†л†§нХШмШАлЛ§. мЭілХМ лУ§мЦімШ§лКФ мЬ†мЮЕ нЖ†мВђмЭШ мІБк≤љмЭА к∞Б м°∞к±імЧР 1.0mm, 3.0mm, 5.0mmл°Ь м†БмЪ©нХШмШАмЬЉл©∞, мХЮмДЬ мЦЄкЄЙнХЬ м°∞к±ілУ§мЭД кіАк±∞к≤љмВђ 0¬∞, 1¬∞, 3¬∞, 5¬∞мЧР м†БмЪ©нХ®мЬЉл°ЬмН® міЭ 108к∞АмІАмЭШ мЛЬлЃђл†ИмЭімЕШ м°∞к±імЧР лМАнХі лґДмДЭмЭД мІДнЦЙнХШмШАлЛ§.
2.1 нХімДЭл™®лНЄ
нЖ†мВђк∞А мЬ†мЮЕлРШлКФ кіАк±∞ лВілґАмЭШ лВЬл•Ш нЪ®к≥Љл•Љ нХімДЭнХШкЄ∞ мЬДнХімДЬлКФ лВЬл•Ш нШДмГБ л∞П лВЬл•Шл™®лНЄмЧР лМАнХЬ к≥†л†§к∞А нХДмЪФнХШлЛ§. мЬ†м≤ік∞А мІАмЖНм†БмЬЉл°Ь к±∞лПЩнХ† лХМмЧРлКФ мДЬл°Ь мЭімЫГнХЬ мЬ†м≤імЭШ мЄµл•Ш м†Рмı놕мЧР мЭШнХЬ м†Длˮ놕мЭі мЬ†м≤імЭШ кµђлПЩ놕мЭі лРШмЦі к≤∞кµ≠ мЭЉм†ХнХЬ мЄµмЭД мЭіл£®мЦі нЭРл•ілКФ мЄµл•Ш мЬ†лПЩмЭі лВШнГАлВЬлЛ§. нХШмІАлІМ мЬ†мЖНмЭі м¶Эк∞АнХШмЧђ м†ДлЛ®мЭС놕мЭі лІ§мЪ∞ к∞ХнХімІАл©і к≤∞кµ≠ м†Рмı놕мЧР мЭШнХЬ м†ДлЛђлІМмЬЉл°ЬлКФ мЭіл•Љ к∞РлЛєнХШмІА л™їнХШмЧђ м†ДлЛ®мЭС놕мЭА мХДм£Љ мЮСмЭА лВЬл•ШмЩА(Turbulent Eddy)лУ§л°Ь кє®мЦімІАк≤М лРШк≥† мЭімЧР мЭШнХШмЧђ м†ДлЛ®мЭС놕мЭА мЬ†м≤і лВілґАл°Ь м†ДлЛђлРЬлЛ§. мЬ†мЖНмЭі м¶Эк∞А нХ†мИШл°Э лВЬл•ШмЩАмЭШ нБђкЄ∞лКФ м†Рм†Р мЮСмХДмІАк≥† мЬ†м≤імЭШ к±∞лПЩмЭА мЛЬк∞ДмЭШ л≥АнЩФмЧР лФ∞лЭЉ нБђк≤М л≥АнХШк≤М лРЬлЛ§. мЭілХМ мЬ†лПЩмЧРлКФ мЭЉм†Х нШХмЛЭмЬЉл°Ь л≥АнЩФнХШлКФ мЛЬк∞Д нПЙкЈ†к∞Тк≥Љ мІІмЭА мЛЬк∞Дм£ЉкЄ∞л•Љ к∞ЦлКФ мЪФлПЩ(Fluctuation)к∞ТмЭі м°імЮђнХШк≤М лРШлКФлН∞ мЭілЯђнХЬ мЬ†лПЩмЭД лВЬл•Ш мЬ†лПЩмЭілЭЉ нХЬлЛ§.
к≥†м≤імЮЕмЮРмЭЄ нЖ†мВђлЯЙк≥Љ мЬ†м≤іл°Ь кµђмД±лРЬ мЬ†мЮЕлЯЙмЭД нХімДЭнХШкЄ∞ мЬДнХімДЬлКФ лЛ§мГБ мЬ†м≤і нЭРл¶Д лґДмДЭмЭі нХДмЪФнХШлЛ§. л≥Є мЧ∞кµђмЧРмДЬлКФ лЛ§мГБ мЬ†м≤і лґДмДЭл™®лНЄ м§С Eulerian-Eulerian л™®лНЄмЭД м†БмЪ©нХШмШАмЬЉл©∞, мЧ∞мЖНл∞©м†ХмЛЭк≥Љ лВЬл•Ш мЪілПЩмЭД нХімДЭнХШкЄ∞ мЬДнХімДЬлКФ k-ќµл™®лНЄмЭД мВђмЪ©нХШмШАлЛ§. kлКФ лђЉл¶ђм†БмЬЉл°Ь лВЬл•ШмЪілПЩмЧРлДИмІАл•Љ мЭШлѓЄнХШл©∞ лВЬл•ШмД≠лПЩмЖНлПДл°Ь м†ХмЭШлРШк≥†, лВЬл•Ш мЖМмВ∞мЬ®мЭД м†ХмЭШнХШлКФлН∞ мВђмЪ©лРЬлЛ§. k-ќµл™®лНЄмЭА мХЮмДЬ мЦЄкЄЙнХЬ л∞ФмЩА к∞ЩмЭі Eddy Viscosity л™®лНЄл°Ь лЛ§мЭМмЛЭк≥Љ к∞ЩмЭі kмЩА ќµмЭД нЖµнХі ќЉtл•Љ мЦїмЭД мИШ мЮИлЛ§.
CќЉлКФ л™®лНЄмГБмИШл°Ь мЭЉл∞Шм†БмЬЉл°Ь 0.09 к∞ТмЭД мВђмЪ©нХЬлЛ§. кіАлВі нЗім†Б л∞ЬмГЭмЧР лФ∞л•Є кµ≠лґАм†БмЭЄ мШБмЧ≠мЧРмДЬ kмЩА ќµл•Љ мХДлЮШмЩА к∞ЩмЭА 2к∞ЬмЭШ л≥ДлПДмЭШ мИШмЖ°л∞©м†ХмЛЭ(k-equation, ќµ-equation)мЭД к≥ДмВ∞нХ®мЬЉл°ЬмДЬ лВЬл•ШмЭС놕мЭД л™®лНЄнХШк≤М лРЬлЛ§.
мЬДмЭШ л∞©м†ХмЛЭмЧРмДЬ лВШнГАлВШлКФ к∞Б к≥ДмИШлУ§мЭА Standard k-ќµ ModelмЧРмДЬ лЛ§мЭМк≥Љ к∞ЩмЭА к∞ТмЭі мВђмЪ©лРЬлЛ§.
k-ќµ л™®лНЄмЭА лВЬл•ШмЭШ мЛЬк∞Дм†БмЬЉл°Ь л≥АлПЩнХШлКФ мЖНлПДк∞А мЛЬк∞Д нПЙкЈ† мЖНлПДмЩА л≥АлПЩлґДмЭШ мЖНлПДл°Ь лВШлИМ мИШ мЮИлЛ§лКФ к∞Ам†Х нХШмЧР Navier Stokes л∞©м†ХмЛЭмЭД мЛЬк∞Д нПЙкЈ†нХШмЧђ мЖНлПД л≥АлПЩлЯЙмЭШ мГБкіА нХ≠мЭі мЭС놕 нШХнГЬмЭЄ л†ИмЭілЖАм¶И мЭС놕 нХ≠мЬЉл°Ь лВШнГАлВЄ к≤ГмЭілЛ§.
2.2 к≤љк≥Дм°∞к±і
л≥Є мЧ∞кµђмЧРмДЬ к≥†л†§нХімХЉнХ† к≤љк≥Дм°∞к±імЭА лІ§мЪ∞ лЛ§мЦСнХШл©∞ мЭілУ§ м§С мЛ§м†Ь лґДмДЭмЧР м†БмЪ©нХЬ м°∞к±імЭА нБђк≤М мЮЕкµђ, мґЬкµђ л∞П л≤љл©імЭШ к≤љк≥Дм°∞к±імЭілЛ§. мЮЕкµђмЭШ к≤љмЪ∞ мЬ†лПЩмЧР кіАнХЬ л™®лУ† м†Хл≥іл•Љ мХМк≥† мЮИлКФ мШБмЧ≠мЬЉл°Ь мВђмЪ©мЮРк∞А мЬ†мЖНмЭілВШ мХХ놕, нКємД±кЄЄмЭі, лВЬл•Шк∞ХлПД, мШ®лПД лУ±мЭД м†ХмЭШнХ† мИШ мЮИлЛ§. мґЬкµђлКФ мЬ†лПЩмЭШ л∞©нЦ•мЭі л™®лСР л∞Фкє•мЭД нЦ•нХ† лХМ мВђмЪ©нХ† мИШ мЮИмЬЉл©∞ мЬ†лПЩмЧР кіАнХЬ м†Хл≥ілКФ нХДмЪФл°Ь нХШмІА мХКлКФлЛ§.
л≥Є мЧ∞кµђмЧРмДЬлКФ мЬ†мЮЕ м°∞к±імЭі мЛЬк∞ДмЧР лФ∞лЭЉ л≥АнХШк±∞лВШ кЄ∞нГА нКємІХмЭі нШХмД±лРШмІА мХКлКФлЛ§к≥† к∞Ам†ХнХШмШАлЛ§. л∞ШлМАл°Ь мЬ†мґЬлРШлКФ нЭРл¶ДмЭД лЛ§мЦСнХШк≤М к∞Ам†ХнХ®мЬЉл°ЬмН® мЛ§м†ЬнШДмГБмЭД нПђкіДнХШлКФ л™®мВђнХ† мИШ мЮИлКФ мЮ•м†РмЭі мЮИлЛ§. к≥ДмВ∞мЛЬк∞Д лШРнХЬ лЛ®мґХлРШлѓАл°Ь л∞Шл≥µм†БмЭЄ к≥ДмВ∞мЭі к∞АлК•нХШлПДл°Э кµђмД±нХШмШАлЛ§. лґДмДЭ кµђк∞ДмЭШ к≤љк≥ДлКФ л≤љл©і л∞П мЬ†м≤імЭШ мЬ†вЛЕмґЬмЮЕкµђк∞А нХілЛєлРШлКФлН∞ л≤љл©імЭА лђілѓЄлБДлЯђмІР м°∞к±і(No Slip Condition)мЭД лґАмЧђнХШмШАлЛ§. лФ∞лЭЉмДЬ мЪ∞мИШкіАк±∞мЭШ мЬ†мЮЕкµђлКФ нЖ†мВђк∞А мЬ†лЯЙмЭі к∞Хм†Ьм†БмЬЉл°Ь мЬ†мЮЕлРШлКФ м°∞к±імЭілЭЉ нХ† мИШ мЮИк≥†, мЬ†мґЬкµђлКФ л∞©л•ШнКємД±мЭД к∞АмІД мЮРмЧ∞ мЬ†мґЬкµђ м°∞к±ік≥Љ к∞ЩлЛ§. мЬ†вЛЕмґЬмЮЕкµђмЭШ нШХмГБмЭі л≥µмЮ°нХШмІА мХКкЄ∞ лХМлђЄмЧР мЬ†мЮЕкµђлКФ мЖНлПД к≤љк≥Дм°∞к±імЭД мВђмЪ©нХ®мЭД мЫРмєЩмЬЉл°Ь нХШмШАк≥†, мЬ†мґЬкµђлКФ м∞®мХХ к≤љк≥Дм°∞к±імЭД мВђмЪ©нХШмЧђ мЬ†лЯЙмЭД л∞∞мґЬнХШлКФ кіАк≥Дл•Љ мД§м†ХнХШмШАлЛ§.
3. мИШмєШл™®нШХмЭД мЭімЪ©нХЬ кіАлВі нЗім†БнЖ†мВђлЯЙ мШИмЄ°
3.1 мИШмєШнХімДЭ л™®нШХмЭШ к≤Ам¶Э
мЭЉл∞Шм†БмЬЉл°Ь мИШмєШнХімДЭ л™®нШХмЭД мЭімЪ©нХЬ лґДмДЭмЭД мЬДнХімДЬлКФ лґДмДЭ мЭім†ДмЧР к≤Ам¶ЭлМАмГБмЭД л∞ФнГХмЬЉл°Ь кµђмґХнХШк≥†мЮР нХШлКФ л™®нШХмЭД мЬДнХЬ к≤Ам¶Эк≥Љм†ХмЭі нХДмИШм†БмЭілЛ§. л≥ЄлЮШмЭШ л™®нШХлІМмЭД к∞АмІАк≥† к≤Ам¶ЭмЭД нХ† к≤љмЪ∞, мЦілЦ†нХЬ м°∞к±ік≥Љ лґДмДЭнКємД±мЭі мГБмЭінХЬ к≤ГмЧР лМАнХімДЬ л™®лУ† м°∞к±імЭД к≤Ам¶ЭнХШлКФ к≥Љм†ХмЭА мЛЬк∞ДмЭі мШ§лЮШ к±Єл¶ђк≥† кЈЄлІМнБЉ кЈЄмЧР лМАнХЬ мШ§л•ШлУ§мЭД мЮ°мХДм§Д мݪ놕к≥Љ мЛЬк∞ДмЭі лЛ§мИШ мЖМл™®лРШмЦі лєДнЪ®мЬ®м†БмЭілЭЉ нМРлЛ®лРЬлЛ§.
л≥Є мЧ∞кµђмЧРмДЬлКФ к≤Ам¶ЭмЭД мЬДнХі кЄ∞м°імЧР м†ЬмЛЬлРЬ м£ЉмЪФ лЕЉлђЄмЭД л∞ФнГХмЬЉл°Ь кµђмґХнХЬ л™®нШХмЭД к≤Ам¶ЭнХШк≥†мЮР нХШмШАмЬЉл©∞ мЛ§нЧШм†БмЭЄ мЄ°л©імЧР мЮИмЦі мґХмЖМлРЬ л™®нШХмЭД лѓЄл¶ђ кµђлПЩмЛЬмЉЬ л≥ік≥† кЈЄ нЫДмЧР мШ§л•ШлУ§мЭД нХШлВШмФ© м∞ЊмХДлВімЦі л≥ЄлЮШмЭШ нКємД±мЭД л∞ШмШБнХШк≥†мЮР нХШмШАлЛ§. к≤Ам¶ЭмЭА
Tamer et al.(2014)мЭі м†ЬмЛЬнХЬ мЬ†м≤ік≥Љ нЖ†мВђмЭШ мЮЕк≤љ, л∞АлПД, кµђмД±лєД л∞П кіАк±∞мЭШ м†ЬмЫР, к≤љмВђлПД лУ±мЭД лПЩмЭЉнХШк≤М м†БмЪ©нХШмЧђ кµђмД±нХШк≥†мЮР нХШлКФ л™®нШХмЭШ к≤Ам¶ЭмЭД мІДнЦЙнХШмШАлЛ§.
лЛ§мЭМмЭШ нСЬлКФ л™®нШХмЭШ к≤Ам¶ЭмЭД мЬДнХі кµђмД±нХЬ мГБмДЄ м†ЬмЫРк≥Љ к≤Ам¶ЭмЧР м†БмЪ©лРЬ к∞Б м°∞к±ілУ§мЭД м†ЬмЛЬнХШмШАлЛ§.
Table 4 мЬДмЧР л™ЕмЛЬлРЬ м°∞к±ілУ§мЭД л∞ФнГХмЬЉл°Ь нХімДЭмЭД мИШнЦЙнХШлРШ, нХімДЭмЛЬк∞ДмЭШ к≤љмЪ∞ мЛ§м†Ь к∞ХмЭШ нМ®нДік≥Љ к∞ЩмЭі л≥АлПЩмД±мЭД м£ЉмІА мХКк≥†, мІІк≤М 10~20міИмЭШ мДЄлґДнЩФлРЬ мЛЬк∞Дк∞Дк≤©мЭД м†БмЪ©нХШмЧђ мЭімЖ°вЛЕмє®м†ДмЭШ нКємД±мЭД нЩХмЭЄнХШмШАлЛ§. м†ЬмЛЬлРЬ м°∞к±ілУ§к≥Љ к∞ЩмЭі 10%, 20%, 30%мЭШ лЖНлПД м°∞к±імЧР лМАнХШмЧђ 1вИЉ3m/sмЭШ мЬ†мЖНм°∞к±імЭД л∞ШмШБнХШмЧђ к≤Ам¶ЭмЭД мЛ§мЛЬнХШмШАлЛ§. лЛ§мЭМмЭШ
Figs.2мЩА
3мЭД л≥іл©і мЬ†мЮЕлРЬ нЖ†мВђмЩА мЬ†лЯЙмЭШ кіАк≥ДмЧРмДЬ 30% лЖНлПДмЧР лМАнХЬ к≤∞к≥Љк∞А мµЬміИ к≤Ам¶ЭмЭШ кЄ∞м§АмЭі лРЬ
Tamer et al.(2014)мЭШ к≤∞к≥ЉмЩА мЭЉмєШнХШлКФ к≤ГмЬЉл°Ь лВШнГАлВђлЛ§. мЬ†мЖНм°∞к±і мЧ≠мЛЬ к≤Ам¶ЭмЭШ кЄ∞м§АмЭі лРЬ лЕЉлђЄк≥Љ лПЩмЭЉнХЬ нШХнГЬмЭШ мґФмЭіл°Ь лВШнГАлВђмЬЉл©∞, мЛ§м†Ь кіАк±∞мЭШ нКємД±мГБ кіА мµЬлМАмІБк≤љмЭШ 80%мЧРмДЬ мЬ†мЖН л∞П мЬ†лЯЙмЭі мµЬлМАк∞А лРШлКФ м†РмЭД к∞РмХИнХ† лХМ л™®лНЄлІБмЭД нХШкЄ∞ мЬДнХЬ мµЬміИ лВЬл•Шл™®нШХмЭШ к≤Ам¶ЭмЭі лєДкµРм†Б мЮШ мЭіл£®мЦім°МлЛ§ нМРлЛ®лРЬлЛ§.
Table 1
Simulation Condition and Case
|
Inlet Velocity (m/s) |
Volume Fraction (%) |
Sand Diameter (mm) |
Pipe Gradient (°) |
Total Simulation Case |
|
1.0, 2.0, 3.0 |
10, 30, 50 |
1.0, 3.0, 5.0 |
0, 1, 3, 5 |
108 |
Table 2
Standard k-ќµ Model Patameters
|
CќЉ
|
Cќµ1
|
Cќµ2
|
ќіk
|
ќіќµ
|
|
вАГ0.09вАГ |
вАГ1.44вАГ |
вАГ1.92вАГ |
вАГ1.0вАГ |
вАГ1.3вАГ |
Table 3
Analysis Condition in FLUENT
|
Condition |
Setting |
|
Type |
Fluid |
|
Material |
Water |
|
Turbulence Model |
K вАУ ќµ Standard |
|
Inlet |
Velicity = 1.0~3.0m/sec |
|
Outlet |
вАГRelative Pressure = 0 (Pa)вАГ |
|
Wall Influence of Flow |
No Slip |
|
вАГSurface Influence of FlowвАГ |
Free Slip |
Table 4
Verification Conditions of the Modelling
|
Title |
Sand-water Transport |
|
Geometry |
6 m x 0.0268m |
|
Model |
Eulerian-Eulerian model, Turbulent flow |
|
вАГMixture boundary ConditionsвАГ |
Inlet Velocity: 3m/s Inlet Volume Fraction: 30% |
|
Sand |
Density: 2,650kg/m3, Particle Diameter: 0.2mm |
|
Water |
Density: 1,000kg/m3, Dynamic Viscosity:0.001004Pa¬ЈsвАГ |
Fig. 1

Fig. 2
Comparison of the Simulation Result about Volume Fraction
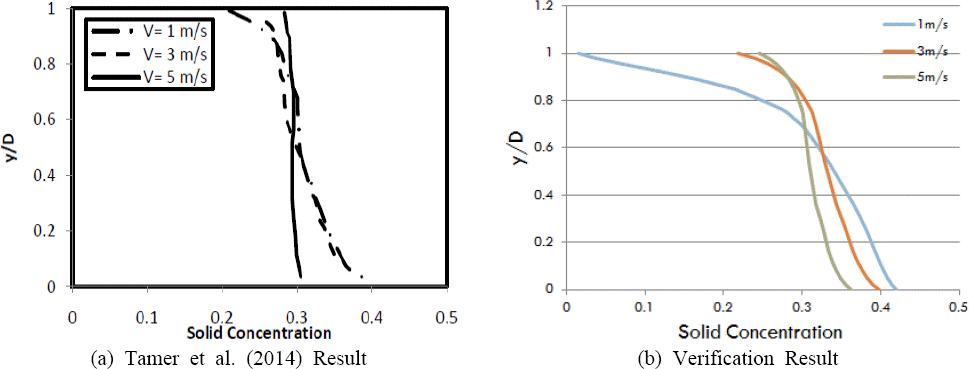
Fig. 3
Comparison of the Simulation Result about Velocity Profile
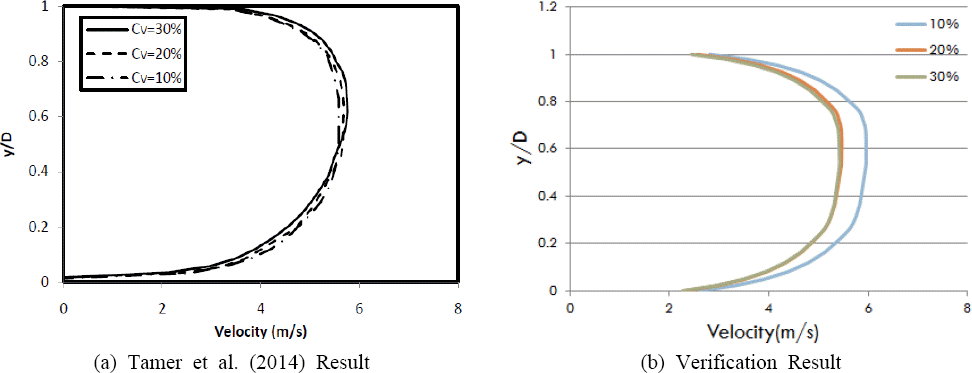
Table 5
Sedimentation Result of Simulation Inside the Pipe(kg)
|
Condition |
SandDia-meter (mm) |
Volume Fraction 10% |
Volume Fraction 30% |
Volume Fraction 50% |
|
Velocity (m/s) |
|
0 ° |
1 ° |
3 ° |
5 ° |
0 ° |
1 ° |
3 ° |
5 ° |
0 ° |
1 ° |
3 ° |
5 ° |
|
1.0 |
1.0 |
2,074 |
1,885 |
1,681 |
1,565 |
4,756 |
4,253 |
3,770 |
3,065 |
6,789 |
6,538 |
5,776 |
5,453 |
|
3.0 |
2,407 |
2,161 |
1,915 |
1,647 |
5,105 |
4,651 |
3,974 |
3,445 |
6,829 |
6,635 |
6,014 |
5,510 |
|
5.0 |
2,605 |
2,582 |
2,222 |
2,051 |
6,423 |
4,967 |
4,145 |
3,377 |
6,935 |
6,726 |
6,048 |
5,766 |
|
2.0 |
1.0 |
1,886 |
1,762 |
1,762 |
1,709 |
4,154 |
3,474 |
3,474 |
3,192 |
6,811 |
6,429 |
6,429 |
6,182 |
|
3.0 |
2,242 |
1,885 |
1,885 |
1,765 |
4,892 |
4,221 |
4,221 |
3,441 |
7,364 |
6,658 |
6,658 |
6,449 |
|
5.0 |
2,697 |
2,420 |
2,420 |
2,151 |
5,960 |
5,134 |
5,134 |
4,179 |
7,412 |
6,926 |
6,926 |
6,603 |
|
3.0 |
1.0 |
1,745 |
1,640 |
1,640 |
1,606 |
4,217 |
4,032 |
4,032 |
3,768 |
6,653 |
5,965 |
5,965 |
5,836 |
|
3.0 |
1,767 |
1,640 |
1,640 |
1,581 |
4,555 |
4,112 |
4,112 |
3,914 |
7,267 |
6,018 |
6,018 |
5,882 |
|
5.0 |
1,805 |
1,779 |
1,779 |
1,725 |
4,924 |
4,336 |
4,336 |
4,208 |
7,435 |
6,107 |
6,107 |
6,082 |
3.2 мЬ†мґЬкµђ нЗім†БлЯЙ мЬ†мґЬнКємД±
нШЉмЮЕлРЬ мГБнГЬл°Ь мЬ†мЮЕлРЬ мЬ†м≤імЩА нЖ†мВђлЯЙмЭА кіАлВілґАл•Љ нЭШлЯђк∞Ал©імДЬ лґДнПђнШХнГЬк∞А мІАмЖНм†БмЬЉл°Ь л≥АнХШл©∞, мЛЬк∞Д к≤љк≥ЉмЧР лФ∞лЭЉ мЭЉм†ХлЯЙ нЗім†БмЭі л∞ЬмГЭнХШк≤М лРЬлЛ§. мЭіл†Зк≤М нЗім†БлРЬ нЖ†мВђлКФ кіАк±∞ нКєм†Х мЬДмєШмЧРмДЬ м†Рм∞® м¶Эк∞АлРШл©імДЬ нХілЛєкµђк∞ДмЧРмДЬмЭШ кµ≠лґАм†БмЭЄ мЬ†мЖНмЭШ мГБмКємЭД міИлЮШнХЬлЛ§. нХШмІАлІМ мЭілЯђнХЬ нШДмГБмЭі кіАк±∞ лВілґАмЧРмДЬ л∞Шл≥µм†БмЭЄ нШХнГЬл•Љ мЭіл£®л©∞ к≤∞кµ≠ мЬ†мґЬкµђ л∞©нЦ•мЬЉл°Ь мЭілПЩнХік∞Ал©∞ л∞∞мґЬнХШк≤М лРЬлЛ§. к≤∞кµ≠ мЭілЯђнХЬ нМ®нДімЭД л∞Шл≥µнХШл©імДЬ нЗім†БлЯЙмЭі мВ∞мґЬлРШлКФлН∞ мЭілХМ мЬ†мЖНмЭілВШ лЖНлПДмЧР лФ∞лЭЉ л∞∞мґЬлРШлКФ нМ®нДімЭД нММмХЕнХ† нХДмЪФк∞А мЮИлЛ§.
л≥Є мЧ∞кµђмЧРмДЬ мІДнЦЙнХЬ 108к∞ЬмЭШ лґДмДЭ к≤љмЪ∞мЧР лМАнХі нХімДЭнХЬ к≤∞к≥Љл•Љ л∞ФнГХмЬЉл°Ь кіАк±∞ лВілґАмЧРмДЬмЭШ мЬ†м≤імЩА нЖ†мВђмЭШ нЭРл¶Д лґДнПђмЧР лМАнХЬ к≤∞к≥Љл•Љ кіАм∞∞нХШмШАмЬЉл©∞, кЈЄ к≤∞к≥Љ мЬ†мґЬкµђмЧРмДЬ л∞∞мґЬлРШлКФ нЖ†мВђнЗім†БлЯЙмЭШ нМ®нДімЭА мДЄ к∞АмІА нШХнГЬл°Ь лВШнГАлВімЧИлЛ§.
Figs. 4вИЉ
6мЭА мЬ†мЮЕмЬ†мЖН 1m/s, нЖ†мВђ мІБк≤љ 5.0mmмЭШ 0¬∞ м°∞к±і кіАк±∞мЧРмДЬ мЬ†м≤імЩА нЖ†мВђмЭШ лЖНлПДл•Љ л≥АнЩФмЛЬмЉЬк∞Ал©∞ кіАк±∞мЭШ мЬ†мґЬкµђмЧРмДЬ лґДмДЭлРЬ к≤∞к≥Љл•Љ лВШнГАлВЄлЛ§.
Fig. 4 к≤∞к≥Љл•Љ мВінОіл≥іл©і мЬ†мґЬкµђмЧРмДЬ лє†м†ЄлВШк∞АлКФ нЖ†мВђлЯЙмЭі мЭЉм†ХнХЬ м£ЉкЄ∞мЩА к∞Дк≤©мЭД нШХмД±нХШк≥† мЮИлЛ§. мЭілКФ кіАк±∞ лВілґАмЧРмДЬлПД нЗім†Бк≥†л•Љ нШХмД±нХШлКФ лЖТмЭімЩА мЭіл•Љ лВШнГАлВілКФ кµђк∞ДмЭШ нП≠мЭі мЭЉм†ХнХШк≤М нШХмД±лРШл©∞ мЬ†мґЬкµђ л∞©нЦ•мЬЉл°Ь мЭілПЩнХ®мЭД мХМ мИШ мЮИлЛ§. мЭілЯђнХЬ нМ®нДімЭА кіАлВі нЖ†мВђмЭШ нЗім†БлЯЙмЭі мЭЉм†ХнХЬ м£ЉкЄ∞л•Љ к∞Цк≥† кіАк±∞ мЬ†мґЬкµђ л∞©нЦ•мЬЉл°Ь нЦ•нХі лє†м†ЄлВШк∞РмЭД мЭШлѓЄнХШл©∞, мЬ†мЮЕ мЬ†мЖНмЧР лєДнХі мЮЕмЮРмЭШ нБђкЄ∞ л∞П лЖНлПДк∞А лВЃмХД м†Дл∞Шм†БмЬЉл°Ь мЫРнЩЬнЮИ л∞∞мґЬлРШлКФ нШХнГЬл•Љ лЭДк≥† мЮИлЛ§.
Figs. 5мЩА
6мЭШ к≤љмЪ∞мЧРлКФ мХЮмДЬ лПЩмЭЉнХЬ нМ®нДімЧР лєДнХі м†Рм∞® л∞∞мґЬлРШлКФ к∞Дк≤©мЭі мЮ¶мХДлУЬлКФ к≤ГмЭД л≥Љ мИШ мЮИлЛ§. мЭілКФ кіАк±∞ лВілґАмЧРмДЬ м†Рм∞® нЗім†БлРЬ нЖ†мВђк∞А к≤љнЩФлРЬ нШДмГБмЬЉл°Ь кіАк±∞ л∞ФлЛ•мЧР м¶Эм∞©лРШмЦі м†Бм†Х нЖµмИШлК•мЭД нШХмД±нХШмІА л™їнХ®мЭД мЭШлѓЄнХЬлЛ§. міИл∞ШлґА мЬ†мґЬмЭД м†ЬмЩЄнХШк≥† мЬ†мЮЕлРШлКФ мЦСк≥Љ лПЩмЭЉнХЬ мЬ†мґЬнШДмГБмЭШ к≤љмЪ∞ мЬ†мЖНмЧР мЮЕмЮРмЭШ нБђкЄ∞к∞А нБђк≥† лЖНлПДк∞А нБ∞ к≤љмЪ∞мЧР кіАм∞∞лРШмЧИлЛ§. л≥Є мЧ∞кµђмЧРмДЬ лґДмДЭнХЬ м†Дм≤і 108к∞ЬмЭШ лґДмДЭ к≤∞к≥Љ л™®лСР мЬД мДЄ к∞АмІА нКємД±мЬЉл°Ь лґДл•ШлРШмЧИлЛ§. кЈЄлЯђлВШ лґДмДЭ м°∞к±і л≥Дл°Ь мЬ†мґЬнКємД±мЭД нЖµнХі лВШнГАлВЬ нЗім†БмЭШ нМ®нДімЭА м†ХмД±м†БмЭЄ к≤љнЦ•мД±мЧР лМАнХЬ мЭЉм†Х мґФм†ХмЭА к∞АлК•нХШмІАлІМ лВілґАмЭШ мЬ†мЖН л∞П мХХ놕 нКємД±мЭД нЖµнХі л™ЕнЩХнХЬ лґДмДЭмЭі нХДмЪФнХШлЛ§к≥† нМРлЛ®лРЬлЛ§.
Fig. 4
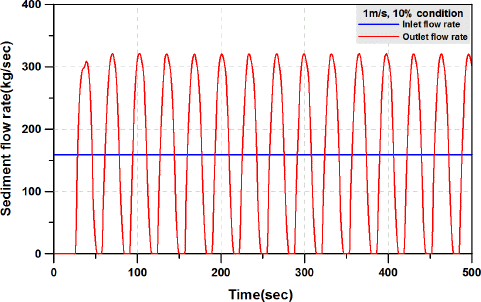
Fig. 5

Fig. 6
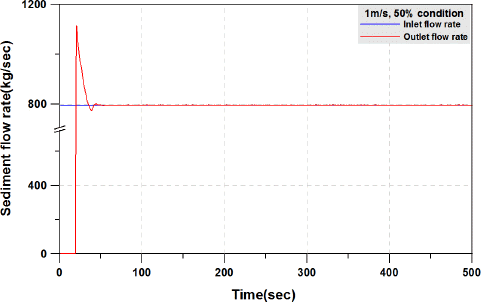
Fig. 7
Sedimentation Predict Equation for Low Volume Fraction

Fig. 8
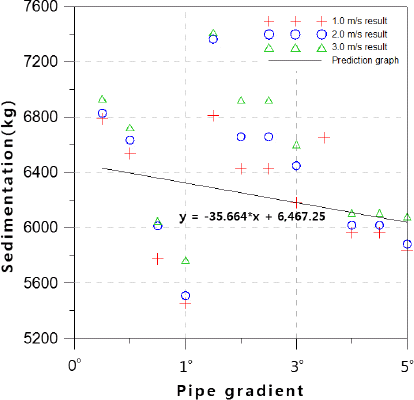
Sedimentation Predict Equation for Mid Volume Fraction
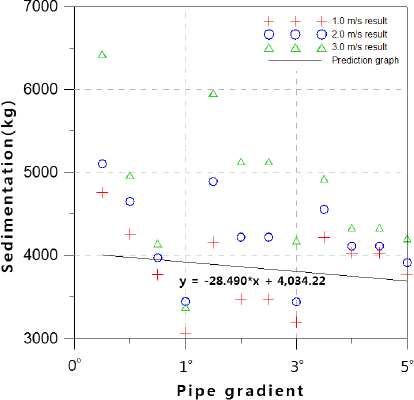
Fig. 9
Sedimentation Predict Equation for High Volume Fraction
3.3 нЗім†БнЖ†мВђлЯЙ к≤∞к≥Љ
л≥Є мЧ∞кµђмЧРмДЬлКФ Mass Balance кіАк≥Дл•Љ мЭімЪ©нХШмЧђ мЬ†м≤імЩА нЖ†мВђлЯЙмЭШ мЬ†мЮЕ-мЬ†мґЬ кіАк≥Дл•Љ л∞ФнГХмЬЉл°Ь кіАлВі нЖ†мВђнЗім†БлЯЙмЭД мВ∞м†ХнХШмШАлЛ§. мВ∞м†Х к≤∞к≥Љ кіАк±∞мЭШ к≤љмВђлПД м¶Эк∞АмЧР лФ∞л•Є нЗім†БлЯЙмЭШ л≥АнЩФлКФ нБђк≤М л≥АнЩФнХШлКФ к≤ГмЬЉл°Ь лВШнГАлВђлЛ§. лНФлґИмЦі мЮЕмЮРмЭШ нБђкЄ∞мЩА мЬ†м≤ілВі нЖ†мВђмЭШ лЖНлПДмЭШ кіАк≥ДмЧР лФ∞лЭЉ нЗім†БмЭШ л≥АнЩФлЯЙмЭі нБђк≤М лВШнГАлВШлКФ к≤ГмЬЉл°Ь лґДмДЭлРШмЧИлЛ§. нЖ†мВђк∞А 10%мЭШ лЖНлПДл°Ь мЬ†мЮЕлРЬ к≤љмЪ∞ кіАк±∞лВі л∞ЬмГЭ нЗім†БлЯЙмЭі кіАк±∞ м≤ім†БлМАлєД мХљ 25%м†ХлПДл°Ь мВ∞м†ХлРШмЧИлЛ§. 30% лЖНлПДмЭШ к≤љмЪ∞лКФ нПЙкЈ† 57%л°Ь лВШнГАлВђмЬЉл©∞, 50%мЭШ к≤љмЪ∞ мХљ 86%л°Ь кіАк±∞мЭШ нПРмГЙмЧР к∞АкєЭк≤М лВШнГАлВђлЛ§. лЖНлПД м¶Эк∞АмЧР лФ∞лЭЉ нЗім†БлЯЙмЭі лСРлУЬлЯђмІАк≤М м¶Эк∞АнХШлКФ к≤љнЦ•мЭД лВШнГАлВімЧИмЬЉлВШ л≥Є мЧ∞кµђмЧРмДЬ м†БмЪ©нХЬ 1.0вИЉ3.0mm мІБк≤љмЭШ нЖ†мВђ мЮЕмЮРмЧР лФ∞лЭЉмДЬлКФ лЪЬл†ЈнХЬ л≥АнЩФл•Љ л≥імЭімІА мХКлКФ к≤ГмЬЉл°Ь лґДмДЭлРШмЧИлЛ§. кіАк±∞мЭШ кЄ∞мЪЄкЄ∞мЧР лФ∞л•Є к∞РмЖМ к≤љнЦ•мД±мЭД мВінОіл≥іл©і мµЬміИ кіАк±∞мЭШ к≤љмВђк∞А мЧЖлКФ мГБнГЬмЭШ нЗім†БлЯЙмЭД кЄ∞м§АмЬЉл°Ь 1¬∞ кЄ∞мЪЄкЄ∞мЧР лФ∞лЭЉ мХљ 10%мЭШ к∞РмЖМл•Љ л≥імШАмЬЉл©∞ 3¬∞мЩА 5¬∞л°Ь кЄ∞мЪЄкЄ∞к∞А м¶Эк∞АнХ†мИШл°Э мХљ 14%, 20%мЭШ к∞РмЖМ к≤љнЦ•мД±мЭД нЩХмЭЄнХШмШАлЛ§.
мЭілЯђнХЬ к≤∞к≥ЉлКФ к≤љмВђлПДк∞А мЮСмЭА кіАк±∞мЧР лєДнХі к≤љмВђк∞А мї§мІИмИШл°Э л∞ШмЭСнХ† мИШ мЮИлКФ нЖµмИШ лЛ®л©ім†БмЭі лДУмЦімІАк≤М лРЬлЛ§. лЛ§мЛЬлІРнХі нЖ†мВђлЯЙмЭД мЬ†мґЬкµђл°Ь мЭімЖ°мЛЬнВ§кЄ∞ мЬДнХЬ мЬ†м≤імЩАмЭШ л∞ШмЭСмЭі к≤љмВђлПДк∞А мЮСмЭА лЛ®л©імЭД кµђмД±нХШлКФ кіАк±∞мЧР лєДнХімДЬ нБ∞ к≤љмВђлПДл•Љ к∞АмІД лЛ®л©імЭД нПђнХ®нХШлКФ кіАк±∞мЧРмДЬ л∞ШмЭСмЭі нБђк≤М мЭЉмЦілВШ нЗім†БмЭШ к≤љнЦ•мЭі к∞РмЖМнХЬлЛ§к≥† нМРлЛ®нХ† мИШ мЮИлЛ§. мЭілЯђнХЬ нЗім†БлЯЙмЭШ к∞РмЖМмґФмДЄл•Љ л≥Љ лХМ, мЛ§м†Ь кіАк±∞ мД§к≥ДмЛЬ мІАнСЬмЧРмДЬ л∞ЬмГЭк∞АлК•нХЬ нЖ†мВђлЯЙмЭД нММмХЕнХШк≥† кіАк±∞мЛЬмК§нЕЬ лВілґАл°Ь мЬ†мЮЕлРШлКФ нШХнГЬл•Љ мШИмЄ°нХЬлЛ§л©і л∞ЬмГЭк∞АлК•нХЬ нЗім†БмЭШ л≤ФмЬД мґФм†ХмЭі к∞АлК•нХШлЛ§к≥† нМРлЛ®лРЬлЛ§. мЭіл•Љ л∞ФнГХмЬЉл°Ь кіАк±∞мЛЬмК§нЕЬ лВілґА мИШл¶ђкµђм°∞лђЉмЧР нЗім†БлЯЙмЭД к≥†л†§нХШмЧђ мД§к≥ДмЛЬ кіАк≤љк≥Љ к≤љмВђлПДмЭШ к≤АнЖ†к∞А нХДмЪФнХШлЛ§к≥† нМРлЛ®лРЬлЛ§.
к≤∞к≥Љм†БмЬЉл°Ь кіАк±∞ к≤љмВђк∞А м¶Эк∞АмЧР лФ∞л•Є нЖ†мВђ мЮЕмЮРлУ§ к∞ДмЭШ м¶Эм∞©мЭШ к≤љнЦ•мД±мЭі к∞РмЖМлРШмЦі нЗім†БлЯЙмЭі м§ДмЦілУЬлКФ к≤ГмЭД нЩХмЭЄнХ† мИШ мЮИмЧИмЬЉл©∞, мЭілКФ кіАк±∞ лВілґАмШБмЧ≠мЧРмДЬ м°імЮђнХШлКФ мЬ†мґЬлЯЙмЭШ нЭРл¶Дкµђк∞ДмЭі м¶Эк∞Ал°Ь мЭімЦімІДлЛ§к≥† нМРлЛ®лРЬлЛ§. мЭілЯђнХЬ нХімДЭк≤∞к≥ЉлУ§мЭД л∞ФнГХмЬЉл°Ь кіАк±∞ лВілґАл°Ь мЬ†мЮЕлРШлКФ мЬ†мВђлЯЙмЭШ лЖНлПДл•Љ кЄ∞м§АмЬЉл°Ь л∞ЬмГЭ к∞АлК•нХЬ нЗім†БлЯЙмЭШ мґФм†ХмЛЭмЭД Eqs. 6вИЉ8мЧР лЖНлПДл≥ДлПД м†ЬмХИнХШмШАмЬЉл©∞, нЦ•нЫД кіАк±∞ мЬ†мІАкіАл¶ђ л∞П нЪ®мЬ®м†БмЭЄ кіАк±∞мД§к≥Дл•Љ мЬДнХЬ кЄ∞міИмЮРл£Мл°Ь нЩЬмЪ©нХШк≥†мЮР нХЬлЛ§.
4. к≤∞л°† л∞П нЦ•нЫД мЧ∞кµђл∞©нЦ•
л≥Є мЧ∞кµђмЧРмДЬлКФ лПДмЛђмІА мЪ∞мИШкіАк±∞ лВілґАл°Ь мЬ†мЮЕлРШлКФ нЖ†мВђмЧР лМАнХЬ мЭімЖ°вЛЕмє®м†Д нХімДЭмЭД мЛ§мЛЬнХШмШАлЛ§. CFD Fluent нХімДЭл™®нШХмЭД мЭімЪ©нХШмЧђ нЗім†БлЯЙ мВ∞м†ХмЭД мЬДнХЬ м†Хл∞АнХімДЭ л∞©л≤ХмЭД м†ЬмЛЬнХШк≥†, мЭімЧР лМАнХЬ лґДмДЭмЭД мИШнЦЙнХШмШАлЛ§. кіАк±∞л°Ь мЬ†мЮЕлРШлКФ мЬ†м≤імЩА нЖ†мВђмЮЕмЮР, лЖНлПД л∞П мЬ†мЖНмЭШ м°∞к±імЭД л∞ФнГХмЬЉл°Ь к≤љмВђлПДл≥Д нЗім†Бл∞ЬмГЭлЯЙмЭД мВ∞м†ХнХШмШАмЬЉл©∞ лЖНлПДл≥Д мШИмГБнЗім†БлЯЙ мґФм†ХмЛЭмЭД м†ЬмХИнХШмШАлЛ§.
мЪ∞мИШкіАк±∞ лВілґАл°Ь мЬ†мЮЕлРШлКФ мЬ†м≤імЧР нЖ†мВђлЯЙмЭД к≥†л†§нХ®мЬЉл°ЬмН® м†Хл∞АнХЬ кіАк±∞ лВілґА нЭРл¶Д лґДмДЭмЧР лМАнХЬ к≥†л†§ мЧЖмЭі м݊땆м†БмЬЉл°Ь м†БмЪ©нХШк≥† мЮИлКФ мЬ†мЖНмЧР кіАнХЬ мД§к≥ДкЄ∞м§АмЭА мЪ∞мИШкіАк±∞мЧР мЮИмЦі мЫРнЩЬнХЬ нЖµмИШлК•мЧР мІАмЮ•мЭД м§Д лњРлІМ мХДлЛИлЭЉ нЩНмИШмЛЬ л∞ЬмГЭлР† мИШ мЮИлКФ мЮРмЧ∞мЮђнХі лУ±к≥Љ к∞ЩмЭА нБ∞ мШБнЦ•мЭД лБЉмє† мИШ мЮИлЛ§. мЭіл°†м†БмЭЄ м†СкЈЉк≥Љ лНФлґИмЦі мДЄл∞АнХЬ лґДмДЭмЭД л∞ФнГХмЬЉл°Ь л≥ілЛ§ нХ©л¶ђм†БмЭЄ мЪ∞мИШкіАк±∞ нЖµмИШлК• к≤АнЖ† л∞П мД§к≥ДмХИ лПДмґЬмЭі л≥Є мЧ∞кµђмЭШ кґБкЈєм†БмЭЄ л™©нСЬмЭілЛ§.
нЦ•нЫД мЬ†мЮЕнЖ†мВђлЯЙк≥Љ мЪ∞мИШкіАк±∞ лВі мИШл¶ђнХЩм†Б мЭЄмЮРл•Љ л∞ШмШБнХШмЧђ нЖ†мВђмЭШ мЭімЖ°вЛЕмє®м†Д нХімДЭ к≤∞к≥Љл•Љ л∞ФнГХмЬЉл°Ь лЛ§мЦСнХЬ л™®нШХ л≥АмИШмЭШ м†БмЪ©мЧР лФ∞л•Є л∞ЬмГЭ нХЬк≥Дм†РмЭД м†Хл¶ђк∞А нХДмЪФнХШлЛ§. мЭіл•Љ л∞ФнГХмЬЉл°Ь мЛ§м†Ь кіАк±∞ лВілґАмЧРмДЬ л∞ЬмГЭнХШлКФ нЗім†Б нКємД±мЧР лМАнХЬ л™®мЭШнШДмГБмЭД л∞ШмШБнХЬ мХМк≥†л¶ђм¶ШмЭШ кµђмґХмЭі нХДмЪФнХШлЛ§. л≥Є лЕЉлђЄмЧРмДЬ мІДнЦЙнХЬ mass balanceл•Љ к≥†л†§нХЬ кіАлВі нЗім†БлЯЙ мШИмЄ°мЭД нЖ†лМАл°Ь л≥µмЮ°нХЬ лПДмЛђмІА мЪ∞мИШкіАк±∞ мД§к≥Д кµђмД± лУ±мЧР мЭШнХЬ мИШл¶ђнХЩм†Б нЗім†Бл∞ЬмГЭ мШИмЄ°мЭШ к≥†л†§к∞А к∞АлК•нХШлЛ§. мµЬмҐЕм†БмЬЉл°Ь лПДмЛђмІА мЪ∞мИШкіАк±∞мЭШ мД§к≥ДмЛЬ м±ДнГЭнХШк≥† мЮИлКФ кіАк±∞ лІ§к∞Ьл≥АмИШ м†БмЪ©к≥Љ кіАлВіл•Љ нЭРл•ілКФ мЬ†м≤імЩА нЖ†мВђ мЮЕмЮРмЭШ нХімДЭкЄ∞мИ†мЭШ м†ЬмЛЬл•Љ нЖµнХі лПДмЛђмІА мЬ†мґЬл™®нШХмЭД к∞ЬмД†нХШлКФ к≤ГмЭі л≥Є мЧ∞кµђмЭШ л™©нСЬмЭіл©∞, нЖ†мВђм†Ал•Шм°∞лВШ лєЧлђЉнОМнФДмЮ• лУ±мЭШ лВіл∞∞мИШ мЛЬмК§нЕЬмЭШ нЪ®к≥Љм†БмЭЄ мД§к≥Д л∞П мЪімШБмЧРлПД лПДмЫАмЭі лР† к≤ГмЬЉл°Ь кЄ∞лМАлРЬлЛ§. л≥Є мЧ∞кµђмЧРмДЬ м†ЬмХИнХЬ мЪ∞мИШкіАк±∞лВі нЖ†мВђнЗім†БлЯЙ мВ∞м†Х кЄ∞л≤ХмЭА мЪ∞мИШкіАк±∞ мЛЬмК§нЕЬ мД§к≥ДмЛЬ кЄ∞л≥Єм†БмЭЄ мЮРл£МмЩА мЭСмЪ© кЄ∞мИ†мЭД м†Ьк≥µнХ®мЬЉл°ЬмН® лПДмЛЬ нЩНмИШ л∞©мЦімЧР лМАнХЬ кЄ∞міИмЮРл£М мИШмІС л∞П мЛ§мЪ©мД±л©імЧРмДЬ к≤љм†Ьм†Б нЪ®к≥Љл•Љ кЄ∞лМАнХ† мИШ мЮИлЛ§.
к∞РмВђмЭШ кЄА
л≥Є мЧ∞кµђлКФ кµ≠лѓЉмХИм†Дм≤Ш мЮРмЧ∞мЮђнХім†Ак∞РкЄ∞мИ†к∞Ьл∞ЬмВђмЧЕлЛ®(мЮРмЧ∞нФЉнХімШИмЄ°л∞Пм†Ак∞РмЧ∞кµђк∞Ьл∞ЬмВђмЧЕ)мЭШ мІАмЫРмЬЉл°Ь мИШнЦЙнХЬ вАШкЄ∞нЫДл≥АнЩФ м†БмЭСмЭД мЬДнХЬ мЧ∞мХИлПДмЛЬмІАмЧ≠л≥Д л≥µнХ©мЫРмЭЄмЭШ нЩНмИШ мЈ®мХљмД± нПЙк∞АкЄ∞мИ† к∞Ьл∞Ь л∞П лМАмЭС л∞©мХИ мЧ∞кµђвАЩ [MPSS-мЮРмЧ∞-2015-77]к≥Љм†ЬмЭШ мД±к≥ЉмЮЕлЛИлЛ§.
References
Ashley, R. M, Bertrand-Krajewski, J. L, Hvitved-Jacobsen, T, and Verbanck, M (
Solids in Sewers: Characteristics. 2004). IWA Publishing, No. 14.

Becouze-Lareure, , Dembele, A, Coquery, M, Cren-Olive, C, Barillon, B, and Bertrand-Krajewski, J-L (Source Characterisation and Loads of Metals and Pesticides in Urban Wet Weather Discharges.
Urban Water Journal, 2016) Vol. 13, No. 6, pp. 600-617. 10.1080/1573062X.2015.1011670.

Bertrand-Krajewski, J. L, Barraud, S, Kouyi, G. L, Torres, A, and Lepot, M (On-line Monitoring of Particulate Pollutant Loads in Urban Sewer Systems: Stakes, Methods, Example of Application.
La Houille Blanche, 2008) Vol. 4, pp. 49-57. 10.1051/lhb:2008039.

Chebbo, G, and Bachoc, A (Characterization of Suspended Solids in Urban Wet Weather Discharges.
Water Science and Technology, 1992) Vol. 25, No. 8, pp. 171-179.

Choi, S. H, and Lee, S. O (The Numerical Simulation Considering Air Pressure and the Influence Factor Analysis of Geyser in a Stormwater Tunnel with Large Diameter.
Journal of Korean Society of Hazard Mitigation, 2016) Vol. 16, No. 2, pp. 133-139. 10.9798/KOSHAM.2016.16.2.133.

Kim, S. Y, Kim, J. S, and Yoon, S. E (Analysis of Discharge Capacity for Intake Structure at Deep Underground Storm Water Tunnel Using Fluent Model.
Journal of Korean Society of Hazard Mitigation, 2014) Vol. 14, No. 2, pp. 255-265. 10.9798/KOSHAM.2014.14.2.255.

Lipeme, Kouyi G (Experimentations et Modelisations Tridimensionnelles DelвАЩhydrodynamique et de la Separation Particulaire dans les Deversoirs DвАЩorage.
Ph.D. thesis. 2004). University of Pasteur, France.

Ministry of Environment (
Facility Standard For Drainage System. 2011.

Stovin, V. R (The Prediction of Sediment Deposition in Storage Chambers Based on Laboratory Observations and Numerical Simulation.
Ph.D. thesis. 1996). UK: University of Sheffield.

Tamer, N, Imam, E. S, and Kamal, E.N (Sand-Water Slully Flow Modelling in a Horizontal Pipeline by Computational Fluid Dynamic Technique.
International Water Technology Journal, 2014) Vol. 4, No. 1, pp. 1-17.

Versteeg, H. K, and Malalasekera, W (
An Introduction to Computational Fluid Dynamics(Second Edition). 2007). Pearson Education Limited.


















