1. мДЬ л°†
2. мЭіл°†м†Б л∞∞к≤љ
2.1 нИђмЮРмЪ∞мД†мИЬмЬД к≤∞м†ХмЭД мЬДнХЬ нЩНмИШмЈ®мХљмД± мВ∞м†Х л∞©л≤Х
2.1.1 нЩНмИШнФЉнХімЮ†мЮђлК• (Potential Flood Damage, PFD)
2.1.2 нЩНмИШмЬДнЧШлПД мІАнСЬ(Flood Risk Indices)
2.2 нЩНмИШмЈ®мХљмД± нХ≠л™©л≥Д к∞Ам§СмєШ к≤∞м†Х л∞©л≤Х
2.2.1 AHP(Analytic Hierachy Process) к∞Ам§СмєШ л∞©л≤Х
2.2.2 мЧФнКЄл°ЬнФЉ(Entropy) к∞Ам§СмєШ л∞©л≤Х
3. нЩНмИШмЈ®мХљмД± мВ∞м†Х л∞П мєШмИШ нИђмЮРмЪ∞мД†мИЬмЬД к≤∞м†Х
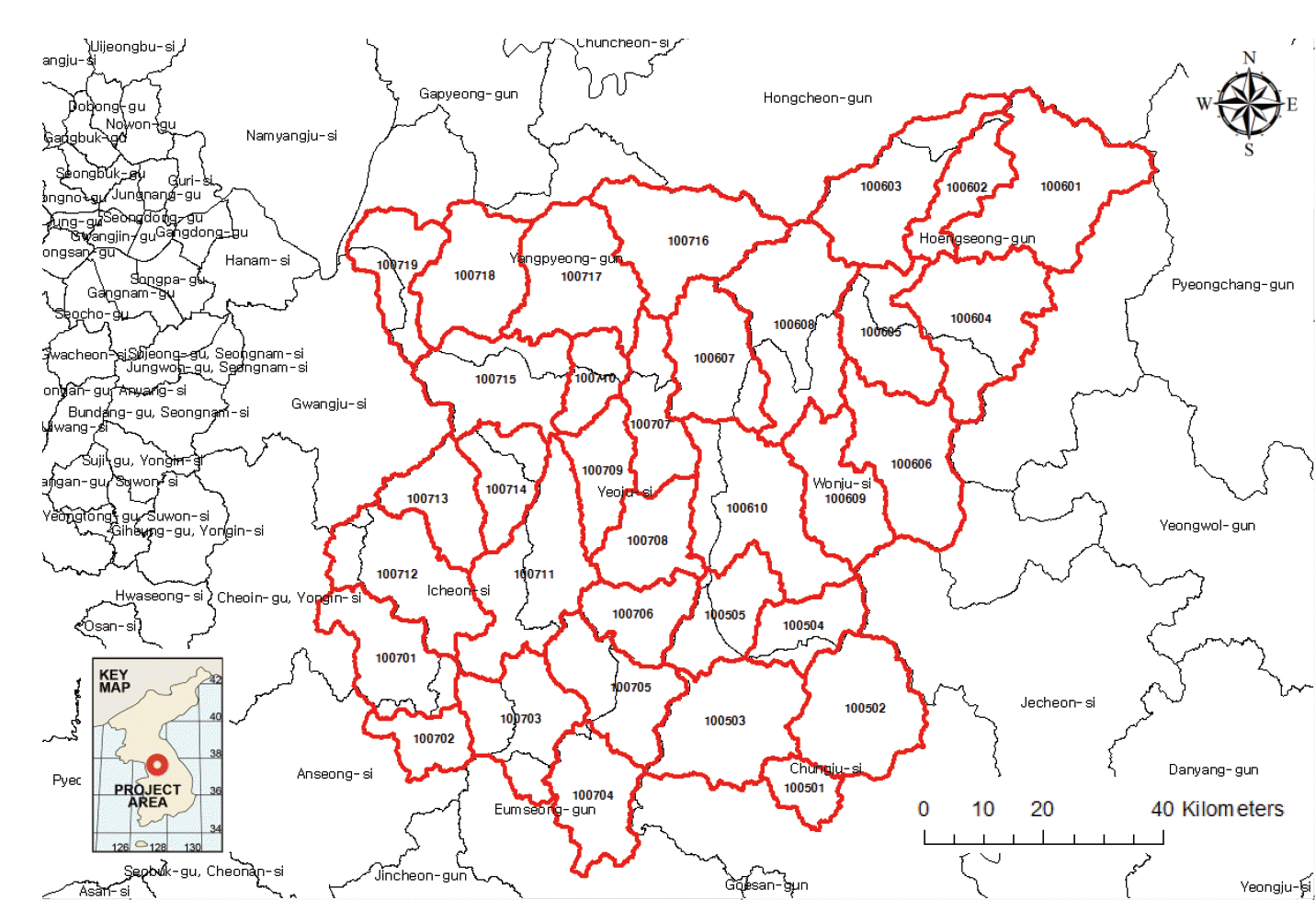
3.1 лМАмГБ мІАмЧ≠ мД†м†Х
3.2 нЩНмИШмЈ®мХљмД± мВ∞м†Х
3.2.1 нЩНмИШмЈ®мХљмД± мВ∞м†ХмЭД мЬДнХЬ к∞Ам§СмєШ к≤∞м†Х л∞©л≤Х
вЦ° Weight 1: кЄ∞м°і к∞Ам§СмєШ л∞©л≤Х (мИШмЮРмЫРмЮ•кЄ∞мҐЕнХ©к≥ДнЪН)
вЦ° Weight 2: AHPмЧР мЭШнХЬ к∞Ам§СмєШ л∞©л≤Х
вЦ° Weight 3: мЧФнКЄл°ЬнФЉмЧР мЭШнХЬ к∞Ам§СмєШ л∞©л≤Х
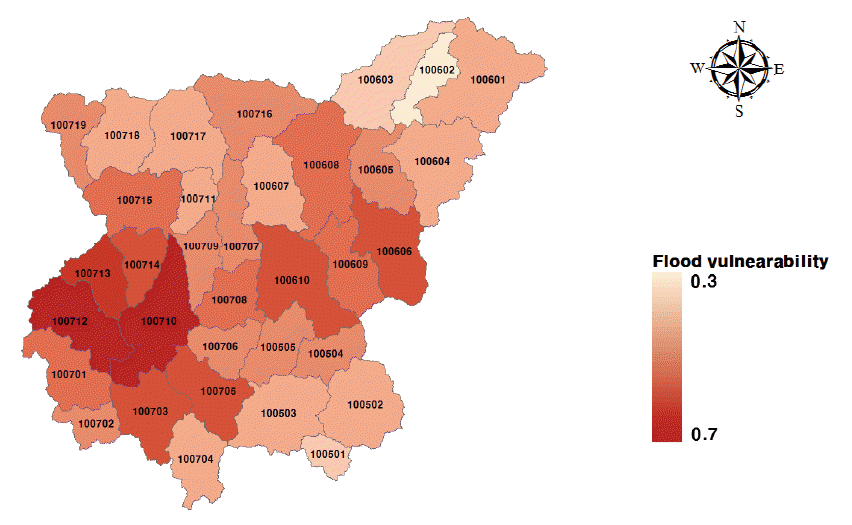
3.2.2 к∞Ам§СмєШл•Љ к≥†л†§нХЬ нЩНмИШмЈ®мХљмД± мВ∞м†Х
(1) к∞Б нЩНмИШмЈ®мХљмД±мЭШ нХ≠л™©л≥Д(нШДмЮђ кЄ∞м§А) мЮРл£Мл•Љ мИШмІСнХЬлЛ§.
(2) мИШмІСлРЬ мЮРл£Мл•Љ л∞ФнГХмЬЉл°Ь м†ХкЈЬ лґДнПђл•Љ нЖµнХЬ м݊놮мЭШ м†ХкЈЬнЩФ к≥Љм†ХмЭД к±∞мєЬлЛ§.
(3) мХЮмДЬ м†ЬмЛЬнХЬ к∞Ам§СмєШл≥Дл°Ь нЩНмИШмЈ®мХљмД± нПЙк∞А мВ∞м†ХмЛЭмЭД м†БмЪ©нХЬлЛ§.
(4) мµЬмҐЕм†БмЭЄ к∞Ам§СмєШл≥Д к≤∞к≥Љк∞ТмЭД лПДмґЬнХЬлЛ§.
4. мєШмИШ нИђмЮРмЪ∞мД†мИЬмЬД к≤∞м†Х л∞П мВђмЧЕмЛЬлВШл¶ђмШ§мЧР лФ∞л•Є кЄ∞лМАнЪ®к≥Љ
4.1 мєШмИШ нИђмЮРмЪ∞мД†мИЬмЬД к≤∞м†Х
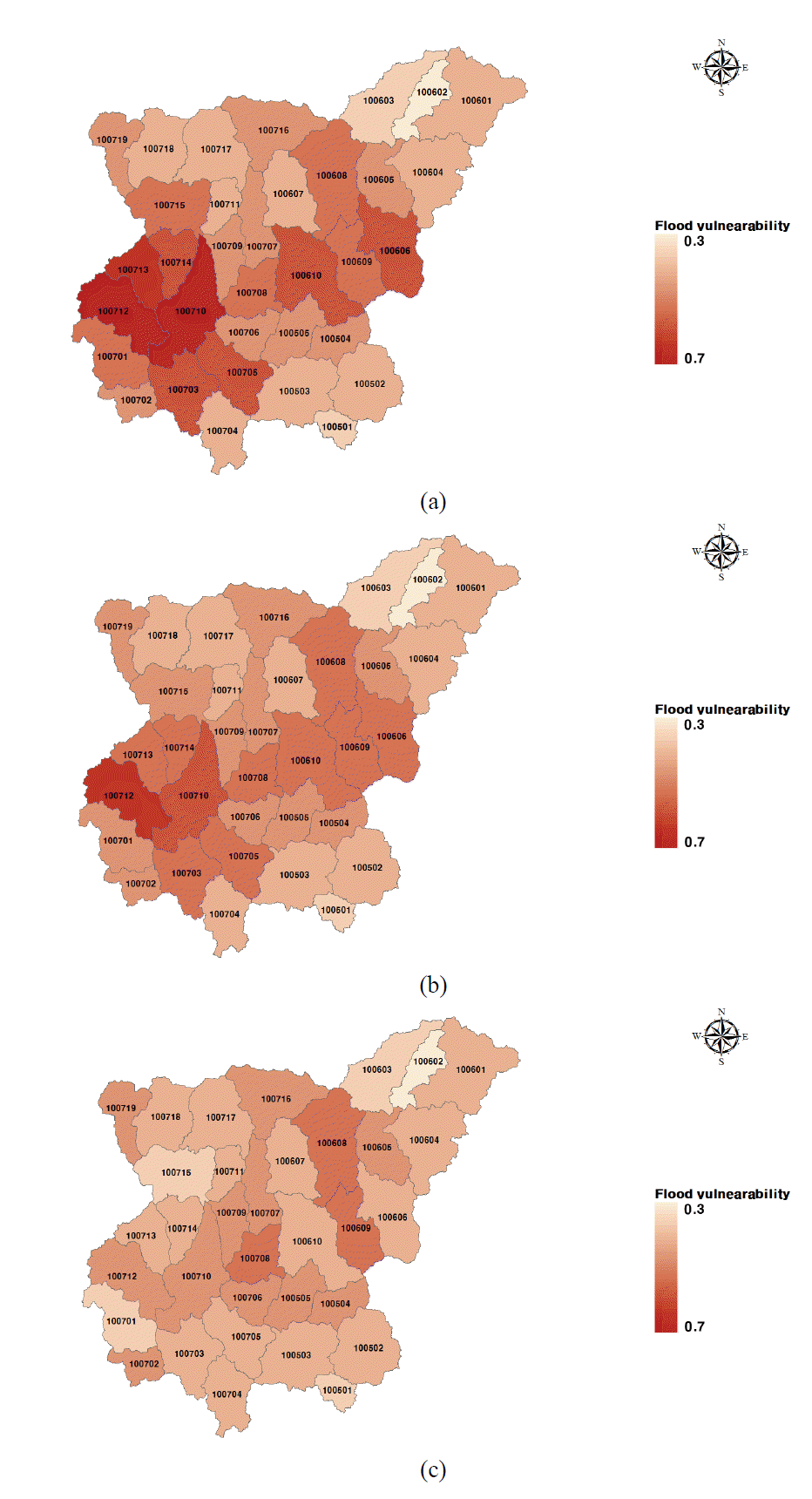
4.2 мєШмИШмВђмЧЕ мЛЬлВШл¶ђмШ§мЧР лФ∞л•Є нИђмЮРмЪ∞мД†мИЬмЬД кЄ∞лМАнЪ®к≥Љ
5. к≤∞ л°†
(1) нШДмЮђ мєШмИШ нИђмЮР мЪ∞мД†мИЬмЬДлКФ м§СкґМмЧ≠ 1006 л∞П 1007 мЭінХШмЭШ нСЬм§АмЬ†мЧ≠мЭі мЪ∞мД†мИЬмЬДк∞А лєДкµРм†Б лЖТк≤М мВ∞м†ХлРШмЧИлЛ§. нКєнЮИ, 100701~100715мЭШ мЬ†мЧ≠мЧР мЪ∞мД†мИЬмЬДмЭШ мГБмЬДлУ±кЄЙмЭі нОЄм§СлПЉ мЮИмЧИмЬЉл©∞, мµЬкЈЉ мЭі мЭЉлМАмЭШ лМАкЈЬл™® нЩНмИШнФЉнХіл•Љ к≥†л†§нХШл©і мЭЉл¶ђк∞А мЮИлКФ к≤∞к≥ЉлЭЉ мВђл£МлРЬлЛ§. нХШмІАлІМ, мЭЄкЈЉмЧР м°імЮђнХШлКФ 100718 мЬ†мЧ≠мЭА мЪ∞мД†мИЬмЬДк∞А лВЃк≤М м±Ем†ХмЭі лРШмЧИмЬЉл©∞ мЭілКФ мЬ†мЧ≠лВімЧР мЮРмЧ∞нЬімЦСл¶ЉмЭД лєДл°ѓнХЬ мЧђлЯђ мЛЬмД§мЭі м°імЮђнХШлКФ л∞Ф, мЭі мЭЉлМАмЭШ лПДмЛЬк≥ДнЪН л∞П кіАл¶ђмЧР лФ∞л•Є к≤∞к≥ЉлЭЉ нМРлЛ®лРЬлЛ§.
(2) мЪ∞мД†мИЬмЬД 1~10мЬДкґМмЧР мЖНнХі мЮИлКФ мЬ†мЧ≠лУ§мЭА мєШмИШ мВђмЧЕмЛЬлВШл¶ђмШ§к∞А мІДнЦЙлР®мЧР лФ∞лЭЉ кЄ∞м°імЭШ нЩНмИШмЈ®мХљмД±мЭі лЖТмЭА мЬ†мЧ≠мЭШ мЈ®мХљмД± к∞ЬмД† нЪ®к≥ЉмЩА нХ®кїШ мЬ†мЧ≠ м†Дл∞ШмЧР к±Єм≥Р мЈ®мХљмД± лґИкЈ†нШХмЭШ к∞РмЖМнЪ®к≥Љл•Љ л≥імШАлЛ§. нХЬ мШИл°Ь, кЄ∞м°імЧР мЪ∞мД†мИЬмЬД 1мЬДмШАлНШ 100712 мЬ†мЧ≠мЭА к∞ЬмИШмЬ®к≥Љ м†Ьл∞©м†ХлєДмЬ®мЭі 30% к∞ЬмД†лРРмЭД лХМ, нЩНмИШ мЈ®мХљмД± мІАмИШк∞А 0.19к∞РмЖМнХШмШАмЬЉл©∞, мЭілКФ нШДмЮђмЭШ мЪ∞мД†мИЬмЬД кЄ∞м§АмЬЉл°Ь мХљ 14мЬДмЧР нХілЛєлРШлКФ мИШмєШмЭілЛ§. лЛ§лІМ, нЦ•нЫДмЧРлКФ мєШмИШ мВђмЧЕмЭі нХДмЪФнХЬ нЩНмИШ мЈ®мХљмД± мІАмИШмЭШ кЄ∞м§Ам†РмЭД лІИ놮нХШмЧђ мєШмИШ мВђмЧЕмЭі нХДмЪФ мЧЖлКФ мЬ†мЧ≠мЭД м†ЬмЩЄнХЬ нЫД, мЪ∞мД†мИЬмЬДл•Љ мЮђмВ∞м†ХнХШлКФ мЧ∞кµђк∞А мґФк∞Ам†БмЬЉл°Ь мИШнЦЙлРШмЦімХЉ нХ† к≤ГмЭілЛ§.