열차하중 하 짧은 대구경 봉상보강재의 최적 배치간격에 대한 수치해석적 검토
Numerical Analysis on the Optimum Spacing of a Short and Large Diameter Soil Nailing System Under Railway Load
Article information
Abstract
도심지 기존 시설물 인접굴착 및 보강 시 공간 부족과 새로운 공간 창출을 위하여 불가피하게 연직굴착이 필요한 경우가 있다. 본 연구에서는 대구경 봉상보강재를 적용하여 철도 성토체에 대한 연직 굴착과 보강을 실시할 경우 성토체 및 보강재의 거동을 3차원 수치해석을 통하여 분석하였다. 성토체 높이별로 직경 0.4 m인 대구경 봉상보강재의 설치 간격을 1 m, 2 m, 3 m로 변화시켜 가면서 해석을 수행하였고 각 해석 조건에 대하여 벽체상단의 수평 및 연직 변위량, 보강재 연직 침하량과 축응력을 비교하였다. 그 결과 보강재 간격이 3 m일 경우 벽체 수평변위가 급격히 증가하는 경향을 보였고, 보강재 축응력도 허용값을 초과하는 결과를 도출하였다. 따라서 성토체의 연직굴착에 따른 안정성과 경제성 측면을 고려할 때, 보강재의 최적 설치간격은 2 m가 적합할 것으로 판단되었다.
Trans Abstract
There are necessities of vertical excavation to reduce construction areas and make new spaces in urban area. In this study, 3 dimensional numerical analysis is conducted to assess the behaviour of the embankment with vertical excavation and a short and large diameter soil nailing reinforcement system. The spacing of soil nails are 1 m, 2 m, and 3 m, though the diameter is fixed as 40 cm. Lateral and vertical displacement at the top of wall, vertical displacement and axial stress are also obtained and analyzed. Consequently, lateral displacement at the top of wall increases sharply and tensile stress of soil nail excesses the allowable limit at the nail spacing of 3 m. Therefore, we concluded that the optimum spacing of a short and large diameter soil nailing system could be around 2m at the aspects of safety and cost efficiency for excavation and reinforcement of embankment.
1. 서 론
철도는 장거리, 대량 운송수단으로서 안전성 및 대량 수송성, 정시성이 높은 중요한 사회 기반시설이다. 따라서 교통수단으로서의 중요성과 기여도가 높으며 이로 인하여 철도차량 뿐만 아니라 이를 지지하는 하부노반 구조물의 중요성도 매우 크다. 특히 철도노반은 고속으로 운행하는 높은 중량의 철도 차량을 일차적으로 지지하는 선상 구조물로서 침하와 같은 변형에 안정하도록 설계, 시공하여야 한다. 그러나 도시 집중화로 인한 도심지 공간 활용의 필요성 등의 이유로 불가피하게 철도노반 주변 인접공사 및 성토사면에 대한 연직굴착이 필요한 경우가 증가하고 있다.
이와 같은 경우 철도노반의 안정성을 위하여 지반보강이 반드시 필요하게 되며 쏘일 네일링, 어스앵커, 보강토 옹벽 등 여러 가지 지반보강 방법들이 개발되어 있다. 이 중 쏘일 네일링은 1970 년대 이후 임시 또는 영구 보강재로서 토압저항, 언디피닝, 사면안정 등 여러 영역에서 적용되고 있다(Rashid et al., 2013). Rashid et al. (2013)은 2차원 유한요소해석 및 유한차분 해석을 통하여 12 m 높이의 흙막이 벽체에 대한 보강을 수치해석적으로 검토하였다. 그 결과 해석방법별 변위는 유사하게 나타났으며 전면벽체의 최대 연직변위량은 유한요소해석 결과가 계측결과와 가까운 값으로 도출되었으며, 안전율도 거의 동일한 결과를 얻었다. Yang et al. (2005)은 프리스트레스 앵커, 그라우팅 파일, 마이크로파일 등을 결합한 복합 쏘일 네일링 공법을 개발하여 대심도 굴착에서의 적용 가능성을 확인하였다. Zhu and Li (2005)은 기초 굴착시 쏘일 네일링으로 보강되는 지반에서 쏘일 네일링으로 인한 보강 효과를 해석하기 위하여 안전율과 원호 파괴면과의 관계 함수를 도출하고 실제 사례에 적용하였다. Qin et al. (2005)은 쏘일 네일링의 접촉면 요소를 고려하고 탄성보 모델을 활용하여 쏘일 네일링을 해석하기 위한 유한요소해석 프로그램을 개발하여 실제 사례에 적용하였다. Fan and Luo (2008)는 사면안정을 위한 쏘일 네일링의 최적 형태를 결정하기 위하여 다양한 조건에서의 수치해석을 수행하였다. 그 결과 사면 각도가 작아질수록 수평면에 대한 쏘일 네일링의 각도는 증가하며 전체적인 사면 안정에는 사면 하부 1/3 지점 이하에 시공된 쏘일 네일링의 기여도가 큰 것을 파악하였다.
이와 같이 쏘일 네일링의 형상, 굴착면 또는 성토면의 각도를 매개변수로 하는 최근의 연구에서 다양한 조건에서의 거동 특성을 분석할 수 있는 수치해석적 접근이 널리 활용되고 있다. 본 연구에서는 기존에 개발된 지반보강 방법의 단점을 보완하기 위하여 새로이 개발된 대구경 인장 심재를 갖는 봉상보강재를 이용한 연직굴착 공법에 대하여 3차원 수치해석을 통하여 성토체 높이별 거동특성을 분석하고 보강재의 시공성과 경제성을 확보할 수 있는 최적 설치간격을 검토하였다.
2. 해석 조건
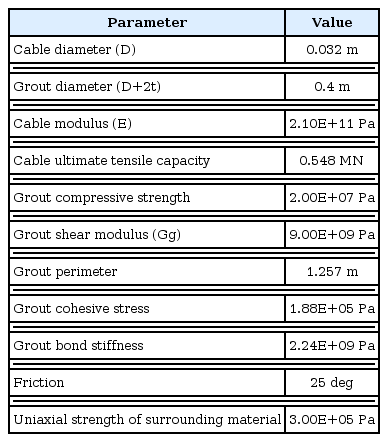
운행중인 철노노반의 법면 굴착 및 보강 시 변형량을 최소화하고 안전성을 확보하기 위한 목적으로 대구경 봉상보강재를 고안하였다. 이와 같이 철도하중을 받고 있는 성토사면을 연직으로 절토할 경우에 대한 대구경 봉상보강재의 설치 간격을 분류하고 성토사면의 높이를 3 m, 6 m, 9 m로 구분하여 각 조건별로 3차원 유한차분해석법에 의한 수치해석을 수행하였다. 그 결과를 분석하기 위하여 전면벽체 수평 및 연직변위량, 최상단 보강재 의 연직변위량, 최상단 보강재 축응력 등을 검토하였다. 본 연구에 적용된 전체적인 해석 조건은 Table 1과 같다. 지반은 변형률에 따라 탄성-완전소성 거동을 모사할 수 있는 Mohr-Coulomb 탄소성 모델을 적용하였고, 보강재는 케이블 요소를 적용한 탄성모델을 적용하였다.
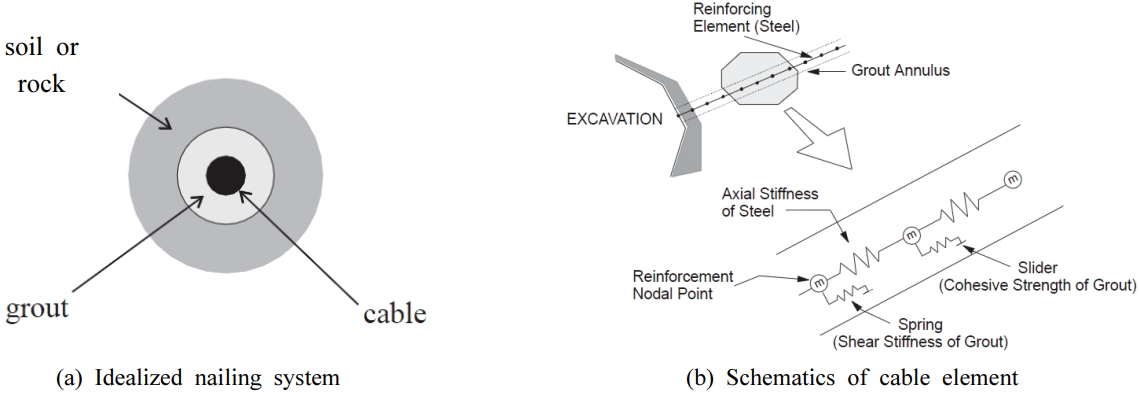
쏘일 네일링의 보강재 강선은 세장비가 크고 휨강성이 상대적으로 작아 무시할 수 있으므로 안전측 해석을 위하여 보강재 자체에 발생하는 모멘트는 해석 시 고려하지 않았다(FHWA, 1998). 따라서 수치해석 시 보강재 강선은 상용프로그램에서 제공하고 있는 구조부재(structural element) 중 케이블 요소(cable element)를 적용하였다. 케이블 요소는 입력변수에 내부 강봉과 주변지반과의 접촉면(interface) 변수들을 고려할 수 있으며 그 적용 개념은 다음 Fig. 1과 같다.
수치해석에 적용할 그라우트 물성값은 기존 연구결과를 활용하여 결정할 수 있다(Kwak and Kim, 2016). 그라우트의 물성값을 정확하게 산정하는 것은 어려우나 그라우트를 탄성-완전 소성체로 가정하면 그라우트에 작용하는 전단력은 그라우트의 강성과 상대변위의 곱으로 구할 수 있다. 그라우트의 강성은 쏘일 내일링 내부 강선에 대한 인발시험을 통해 구할 수 있으나 Eq. (1) (John and Dillen, 1983)을 통하여 해석적으로 계산할 수 있다.
여기서, τG는 강선에 작용하는 전단응력, ∆u는 접촉면 주변 재료와 구조요소와의 상대변위, Gg는 그라우트의 전단탄성계수, D는 강선의 직경, 그리고 t는 강선 주위 그라우트재의 두께이다. 본 수치해석에 적용한 그라우팅재에 대한 스프링 강성 산정 식은 Eq. (2)와 같다(Itasca Consulting Group, 2005).
또한, 그라우트에 작용하는 부착강도(cg)는 Eq. (3)으로 구한 값을 적용하였다.
여기서, τpeak는 최대 전단강도이며 주위지반과 그라우트재의 일축압축강도 중 작은 값의 절반을 적용하였다. 본 연구에서는 쏘일 네일링 그라우트를 포함한 직경을 증가시켜 네일링의 시공 개수를 합리적으로 저감시키고자 직경 40 cm로 고려하였다. 해석에 적용된 케이블 요소의 단면은 Fig. 2와 같다.
여기서, D는 보강재 강선의 직경, Dg는 전체 그라우트의 직경을 나타낸다. Tables 2 와 3에서는 해석에 적용된 케이블 요소의 물성과 입력 지반정수를 나타내었다.
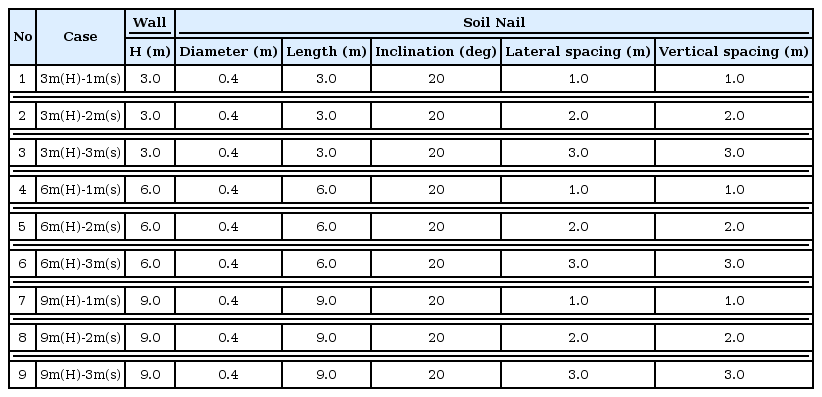
대상 노반이 공용중인 철도 성토사면으로 지하수위는 고려하지 않았고, 성토체 높이를 3 m, 6 m, 9 m로 구분하여 해석 영역을 구성하였다. 각 높이별로 보강재의 수평 및 수직 간격을 1 m, 2 m, 3 m로 적용하여 각각 해석을 수행하여 그 결과를 비교하였다. 전체 해석 케이스는 Table 4와 같고, 해석 단면도는 Fig. 3과 같다. 적용 보강재길이는 협소한 공간에서의 적용이 가능하도록 높이와 동일한 100 %H의 짧은 보강재로 결정하였다.
보강재 간격은 성토체 높이에 따라 해석 경계영역과 대칭을 이루도록 적절히 조절하여 배치하였으며 성토체 면적 대비 쏘일 네일링의 면적비는 다음 Table 5와 같다.
성토체 상부에 재하되는 철도 노반압력은 철도설계기준(Korea Railway Network Authority, 2013)에 따라 Fig. 4와 같이 적용하였다.
3. 해석 결과 및 분석
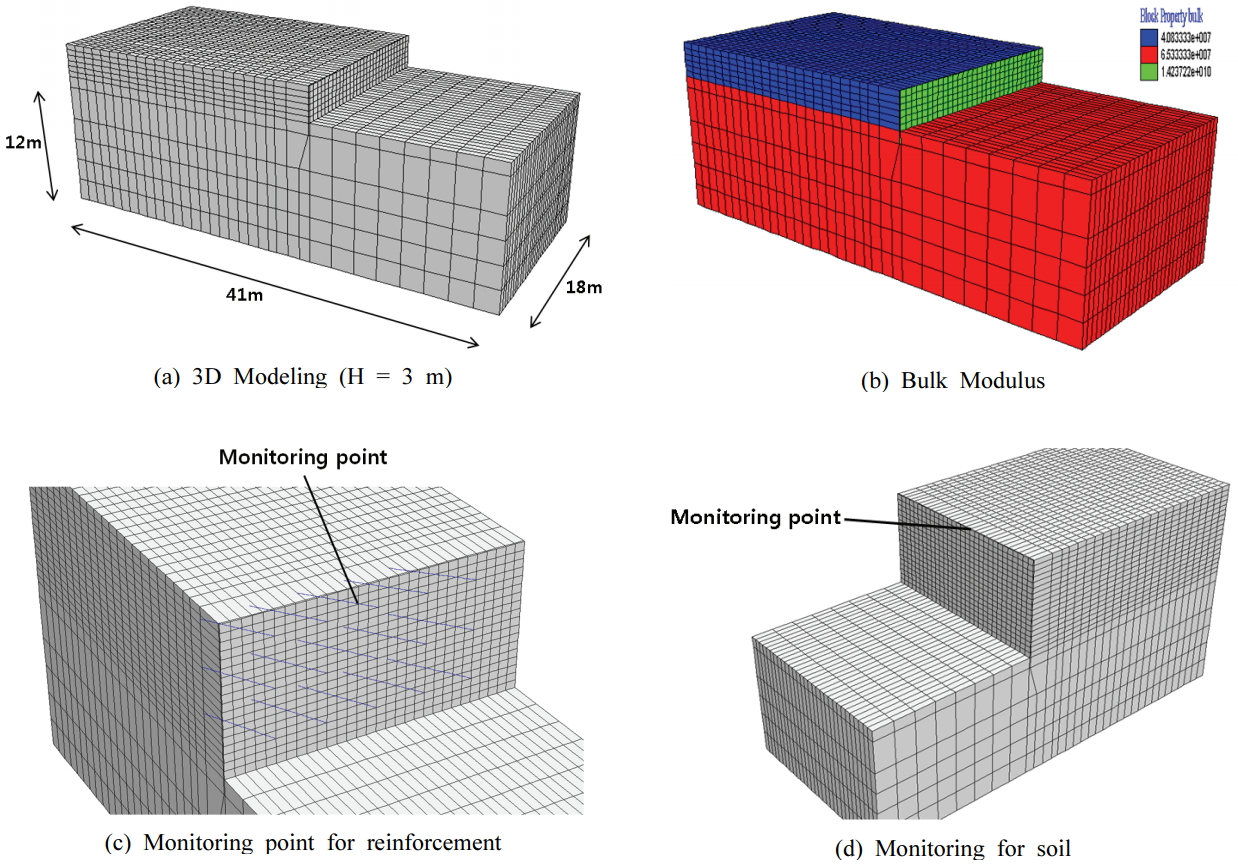
3차원 유한차분해석을 위한 모델링 결과는 Figs. 5 (a), (b)와 같다. 보강재와 지반에 대한 응답값의 모니터링 위치는 Figs. 5 (c), (d)와 같이 최상단 보강재 중간 위치 보강재의 벽체로부터 1.5 m 이격된 지점과, 벽체 최상단 중간지점으로 설정하였다.
본 해석에서는 대구경 봉상보강재의 최적 보강조건 중 보강재 간격에 따른 특성을 분석하기 위하여 보강재 간격을 조정하면서 해석을 수행하였다. 먼저 벽체 상단의 수평변위를 해석단계에 따라 도시한 결과는 Fig. 6과 같다.
벽체 상단의 최대 수평변위는 높이 9 m, 보강재 간격 3 m에서 7.81 mm로 나타났다. 보강재 간격 증가에 따른 수평변위 발생 경향을 살펴보면 벽체높이 3 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 21.3 % 증가하였으나 간격 3 m 적용 시 1 m 적용 시에 비해 최대 161.3 % 만큼 급격하게 증가하였다. 벽체높이 6 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 69.9 % 증가하였으나 간격 3 m 적용 시 1 m 적용 시와 비교하여 최대 248.8 % 만큼 급격하게 증가하였다. 벽체높이 9 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 92.9 % 증가하였으나 간격 3 m 적용 시 1 m 적용 시와 비교하여 최대 188.7 % 만큼 크게 증가하였다. 즉 보강재 간격이 커질수록 벽체상단 수평변위의 증가폭이 커지며 이는 벽체 높이가 높을수록 더 급격히 큰 값으로 증가하는 것으로 나타났다.
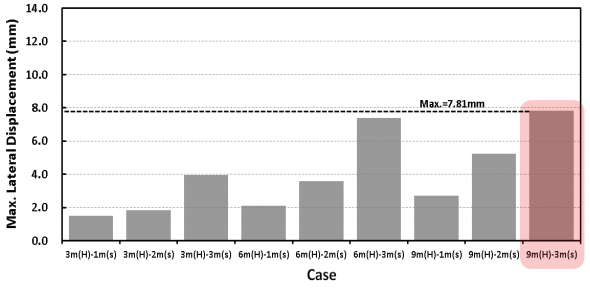
또한 벽체 높이가 증가할수록 보강재 개수가 증가함에도 불구하고 전체 수평 변위량은 증가하므로 성토체의 토압증가량이 성토체 높이에 더 크게 영향을 받는 경향을 나타내었다. 모든 해석 케이스에 대하여 벽체 상단의 최대 수평변위량을 도시하면 Fig. 7과 같다. 허용 수평변위량은 철도설계기준(2013)의 콘크리트 전면벽체를 갖는 보강토 옹벽 기준 준용 시 0.6 %H로, 본 해석에서의 최대 발생 수평변위량은 7.81 mm로 허용값인 54 mm의 14.5% 수준으로 허용범위 이내였다. 전체적으로 보면 보강재 간격이 3 m로 증가 시 수평 변위량이 크게 증가하는 형태를 보였고, 전체 벽체면적 대비 보강재 단면적의 비율이 동일하더라도 보강재 간격이 3 m 로 커져 보강재 개수가 줄어들 경우 벽체 안정성을 현저하게 저하시킬 수 있을 것으로 판단된다.
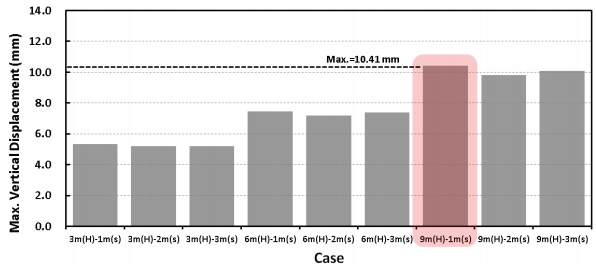
Fig. 8은 벽체 상단의 연직변위를 해석단계에 따라 도시한 결과이다. 벽체 상단의 최대 연직변위는 높이 9 m, 보강재 간격 1 m에서 10.41 mm로 나타났다. 그러나 벽체 높이가 동일할 경우 보강재 간격에 따른 최대 연직변위의 차이는 벽체 높이 9 m, 보강재 간격 2 m인 경우 간격 1 m와 비교하여 최대 5.7 % 감소하는 것으로서 나타났다. 반면 벽체의 연직변위는 보강재가 1 m 간격일 경우 벽체 높이가 3 m에서 6 m로 증가 시 높이 6 m에서 39.1 % 증가하고, 높이 6 m에서 9 m로 증가 시 높이 9 m에서 39.9 % 증가하여 벽체 높이 증가에 따라 약 40 % 정도 증가함을 알 수 있었다. Fig. 9는 모든 해석 케이스에 대하여 벽체 상단의 최대 연직변위를 도시한 결과이다.
Fig. 10은 상부 철도하중 재하면에서 가장 가까운 최상단 보강재의 연직변위를 해석단계에 따라 도시한 결과이다. 보강재 연직변위 측정점은 벽체 중앙부로부터 배면방향으로 1.5 m 지점이다. 해석 결과 최상단 보강재의 최대 연직변위는 높이 9 m, 보강재 간격 3 m에서 16.05 mm로 나타났다. 보강재 간격 증가에 따른 보강재 연직변위 발생 경향을 살펴보면 벽체높이 3 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 5.0 % 증가하였으나, 간격 3 m 적용 시 1 m 적용 시와 비교하여 최대 10.3 % 만큼 소폭 감소하였다. 이는 보강재 간격 1 m 및 2 m일 경우 보강재 배치상 성토체 상단 지표면으로부터의 거리가 0.5 m이나, 보강재 간격 3 m일 경우 거리가 1.5 m로 증가하기 때문으로 판단된다.
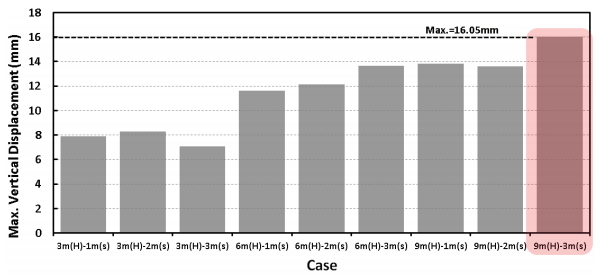
벽체높이 6 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 4.4 % 증가하였고 간격 3 m 적용 시 1 m 적용 시와 비교하여 최대 17.4 % 증가하였다. 벽체높이 9 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 1.6 % 소폭 감소하였으나 간격 3 m 적용 시 1 m 적용 시와 비교하여 16.2 % 증가하였다. 특히 벽체높이 9 m일 경우 보강재 간격 1 m의 최상단 보강재의 토피고는 0.5 m이나, 3 m에서는 1.5 m로 크게 증가함에도 불구하고 보강재 간격 3 m에서 최대 연직변위량이 발생한 것은 보강재 간격을 3 m로 적용 시 보강재 자체의 연직변위량이 과다하게 발생함을 의미하므로 역시 성토체 전체 안정성에 불리한 결과를 초래함을 알 수 있다. Fig. 11은 모든 해석 케이스에 대하여 최상단 보강재의 최대 연직변위를 도시한 결과이다.
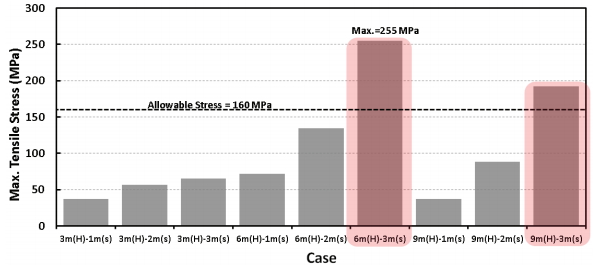
상부 철도하중 재하면에서 가장 가까운 최상단 보강재에 발생하는 축응력을 해석단계에 따라 도시한 결과는 Fig. 12와 같다. 보강재 축력 측점은 연직변위 측점과 동일하게 벽체 중앙부로부터 배면방향으로 1.5 m 지점이다. 해석 결과 최상단 보강재의 최대 축응력은 높이 6 m, 보강재 간격 3 m에서 255.3 MPa로 나타났다. 보강재 간격 증가에 따른 보강재 축응력 발생 경향을 살펴보면 벽체높이 3 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 50.5 % 증가하였고 간격 3 m 적용 시 1 m 적용시와 비교하여 74.6 % 증가하였다. 벽체높이 6 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 88.0 % 증가하였고 간격 3 m 적용 시 1 m 적용 시와 비교하여 최대 256.6 % 증가하였다. 벽체높이 9 m일 경우 간격 2 m 적용 시 간격 1 m와 비교하여 137.6 %로 크게 증가하였고 간격 3 m 적용 시 1 m 적용 시와 비교하여 417.2 % 만큼 최대 폭으로 증가하였다. 보강재 내부의 강선은 SD35 기준 허용인장강도를 160 MPa로 가정하면 벽체높이 6 m, 보강재 간격 3 m인 경우와 벽체높이 9 m, 보강재 간격 3 m인 경우는 보강재 자체에서 인장파괴가 발생하는 결과가 도출되므로 보강재 간격 3 m는 안정성에 문제가 있을 것으로 판단된다. Fig. 13에서는 모든 해석케이스에 대하여 최상단 보강재의 최대 축응력을 도시한 결과이다.
최종 굴착단계에서 발생한 소성 영역을 도시하면 다음 Fig. 14와 같다. 보강재 간격 2 m의 경우 보강재 배면은 탄성영역 범위에 있고 소성영역은 발생하지 않으므로 전체적으로 소성파괴 위험은 없는 것으로 판단되었다.
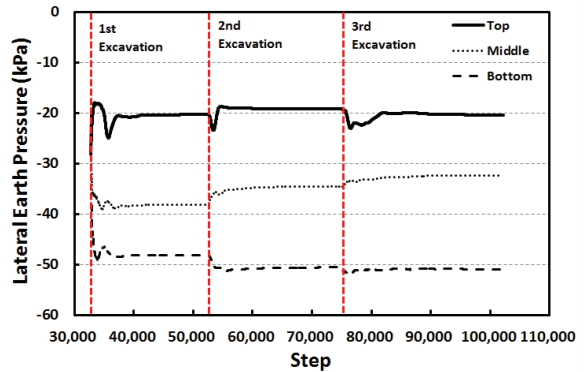
대구경 봉상보강재 설치 시 벽체(H = 6 m) 배면의 토압을 벽체 상단, 중단 및 하단부에서 굴착 단계별로 각각 산정한 결과는 Fig. 15와 같다.
벽체 배면토압은 심도가 가장 깊은 하단부에서 최대 51.8 kPa로 가장 크게 산정되었고 상단부에서 28.6 kPa 로 가장 작게 산정되었다. 굴착 단계별 토압 변화를 살펴보면, 벽체 상단 및 중단에서 굴착 시 일시적으로 토압이 감소하나 철도하중의 영향으로 다시 회복되는 경향을 보였다. 벽체 하단에서는 굴착 단계에 따라 토압이 소폭 감소하나, 봉상보강재 설치로 인하여 그 감소폭은 10% 이내로 크지 않았다. 벽체 깊이별 배면토압의 분포는 Fig. 16과 같이 Rankine 토압 분포와 유사하게 나타났다.
4. 결 론
일반적인 쏘일네일링 공법과 비교하여 짧으면서도 대구경인 봉상보강재를 이용하여 운영중인 철도노반을 연직 굴착 보강하는 기술에 대하여 보강재 직경 40 cm, 설치각도 20 도, 보강재 길이는 벽체높이와 동일한 조건에서 벽체 높이별(3 m, 6 m, 9 m) 최적 보강간격을 3차원 수치해석을 통하여 검토한 결과는 다음과 같다.
(1) 보강재 간격 증가에 따른 벽체 상단의 수평변위 발생 경향을 분석한 결과, 보강재 간격이 커질수록 벽체 상단 수평변위의 증가폭이 커지며 이는 벽체 높이가 높을수록 더 급격히 크게 증가하는 것으로 산정되었다. 현 해석조건 하에서 발생한 최대 수평변위량은 철도설계기준(2013)의 허용범위 기준을 만족하나, 보강재 간격을 3 m로 증가하는 경우 벽체 상단의 수평변위량이 크게 증가하는 거동을 보이므로 보강재 설치에도 불구하고 벽체의 안정성은 확보하기 어려울 수 있을 것으로 판단되었다.
(2) 보강재 간격 증가에 따른 벽체 상단의 최대 연직변위 발생 경향을 분석한 결과, 최대 연직변위는 높이 9 m, 보강재 간격 1 m에서 10.41 mm로 나타났다. 그러나 벽체 높이가 동일할 경우 보강재 간격에 따른 최대연직변위의 차이는 최대 5.7 %로서 미소하게 나타나므로 벽체 연직변위는 보강재 간격보다 성토체 높이에 주로 영향을 받음을 알 수 있었다.
(3) 상부 철도하중 재하면에서 가장 가까운 최상단 보강재의 연직변위를 분석한 결과, 최대 연직변위는 높이 9 m, 보강재 간격 3 m에서 16.05 mm로 나타났다. 성토체 높이가 증가할 경우 보강재 간격을 3 m로 적용 시 토피고가 커짐에도 불구하고 보강재 자체의 연직변위량이 과다하게 발생하였다.
(4) 최상단 보강재의 축응력을 분석한 결과, 최대 축응력은 높이 6 m, 보강재 간격 3 m에서 255.3 MPa로 나타났다. 벽체높이 6 m이고 보강재 간격 3 m인 경우와 벽체높이 9 m 이고 보강재 간격 3 m인 경우 보강재 자체에서 인장파괴가 발생하는 결과가 도출되어 보강재 간격 3 m 는 보강재 안정성에 문제가 있을 것으로 판단되었다.
(5) 벽체 배면토압에 대한 검토 결과 Rankine 토압 분포와 유사하게 상단부에서 가장 작고, 하단부에서 가장 크게 산정되는 경향을 나타내었다.
상기의 조건 하에서 안정성과 경제성 측면을 고려한 동 해석조건하에서의 대구경 봉상보강재의 최적 설치간격은 2 m 수준이 적정할 것으로 판단되며 향 후 현장 시공조건 변화 등을 고려하여 최적 설치간격을 결정할 필요가 있을 것이다.
Acknowledgements
본 연구는 한국철도기술연구원 주요연구사업의 연구비지원(“도심지 철도 선로법면 제거를 통한 용지 활용 기술개발” 연구사업)에 의해 수행되었습니다.