|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(5); 2018 > Article |
|
Abstract
In this study, the hydrological drought index was calculated using Modified Water Supply Index (MSWSI). The quantified value corresponding to MSWSI -1 was estimated from the relationship between drought index and input factor. The target area was the 3006 basin where precipitation, river flow, and dam inflow have been recorded for 21 years (January 1997 to August 2017). The drought index was estimated over two time intervals, one month and three months moving average. The quantitative values were estimated for each month and for each input data using a linear regression equation. The monthly MSWSI showed considerable variability between the drought and wet conditions. And also the coefficient of determination between drought index and each input data revealed no correlation. To improve the coefficient of determination and to derive the appropriate linear regression constants, the ranking by each factor and the rank difference between MSWSI drought index and each input factor were calculated. The applied rank difference was estimated to be within 15% and 30%. Re-quantifying the available water resources is expected to be useful in preparing water use policy.
요지
본 연구에서는 수문학적 가뭄지수인 Modified Water Supply Index (MSWSI)를 적용하여 가뭄분석을 수행하였고, 산정된 가뭄지수와 입력인자의 관계 분석을 통해 약한 가뭄과 정상상태를 구분 기준인 MSWSI -1에 해당하는 입력 인자별 강우량, 하천유량, 댐 유입량의 가뭄을 유발하는 기준에 대한 정량화된 값을 산정하고자 하였다. 대상유역은 강수, 하천유량 및 댐 유입량을 입력인자로 갖고, 21년 248개월의 기간 자료를 보유한 중권역 3006 지점으로 하였다. 가뭄지수의 시간 단위는 월 단위 및 3개월 이동평균을 적용하였고, 가뭄지수와 각각의 입력인자를 대응시켜 선형회귀식을 적용하고자 하였으며, 이를 위해 회귀상수를 도출하였다. 월 단위 회귀식 산정결과 일시적인 수분 부족(과잉)이 이전 습윤(가뭄) 상태 전환에 상당한 영향을 갖지 않을 수 있음에 따라 유의한 결정계수를 갖지 못하는 것으로 분석된 반면에 3개월 이동평균의 경우에는 결정계수가 높게 분석되었다. 월 단위 자료의 상이한 분포를 나타내는 자료를 제거를 통한 회귀상수 도출을 위해 MSWSI와 각 입력 인자의 순위 도출 및 순위 차이를 적용하였다. 순위차이를 통해 전자료들 중에서 15% 및 30% 이내의 유의성을 갖는 자료를 추출하고, 결정계수를 및 회귀상수를 도출하였으며, 월 단위 및 3개월 이동평균에 대한 정량화 결과를 월별/인자별 비교 검토를 수행하였다. 본 연구의 각 인자별 가용수자원 공급량 산정을 통해 정량화된 가뭄 기준 값의 산정결과는 최근 빈번한 발생을 갖는 가뭄에 따른 물이용 정책을 마련하는데 있어 높은 활용성을 가질 것으로 판단하였다.
기후변화로 인한 전 지구의 기온 상승은 강수량의 빈도와 규모에 영향을 미치며, 장래에는 가뭄과 관련한 가용수자원의 공급은 상당한 감소 전망이 보임에 따라 물 부족에 대비할 수 있는 합리적인 정책 마련이 필요하다(IPCC, 2007).
유역의 지속적인 물 공급 부족으로 정의되는 가뭄은 원인, 기준 및 영향관계를 고려하여 기상학적 가뭄, 수문학적 가뭄, 농업적 가뭄 등으로 구분되어 정의 된다. 이 중에서 수문학적 가뭄은 유역의 수문순환 관계에 따른 유용 가능한 가용수자원 이용 측면에서 가뭄을 평가하는 것으로 가뭄 평가에 있어 수문학적 변수의 선택에 따라 다양성 있는 수문학적 가뭄 평가 기법 연구가 이루어지고 있다(Sung and Chung, 2014a, 2014b; Jeong et al., 2017).
Palmer (1965)는 수문학적 가뭄평가를 위해 강수량, 하천유량, 토양수분량, 증발산량을 이용하는 Palmer Hydrological Drought Index (PHDI)를 제안하였고, Hollinger et al. (1993)은 토양수분 기준으로 Soil Moisture Drought Index (SMDI) 가뭄지수를 개발하였다. Stahl (2001)은 동일지역 하천유량 부족분의 가뭄지수 평가인 Regional Streamflow Deficiency Index (RSDI)를 제시한 바 있고, Shafer and Dezman (1982)는 하천유량 외에도 강수량, 저류량, 융설량을 고려한 여러 가용수자원에 따른 가뭄 분석 기법으로 Surface Water Supply Index (SWSI)를 제시한 바 있다. 이러한 다양한 수문학적 가뭄평가 기법들 중에서 유역의 수문순환을 고려하는 SWSI 기법을 국내 실정에 맞게 보완하여 강수량, 하천유량, 댐 유입량 등의 입력 자료로 갖는 MSWSI 기법을 제시하였다(Kwon et al., 2006, Jeong et al., 2017).
상기 제시된 여러 수문학적 가뭄 평가 기법들은 통계적인 기법을 활용하여 분석 절차 내에서 지수화를 통한 가뭄 및 습윤 상태의 분류가 이루어지고 있으며, Palmer Drought Severity Index (PDSI)와 동일한 구분기준을 갖는 MSWSI의 분류기준에서는 -1 이하는 가뭄, -1과 1 사이는 정상 상태, 1보다 큰 경우는 습윤 상태로 구분하여 제시하고 있다(Jang et al., 2016). 이러한 가뭄의 범주는 월 단위 가뭄지수를 통한 가뭄상태를 평가하는데 있어 유용성을 갖는 반면에 가뭄정보를 활용한 정책 반영에는 한계를 나타낼 수 있다. 가뭄지수는 가뭄 상태의 표현 및 미래 가뭄 예측에 있어 유용성을 갖지만 그 자체의 지수화된 정보는 저수지 및 댐 등을 관리하는 관리자 및 가뭄과 관련한 정책 결정자 등이 받아들이기에는 어려움이 있으며, 이를 보다 구체화된 수치 정보 등을 통해 저수지 및 댐 운영 등의 합리적인 의사 전달 체계 및 관리 체계가 마련될 수 있도록 정량화된 값으로의 제시에 필요성을 갖는다. Kwon et al. (2007)은 MSWSI와 지하수위의 상관분석을 통해 주단위 지하수위 임계값의 산정을 제시하였으며, 이를 위해 두 변수간의 선형회귀식을 적용한 바 있다.
본 연구에서는 가뭄 및 습윤 상태와 관련한 보다 구체화된 가뭄 정보 전달을 위해 지수화된 가뭄지수를 정량화된 값으로의 변환과정에 대한 검토를 수행하고자 하였다. 분석을 위한 수문학적 가뭄지수는 MSWSI를 적용하였고, 월 단위 및 3개월 이동평균에 대한 가뭄지수를 산정하였다. 공간적인 범위는 MSWSI에 따른 댐 유역에 해당하는 대청댐상류 3006지점을 선택하였으며, 자료 기간은 유역의 1997년 1월부터 2017년 8월까지 21년 248개월이 기간자료를 적용하였다.
정량적인 값의 도출은 월별 및 입력 자료별로 검토를 수행하였고, 각각에 대한 회귀식 및 결정계수를 산정하였다. 회귀분석 결과에 대한 결정계수가 유의하지 않은 경우에는 순위 도출 및 순위차를 적용하여 회귀식의 재산정을 수행하였고, 산정된 결과를 토대로 월별 지수에 대응하는 입력자료별 기준 값의 산정을 수행하였다.
본 연구에서는 유역에 가용수자원인 강수량, 하천유량, 댐 유입량을 입력 자료로 하여 MSWSI 가뭄지수를 적용한 수문학적 가뭄 분석을 수행하고, 산정된 결과를 토대로 각 입력 자료별로 가뭄상태를 유발하는 정량화된 기준값을 산정하고자 하였다. 분석을 위한 대상지역은 21개 중권역이 포함되어 있는 금강유역 중에서 수문강수량, 하천유량 및 댐 유입량 자료를 입력인자로 갖는 7개 지역을 일차적으로 선정하였고, 이들 중에서 가장 긴 자료 기간을 보유하고 있는 대청댐 상류 부근에 위치한 중권역 3006 지점을 선정하였다. 대상 지역 입력 자료는 국가수자원관리종합정보시스템(WAMIS)에서 수집된 1997년 1월에서 2017년 8월까지 21년 248개월 기간치 자료를 사용하였다. 인자별 수집 자료에 대한 위치 정보는 Table 1로 나타내었다.
가뭄은 지속적인 시간을 두고 장시간에 걸쳐서 발생되는 물 부족 피해를 의미함에 따라 월 단위를 기본으로 하고, 이동평균을 고려한 단기 및 중장기적인 가뭄분석이 이루어 질 수 있다(Lee et al., 2013; Jeong et al., 2016). 본 연구에서는 월단위의 가뭄지수와 함께 3개월 이동평균을 고려한 가뭄지수를 적용하였고 이동평균 식은 Eq. (1)과 같다.
여기서, m은 이동평균, n은 자료 총 개수, Pi는 월 단위 i번째 입력 값, MAk는 자료의 k번째 해당하는 이동평균 결과 값을 나타낸다.
본 연구에서는 여러 정의의 가뭄평가 중에서 수문학적 가뭄지수에 의한 분석을 수행하였고, 분석기법으로 MSWSI를 적용하였다. MSWSI는 지표수 공급지수에 따른 가뭄평가인 SWSI를 국내의 특성에 맞게 보완한 기법으로 확률개념과 수문인자 간의 비교⋅조합을 이용한 유역 특성과 가뭄의 잠재적인 영향 관계를 분석하는 지수이다(Shafer and Dezman, 1982; Lee et al., 2003; Kwon et al., 2006).
MSWSI의 적용은 유역에 가용수자원 입력 자료의 구성에 따라 강수자료만을 입력인자로 갖는 강수유역, 강수 및 하천 유량을 입력인자로 하는 하천유역 그리고 강수, 하천, 댐 유입량을 입력인자로 갖는 댐 유역 Type I과 하천을 제외한 강수와 댐 유입량을 입력 인자로 하는 댐 유역 Type II로 구분될 수 있다(Jeong et al., 2017).
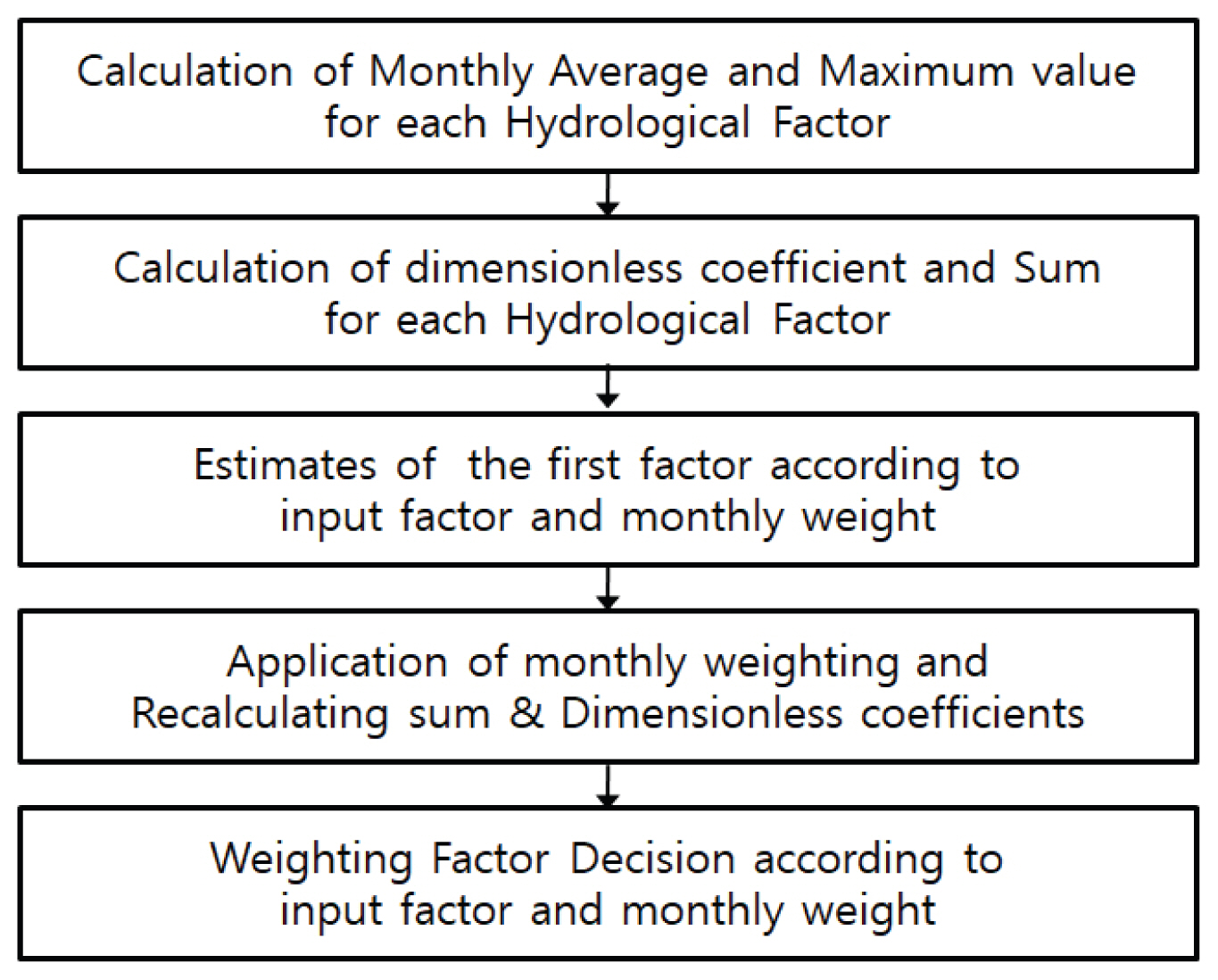
유역 결정 및 이에 따른 입력 자료 수집이 이루어지면, Fig. 2의 절차에 따라 가뭄지수산정이 이루어진다. 이러한 일련의 과정 내에서 각 인자별 가중치 적용이 이루어진다(Jeong et al., 2017).
MSWSI 산정 식은 Eq. (2)와 같다.
여기서, PNpcp
, PNsf
, PNrs
는 각각 강우, 하천유량, 댐 유입량에 대한 비초과확률이며, a, b, c는 각 수문인자의 가중계수이고, pcp, sf, rs는 각각 강수, 하천유출, 댐 저류량 인자를 나타낸다. 가뭄심도 평가는 Table 2에 제시된 값에 의해 9개의 구분 기준을 갖는다.
가뭄정도를 표현하기 위해서 통계적 절차에 따라 유역의 가용수자원 부족 및 과잉에 대한 평가가 이루어지며, Fig. 2의 절차에 따라 해당 월의 가뭄지수화를 통해 가뭄상태의 판정이 이루어진다. 이와 같이 산정된 가뭄지수는 한 개 이상의 입력 자료들의 가중개념이 반영되어 있음에 따라 개별 인자와 가뭄에 대한 상관분석을 수행하고자 하였고, 이러한 과정을 통해 가뭄지수에 해당하는 입력인자별 가뭄을 유발하는 정량화된 기준값의 환산과정을 수행하였다.
선형회귀식은 평면상에 도시된 두 인자간의 증감에 따른 추세 분석 및 선형회귀상수를 도출한다. 통계적인 절차를 통한 유역의 가뭄분석에는 가용수자원이 상향될수록 습윤 상태를 반영하고, 하향될수록 가뭄 상태를 전제할 수 있다. 이러한 전제하에 가용수자원 개별 입력인자에 대응되는 가뭄지수를 두 인자로 상정하고, 두 인자간 선형 회귀상수 산정이 이루어지며, 회귀상수를 이용한 가뭄지수 -1에 해당하는 입력 인자를 구함으로서 인자별 정량화된 값을 산출하고자 하였다.
Eq. (3)은 선형회귀식을 나타내었다(Kwon et al., 2007; Kim et al., 2012).
여기서, M ¯ (I , m)
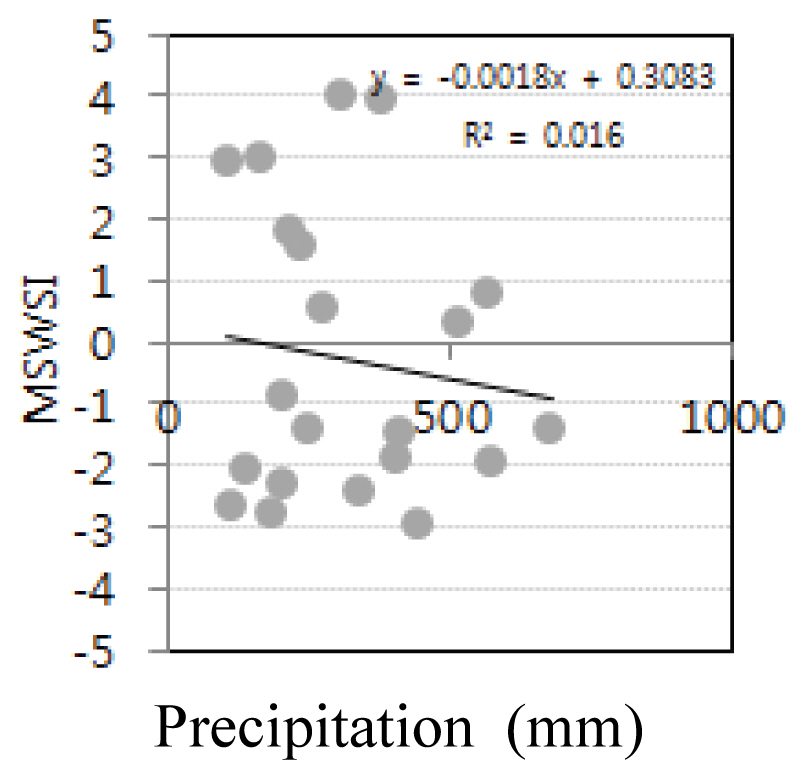
Table 3은 대상지점의 월 단위 자료를 이용한 MSWSI 산정결과들 중에서 연도별 특정한 월에 대한 분석결과를 예시한 것으로 강수량을 x축, MSWSI 지수를 y축으로 하여 Fig. 3으로 도시하였다.
강수량과 가뭄지수를 도시한 결과 자료가 방사형 분포를 보였고, 결정계수가 0.016으로 나타났으며, 추세 또한 음의 방향으로 분석되었다. 가뭄 발생에서 기본적으로 전제될 수 있는 강수량과 가뭄지수의 관계 분석에 있어 가뭄 상태일수록 강수가 부족인 상황을 나타내고, 습윤 상태일수로 과잉되는 상태인 것을 감안하는 경우로 판단할 때, 결과적으로 Fig. 3의 자료 분포는 다소 상이한 결과를 보이는 것으로 판단되었다.
이러한 결과는 가뭄 발생이 단기간 물 공급 부족(과잉) 상태가 장기간 지속되어온 유역의 습윤(가뭄) 상태를 가뭄(습윤)으로 전환시키는데 있어 한계가 있음을 반영하는 결과로 판단되며, Fig. 3의 월 단위 가뭄평가는 해당월의 가뭄상태만을 고려할 뿐, 기준 월 이전상태를 고려하지 못하는 것으로 이해될 수 있다.
앞서 제시된 선형회귀분석을 위해서 Fig. 3의 산정결과를 토대로 해당 월의 수분공급 부족에서 유역 습윤 및 과잉 수분공급에서 유역 가뭄 발생이 된 자료를 제거하고자 하였으며, 이를 위해서 입력인자별 순위도출 및 순위차이 적용을 검토하였다.
앞서 Table 2에 제시된 바와 같이 MSWSI 가뭄 평가의 범례는 0을 기준으로 대칭적이고, 가뭄지수 산정을 위한 통계 분포형이 대칭성을 가지며, 가뭄에 해당하는 분포형 꼬리 부분과 습윤에 해당하는 분포형 머리 부분 또한 대칭적인 구분을 고려하였을 때, 분석된 가뭄지수의 결과가 대칭적인 상태를 가질 것으로 판단될 수 있다.
또한 분석결과가 가질 수 있는 자료의 오차발생의 대칭성 또는 입력량과 가뭄지수간 관계 설정의 오류 상황 발생이 대칭적일 수 있을 것으로 판단되었다. 이러한 오차를 제거하기 위해 회귀분석에 사용되는 두 인자 각각의 순위를 도출하고 두 인자간의 순위차를 적용하여 순위차가 제안되는 일정한 범위를 벗어나는 경우 제거하고자 하였다. 또한 제거된 인자를 제외한 선택된 인자들을 이용해 회귀분석을 수행하고자 하였다.
본 연구에서 적용되는 인자들은 수문학적 가뭄지수 산정에 해당됨에 따라 순위 도출은 MSWSI의 경우 습윤 상태를 상위 순위로 하고 가뭄 상태일수록 하위 순위를 두어 순위도출을 하였고, 가용수자원인 각 입력 자료도 이러한 기준에 따라 입력량이 클수록 상위를 두어 순위를 도출하였다.
본 연구에서는 수문학적 가뭄지수인 MSWSI를 적용하였고, MSWSI 분류상 댐 유역 중권역 3006 지점을 대상으로 분석을 수행하였다. 가뭄지수의 시간단위는 월 단위(Month, M1) 및 3개월 이동평균(3 Months Moving average, MM3)을 적용하였고, 댐 유역 입력 자료인 대청댐유역의 강수, 하천유출량, 댐 유입량을 적용하였다. Fig. 5는 MSWSI를 적용한 수문학적 가뭄지수를 도시하였다. 가뭄의 범례는 앞서 제시한바와 같이 9개 구분기준으로 구분되며, 이를 습윤, 정상 및 가뭄 상태로 구분하여 나타내었고, 1년 12개월을 음영을 두어 1~3월 및 10~12월과 4~9월을 구분하여 나타내었다. 또한 가뭄 발생해는 2001, 2002, 2008, 2009, 2014, 2015년으로 나타내었다(Jeong et al., 2016; Jeong et al., 2017). 이외에도 자료기간이 1월에서 8월까지인 2017년은 가뭄 발생해로 판단하였다.
수문학적 가뭄지수를 산정한 결과 Fig. 5(a)인 월단위에서는 연도별로 가뭄과 습윤의 발생이 반복적인 양상을 보이는 반면에 2003년에서 2010년 사이에서는 가뭄이 습윤보다 발생빈도가 높은 것으로 나타났다. 1년을 4분기로 구분하는 경우에는 강우발생이 상대적으로 적은 1분기(1~3월)와 4분기(10~12월)에서는 대부분의 해에서 가뭄발생 양상을 보이는 반면에 이 시기의 가뭄이 과거의 가뭄 발생해와 정확히 일치성을 보이지는 않는 것으로 판단되었다. 1998-1999년은 가뭄해가 아님에도 불구하고 1998년 4분기에서 1999년 1분기 사이 가뭄발생이 뚜렷한 것으로 나타났다.
이와 달리 여름철을 포함하는 2분기 및 3분기 가뭄발생 지속기간 및 가뭄심도가 가뭄발생해와 연관성을 갖는 것으로 보였으며, 2001~2002년에는 2001년의 여름철 가뭄이 현저함에 따른 가뭄 상태를 나타냈으며, 연이은 해인 2002년은 봄철에 습윤 상태를 보였으나 2분기 가뭄발생에 따라 가뭄 발생해로 분류되었다. 또한 2008~2009년, 2014~ 2015년에는 여름철 가뭄이 확연한 것으로 판단되었다. 이외에 2012년과 2013년의 경우에는 여름철 가뭄 발생을 보였으나 가뭄심도가 다른 가뭄 발생해에 비해 상대적으로 높지 않고, 이전 연도에 가뭄 발생으로 나타나지 않음에 따라 가뭄발생 해는 아닌 것으로 판단되었다.
Fig. 5(b)의 3개월 이동평균에 따른 가뭄지수 산정결과, 분기별로 확연한 구분을 보였으며, 가뭄 발생해로 분류된 해에는 여름철인 2분기 및 3분기에 지속적인 가뭄을 보였고, 가뭄심도는 심한가뭄(Severe Drought) 이상으로 나타났다. 가뭄 발생해별로 보면 2001년은 2002년과 달리 확연한 여름철 가뭄을 보이는 것으로 분석되었고, 2008~2009년과 2014~2015년에는 2015년 봄철 습윤 상태를 제외하고는 전반적인 가뭄 상태로 분석되었다. 이와 달리 2000, 2004~2007년에서는 부분적인 여름철 가뭄상태를 보였고, 가뭄 심도도 다른 가뭄 발생해에 비해서 상대적으로 크지 않은 것으로 분석되었다. 이외에 2017년은 가뭄 발생해로 분류하지는 않았지만 월단위 및 3개월 이동평균 여름철 가뭄 발생 양상에 따라 가뭄해로 분류될 것으로 판단되었다.
앞서 Fig. 3에 대한 분석에서는 강수량과 가뭄지수의 도시결과 두 인자가 선형성을 갖지 않는 것으로 나타났다. 이러한 결과는 가뭄(습윤) 상태가 지속되는 경우 일시적인 수분 유입(부족)이 이전의 지속적인 상태반영에 큰 기여를 갖지 않을 수도 있는 것으로 판단되었으며, 상태 반영이 제대로 이루어지지 않은 자료를 선별 및 제거하기 위하여 각 인자별 순위도출 및 순위차를 적용한 분석을 수행하였다.
순위 도출은 습윤 상태를 상위순위(가뭄상태를 하위순위)로 하여 가뭄지수가 큰 경우와 가용수자원의 각 입력 자료별 값이 클수록 높은 순위를 갖도록 하였다.
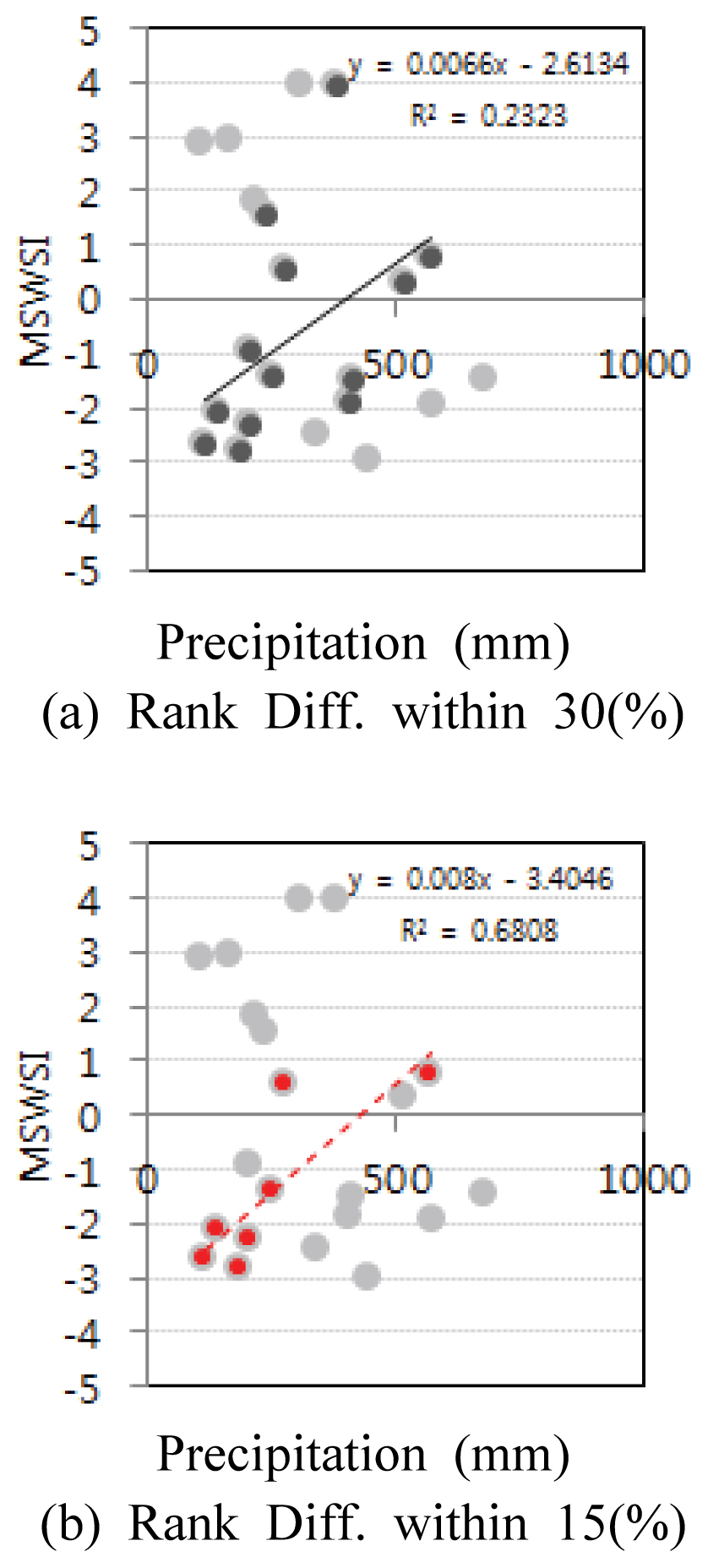
Table 4는 Fig. 3의 강우량 자료 및 가뭄지수에 대한 순위를 도출하고, 두 인자간의 순위차를 적용한 결과를 나타내었다. Fig. 6은 순위차이에 따른 15% 및 30% 이내의 자료를 각각 추출하여 도시 및 회귀분석 결과를 나타내었다. 분석결과 순위차 30% 이내인 Fig. 6(a)에서는 도시적으로 방사형 분포를 보였으며, 결정계수는 0.23으로 분석되었다. 이와 달리 순위차 15% 이내의 자료를 추출하여 도시한 Fig. 6(b)는 결정계수가 0.6 이상으로 나타났고, 회귀직선을 기준으로 왼쪽 상향에 분포한 자료들과 오른쪽 하향에 분포한 자료들을 적절히 구분하고 있는 것으로 판단되었다. 특히, 오른쪽 하향에 분포되어 있는 강우량 300mm 이상이면서 가뭄을 보인 6개의 자료를 살펴보면 4개의 발생자료가 가뭄해인 2001, 2014, 2015, 2017년에 발생을 나타남에 따라 가뭄은 해당월 수분공급 외에 기준월 이전 상태의 지속성도 함께 고려되어야 할 것으로 판단되었다.
산정된 결과를 바탕으로 대상유역의 1월에서 12월까지 각 월별 및 강수량, 하천유량, 댐 유입량에 대한 순위도출 및 순위차를 적용한 회귀분석 상수를 결정하고, 이에 따른 정량화를 수행하였으며, 산정결과는 Table 5로 제시하였다. 여기서 정량화된 값은 정상상태와 가뭄을 구분하는 기준인 MSWSI 가뭄지수 –1에 해당하는 값이다.
월별 수문인자별 정량화된 값의 산정결과 강우와 댐 유입량은 가뭄 기준 값이 8월에 가장 큰 것으로 나타났고, 하천 유입량은 7월이 가장 크게 나타났으며, 월별로는 모든 인자가 9월과 10월 사이에 값의 편차가 크게 변하는 것으로 분석되었다.
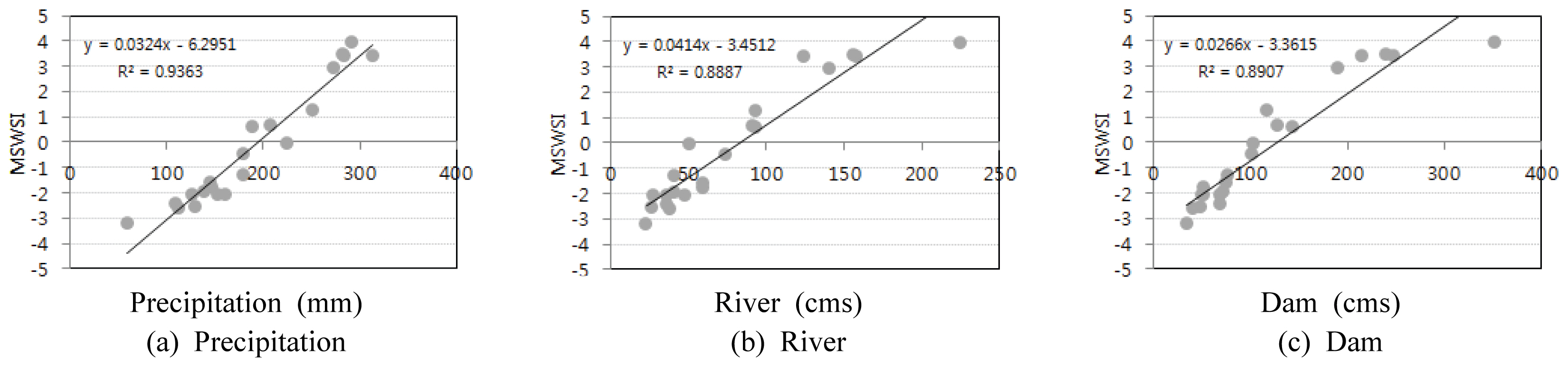
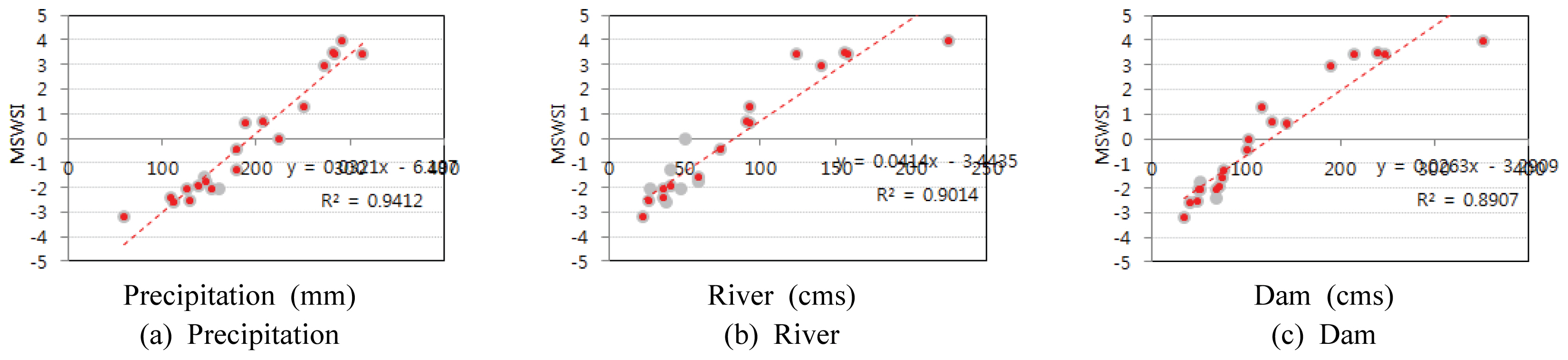
월 단위와 동일한 자료를 이용한 3개월 이동평균에 대한 수문학적 가뭄지수 산정 및 회귀분석을 수행하였다. 월 단위 강수량 자료와 가뭄지수 분석결과에서는 해당되는 월 이전의 습윤상태 반영이 미비함으로 인해 전 자료에 대한 두 인자간의 선형성을 갖지 않는 것으로 나타났으나, 3개월 이동평균을 적용하는 경우에는 기준 월 이전 상태에 대한 반영이 될 수 있다. 월 단위와 달리 3개월 이동평균의 적용은 Fig. 7과 같이 댐 유역 입력인자인 강수량, 하천 유량, 댐 유입량에 대해 각각 도시 및 회귀분석을 수행하였다.
Fig. 7에서와 같이 입력 자료별 가뭄지수의 도시 결과 결정계수가 Fig. 7(a)의 강수량은 0.94, Fig. 7(b)의 하천유량은 0.89, Fig. 7(c)에서는 댐 유출량 0.89로 높은 결정계수를 갖는 것으로 분석되었다.
월 단위 분석과 동일하게 3개월 이동평균에 대한 순위차를 적용하였고, 월 단위 분석과 달리 3개월 이동평균은 전체 자료의 회귀분석 결과가 높은 결정계수를 가짐에 따라 순위차는 15%만 적용하였다. Table 6은 인자별 순위도출 및 순위차의 적용결과이며, 회귀분석을 위한 도시는 Fig. 8로 나타내었다. 순위차 15% 적용에 따른 결정계수는 유사하거나 다소 상향되는 것으로 분석되었다.
인자별 순위차이를 살펴보면 가뭄지수의 순위와 동일순위를 갖는 경우는, 강수량과 하천유량은 각각 3회 및 4회 발생한 반면에 댐 유입량은 11회 발생되었으며, 대부분의 입력인자에서 가뭄지수와의 순위차이가 3 이내에 들어오는 것으로 분석되었다. 가장 큰 순위차이는 4인 경우로 강수량 1회, 하천유량 및 댐 유입량에서 각각 2회의 발생을 보였다.
순위차이가 4가 발생되는 경우는 강수는 가뭄 발생해인 2008년 7월 한 곳에서만 발생되었고, 하천은 2012년과 가뭄 발생해인 2015년에서 발생되었으며, 댐 유역의 경우는 가뭄발생해인 2002년과 연이은 해인 2003년에 발생하였다.
가뭄 구분 기준에 따른 가뭄지수 -1에 해당하는 인자별 정량화 기준값 산출에는 전 자료에 대한 회귀분석을 적용하였으며, 월별 인자별 산정결과는 Table 7로 나타내었다. 산정결과 인자별로 7월에서 10월이 대체적으로 높은 기준 값을 보였고, 이 중에서 9월에 가장 큰 값을 나타낸 반면에 12월에서 3월이 대체적으로 적게 나타났지만 이동평균을 고려하면 10월과 11월은 이전 월의 영향에 따라 다소 높게 산정되었다.
월 단위 및 3개월 이동평균에서 선택된 월별⋅인자별 결정계수를 산정한 결과, 순위차 15%를 적용한 월 단위는 강수량 평균 0.75, 하천유량 0.79, 댐 유입량 0.76으로 나타났고, 전 자료에 대한 3개월 이동평균은 강수량이 0.91, 하천유량 0.88, 댐 유입량 0.91로 분석되었다.
본 연구에서는 월 단위 및 3개월 이동평균에 대한 회귀상수의 결정 및 이를 이용한 정량화된 값을 산정하고자 하였으며, 산정된 결과는 Table 8로 나타내었다.
월 단위 및 3개월 이동평균에 대한 가뭄 판단 기준 값을 산정한 결과 강수의 경우에는 월 단위와 3개월 이동평균 모두 8월이 가장 높게 나타났고, 하천유량은 월 단위와 3개월 이동평균 모두 9월이 가장 높게 나타났으며, 댐 유입량 및 입력 자료의 경우에는 월 단위는 8월, 3개월 이동평균은 9월 기준 값이 가장 크게 분석되었다.
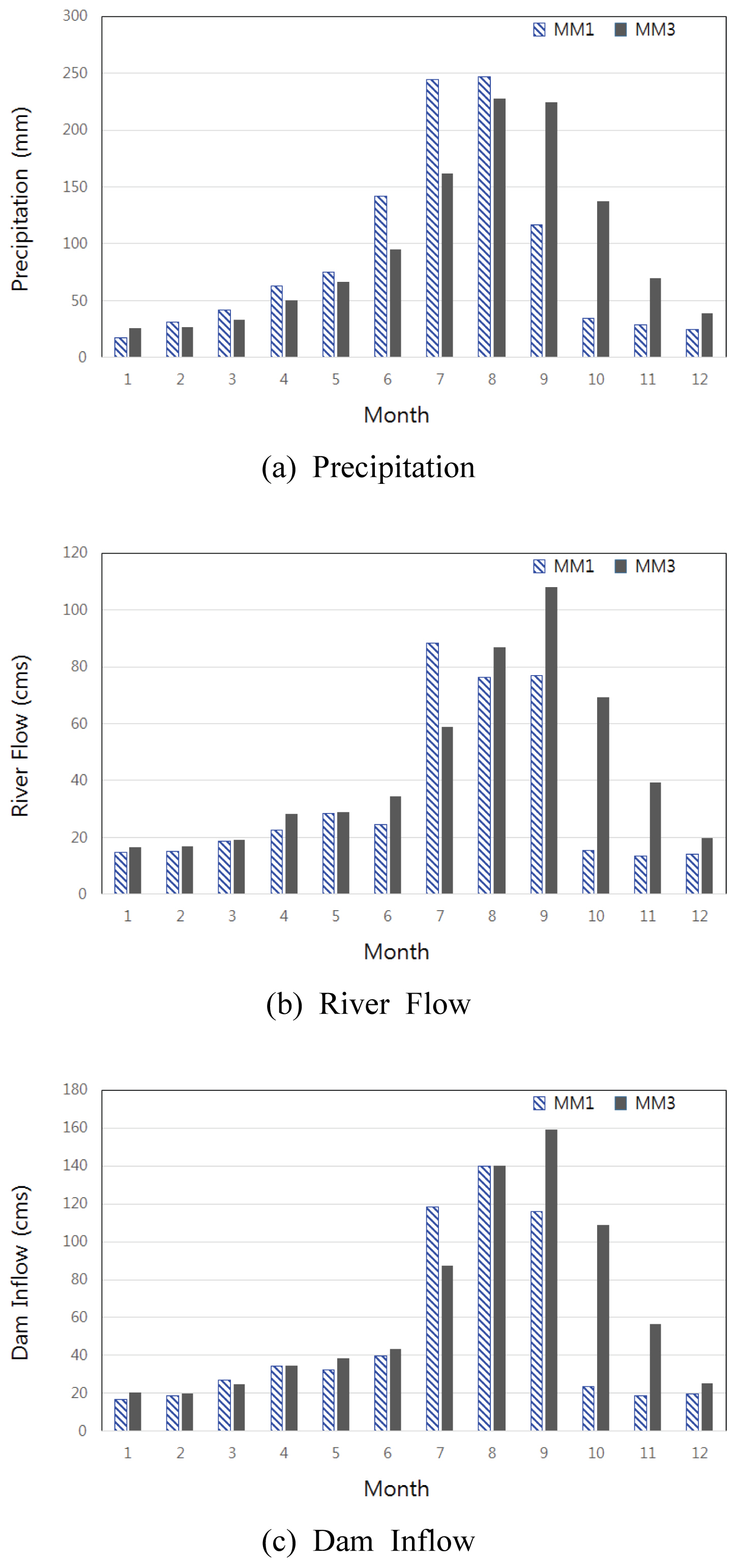
Fig. 9는 입력인자별 Table 8에 산정결과를 월별 및 3개월 이동평균에 대해 막대그래프로 비교 도시하였다. 수문학적 가뭄지수의 여러 입력 인자를 고려함에 따른 가뭄 기준의 정량화 결과 가용수자원에 따른 월별 특징을 적확하게 묘사되는 걸로 판단되었으나 월 단위 및 3개월 이동평균에서는 다소의 차이를 갖는 것으로 판단되었다. 특히 가용수자원 공급량이 높은 3분기와 상대적로 적은 4분기 사이인 10월과 11월에서 큰 차이를 보이는 것으로 분석되었다. 이러한 결과는 3개월 이동평균에서 8월과 9월이 10월 및 11월에 영향관계에 의한 것으로 판단되었으며, 동일한 단위시간을 통한 도시적인 분석을 위해 월 단위 결과를 3개월 단위시간에 맞추어 나타내고자 하였다.
Fig. 10은 월 단위를 3개월 이동평균 시간단위에 맞도록 재산정한 결과와 원래의 3개월 이동평균 결과를 비교 도시하였으며, 그 결과 월별 변화 추세는 유사한 변화를 보이는 반면에 인자별로 월 단위를 3개월로 환산한 결과가 3개월 이동평균에 비해 값이 다소 과소한 추정을 보였다. 강수량의 경우는 최대 값이 차이가 10mm 미만인 반면에 하천유량 및 댐 유입량은 8~9월에서 값이 편차가 강우에 비해 상대적으로 크게 나타났다.
가뭄의 평가를 위해 여러 입력 시계열 자료를 추출하고, 통계적인 개념 및 그에 따른 적절한 분포형의 선택을 통해 가뭄지수를 산정하고, 마련된 범례에 의한 가뭄 심도기준 적용이 이루어지는 것이 일반적이다. 하지만, 이와 같은 가뭄지수에 의한 가뭄평가 방법이 정보전달 측면으로 대상유역에 대한 가뭄평가에는 용이한 반면에 물이용 측면의 활용에는 어려움이 있다. 따라서 본 연구를 통해 가뭄지수와 연관한 입력 인자별 가용수자원의 정량화에 대한 검토를 수행하고자 하였다.
이를 위해 우선적으로 가뭄지수와 입력 인자별 두 인자간의 선형회귀분석 및 회귀상수를 산정하였으며, 그 결과 가뭄 평가를 위한 기준 월 이전 상태를 포함하는 3개월 이동평균에서는 결정계수 0.8 이상의 적정한 회귀식 도출이 가능한 것으로 검토되는 반면에 월 단위에서는 가뭄 이전 습윤상태의 반영이 미비함에 따른 상이한 자료 분포를 보이는 것으로 판단됨에 따라 이를 개선하기 위해 인자별 순위도출 및 가뭄지수와 입력인자간의 순위차에 대한 적용성을 검토하였다.
가뭄 분석을 위한 가용수자원 입력 자료인 강수량, 하천유량, 댐 유입량의 시계열 자료가 대칭적인 자료구조를 갖지는 못하지만 이들 자료의 가중을 고려한 가뭄지수 산정에 있어서는 가뭄지수의 범례가 0을 기준으로 대칭적이고, 통계 분포형의 대칭성으로 판단할 때, 가뭄지수 산정결과 및 결과자료의 상이한 결과 값(수분공급 과잉(부족)에서 가뭄(습윤))이 대칭적인 발생을 보일 수 있다. 본 연구의 대상유역에 대한 월 단위 및 3개월 이동평균에 따른 가뭄지수를 시계열로 도시한 결과, 일부 구간인 2004~2007년에서는 습윤 보다는 가뭄이 두드러진 발생을 보였으나, 가뭄과 습윤의 대칭적인 발생을 보였고, 전체 가뭄지수의 평균값도 음의 방향에서 0에 근접하는 것으로 분석되었다.
또한 본 연구에서는 가뭄지수와 수문인자간의 순위도출 및 순위차를 적용하였으며, 회귀분석을 위한 두 인자에 동일한 특성을 반영하여 순위를 도출한다면 두 인자를 크기 순으로 나열하는 경우 값에 따라 유사한 순위를 가질 것이며, 이에 따른 순위차이도 크지 않은 것으로 예상할 수 있다. 3개월 이동평균에 대한 순위차를 적용한 결과 대부분이 순위차 3 이내의 값을 보였고, 최대 순위차가 4였으며, 이러한 경우는 가뭄해에 발생되는 것으로 분석되었다. 이러한 결과로 미루어 볼 때, 자료 특성이 대칭적인 구조를 갖고, 회귀분석에 따라 높은 결정계수를 보이는 경우 두 인자간의 순위차가 크지 않을 가능성을 갖는 것으로 판단되었다. 이와 달리 월 단위 가뭄분석 결과는 선형적인 자료 분포를 예상하는 경우와 위배되는 방사형 분포를 보였고, 결정계수가 0에 가까우며, 순위 편차도 상당히 높게 나타났다.
단위시간이 다른 두 인자의 결과에 대한 차이는 지속성 있는 물 부족(과잉)에 따른 가뭄(습윤) 발생 특성상 3개월 이동평균이 월 단위보다 기준 월 이전 상태의 정보가 반영된 결과로 이해될 수 있을 것이다.
3개월 이동평균과 달리 월 단위에 대한 순위차이 적용은 편차가 큰 값을 제거하고 일정한 순위 이내의 자료 추출을 통한 회귀분석 수행 및 결과에 대한 검토를 위한 것으로 검토된 순위차 기준은 15%(순위차 3 이내)로 설정하여 적용하였고, 그 결과로 전체 자료 중에서 30% 미만의 자료만이 선별되었으며, 선별된 자료를 이용한 회귀분석 및 회귀직선 도시결과, 결정계수는 0.6 이상이였고, 회귀직선은 상이한 분포를 보이는 자료들을 적절성 있게 구분하는 것으로 분석되었다.
결과적으로 두 가지 단위시간에 따른 회귀상수 도출은 전 기간 자료를 적용한 3개월 이동평균(MM3)과는 달리 월 단위는 순위차 15%를 적용하여 도출하였고, 각각에 대한 각 인자별 정량화된 값을 산정하였으며, 두 인자의 단위시간을 맞추기 위해 월 단위 자료의 결과를 3개월 단위에 맞추어 이동평균(RMM3_M1) 하여 비교검토를 수행하였다.
검토 결과, RMM3_M1가 MM3보다 다소 과소 추정을 보였으나, 패턴 변화에 있어서는 다소 유사성을 갖는 것으로 판단됨에 따라 타당성 있는 정량화가 이루어지는 것으로 판단되었다.
이와 같은 월별 인자별 정량화된 기준 값 산정은 장래 보완 검토의 과정을 통해서 가뭄 대응을 위한 보다 구체적인 값의 제시가 가능할 것으로 판단되며, 특히, 여러 가용수자원 중에서 저장성을 갖는 댐 유입량 운용을 위한 활용방안 등의 마련을 통해 가뭄 대비에 유용성을 가질 것으로 사료되었다.
Fig. 1
Time Series Overlap Plot of Available Water Resources (Precip., River Flow, Dam Inflow) of M1 (monthly) and MM3 (3 months moving average) for St.3006 (July)
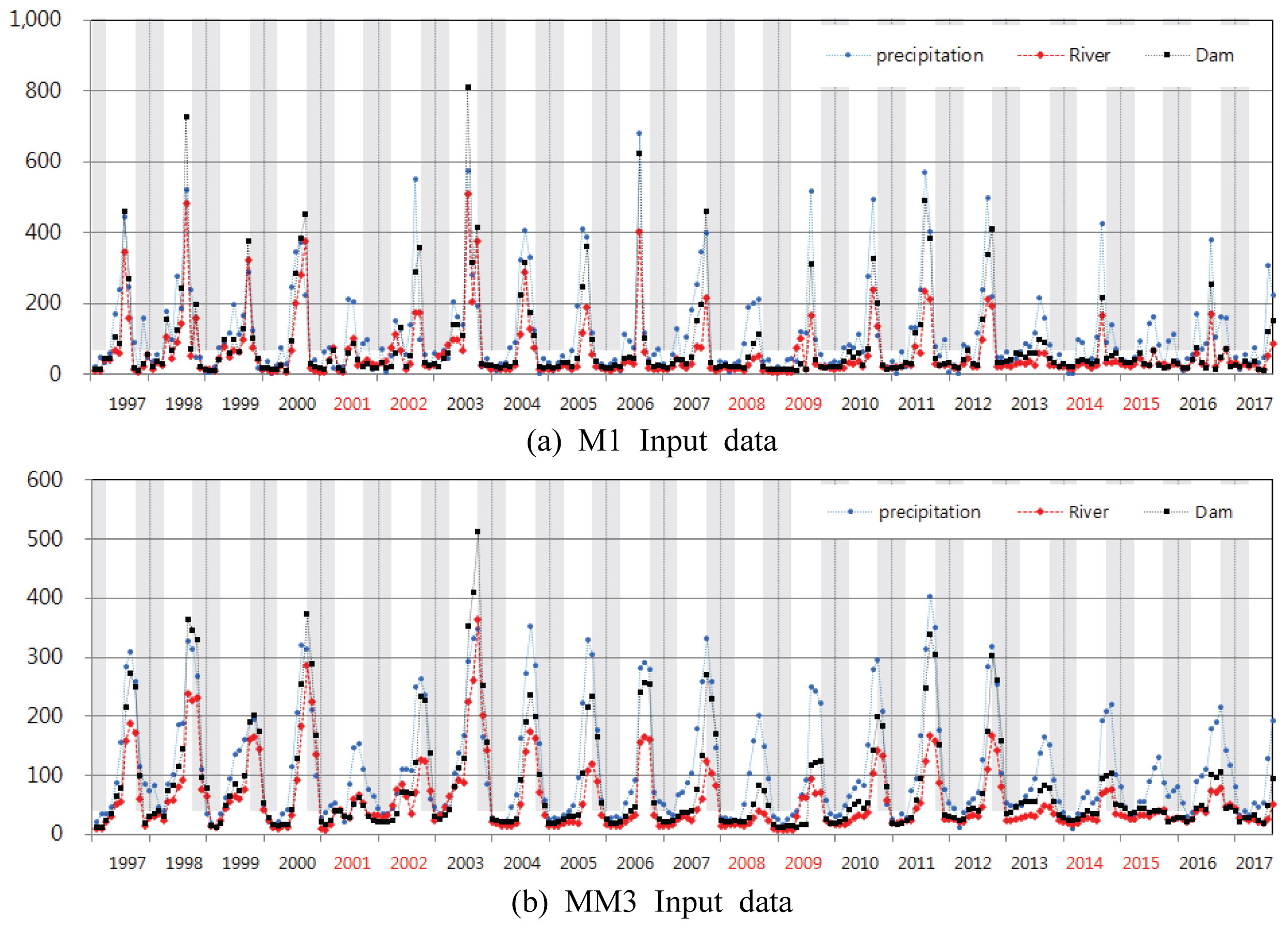
Fig. 10
Bar Graph Comparison of each Input Factor’s Monthly Quantified Value of MM3 & RMM3_M1 (Recalculating 3 months moving average with M1)

Table 1
Characteristic of Station ID.3006
| Station ID | St.3006 | |
|---|---|---|
| MSWSI | Dam type I | |
| Key Station | Precipitation | geumsan |
| River Flow | ogcheon | |
| Dam Inflow | daecheong | |
| Duration (From ~ to) | 1997.01 ~ 2017.08 | |
Table 2
MSWSI Drought Categories
Table 3
M1 MSWSI Result for St.3006 (July)
Table 4
M1 MSWSI Rank Analysis Result for St.3006 (July)
Table 5
Monthly Estimation of M1 Regression Constant & Quantified Value for Drought Index -1
Table 6
MM3 MSWSI Rank Analysis Result for St.3006 (July)
Table 7
Estimation of MM3 Regression Constant & Quantified Value for Drought Index -1
Table 8
Comparison of each Input Factor’s Monthly Quantified Value of M1 & MM3
References
Hollinger, SE, Isard, SA, and Welford, MR (1993). A new soil moisture drought index for predicting crop yields. Proceedings of Preprints, Eighth Conference on Applied Climatology. American Meteorological Society, Anaheim, CA: p 187-190.

IPCC (2007). Climate Change 2007: The physical science basis. Contribution of working group I to the fourth assessment report of the intergovernmental panle on climate change. Cambridge University Press, Cambridge, UK.

Jang, SH, Lee, JK, Oh, JH, and Jo, JW (2016) The probabilistic drought forecast based on ensemble using improvement of the modified surface water supply index. J Korea water Resour Assoc, Vol. 49, No. 10, pp. 835-849.

Jeong, MS, Kim, JS, Jang, HW, and Lee, JH (2016) ROC evaluation for MLP ANN drought forecasting model. J Korea water Resour Assoc, Vol. 49, No. 10, pp. 877-885.

Jeong, MS, Lee, CH, Lee, JH, and Hong, IP (2017) Analysis of hydrological drought considering MSWSI and precipitation. Journal of the Korea Academia-Industrial cooperation Society, Vol. 18, No. 12, pp. 668-678.

Kwon, HJ, and Kim, SJ (2007) Methodology of drought assessment using national groundwater monitoring network data. Journal of the Korean Society of Civil Engineers, Vol. 27, No. 2B, pp. 193-199.

Kwon, HJ, Park, HJ, Hong, DO, and Kim, SJ (2006) A study on semi-distributed hydrologic assessment modifying SWSI. J Korea Water Resour Assoc, Vol. 39, No. 8, pp. 645-658.

Lee, BR, Sung, JH, and Chung, ES (2015) Comparison of meteorological drought and hydrological index. J Korea water Resour Assoc, Vol. 48, No. 1, pp. 69-78.

Lee, DR, Lee, DH, and Kang, SU (2003) Drought triggers and monitoring system. J Korea water Resour Assoc, Vol. 36, No. 3, pp. 375-384.

Lee, JH, Kim, JS, Jang, HW, and Lee, JC (2013) Drought forecasting using the multi layer perceptron (MLP) artificial neural network model. J Korea water Resour Assoc, Vol. 46, No. 12, pp. 1249-1263.

Palmer, WC (1965). Meteorological drought. Weather Bureau Research Paper No. 45. U.S. Department of Commerce, Washington, D.C: p 1-58.

Shafer, B, and Dezman, L (1982) Development of a surface water supply index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. Proceedings of the 50th Annual Western Snow Conference, pp. 164-175.

Stahl, K (2001). Hydrological drought: A study across Europe. PhD dissertation. Freiburg University; Germany.

- TOOLS
-
METRICS

-
- 1 Crossref
- 2,949 View
- 66 Download