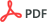|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(5); 2018 > Article |
|
Abstract
There have been many limitations in the application of the hydrological field in Korea due to doubts about its accuracy, although radar-estimated rainfall has the advantage of providing high temporal and spatial resolution data. Real time ZR parameter calculation methods and many quantitative correction methods using rain gauge rainfall have been introduced to overcome the problem of accuracy. However, the accuracy of the radar rainfall after correction by these methods was a little better than before because the radar rainfall converted by the radar reflectivity had serious errors. In this study, we quantified the errors inherent in the radar reflectivity to solve the problem of accuracy of radar rainfall which has been raised in Korea over the last 10 years. The results
are as follows. In the case assuming that the error variance of the radar reflectivity was 0, the bias of radar reflectivity ranged from ŌĆō1 dBZ to ŌĆō14 dBZ. In the case considering error variance, the bias of the radar reflectivity ranged from ŌĆō3 dBZ to ŌĆō15 dBZ, and the error variance ranged from 22 to 82 dBZ2.
ņÜöņ¦Ć
ļĀłņØ┤ļŹö Ļ░ĢņÜ░ ņ×ÉļŻīļŖö ņŗ£Ļ│ĄĻ░äņĀüņ£╝ļĪ£ ļåÆņØĆ ĒĢ┤ņāüļÅä ņ×ÉļŻīļź╝ ņĀ£Ļ│ĄĒĢ£ļŗżļŖö ņןņĀÉņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ĻĘĖ ņĀĢĒÖĢļÅäņŚÉ ļīĆĒĢ£ ņØśĻĄ¼ņŗ¼ņ£╝ļĪ£ ĻĄŁļé┤ ņłśļ¼ĖļČäņĢ╝ ņĀüņÜ®ņŚÉ ļ¦ÄņØĆ ĒĢ£Ļ│äĻ░Ć ņ׳ņ¢┤ ņÖöļŗż. ņØ┤ņÖĆ Ļ░ÖņØĆ ņĀĢĒÖĢļÅäņØś ļ¼ĖņĀ£ņĀÉņØä ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢ┤ ņŗżņŗ£Ļ░ä ZR ļ¦żĻ░£ļ│Ćņłś ņé░ņĀĢ ļ░®ļ▓Ģ ļ░Å ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ļź╝ ņØ┤ņÜ®ĒĢ£ ņĀĢļ¤ēņĀü ļ│┤ņĀĢ ļ░®ļ▓ĢņØ┤ ļÅäņ×ģļÉśņ¢┤ ņÖöļŗż. ĻĘĖļ¤¼ļéś ņØ┤ļ»Ė ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ņśżņ░©Ļ░Ć Ēü¼Ļ▓ī ļé┤ņ×¼ļÉ£ ņāüĒÖ®ņŚÉņä£ ļ│ĆĒÖśļÉ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ĻĘĖ ņ¢┤ļ¢ĀĒĢ£ ļ░®ļ▓Ģņ£╝ļĪ£ ļ│┤ņĀĢļÉśņ¢┤ļÅä ņŚ¼ņĀäĒ׳ ļ¦ÄņØĆ ļ¼ĖņĀ£ņĀÉņØ┤ ņ׳ņØä ņłśļ░¢ņŚÉ ņŚåņŚłļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦Ćļé£ 10ļģä ļÅÖņĢł ĻĄŁļé┤ņŚÉņä£ ņĀ£ĻĖ░ļÉśņ¢┤ ņś© ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ņĀĢĒÖĢļÅä ļ¼ĖņĀ£ņĀÉņŚÉ ļīĆĒĢ£ ĒĢ┤Ļ▓░ņ▒ģņØä ņĀ£ņŗ£ĒĢśĻĖ░ ņ£äĒĢ┤ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ļé┤ņ×¼ļÉśņ¢┤ ņ׳ļŖö ņśżņ░©ļź╝ ņĀĢļ¤ēĒÖö ĒĢśņśĆļŗż. ĻĘĖ Ļ▓░Ļ│╝ļŖö ļŗżņØīĻ│╝ Ļ░Öļŗż. ļ©╝ņĀĆ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņśżņ░©ļČäņé░ņØä 0ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢ£ Ļ▓ĮņÜ░ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö ŌĆō1 dBZņŚÉņä£ ŌĆō14 dBZļĪ£ ļéśĒāĆļé¼ļŗż. ĻĘĖļ¤¼ļéś ņśżņ░©ļČäņé░ņØä Ļ│ĀļĀżĒĢ£ Ļ▓ĮņÜ░ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö ŌĆō3 dBZņŚÉņä£ ŌĆō15 dBZĻ╣īņ¦Ć ļéśĒāĆļé¼ņ£╝ļ®░, ĻĘĖ ņśżņ░©ļČäņé░ņØĆ 22Ōł╝82 dBZ2 ņé¼ņØ┤ņØś ļ▓öņ£äļĪ£ ļéśĒāĆļé¼ļŗż.
ļīĆĻĖ░ņłśņāüņ▓┤ņŚÉ ļīĆĒĢ£ ĻĖ░ņāüļĀłņØ┤ļŹöņØś Ļ┤ĆņĖĪ Ļ│╝ņĀĢņŚÉņä£ļŖö ļ¦ÄņØĆ ņĀĢļ│┤ļōżņØ┤ ņåÉņŗżļÉśĻ│Ā ņśłņĖĪ Ļ░ĆļŖźĒĢśĻ▒░ļéś ļČłĻ░ĆļŖźĒĢ£ ņśżņ░©Ļ░Ć ļ░£ņāØĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ļĀłņØ┤ļŹö Ļ┤ĆņĖĪ ņ×ÉļŻīņŚÉļŖö ļŗżņ¢æĒĢ£ ņśżņ░©ļōżņØ┤ ļéśĒāĆļéśĻ│Ā ņ׳ļŗż(Krajewski and Smith, 2002). ĻĘĖļ”¼Ļ│Ā ņØ┤ļ¤¼ĒĢ£ ņśżņ░©ļōżņØĆ ĻĖ░ņāüļĀłņØ┤ļŹöņÖĆ Ļ┤ĆļĀ©ĒĢ£ ļŗżņ¢æĒĢ£ ļČäņĢ╝ņØś ņĀäļ¼ĖĻ░ĆļōżņŚÉ ļö░ļØ╝ ļŗżņ¢æĒĢ£ ņŗ£Ļ░üņ£╝ļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ļŗż. ņĀäņ×É ļ░Å ĒåĄņŗĀ ļČäņĢ╝ņŚÉņä£ļŖö ņŻ╝ļĪ£ ļĀłņØ┤ļŹö ĒĢśļō£ņø©ņ¢┤ Ļ▓Ćļ│┤ņĀĢņŚÉņä£ ļéśĒāĆļéśļŖö ņśżņ░©ļéś ņŗĀĒśĖņ▓śļ”¼ Ļ│╝ņĀĢņŚÉņä£ņØś ņśżņ░©ļź╝ ņŻ╝ņÜö ņśżņ░©ļōżļĪ£ ļ░öļØ╝ļ│┤Ļ│Ā ņ׳ļŗż(Atlas, 2002). ņØ┤ņŚÉ ļ╣äĒĢ┤ ĻĖ░ņāü ļČäņĢ╝ņŚÉņä£ļŖö ĒśĖņÜ░ņØś ņóģļźśņŚÉ ļö░ļźĖ Ļ░ĢņÜ░ Ēü¼ĻĖ░ ņ×ģņ×ÉļČäĒżņØś ļ│ĆļÅÖņä▒Ļ│╝ ļĀłņØ┤ļŹö Ļ░Ģņłś ņČöņĀĢ ņĢīĻ│Āļ”¼ņ”śņØś ļ¦żĻ░£ļ│Ćņłś ļō▒ņØä ņŻ╝ņÜö ņśżņ░© ņøÉņØĖņ£╝ļĪ£ ļ░öļØ╝ļ│┤Ļ│Ā ņ׳ļŗż(Gosset et al., 2010). ņØ┤ļ¤¼ĒĢ£ ņĀäņ×É, ĒåĄņŗĀ, ĻĖ░ņāü ļČäņĢ╝ņŚÉņä£ņØś ņśżņ░© ņøÉņØĖņØä ĒīīņĢģĒĢśĻ│Ā ņĀ£Ļ▒░ĒĢśņśĆļŗż ĒĢĀņ¦ĆļØ╝ļÅä ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļź╝ ņłśļ¼ĖļČäņäØņŚÉ ĒÖ£ņÜ®ĒĢśļŖö ņłśļ¼Ė ņĀäļ¼ĖĻ░ĆļōżņŚÉĻ▓īļŖö ņŚ¼ņĀäĒ׳ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņŚÉ ņśżņ░©Ļ░Ć ņĪ┤ņ×¼ĒĢ£ļŗżļŖö ļ¼ĖņĀ£ņĀÉņØä ņĀ£ĻĖ░ĒĢśņŚ¼ ņÖöļŗż(Seo and Krajewski, 2011; Yoon, Choi, et al., 2016; Yoon et al., 2017).
ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņŚÉ ņśżņ░©Ļ░Ć ņĪ┤ņ×¼ĒĢ£ļŗżļŖö ļ¼ĖņĀ£ņĀÉņØĆ ĻĄŁļé┤ņŚÉ 2006ļģäļČĆĒä░ ļÅäņ×ģļÉśņŚłļŹś ĻĖ░ņāüļĀłņØ┤ļŹö(Sļ░┤ļō£ ļŗ©ņØ╝ĒÄĖĒīīļĀłņØ┤ļŹö)ņŚÉņä£ļÅä ļ¦łņ░¼Ļ░Ćņ¦ĆļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ņŚłļŗż. ĒŖ╣Ē׳ ĻĄŁļé┤ ĻĖ░ņāüļĀłņØ┤ļŹöļŖö ĻĘĖ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ĒÄĖņØśĻ░Ć ņŗ¼Ļ░üĒĢśĻ▓ī ļéśĒāĆļéś ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņŚÉ ļ╣äĒĢ┤ ņĀĢļ¤ēņĀüņ£╝ļĪ£ 30% ņłśņżĆņŚÉ ļČłĻ│╝ĒĢśņśĆļŗż(Yoo et al., 2013; Yoon, Choi, et al., 2016). ņØ┤ļ¤¼ĒĢ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś Ļ│╝ņåīĒĢ£ ļ¼ĖņĀ£ņĀÉņØä ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ┤ ĻĄŁļé┤ ĻĖ░ņāüĒĢÖņ×ÉļōżņØĆ ZR Ļ┤ĆĻ│äņŗØ(R=AZb)ņØś ļ¦żĻ░£ļ│Ćņłś(AņÖĆ b)ļź╝ ņŗżņŗ£Ļ░äņ£╝ļĪ£ ņČöņĀĢĒĢśļŖö ļ░®ļ▓ĢļōżņØä ņĀüņÜ®ĒĢśņŚ¼ ņÖöļŗż(MRI, 2004; Suk et al., 2005; Kim and Yoo, 2014). ņØ┤ņŚÉ ļ╣äĒĢ┤ ņ¦ĆņāüņŚÉ ļ¢©ņ¢┤ņ¦ä Ļ░ĢņÜ░ņØś ņ¢æņØä ņżæņÜöņŗ£ĒĢśĻ▓ī ņŚ¼Ļ▓╝ļŹś ĻĄŁļé┤ ņłśļ¼ĖĒĢÖņ×ÉļōżņØĆ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļź╝ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņÖĆ ļ╣äņŖĘĒĢśĻ▓ī ļ¦×ņČöļŖö ĒåĄĻ│äņĀü ļ░®ļ▓ĢļōżņØä ņĀüņÜ®ĒĢśņśĆļŗż. G/R ļ╣äļź╝ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņŚÉ Ļ│▒ĒĢśļŖö ļ░®ļ▓Ģ(Yoo et al., 2013), Co-Kriging (Krajewski, 1987; Seo et al., 1990) ļ░Å SCM (Kim et al., 2008) ļō▒ņØ┤ ļīĆĒæ£ņĀüņØĖ ņśłņØ┤ļŗż.
ņłśļ¼Ė ņĀäļ¼ĖĻ░ĆļōżņØ┤ ņŻ╝ļĪ£ ņé¼ņÜ®ĒĢśņŚ¼ ņÖöļŹś ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļź╝ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņÖĆ ņ£Āņé¼ĒĢśĻ▓ī ļ¦īļō£ļŖö ĒåĄĻ│äņĀüņØĖ ĻĖ░ļ▓ĢļōżņØĆ ĻĘĖļ¤¼ļéś ļŗżņØīĻ│╝ Ļ░ÖņØĆ ļ¼ĖņĀ£ņĀÉņØ┤ ņĪ┤ņ×¼ĒĢ£ļŗż. ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ļĀłņØ┤ļŹö ĒÄĖĒīīļ│Ćņłśļź╝ ļ╣äņäĀĒśĢ Ļ┤ĆĻ│äņŗØ, ņśłļź╝ ļōżņ¢┤ ZR Ļ┤ĆĻ│äņŗØņŚÉ ņ×ģļĀźĒĢśņŚ¼ ņČöņĀĢļÉśļŖö Ļ▓āņØ┤ĻĖ░ņŚÉ ļĀłņØ┤ļŹö ĒÄĖĒīīļ│ĆņłśņŚÉ ņśżņ░©Ļ░Ć ļé┤ņ×¼ļÉśņ¢┤ ņ׳ļŗżļ®┤ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņŚÉ ļ╣äņäĀĒśĢņĀüņ£╝ļĪ£ ņĀäĒīīļÉśĻ│Ā ņØ┤ļ¤¼ĒĢ£ ļ╣äņäĀĒśĢņĀüņ£╝ļĪ£ ņĀäĒīīļÉ£ ņśżņ░©ļź╝ ļé┤ņ×¼ĒĢ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļź╝ ĒåĄĻ│äņĀüņØĖ ĻĖ░ļ▓Ģņ£╝ļĪ£ ļ│┤ņĀĢĒĢśĻ▓ī ļÉśļ®┤ ĻĘĖ ņśżņ░©ļŖö ļŹöņÜ▒ ņ”ØĒÅŁļÉĀ Ļ░ĆļŖźņä▒ņØ┤ Ēü¼ļŗż. ņØ╝ļĪĆļĪ£ ĻĄŁļé┤ņŚÉņä£ ņēĮĻ▓ī ņĀüņÜ®ļÉśņ¢┤ ņÖöļŹś G/R ļ╣äļź╝ ļĀłņØ┤ļŹöĻ░ĢņÜ░ņŚÉ Ļ│▒ĒĢśļŖö ļ░®ļ▓ĢņØĆ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļź╝ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņÖĆ ņ£Āņé¼ĒĢśĻ▓ī ļ¦īļōż ņłśļŖö ņ׳ņ£╝ļéś ņśżņ░©ņØś ļ│ĆļÅÖņä▒ņØä ļåÆņØ┤Ļ│Ā ņāüĻ┤Ćņä▒ņØä Ļ░Éņåīņŗ£ĒéżļŖö ļ░®ļ▓ĢņØ┤ņŚłļŗż(Yoo et al., 2013; Yoo et al., 2016; Yoon, Choi, et al., 2016).
ĻĄŁļé┤ ĻĖ░ņāü ļ░Å ņłśļ¼ĖĒĢÖņ×ÉļōżņØĆ Sļ░┤ļō£ ņØ┤ņżæĒÄĖĒīīļĀłņØ┤ļŹöĻ░Ć ļÅäņ×ģļÉśļ®┤ ņØ┤ļ¤¼ĒĢ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ĒÄĖņØśĻ░Ć ņĀ£Ļ▒░ ļÉĀ Ļ▓āņØ┤ļØ╝ ņāØĻ░üĒĢśņśĆļŗż. ņØ┤ņŚÉ ĻĄŁĒåĀĻĄÉĒåĄļČĆ ĒĢ£Ļ░ĢĒÖŹņłśĒåĄņĀ£ņåīņŚÉņä£ ļÅäņ×ģļÉ£ ļ╣äņŖ¼ņé░ļĀłņØ┤ļŹöĻ░Ć ņĄ£ņ┤łņØś Sļ░┤ļō£ ņØ┤ņżæĒÄĖĒīīļĀłņØ┤ļŹöļĪ£ 2009ļģäņŚÉ ļÅäņ×ģļÉ£ ņØ┤Ēøä ņØ┤ņżæĒÄĖĒīīļĀłņØ┤ļŹöĻ░Ć ļÅäņ×ģļÉśĻ▓ī ļÉ£ļŗż. ĻĘĖļ¤¼ļéś S-ļ░┤ļō£ ņØ┤ņżæĒÄĖĒīīļĀłņØ┤ļŹöņŚÉņä£ ņĀ£Ļ│ĄļÉśļŖö ĒÄĖĒīīļ│ĆņłśļĪ£ ņČöņĀĢļÉ£ ļĀłņØ┤ļŹöĻ░ĢņÜ░ņØś ņĀĢĒÖĢļÅäļŖö ĒÄĖĒīīļ│ĆņłśņŚÉ ļīĆĒĢ£ ņĪ░ņĀł ņŚåņØ┤ļŖö ļŗ©ņØ╝ĒÄĖĒīīļĀłņØ┤ļŹöņÖĆ ļ╣äņŖĘĒĢ£ ņłśņżĆņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż(Yoon, Suk, et al., 2016). ņØ┤ņŚÉ Yoon, Suk, et al. (2016)ņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö WRC (2015)ņŚÉņä£ Ļ░£ļ░£ĒĢ£ Z-ZDR Ļ┤ĆĻ│äņÖĆ Z-KDP Ļ┤ĆĻ│äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Z, ZDR, KDPļź╝ ļÅÖņŗ£ņŚÉ ņĪ░ņĀłĒĢśņŚ¼ ļĀłņØ┤ļŹöĻ░Ģņłśļ¤ēņØś ĒÆłņ¦łņØä Ē¢źņāüņŗ£ņ╝░ļŗż. ĻĘĖ Ļ▓░Ļ│╝ 70% ņØ┤ņāüņØś ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ņĀĢĒÖĢļÅä(1-NE)ļź╝ ĒÖĢļ│┤ĒĢśņśĆļŗż.
Yoon, Suk, et al. (2016) ņŚ░ĻĄ¼ņŚÉņä£ ņŻ╝ļ¬®ĒĢĀ Ļ▓āņØĆ ļ░śņé¼ļÅäņØś ĒÄĖņØśļź╝ ņĀ£Ļ▒░ĒĢ┤ņĢ╝ 70% ņØ┤ņāüņØś ņĀĢĒÖĢļÅäļź╝ ĒÖĢļ│┤ĒĢĀ ņłś ņ׳ļŗżļŖö ņĀÉņØ┤ņŚłļŗż. ņŗ¼ņ¦Ćņ¢┤ ļ░śņé¼ļÅäļ¦īņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņČöņĀĢļÉ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ ņŚŁņŗ£ļÅä ļ░śņé¼ļÅäņØś ĒÄĖņØśļź╝ ņĀ£Ļ▒░ĒĢ┤ņŻ╝ļ®┤ 70% ņØ┤ņāüņØś ņĀĢĒÖĢļÅäļź╝ ĒÖĢļ│┤ĒĢĀ ņłś ņ׳ņŚłļŗż. ņØ┤ļŖö ĻĄŁļé┤ ļĀłņØ┤ļŹöņŚÉņä£ ņĀ£Ļ│ĄļÉśĻ│Ā ņ׳ļŖö ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ļ¦żņÜ░ Ēü░ ņśżņ░©Ļ░Ć ļé┤ņ×¼ļÉśņ¢┤ ņ׳ņØīņØä ņØśļ»ĖĒĢ£ļŗż. ņ”ē, ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ĒÄĖņØśļŖö ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņśżņ░©ņŚÉ ĻĖ░ņØĖĒĢ┤ ņÖöņŚłļŹś Ļ▓āņØ┤ļŗż. ņé¼ņŗż ĻĄŁļé┤ ĻĖ░ņāüļĀłņØ┤ļŹöļĪ£ļČĆĒä░ ņĀ£Ļ│ĄļÉśņ¢┤ ņśżļŹś ļĀłņØ┤ļŹö ļ░śņé¼ļÅä ņśżņ░©ļŖö Park and Lee (2010)ņŚÉņä£ ņĄ£ņ┤łļĪ£ ņĀ£ņŗ£ĒĢśņśĆļŗż. Park and Lee (2010)ļŖö ņ¦ĆņāüņØś Ļ┤ĆņĖĪ ĻĖ░ĻĖ░ļĪ£ļČĆĒä░ ņČöņĀĢļÉ£ DSDļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĒĢ£ ĻĖ░ņāüļĀłņØ┤ļŹöļź╝ ļ│┤ņĀĢĒĢśĻ│Ā ĻĘĖ ļ│┤ņĀĢļÉ£ ĻĖ░ņāüļĀłņØ┤ļŹöļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņĀäĻĄŁ ĻĖ░ņāüļĀłņØ┤ļŹöņØś ļ░śņé¼ļÅä ļ│┤ņĀĢĻ░ÆņØä ņĀ£ņŗ£ĒĢ£ļ░ö ņ׳ļŗż. ĻĘĖ Ļ▓░Ļ│╝ ņĀäĻĄŁ ĻĖ░ņāüļĀłņØ┤ļŹöņØś ļ░śņé¼ļÅäļŖö ņ×æĻ▓īļŖö -3 dBZņŚÉņä£ Ēü¼Ļ▓īļŖö -12 dBZ ņĀĢļÅäņØś ņśżņ░©Ļ░Ć ļ░£ņāØĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļ░ØĒśĆņĪīļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦Ćļé£ 10ļģä ļÅÖņĢł ĻĄŁļé┤ņŚÉņä£ ņĀ£ĻĖ░ļÉśņ¢┤ ņś© ļĀłņØ┤ļŹö Ļ░ĢņÜ░ ņČöņĀĢļ¤ēņØś Ļ│╝ņåīĒĢ£ ļ¼ĖņĀ£ņĀÉņŚÉ ļīĆĒĢ£ ĒĢ┤Ļ▓░ņ▒ģņØä ņĀ£ņŗ£ĒĢśĻĖ░ ņ£äĒĢ┤ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ļé┤ņ×¼ļÉśņ¢┤ ņ׳ļŖö ņśżņ░©ļź╝ ņĀĢļ¤ēĒÖöĒĢśņśĆļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ Yoon (2013)ņŚÉņä£ ņØ┤ļĪĀņĀüņ£╝ļĪ£ ņ£ĀļÅäļÉ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅä ĒÄĖņØś ņŗØĻ│╝ Yoon, Suk, et al. (2016)ņØś Ļ▓ĮĒŚśņĀü ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņśżņ░©ļź╝ ņČöņĀĢĒĢśņśĆļŗż.
ļĀłņØ┤ļŹö ļ░śņé¼ļÅä ņ×ÉļŻī ņé░ņČ£ Ļ│╝ņĀĢņŚÉļŖö ļŗżņ¢æĒĢ£ ņśżņ░©Ļ░Ć ĒżĒĢ©ļÉĀ ņłś ņ׳ņ£╝ļ®░, ņØ┤ļ¤¼ĒĢ£ ņśżņ░©ļŖö ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņŚÉ ņ¦üņĀæņĀüņØĖ ņśüĒ¢źņØä ļ»Ėņ╣Ā ņłś ņ׳ļŗż. ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņśżņ░©ļŖö ļ│┤ĒåĄ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņĀĢņØśļÉĀ ņłś ņ׳ļŗż(Koistinen et al., 2004).
ņŚ¼ĻĖ░ņä£, Ōłł(X, h)ļŖö Ļ▒░ļ”¼ rĻ│╝ ļ░®ņ£äĻ░ü ╬ĖļĪ£ ņĀĢņØśļÉśļŖö ņ£äņ╣ś XņÖĆ Ļ│ĀļÅä hņŚÉņä£ņØś ņśżņ░©ļź╝ ņØśļ»ĖĒĢśĻ│Ā ļŗ©ņ£äļŖö dBZņØ┤ļŗż. Z(X, h)ņÖĆ z(X, h)ļŖö (X, h) ņ¦ĆņĀÉņŚÉņä£ņØś ļ░śņé¼ļÅäļź╝ ņØśļ»ĖĒĢśļ®░ Ļ░üĻ░ü mm6/m3Ļ│╝ dBZņØś ļŗ©ņ£äļź╝ Ļ░¢ļŖöļŗż. ZT(X, h)ņÖĆ zT(X, h)ļŖö ņ░ĖĻ░ÆņØś ļ░śņé¼ļÅäļź╝ ļéśĒāĆļéĖļŗż.
ļ░śņé¼ļÅä zņØś ĒÅēĻĘĀņØĆ Eq. (1)ļĪ£ļČĆĒä░ ņ░ĖĻ░ÆņØś ļ░śņé¼ļÅä zTņØś ĒÅēĻĘĀĻ│╝ ņśżņ░© ŌłłņØś ĒÅēĻĘĀņØś ĒĢ®ņ£╝ļĪ£ ņĀĢņØśļÉĀ ņłś ņ׳ļŗż. zTļŖö ņ░ĖĻ░ÆņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ĻĘĖ ņ×Éņ▓┤Ļ░Ć ĒÅēĻĘĀņØś Ļ░ÆĻ│╝ Ļ░Öņ£╝ļ®░ ņśżņ░© ŌłłņØś ĒÅēĻĘĀņØĆ ĒÄĖņØś ╬╝zļĪ£ ņĀĢņØśĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ļ░śņé¼ļÅä zņØś ĒÅēĻĘĀņØĆ zT+╬╝zĻ░Ć ļÉ£ļŗż. ļ░śņé¼ļÅä zņØś ļČäņé░ ņŚŁņŗ£ļÅä ņ░ĖĻ░ÆņØś ļ░śņé¼ļÅä zTņØś ļČäņé░Ļ│╝ ņśżņ░© ŌłłņØś ļČäņé░ņØś ĒĢ®ņ£╝ļĪ£ ņĀĢņØś ļÉĀ ņłś ņ׳ļŗż. ļ¼╝ļĪĀ ņ░ĖĻ░ÆņØś ļ░śņé¼ļÅä zTņØś ļČäņé░ņØĆ 0ņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ļ░śņé¼ļÅä zņØś ļČäņé░ņØĆ Ļ▓░ĻĄŁ ņśżņ░© ŌłłņØś ļČäņé░Ļ│╝ Ļ░Öļŗż. ņśżņ░© ŌłłņØś ļČäņé░ņØĆ Žā z 2 Žā z 2
Yoon (2013)ņŚÉņä£ļŖö ņĀĢĻĘ£ļČäĒżļź╝ ļö░ļź┤ļŖö Ļ▓āņ£╝ļĪ£ Ļ░ĆņĀĢļÉ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ĒÄĖņØś ╬╝zņÖĆ ņśżņ░©ļČäņé░ Žā z 2
ļśÉĒĢ£ Yoon (2013)ņŚÉņä£ļŖö ļ╣äņ£©(ratio)ļĪ£ Ēæ£ĒśäļÉśļŖö ļĀłņØ┤ļŹö Ļ░ĢņÜ░ RņØś ĒÄĖņØśļź╝ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņ£ĀļÅäĒĢśņśĆļŗż.
Yoon, Suk, et al. (2016)ņŚÉņä£ ņĀ£ņŗ£ĒĢ£ Ļ▓ĮĒŚśņĀü ļ░®ļ▓ĢņØĆ WRC (2015)ņŚÉņä£ ņĀ£ņŗ£ĒĢ£ Z-ZDR ļ░Å Z-KDP Ļ┤ĆĻ│äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļĀłņØ┤ļŹö ļ│Ćņłśļź╝ ņĪ░ņĀł Ēøä ļĀłņØ┤ļŹö Ļ░Ģņłśļ¤ēņØś ņĀĢĒÖĢļÅäļź╝ Ē¢źņāüņŗ£Ēé© ļ░®ļ▓ĢņØ┤ļŗż. ļ│Ė ļ░®ļ▓ĢņØś Ļ│╝ņĀĢņØĆ ļŗżņØīĻ│╝ Ļ░Öļŗż. ļ©╝ņĀĆ, ņÜ░ļ¤ēĻ│ä ņ¦ĆņĀÉĻ│╝ ļÅÖņØ╝ĒĢ£ ļĀłņØ┤ļŹö ņ¦ĆņĀÉņŚÉņä£ņØś ĒśĖņÜ░ņé¼ļĪĆ ņĀäņ▓┤ ņŗ£Ļ░äņŚÉ ļīĆĒĢ£ Z-ZDRņØś ņØ┤ļ│Ćļ¤ē ļČäĒżņÖĆ Z-KDPņØś ņØ┤ļ│Ćļ¤ē ļČäĒżļź╝ ņČöņČ£ĒĢ£ļŗż. ĻĘĖļ”¼Ļ│Ā ĻĘĖ ņØ┤ļ│Ćļ¤ē ļČäĒżņØś ņĄ£ļ╣łĻ░ÆņØ┤ ņØ┤ņżæĒÄĖĒīīļ│Ćņłś Ļ┤ĆĻ│ä ņ£äņŚÉ ņ׳ļÅäļĪØ ĒĢ£ļŗż. ĻĘĖļ¤¼ļéś ļ¼ĖņĀ£ļŖö ņĄ£ļ╣łĻ░ÆņØ┤ ņØ┤ņżæĒÄĖĒÄ┤ļ│ĆņłśņØś ņ¢┤ļŖÉ Ļ││ņŚÉ ņ£äņ╣śĒĢ┤ ņ׳ļŖÉļāÉ ņØ┤ļŗż. ņØ┤ņŚÉ 0ņŚÉņä£ 10ļō▒ĻĖēĻ╣īņ¦Ć ļ░śņé¼ļÅäļź╝ 0 dBZņŚÉņä£ 10 dBZĻ╣īņ¦Ć 1 dBZ Ļ░äĻ▓®ņ£╝ļĪ£ Ļ░Ćņé░ĒĢśņŚ¼ ņØ┤ļĢī ņØ┤ļ│Ćļ¤ē ļČäĒżņØś ņĄ£ļ╣łĻ░ÆņØ┤ ņØ┤ņżæĒÄĖĒīīļ│Ćņłś Ļ┤ĆĻ│ä ņ£äņŚÉ ņ׳ļÅäļĪØ ZDRĻ│╝ KDPļź╝ ņ”ØĻ░ÉĒĢ£ļŗż.
Ļ░ü ļō▒ĻĖēņŚÉ ļö░ļźĖ Z, ZDR, KDPļź╝ ņé░ņĀĢĒĢśņŚ¼ ļĀłņØ┤ļŹö Ļ░Ģņłśļź╝ ņČöņĀĢĒĢśĻ│Ā ĻĘĖ ļĀłņØ┤ļŹö Ļ░ĢņłśņØś ņĀĢĒÖĢļÅäļź╝ ņé░ņĀĢĒĢśņŚ¼ ņĄ£Ļ│Ā ļō▒ĻĖēņŚÉņä£ņØś Z, ZDR, KDPļź╝ ņĄ£ņĀüņØś ĒÄĖĒīīļ│ĆņłśļĪ£ ļ│┤ņĢśļŗż. ņØ┤ļĢī ņé¼ņÜ®ļÉ£ ņĀĢļ¤ēņĀü ņĀĢĒÖĢļÅä ĻĖ░ņżĆņØĆ Eq. (6)Ļ│╝ Ļ░ÖņØĆ 1-NEņØ┤ļŗż. 1-NEļŖö 1ņŚÉņä£ NE (Normalized Error)ļź╝ ļ║Ć Ēøä ļ░▒ļČäļźĀĒÖö ĒĢ£ Ļ░Æņ£╝ļĪ£ 100%ņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ ĒÆłņ¦łņØ┤ ļåÆņØīņØä ņØśļ»ĖĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ 1-NEļŖö ĒÄĖņØśņÖĆ ļ│ĆļÅÖņä▒ņØ┤ ĒĢ©Ļ╗ś ņĀĢļ¤ēĒÖöļÉ£ Ļ░ÆņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ņĄ£ļīĆĻ░ÆņØä ļéśĒāĆļé┤ļŖö 1-NEņŚÉņä£ ĒÄĖņØśņÖĆ ļ│ĆļÅÖņä▒ņØ┤ Ēś╝ĒĢ®ļÉ£ ņśżņ░©Ļ░Ć ņĄ£ņåīĻ░Ć ļÉ©ņØä ņØśļ»ĖĒĢ£ļŗż.
ņŚ¼ĻĖ░ņä£, RiļŖö ļĀłņØ┤ļŹö Ļ░Ģņłśļ¤ēņØä, GiļŖö ņÜ░ļ¤ēĻ│ä Ļ░Ģņłśļ¤ēņØä ļéśĒāĆļéĖļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļŗ©ņØ╝ĒÄĖĒīīņØĖ ļ░śņé¼ļÅäļ¦īņØä ņĀüņÜ®ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ Yoon, Suk, et al. (2016)ņØś ļ░®ļ▓ĢņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļ░śņé¼ļÅäļ¦īņØä ņĪ░ņĀłĒĢ┤Ļ░Ćļ®░ ļĀłņØ┤ļŹö Ļ░ĢņłśņØś ņĀĢĒÖĢļÅäĻ░Ć ņĄ£ņĀüņØ┤ ļÉśļŖö ļĀłņØ┤ļŹö ļ░śņé¼ļÅäļź╝ Ļ▓░ņĀĢĒĢśņśĆļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ ļ░śņé¼ļÅäļź╝ 0 dBZņŚÉņä£ 20 dBZĻ╣īņ¦Ć 1 dBZ Ļ░äĻ▓®ņ£╝ļĪ£ Ļ░Ćņé░ĒĢśņśĆļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ┤ĆņĢģņé░ĻĖ░ņāüļĀłņØ┤ļŹöļź╝ ņĀüņÜ®ĒĢśņśĆļŗż. Ļ┤ĆņĢģņé░ ĻĖ░ņāüļĀłņØ┤ļŹöļŖö 1969ļģä ņłśļÅäĻČī ĻĖ░ņāüĻ░Éņŗ£ļź╝ ļ¬®ņĀüņ£╝ļĪ£ ļÅäņ×ģļÉ£ ĻĄŁļé┤ ņĄ£ņ┤łņØś ĻĖ░ņāüļĀłņØ┤ļŹöņØ┤ļŗż. Ļ┤ĆņĢģņé░ĻĖ░ņāüļĀłņØ┤ļŹöļŖö ņĄ£ņ┤ł ļÅäņ×ģ Ēøä 1988ļģäĻ│╝ 2005ļģäņŚÉ Ļ░üĻ░ü Cļ░┤ļō£ņÖĆ Sļ░┤ļō£ ļÅäĒöīļ¤¼ ļĀłņØ┤ļŹöļĪ£ ĻĄÉņ▓┤ļÉśņŚłļŗż. Ļ┤ĆņĢģņé░ĻĖ░ņāüļĀłņØ┤ļŹöĻ░Ć Sļ░┤ļō£ ļĀłņØ┤ļŹöļĪ£ ĻĄÉņ▓┤ļÉśņ¢┤ Ļ┤ĆņĖĪņØ┤ Ļ░£ņŗ£ļÉ£ ņŗ£ņĀÉņØ┤ 2005ļģä 12ņøöņØ┤Ļ│Ā 2016ļģäļČĆĒä░ ņØ┤ņżæĒÄĖĒīīļĀłņØ┤ļŹöļĪ£ ĻĄÉņ▓┤ļÉśņŚłĻĖ░ ļĢīļ¼ĖņŚÉ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 2006ļģäļČĆĒä░ 2015ļģäĻ╣īņ¦Ć 6ņøöņŚÉņä£ 10ņøö ņé¼ņØ┤ņØś 189Ļ░£ Ļ░Ģņłś ņé¼ļĪĆļź╝ ņĀüņÜ®ĒĢśņśĆļŗż.
ļĀłņØ┤ļŹö ļ░śņé¼ļÅäļŖö 1 km ├Ś 1 km Ļ│ĄĻ░ä ĒĢ┤ņāüļÅäņÖĆ 10ļČä ņŗ£Ļ░ä ĒĢ┤ņāüļÅäņØś 1.5 km CAPPIļĪ£ Ēæ£ņČ£ļÉśņŚłĻ│Ā ļĀłņØ┤ļŹö Ļ░ĢņÜ░ Ļ░ĢļÅäļĪ£ ļ│ĆĒÖśĒĢśĻĖ░ ņ£äĒĢ┤ A=300, b=1.4ļź╝ ņĀüņÜ®ĒĢśņśĆļŗż. 10ļČä ļŗ©ņ£äņØś ļĀłņØ┤ļŹö Ļ░ĢņÜ░ Ļ░ĢļÅäļŖö 1ņŗ£Ļ░ä ļŗ©ņ£äņØś ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļ¤ēņ£╝ļĪ£ ļ│ĆĒÖśĒĢśņśĆĻ│Ā ņØ┤ļ¤¼ĒĢ£ 1ņŗ£Ļ░ä ļŗ©ņ£äņØś ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļ¤ēņØĆ ļĀłņØ┤ļŹö ļ░śĻ▓Į 100 km ņØ┤ļé┤ņØś AWS 1ņŗ£Ļ░ä ļŗ©ņ£ä Ļ░ĢņÜ░ļ¤ēĻ│╝ ļ╣äĻĄÉĒĢśņśĆļŗż(Fig. 1).
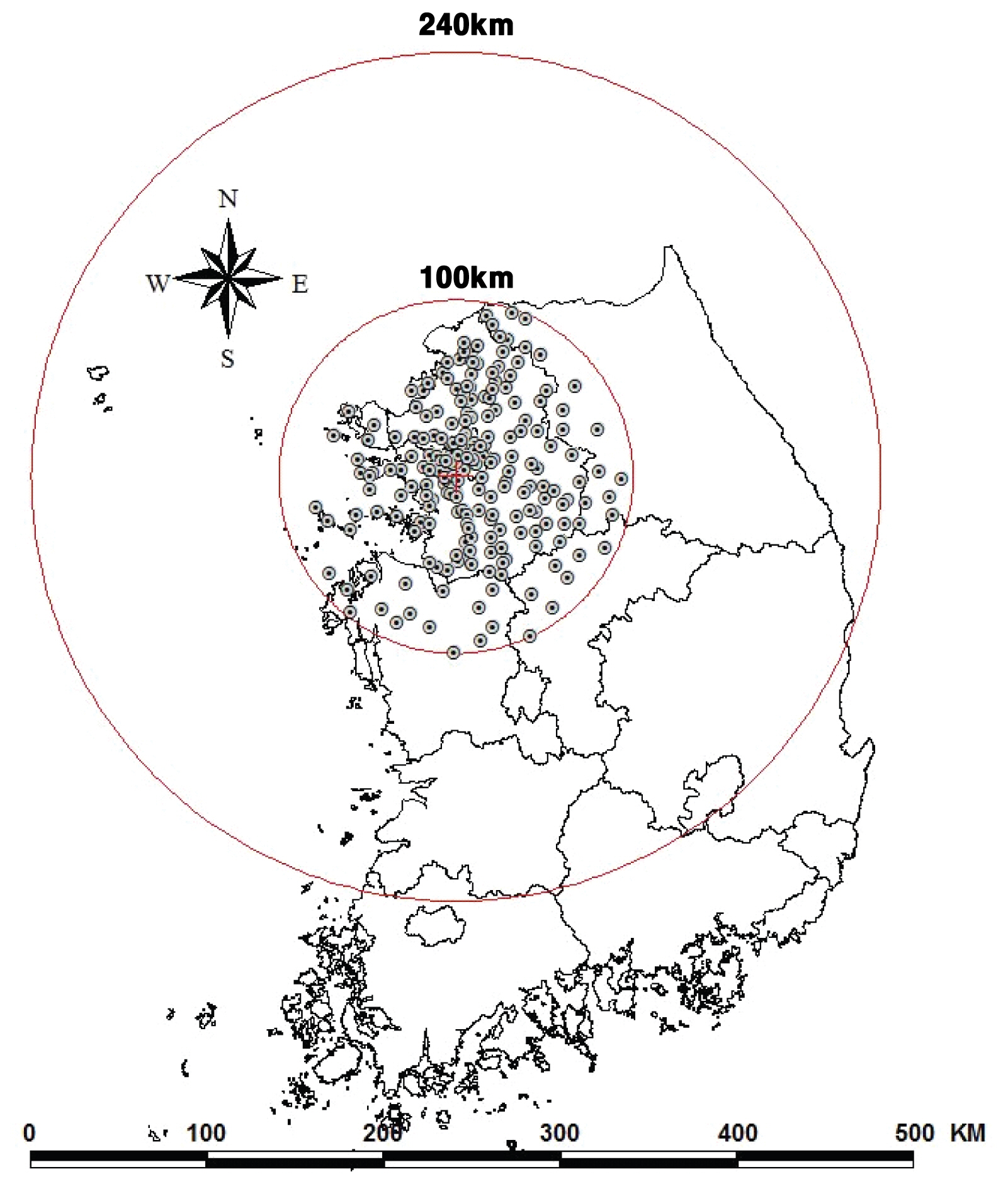
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ┤Ø 189Ļ░£ņØś Ļ░Ģņłś ņé¼ļĪĆļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņśżņ░©ļź╝ ņĀĢļ¤ēĒÖöĒĢśņśĆļŗż. Fig. 2(a)ļŖö 189Ļ░£ Ļ░Ģņłś ņé¼ļĪĆņŚÉ ļīĆĒĢ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņÖĆ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņØś ņāüĻ┤ĆĻ│äņłśļź╝ ļéśĒāĆļéĖļŗż. ĻĘĖļ”╝ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņÖĆ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņØś ņāüĻ┤ĆĻ│äņłśļŖö 0.6 ņØ┤ņāüņ£╝ļĪ£ ĻĘĖ ļ│Ćņłśļōż Ļ░äņØś ņāüĻ┤Ćņä▒ņØ┤ ļåÆĻ▓ī ļéśĒāĆļéśĻ│Ā ņ׳ļŗż. Fig. 2(b)ļŖö ņÜ░ļ¤ēĻ│ä ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēĻ│╝ ļĀłņØ┤ļŹö ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēņØś ņé░ņĀÉļÅäļź╝ ļéśĒāĆļéĖļŗż. ņĀäņ▓┤ Ļ░Ģņłś ņé¼ļĪĆņŚÉ ļīĆĒĢ£ ņÜ░ļ¤ēĻ│äĻ░ĢņÜ░ņØś ĒÅēĻĘĀņØĆ 4.79 mmņØ┤ļ®░, ļĀłņØ┤ļŹöĻ░ĢņÜ░ņØś ĒÅēĻĘĀņØĆ 1.78 mmļĪ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņŚÉ ļ╣äĒĢ┤ ņĀĢļ¤ēņĀüņ£╝ļĪ£ 37% ņĀĢļÅäļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ļŗż.
Fig. 3ņØĆ ņÜ░ļ¤ēĻ│ä ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēĻ│╝ ļĀłņØ┤ļŹö ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēņŚÉ ļö░ļźĖ ņČöņĀĢ ĒÄĖņØś B ^ B ^ B ^ B ^ B ^ B ^ B ^
ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö Eq. (5)ļĪ£ļČĆĒä░ ņé░ņĀĢĒĢĀ ņłś ņ׳ļŗż.
Eq. (5)ņØś BļŖö Fig. 3ņŚÉņä£ ņé░ņĀĢĒĢ£ B ^ Žā z 2
ļĀłņØ┤ļŹö ļ░śņé¼ļÅäļŖö Fig. 4ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ņé░ņĀĢļÉ£ ļ░śņé¼ļÅäņØś ĒÄĖņØśļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ│┤ņĀĢĒĢĀ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤ 2013ļģä 7ņøö 22ņØ╝ ĒśĖņÜ░ņé¼ļĪĆņØś B ^
ĒĢ£ĒÄĖ ļ│┤ņĀĢ ņØ┤ĒøäņŚÉļŖö ĻĘĖ ĒÄĖņØśĻ░Ć ļŗżņåī Ļ░£ņäĀļÉśņ¢┤ 73.543% 1-NE Ļ░Æņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņØ┤ļŖö ĒÄĖņØś ļ│┤ņĀĢņ£╝ļĪ£ 44.296%ņØś Ļ░£ņäĀĒÜ©Ļ│╝ļź╝ ļ│┤ņØĖ Ļ▓░Ļ│╝ņØ┤ļŗż. ņĢ×ņä£ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░Ļ░Ć ņĄ£ļīĆļĪ£ ļéśĒāĆļé£ ņ¦ĆņĀÉņŚÉņä£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö 77.25 mmļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ņ£╝ļ®░ ņØ┤ļŖö ĻĘĖ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņØś ļīĆļץ 69.9%ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņ¢æņØ┤ļŗż. ĻĘĖļ¤¼ļéś ņØ┤ļ¤¼ĒĢ£ ĒÄĖņØś ļ│┤ņĀĢ ņØ┤ĒøäņŚÉļÅä ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ņŚ¼ņĀäĒ׳ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņŚÉ ļ╣äĒĢ┤ ņ×æĻ▓ī ļéśĒāĆļéśĻ│Ā ņ׳ļŗż. ņØ┤ļŖö ņĢ×ņä£ Eq. (5)ņŚÉņä£ ņśżņ░©ļČäņé░ Žā z 2
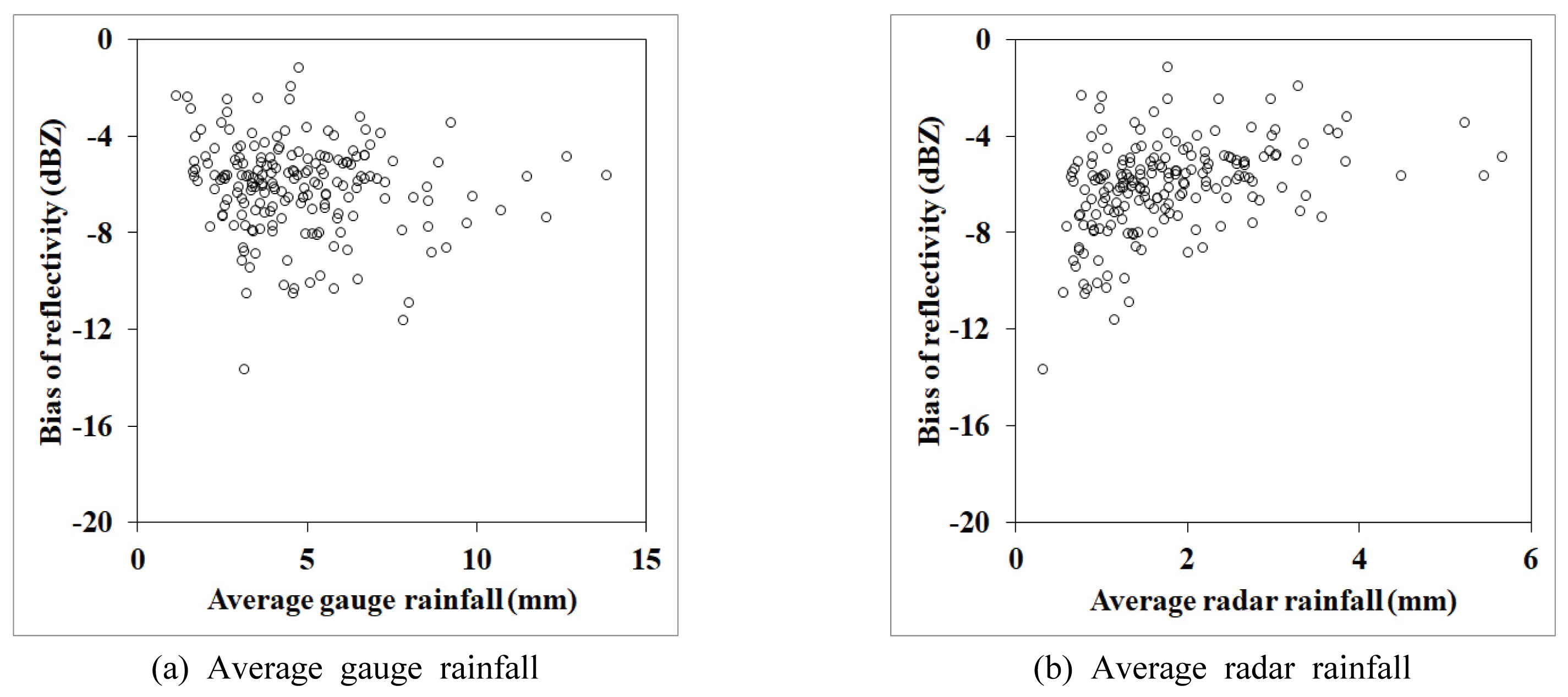
Fig. 6ņØĆ Yoon, Suk, et al. (2016)ņŚÉņä£ ņĀüņÜ®ĒĢ£ Ļ▓ĮĒŚśņĀü ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņé░ņĀĢļÉ£ ņĪ░ņĀłļō▒ĻĖēņŚÉ ļö░ļźĖ ļĀłņØ┤ļŹöĻ░ĢņÜ░ļ¤ēņØś ņĀĢĒÖĢļÅäņØ┤ļŗż. ņĀüņÜ®ļÉ£ ĒśĖņÜ░ņé¼ļĪĆļŖö 2013ļģä 7ņøö 22ņØ╝ ņé¼ļĪĆņØ┤ļŗż. ĻĘĖļ”╝ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļĀłņØ┤ļŹöĻ░ĢņÜ░ļ¤ēņØś ņĀĢĒÖĢļÅäļŖö ņĪ░ņĀłļō▒ĻĖēņØ┤ ļåÆņĢäņ¦ÉņŚÉ ļö░ļØ╝ ņ”ØĻ░ĆĒĢśļŗż 10 ļō▒ĻĖēņŚÉņä£ ņĄ£Ļ│ĀĻ░ÆņØä ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā 10ļō▒ĻĖē ņØ┤ĒøäļČĆĒä░ļŖö ņĀĢĒÖĢļÅäĻ░Ć Ļ░ÉņåīĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ļŗż. ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ 10 dBZļź╝ Ļ░Ćņé░ĒĢ┤ņĢ╝ ņĄ£ņåīņØś ņśżņ░©ļź╝ ļéśĒāĆļé┤ļ»ĆļĪ£ ņØ┤ ĒśĖņÜ░ņé¼ļĪĆņŚÉņä£ Ļ▓ĮĒŚśņĀüņ£╝ļĪ£ ņé░ņĀĢļÉ£ ļĀłņØ┤ļŹöĒÄĖņØśļŖö -10 dBZ ņ×äņØä ņØśļ»ĖĒĢ£ļŗż. ņØ┤ļŖö ņĢ×ņä£ ņśżņ░©ļČäņé░ņØ┤ 0ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢ£ Ļ▓ĮņÜ░ņŚÉņä£ ņé░ņĀĢļÉ£ -7.402 dBZļ│┤ļŗż 2.598 dBZ ļŹö ļé«ņØĆ Ļ░ÆņØ┤ļŗż. ņØ┤ļ¤¼ĒĢ£ 2.598 dBZ ļČĆļČäņØś ĒÄĖņØśļŖö ņĢ×ņä£ ņäżļ¬ģĒĢ£ ļ░öņÖĆ Ļ░ÖņØ┤ ņśżņ░©ļČäņé░ņ£╝ļĪ£ ņØĖĒĢ£ Ļ▓āņØ┤ļŗż. Eq. (5)ļĪ£ļČĆĒä░ ņśżņ░©ļČäņé░ņØä ņŚŁņ£╝ļĪ£ ņČöņĀĢĒĢśļ®┤ ņśżņ░©ļČäņé░ņØĆ 5.6212 dBZ2ļĪ£ ņČöņĀĢļÉ£ļŗż.
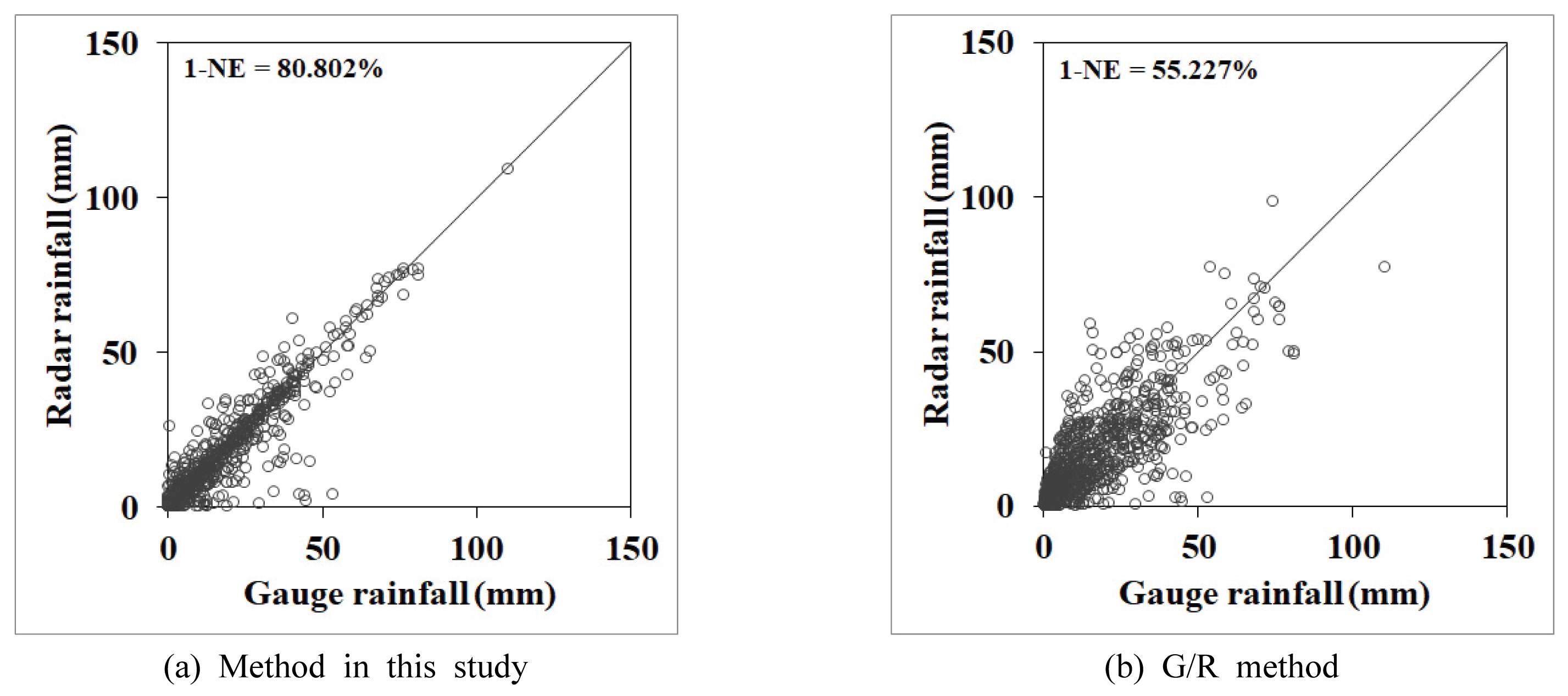
Fig. 7(a)ņØĆ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņÖĆ ņŗżņĀ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśĻ░Ć ļ│┤ņĀĢļÉ£ ļĀłņØ┤ļŹöĻ░ĢņÜ░ņÖĆņØś ņé░ņĀÉļÅäļź╝ ļéśĒāĆļéĖļŗż. ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ņĀĢĒÖĢļÅäļŖö 80.802%ņØś 1-NE Ļ░ÆņØä ļéśĒāĆļé┤Ļ│Ā ņ׳ņ£╝ļ®░ ņØ┤ļŖö ņśżņ░©ļČäņé░ņØä 0ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢ£ Ļ▓ĮņÜ░ņŚÉ ļ╣äĒĢ┤ 7.259% ļåÆņØĆ Ļ░ÆņØ┤ļŗż. ņØ┤ Ļ▓ĮņÜ░ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░Ļ░Ć ņĄ£ļīĆļĪ£ ļéśĒāĆļé£ ņ¦ĆņĀÉņŚÉņä£(110.5 mm)ņŚÉņä£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö 109.23 mmļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ņ£╝ļ®░ ņØ┤ļŖö ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņØś ļīĆļץ 98.9%ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņ¢æņØ┤ļŗż. ĻĘĖļ”╝ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ĒÄĖņØśļŖö Ļ▒░ņØś ņĀ£Ļ▒░ļÉśņŚłĻ│Ā ļ¼┤ņ×æņ£ä ņśżņ░©ļ¦īņØ┤ ļé©ņĢä ņ׳ļŗż. ĒĢ£ĒÄĖ Fig. 7(b)ņØĆ ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņÖĆ G/Rļ╣äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ│┤ņĀĢļÉ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ņé░ņĀÉļÅäļź╝ ļéśĒāĆļéĖļŗż. G/Rļ╣äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ│┤ņĀĢļÉ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ņ¢æņĀüņ£╝ļĪ£ ņÜ░ļ¤ēĻ│äĻ░ĢņÜ░ņÖĆ Ļ▒░ņØś ņ£Āņé¼ĒĢ┤ņĪīņØīņØä ņĢī ņłś ņ׳ļŗż. ņ”ē, ĒÄĖņØśļŖö Ļ▒░ņØś ņĀ£Ļ▒░ļÉśņŚłļŗż. ĻĘĖļ¤¼ļéś ļ¼┤ņ×æņ£ä ņśżņ░©Ļ░Ć ļäłļ¼┤ Ēü¼Ļ▓ī ļéśĒāĆļéśĻ│Ā ņ׳ņ¢┤ 1-NEņØś Ļ░ÆļÅä ļ░śņé¼ļÅä ĒÄĖņØśļź╝ ļ│┤ņĀĢĒĢ£ Ļ▓ĮņÜ░ņŚÉ ļ╣äĒĢ┤ 25.575%ļéś ņ×æņØĆ 55.227%ņŚÉ ļČłĻ│╝ĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ▓░Ļ│╝ļĪ£ļČĆĒä░ ļ│Ė ņŚ░ĻĄ¼ņØś ļ░®ļ▓Ģļ│┤ļŗż G/Rļ╣äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ│┤ņĀĢĒĢśļŖö Ļ▓ĮņÜ░ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ĒÄĖņØśļŖö ņĀ£Ļ▒░ ļÉśĻ│Ā ņ׳ņ£╝ļéś ņśżņ░©ņŚÉ ļīĆĒĢ£ ļ│ĆļÅÖņä▒ņØ┤ ļåÆņĢäņ¦ĆĻ│Ā ņ׳ņØīņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
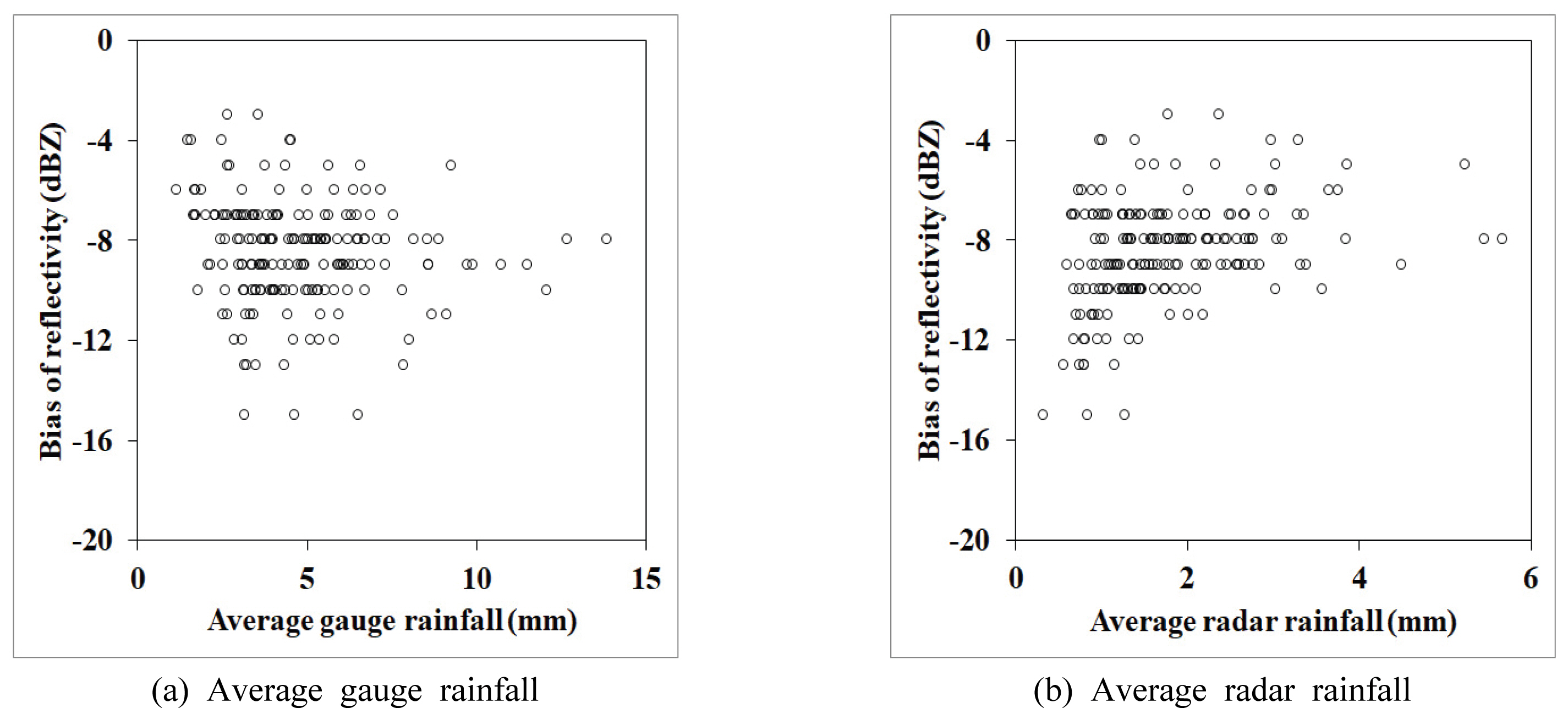
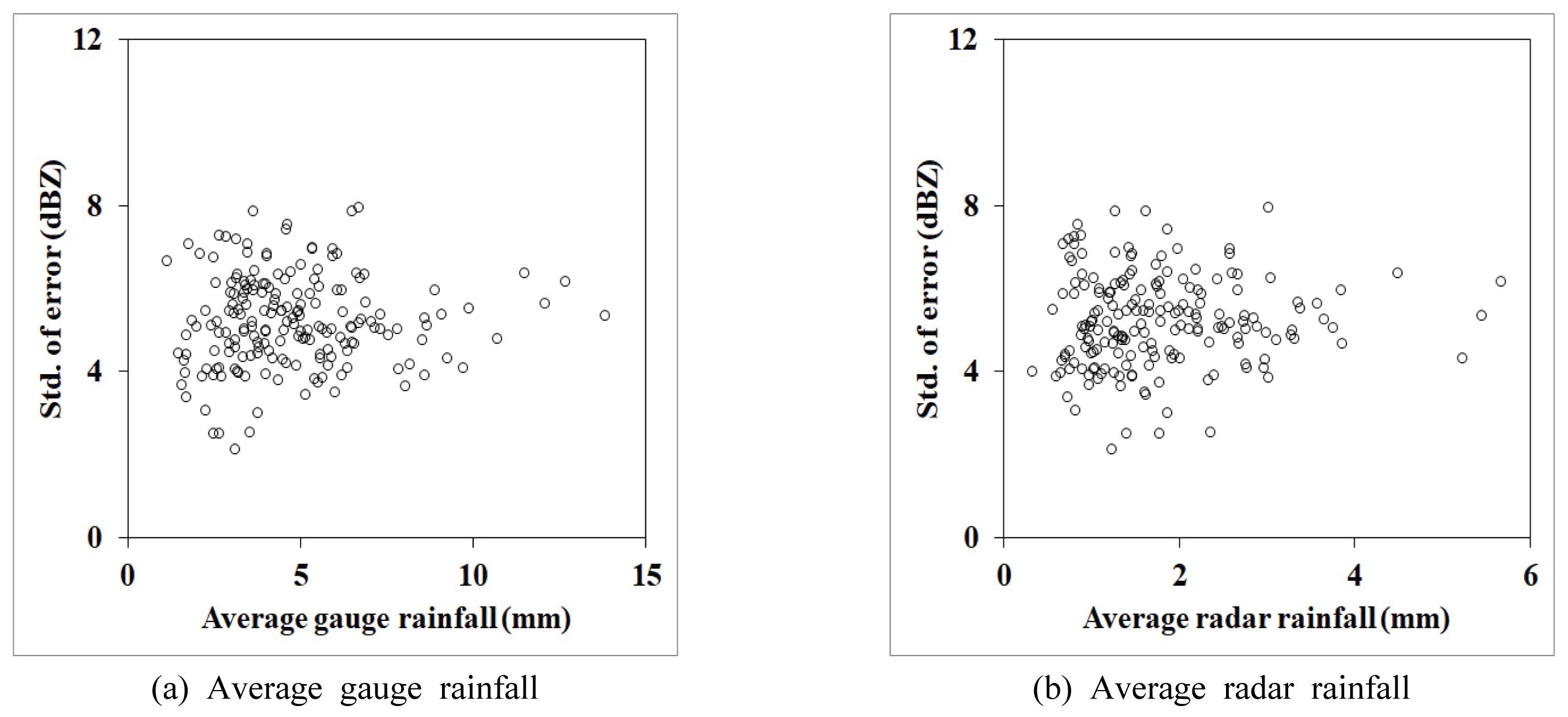
ņĀäņ▓┤ Ļ░Ģņłśņé¼ļĪĆņŚÉ ļīĆĒĢ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņŗżņĀ£ ĒÄĖņØśļź╝ ĻĄ¼ĒĢ£ Ļ▓░Ļ│╝Ļ░Ć Fig. 8Ļ│╝ Ļ░Öļŗż. ņĀäņ▓┤ņĀüņ£╝ļĪ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö ŌĆō3 dBZņŚÉņä£ ŌĆō15 dBZļĪ£ ļéśĒāĆļé¼ļŗż. ĻĘĖļ”╝ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļĀłņØ┤ļŹö ļ░śņé¼ļÅä ĒÄĖņØśņØś Ļ▓ĮĒ¢źņä▒ņØĆ ņĢ×ņä£ ņśżņ░©ļČäņé░ņØ┤ 0ņØĖ Ļ▓ĮņÜ░ņÖĆ Ēü¼Ļ▓ī ļŗ¼ļØ╝ņ¦ä Ļ▓āņØĆ ņŚåļŗż. ļŗżļ¦ī ĻĘĖ ĒÄĖņØśĻ░Ć ņĢ×ņäĀ Ļ▓ĮņÜ░ļ│┤ļŗż Ēü¼Ļ▓ī ļéśĒāĆļéśĻ│Ā ņ׳ņØä ļ┐ÉņØ┤ļŗż. ĒĢ£ĒÄĖ Fig. 9ļŖö ņÜ░ļ¤ēĻ│ä ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēĻ│╝ ļĀłņØ┤ļŹö ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēņŚÉ ļö░ļźĖ ņśżņ░©ļČäņé░ņØä ļéśĒāĆļéĖļŗż. ĻĘĖļ”╝ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ņśżņ░©ļČäņé░ņØĆ 22Ōł╝82 dBZ2 ņé¼ņØ┤ņŚÉņä£ ļ│ĆļÅÖĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ļŗż.
ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļź╝ ļ│┤ņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ĒÄĖņØśņØś Ēü¼ĻĖ░ļ¦īĒü╝ņØä ļŹöĒĢ┤ņŻ╝ļ®┤ ļÉ£ļŗż. ĻĘĖļ¤¼ļéś ņśżņ░©ļČäņé░ņØĆ ļ¼┤ņ×æņ£ä ņśżņ░©ļĪ£ ļéśĒāĆļéśļŖö ļČĆļČäņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ĻĘĖ ņĀ£Ļ▒░Ļ░Ć ĒÄĖņØśļź╝ ņĀ£Ļ▒░ĒĢśļŖö Ļ▓āĻ│╝ Ļ░ÖņØ┤ ņēĮņ¦Ć ņĢŖļŗż. ņśłļź╝ ļōżņ¢┤ Ļ┤ĆņĢģņé░ļĀłņØ┤ļŹöņØś Ļ▓ĮņÜ░ ļ░śņé¼ļÅäņŚÉ 2013ļģä 7ņøö 22ņØ╝ ĒśĖņÜ░ņé¼ļĪĆņØś ĒÄĖņØś 7.402 dBZļź╝ ļŹöĒĢ┤ņŻ╝ļ®┤ Eq. (5)ņŚÉņä£ BļŖö 1ņØ┤ ļÉśņ¢┤ ņÜ░ņĖĪ ņ▓½ ļ▓łņ¦Ė ĒĢŁņØĆ 0ņØ┤ ļÉśļéś Žā z 2 B ^
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦Ćļé£ 10ļģä ļÅÖņĢł ĻĄŁļé┤ņŚÉņä£ ņĀ£ĻĖ░ļÉśņ¢┤ ņś© ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś Ļ│╝ņåīĒĢ£ ļ¼ĖņĀ£ņĀÉņŚÉ ļīĆĒĢ£ ĒĢ┤Ļ▓░ņ▒ģņØä ņĀ£ņŗ£ĒĢśĻĖ░ ņ£äĒĢ┤ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņŚÉ ļé┤ņ×¼ļÉśņ¢┤ ņ׳ļŖö ņśżņ░©ļź╝ ņĀĢļ¤ēĒÖö ĒĢśņśĆļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ 2006ļģäļČĆĒä░ 2015ļģäĻ╣īņ¦Ć 6ņøöņŚÉņä£ 10ņøö ņé¼ņØ┤ņØś 189Ļ░£ Ļ░Ģņłś ņé¼ļĪĆļź╝ ņĀüņÜ®ĒĢśņśĆņ£╝ļ®░ ĻĘĖ Ļ▓░Ļ│╝ļŖö ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņ▓½ ļ▓łņ¦Ė, 189Ļ░£ ņĀäņ▓┤ Ļ░Ģņłś ņé¼ļĪĆņŚÉ ļīĆĒĢ£ ņÜ░ļ¤ēĻ│äĻ░ĢņÜ░ņØś ĒÅēĻĘĀņØĆ 4.79 mmņØ┤Ļ│Ā ļĀłņØ┤ļŹöĻ░ĢņÜ░ņØś ĒÅēĻĘĀņØĆ 1.78 mmļĪ£, ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņŚÉ ļ╣äĒĢ┤ ņĀĢļ¤ēņĀüņ£╝ļĪ£ 37% ņĀĢļÅäņŚÉ ļČłĻ│╝ĒĢśņśĆļŗż. ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ņČöņĀĢ ĒÄĖņØś B ^ B ^
ļæÉ ļ▓łņ¦Ė, ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö ņÜ░ļ¤ēĻ│äņØś ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēņØ┤ ņ×æņØĆ ļČĆļČäņŚÉņä£ļŖö ļ│ĆļÅÖņä▒ņØ┤ Ēü¼Ļ▓ī ļéśĒāĆļéśļŗż ĻĘĖ ĒÅēĻĘĀ Ļ░ĢņÜ░ļ¤ē Ļ░ÆņØ┤ ņ╗żņ¦łņłśļĪØ ļīĆļץ -5Ōł╝-6 dBZ ņé¼ņØ┤ Ļ░Æņ£╝ļĪ£ ņłśļĀ┤ĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ĒĢ£ĒÄĖ ļĀłņØ┤ļŹöņØś ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēņŚÉ ļö░ļźĖ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö ļĀłņØ┤ļŹö ĒÅēĻĘĀĻ░ĢņÜ░ļ¤ēņØ┤ ņ×æņØĆ Ļ▓ĮņÜ░ ĻĘĖ ĒÄĖņØśĻ░Ć ļ¦żņÜ░ Ēü¼Ļ▓ī ļéśĒāĆļéśļ®░ Ēü░ Ļ▓ĮņÜ░ņŚÉņä£ļŖö ļīĆļץ -5Ōł╝-6 dBZ ņĀĢļÅäļĪ£ ņłśļĀ┤ĒĢśņśĆļŗż. ņĀäņ▓┤ņĀüņ£╝ļĪ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśļŖö ŌĆō1 dBZņŚÉņä£ ŌĆō14 dBZļĪ£ ļéśĒāĆļé¼ļŗż.
ņäĖ ļ▓łņ¦Ė, ņÜ░ļ¤ēĻ│ä Ļ░ĢņÜ░ņÖĆ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļĪ£ļČĆĒä░ ņČöņĀĢļÉ£ B ^ Žā z 2
ļäż ļ▓łņ¦Ė, Ļ▓ĮĒŚśņĀü ļ░®ļ▓Ģņ£╝ļĪ£ ņČöņĀĢļÉ£ ņŗżņĀ£ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ĒÄĖņØśņÖĆ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ņČöņĀĢ ĒÄĖņØś B ^
ļĀłņØ┤ļŹö Ļ░ĢņÜ░ļŖö ņłśļ¼Ė ļČäņĢ╝ņŚÉņä£ņØś ļåÆņØĆ ĒÖ£ņÜ® Ļ░ĆļŖźņä▒ņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ĻĘĖ ņĀĢĒÖĢļÅäņŚÉ ļīĆĒĢ£ ļ¼ĖņĀ£ņĀÉņ£╝ļĪ£ ņ×ÉļŻī ĒÖ£ņÜ®ņä▒ņŚÉ ļīĆĒĢ£ ņØśĻĄ¼ņŗ¼ņØ┤ ņĀ£ĻĖ░ļÉśņ¢┤ ņÖöļŗż. ĻĘĖļ¤¼ļéś ļ│Ė ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ļĀłņØ┤ļŹö ļ░śņé¼ļÅäņØś ņśżņ░©ļź╝ ņĀĢļ¤ēĒÖöĒĢśĻ│Ā ļ│┤ņĀĢĒĢ£ļŗżļ®┤ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņØś ĒÖ£ņÜ®ņä▒ņØĆ ļ¦żņÜ░ ļåÆņĢäņ¦ł Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆļÉ£ļŗż.
Ļ░Éņé¼ņØś ĻĖĆ
ļ│Ė ņŚ░ĻĄ¼ļŖö ĻĄŁĒåĀĻĄÉĒåĄļČĆ ļ¼╝Ļ┤Ćļ”¼ņŚ░ĻĄ¼ņé¼ņŚģņØś ņŚ░ĻĄ¼ļ╣äņ¦ĆņøÉ(18AWMP-B079625-05)ņŚÉ ņØśĒĢ┤ ņłśĒ¢ēļÉśņŚłņŖĄļŗłļŗż.
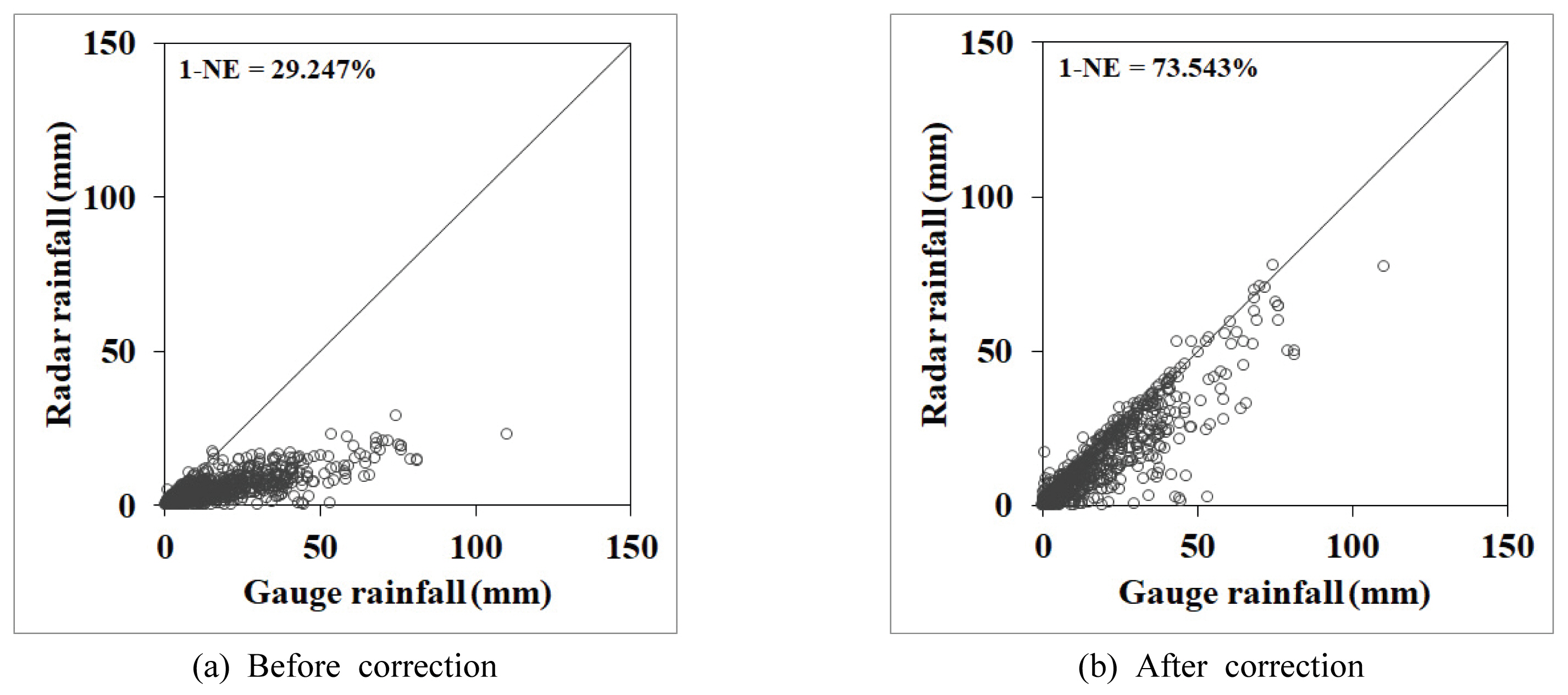
Fig.┬Ā5
Scatter Plots Between Gauge Rainfall and Radar Rainfall Before and After Correction for Reflectivity Bias
References
Atlas
,
D
(
2002
)
Radar calibration: Some simple approaches
.
Bulletin of the American Meteorological Society
, Vol.
83
, pp.
1313
-
1316
.

Gosset
,
M
,
Zahiri
,
EP
, and
Moumouni
,
S
(
2010
)
Rain drop size distribution variability and impact on X-band polarimetric radar retrieval: Results from the AMMA campaign in Benin
.
Quarterly Journal of the Royal Meteorological Society
, Vol.
136
, No.
s1
, pp.
243
-
256
.

Kim
,
J
, and
Yoo
,
C
(
2014
)
Using extended Kalman filter for real-time decision of parameters of Z-R relationship
.
Journal of Korea Water Resources Association
, Vol.
47
, No.
2
, pp.
119
-
133
.

Kim
,
K
,
Choi
,
J
, and
Yoo
,
C
(
2008
)
Synthesis of radar measurements and ground measurements using the successive correction method (SCM)
.
Journal of Korea Water Resources Association
, Vol.
41
, No.
7
, pp.
681
-
692
.

Koistinen
,
J
,
Michelson
,
DB
,
Hohti
,
H
, and
Peura
,
M
(
2004
).
Operational measurement of precipitation in cold climates
.
Weather Radar
. In:
Meischner
P
, ed.
Springer
,
Berlin, Heidelberg
: p
78
-
114
.

Krajewski
,
WF
(
1987
)
Cokriging of radar-rainfall and rain gage data
.
Journal of Geophysical Research
, Vol.
92
, No.
D8
, pp.
9571
-
9580
.

Krajewski
,
WF
, and
Smith
,
JA
(
2002
)
Radar hydrology: Rainfall estimation
.
Advances in Water Resources
, Vol.
25
, No.
8ŌĆō12
, pp.
1387
-
1394
.

MRI (Meteorological Research Institute)
(
2004
).
Development of METRI X-Band Doppler weather radar operations and radar data analysis technique (IV)
.
Seoul, Korea
: p
224
.

Park
,
SG
, and
Lee
,
GW
(
2010
)
Calibration of radar reflectivity measurements from the KMA operational radar network
.
Asia-Pacific Journal of Atmospheric Sciences
, Vol.
46
, No.
3
, pp.
243
-
259
.

Seo
,
BC
, and
Krajewski
,
WF
(
2011
)
Investigation of the scale-dependent variability of radar-rainfall and rain gauge error covariance
.
Advances in Water Resources
, Vol.
34
, No.
1
, pp.
152
-
163
.

Seo
,
DJ
,
Krajewski
,
WF
, and
Bowles
,
DS
(
1990
)
Stochastic interpolation of rainfall data from rain gages and radar using cokriging: 1. Design of experiments
.
Water Resources Research
, Vol.
26
, No.
3
, pp.
469
-
477
.

Suk
,
M
,
Nam
,
K
,
Kim
,
Y
, and
Oh
,
S
(
2005
)
Estimation of quantitative rain intensity from radar reflectivities using a window probability matching method
.
Asia-Pacific Journal of Atmospheric Sciences
, Vol.
41
, No.
1
, pp.
123
-
138
.

WRC (Weather Radar Center)
(
2015
).
Development and application of cross governmental dual-pol. radar harmonization
.
Seoul, Korea
.

Yoo
,
C
,
Park
,
C
,
Yoon
,
J
, and
Kim
,
K
(
2013
)
Interpretation of mean-field bias correction of radar rain rate using the concept of linear regression
.
Hydrological Processes
, Vol.
28
, No.
19
, pp.
5081
-
5092
.

Yoo
,
C
,
Yoon
,
J
,
Kim
,
J
, and
Ro
,
Y
(
2016
)
Evaluation of the gap filler radar as an implementation of the 1.5 km CAPPI data in Korea
.
Meteorological Applications
, Vol.
23
, pp.
76
-
88
.

Yoon
,
J
(
2013
).
Studies on the error structure of the radar reflectivity to estimate the bias of the radar rain rate
.
PhD dissertation
.
Korea University
;
Seoul, Korea
.

Yoon
,
J
,
Choi
,
J
,
Yoo
,
C
, and
Kim
,
K
(
2016
)
The runoff uncertainty caused by the mismatch between the radar rain rate and the topographical information data
.
KSCE Journal of Civil Engineering
, Vol.
20
, No.
2
, pp.
960
-
970
.