수문학적 예측을 위한 딥러닝기반 인공신경망의 최적화 알고리즘 비교: 남강댐 일유출량을 사례를 중심으로
Comparison of Optimization Algorithms in Deep Learning-Based Neural Networks for Hydrological Forecasting: Case Study of Nam River Daily Runoff
Article information
Abstract
인공신경망은 수문기상학적 변수들에 대해 강우유출 시뮬레이션, 통계학적 상세화 등에 널리 사용되어 왔다. 최근에는 인공신경망을 기반으로 한 딥러닝 기술이 혁신적으로 발전되어오고 있다. 딥러닝의 성능을 향상시키기 위해서, 인공신경망에 들어가는 매개변수를 추정하기 위한 다양한 최적화 기법들이 개발되어 왔다. 이러한 다양한 최적화 기법 중에서 수문학적 적용에 가장 유용한 방법을 선정해 주는 것은 매우 중요한 문제일 것이다. 따라서 본 연구에서는 기존에 개발된 SGD와 더불어 최근에 개발된 Adagrad, RMSprop, Adadelta, Adam, and Nadam의 기법들을 남강댐 유역의 강우-유출시뮬레이션에 적용하여 가장 좋은 최적화 기법을 찾는 연구를 실시하였다. 연구결과 성능에 뚜렷한 큰 차이는 없었으나 기존의 방법보다 Adam과 Nadam이 보다 좋은 성능을 보이고 있음을 확인할 수 있었다. 이러한 조그만 차이라 할지라도 많은 매개변수 추정을 여러차례 반복해야 하는 딥러닝의 특성상 중요한 결과로 여겨진다. 따라서, 본 연구는 수문기상분야에서 딥러닝을 위한 새로운 매개변수 추정 기법을 실험하였고 나온 결과들을 토대로 딥러닝의 다양한 수문학적 적용사례가 나오길 기대한다.
Trans Abstract
Neural networks have been widely used in forecasting hydrometeorological variables such as rainfall-runoff simulation and statistical downscaling. Furthermore, deep learning approaches have been developed in recent decades. To improve the performance in deep learning, many optimization algorithms have been proposed in literature to estimate the weights of connections between nodes. An essential need exists to provide information about how the proposed optimization algorithms behave in different applications so that a reasonable algorithm can be selected for a particular application. In the current study, we used rainfall datasets of the Nam River basin to test several available algorithms used in runoff forecasting such as Stochastic Gradient Descent (SGD), Adaptive Gradient Algorithm (Adagrad), Root-Mean-Square prop (RMSprop), Adaptive Delta (Adadelta), Adaptive Moment Estimation (Adam), and Adam with Nesterov Momentum (Nadam). Among these, Adam and Nadam, which are the most recently developed, presented better performance in predicting runoff even though the difference was limited. This difference might be critical when using modeling procedures that must be repeated numerous times, such as deep learning. Further extensive studies might refine the parameter estimation algorithm and allow the use of deep learning for hydrometeorological applications with the tested recent optimization algorithms.
1. 서 론
인공신경망을 통한 기계학습은 다양한 분야에서 널리 이용되고 있다. 뿐만아니라 최근에는 Convolution Neural Net (CNN)이라는 딥러닝 기법을 통하여 이미지 인식, 음성인식, 자연어 처리 등의 비약적인 발전을 이루고 있다.
수문학 분야에서도 인공신경망을 통하여 강우예측, 자료보정, 기후자료 상세화 등 다양한 문제점을 해결해 나가고 있다(Kim and Bae, 2017; Nagaraja et al., 2018; Sachindra et al., 2018; Tan et al., 2018; Tao et al., 2018).
딥러닝에 대한 수문학적 적용은 아직 폭넓게 이루어지지는 않고 있으나 조금씩 적용성이 확대되어 가고 있는 실정이다. Tran and Song (2017)은 Recurrent neural network (RNN), RNN-BPTT (Backpropagation Through Time), LSTM (Long Short Term Memory)을 이용하여 하천유량, 강수량, 기존의 수위자료를 바탕으로 수위예측 등을 실시하여 LSTM이 가장 우수한 성능을 가짐을 증명하였다.
이와 더불어 딥러닝 내의 인공신경망에는 수많은 매개변수들이 들어가는데 이를 추정하기 위해서 오차역전파 (backpropagation)을 바탕으로 최적화 알고리즘이 적용된다. 일반적으로는 확률적경사하강법을 사용하여 왔으나 최근에 들어서 이 방법을 개선하기 위해 다양한 연구들이 시도되고 있다.
따라서, 본 연구에서는 최근에 개발된 인공신경망에서의 다양한 최적화 알고리즘들을 비교하고 수문학적 유출에 대해서 가장 효과가 있는 알고리즘을 찾기 위한 연구를 시도하였다.
2. 인공신경망(Artifical Neural Network)
인공신경망은 여러층(multilayer)으로 구성된 구조를 가지고 있는데 입력층(input layer), 출력층(output layer), 및 은닉층(hidden layer)으로 구성되어 있다. 각각의 층에는 뉴런들이 존재하고 이를 연결시키는 구조로 되어 있다. 각각의 층에서 연결강도가 매개변수들로 설정되고 이전 층의 값들이 연결강도를 매개변수로한 가중선형 형식으로 입력되고 비선형 형태의 함수를 통해 출력된다. 이를 반복해서 최종 출력층까지 도달하게 된다. 다층의 은닉층도 가능하나 본 연구에서는 단일 은닉층을 기반으로 하였다.
식으로 표시하면 다음과 같다. 먼저 입력변수는 n개의 뉴런을 가지고 (xi, i=1,...,n) 은닉층은 p개의 뉴런을 갖고(zj, j=1,..,p), 최종출력층은 m개의 뉴런을 갖는 것으로(yk, k=1,...,m) 설정하면
여기서 wkj, vji,는 연결강도를 나타내는 매개변수이며 bk, cj는 편차를 보정하는 매개변수이고 fy 및 fz는 활성화 함수이다. 즉 입력변수가 n개이고 출력변수가 m개인 신경망구조가 된다.
나온 결과값을 실제 값과 비교하여 그 차이를 최소화시키는 목적함수를 만들어 낼 수 있다.
여기서
일반적으로 활성화 함수 fy 및 fz는 sigmoid 함수나 tanh함수를 많이 사용해왔으나 최근에 딥러닝에 적절한 Relu함수를 개발하여 많이 사용되고 있다. Relu함수의 형태는
로 매우 단순한 형태이다. 결국 x가 음수를 갖게되면 0으로 처리하고 양수를 갖게 되면 x값을 그대로 선택하게 된다. 하지만 이런 단순한 형태를 통해 기존의 활성화 함수가 가지는 딥러닝에서 활성화 함수의 영향력이 층이 깊어질수록 감소하는 단점을 극복하고 비선형적요소를 가장 간단하게 나타낼 수 있어 딥러닝에서 가장 활발히 사용되고 있는 활성화 함수이다.
3. 최적화 알고리즘
일반적으로 매개변수 추정을 위한 최적화 알고리즘은 오차역전파(backpropagation)방법을 사용하는데 이는 초기에 매개변수를 무작위로 주고 목적함수가 작아지는 쪽을 찾아가면서 매개변수들을 갱신해 나가게 된다. 각각의 매개변수가 모두 1회 갱신되는 기간을 가중치조정주기(epoch)라고 부른다.
딥러닝은 여러 비선형 변환기법을 조합하여 복잡한 자료 속에서 핵심적인 내용의 요약을 시도하는 기계학습의 집합으로 정의된다. 딥러닝을 위해 기본적으로 인공신경망이 들어가게 되는데 매개변수를 보다 효과적으로 추정하기 위하여 최근에 여러 가지 알고리즘이 개발되었다. 본 연구에서는 다양한 매개변수 추정을 위한 최적화 알고리즘에 대해 수문자료를 이용하여 분석하였다.
특히 최근에 개발된 여러 방법들을 테스트하였다. 매개변수 추정 이론들은 최근에 개발이 이루어져서 방법들이 일반적인 저널에 실리기보다는 학회에서의 발표 또는 온라인 강좌 등에 알려져 현재 사용되고 있다. 이는 최근에 개발된 최적화 알고리즘이 수학적 검증의 전 단계에서도 실용적으로 유용할 경우 빠르게 사용되고 후에 그에 대한 검증이 이루어지고 있음을 보여준다. 수학적 이론들은 아래와 같다.
3.1 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
인공신경망 매개변수를 추정하는데 이제까지 가장 많이 사용되는 방식인 SGD법은 Eq. (3)에 나타난 목적함수(O)에 대해서 갱신할 매개변수의 집합 W으로 표현된다. Eq. (3)의
여기서 η는 학습률을 의미하며 0.01이나 0.001등의 값으로 미리 정해서 사용한다. 식에서 보는 바와 같이 확률적 경사 하강법은 가장 경사가 심한 방향으로 일정한 값(η)만을 이동하는 단순한 방법이다.
3.2 적응 경사법 (Adaptive Gradient, Adagrad)
Adagrad는 변수 갱신 시 각각의 변수마다 다른 학습률을 주는 것으로 이미 변화를 많이 한 변수들은 학습률을 작게 하고 변화가 많지 않았던 변수들은 학습률을 크게 하여 갱신해 나가게 된다(Duchi et al., 2011). 이는 적게 변화한 변수들이 최적화 값에 도달하기 위해서는 많이 이동해야할 확률이 높기 때문이다. 이를 식으로 나타내면 다음과 같다.
여기서 갱신의 크기는 기울기에 고정학습률와
Adagrad의 장점은 한번 학습률을 설정하면 자동적으로 학습률이 작아지면서 학습을 진행하게 된다. 하지만 단점은 학습률이 너무 작어져서 결국 거의 움직이지 못하는 단점이 있다. 이유는 ht가 계속해서 커지는 구조가 되기 때문이다.
3.3 RMSprop (Root Mean Squared propagation)
RMSProp은 Adagrad의 단점을 해결하기 위한 방법으로 ht를 합이 아니라 감소평균(decaying mean)을 이용하여 가중치를 주게 된다(Hinton, 2012). 이럴 경우 ht는 무한정 커지지 않으면서 과거의 기울기 정보를 서서히 잊고 새로운 기울기 정보를 크게 반영하게 된다. 이를 식으로 표현하면 다음과 같다.
여기서 ν는 기존영향을 감소시키는 계수로 0.999 같은 값을 사용하게 되며 ε은 ht가 극소로 작아져 0으로 가게 되는 것을 막아주는 값으로 보통 10-8을 사용하게 된다(Hinton, 2012).
ht가 Adagrad처럼 계속해서 커지는 구조적 단점을 보완하고 최근 변수간 학습률의 차이를 유지하게 된다.
3.4 Adaptive Delta (AdaDelta)
AdaDelta는 RMSprop과 유사하게 Adagrad의 단점을 보완하기 위한 것이다(Zeiler, 2012). 상수학습률η 대신 Newton’s second-order optimization과 같은 방식으로 변화값의 제곱을 이용하는 대신 Hessian 행렬을 사용한다. 대신 Hessian 행렬의 대각행렬만을 구하고 이를 지수감소 형태로 최대한 단순한 식을 만들어 내게 된다. 이는 다음과 같은 식으로 계산된다.
위의 식은 올바른 단위까지 고려하여 유도 되었다. AdaDelta의 경우 학습률의 초기값조차 줄 필요가 없다.
3.5 Adaptive Moments (Adam)
Adam 방법은 RMSprop과 Adagrad 방식을 혼합한 방식으로 1차 경사식(first-order gradient)만을 필요로 하고 매우 작은 메모리 기억만을 요구한다(Kingma and Ba, 2015). Adam의 주요 장점은 매개변수 갱신의 크기가 경사의 재스케일(rescaling)에 상관이 없으며 변화 폭은 대략 하이퍼매개변수(Hyperparameter)의 변화 크기에 제한된다는 것이다. 식은 다음과 같다.
여기서 μ는 이전의 매개변수 갱신값의 영향력을 감소시키는 계수이다. 여기서 1-μt와 1-νt는 값이 가지는 편차를 보정해주는 보정치이다. Adam은 모멘트 방법과 같이 공이 굴러내려오는 형태를 띄우나 그 공이 무거워 마찰을 가지는 형태가 되어 평평한 최소값들을 선호하는 형태가 된다. 방법의 개발자는 경험적으로 Adam이 여러 가지 상황에서 가장 적절한 방법임을 보였다(Kingma and Ba, 2015).
3.6 Nesterov-accelerated adaptive moment (Nadam)
Nadam 방법은 Nesterov’s accelerated gradient (NAG)와 RMSprop를 결합한 방식이다(Dozat, 2016). NAG는 다음과 같이 매개변수를 갱신하게 된다.
즉 mt-1은 현재의 경사도(
4. 자료 및 적용방법
본 연구에서는 Fig. 1에 보이는 남강댐유역에 대해서 강우량을 바탕으로 유출량을 추정하는 연구를 수행하였다. 남강댐유역의 크기는 2285km2이며 왼쪽의 남강유역(Fig. 1의 S1)과 오른쪽의 덕천강유역(Fig. 1의 S2)의 유량이 만나 하류에 위치한 남강댐으로 들어오게 된다.
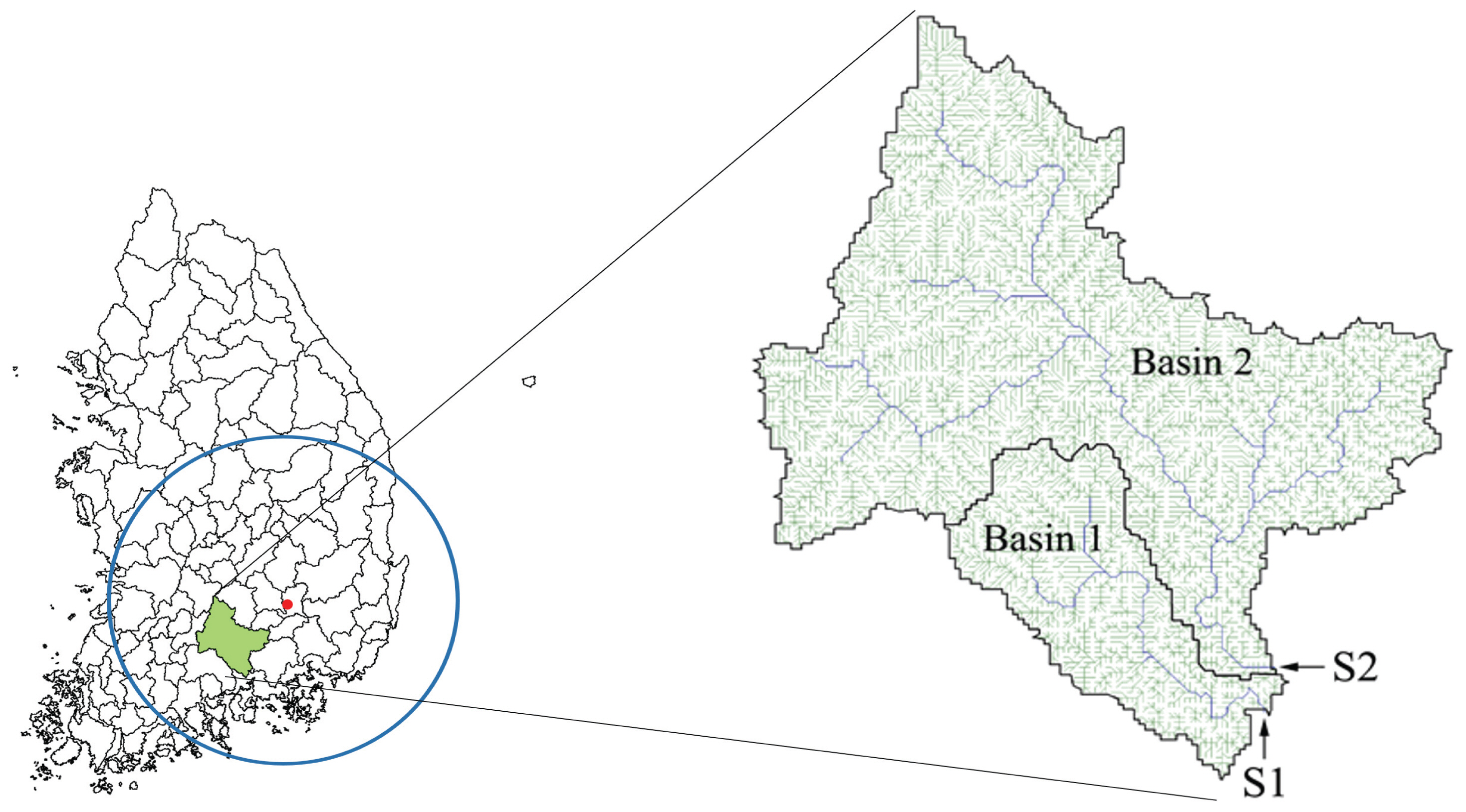
The Nam River Basin and the Outlfows from two Major Tributaries are Joined Together to Become the Total Inflow of Nam River
남강댐유역은 여름에 태풍 및 집중호우로 인하여 홍수가 자주 발생하는 지역이다. 또한 들어오는 유입량에 비해 댐 규모가 크지 않아 태풍 발생 시 선행적으로 수위를 낮추어 대비하고 홍수 발생 시 사천방향의 제수문으로 대부분의 유량을 방류함으로써 수자원이용과 치수에 매우 취약한 유역이다.
본 연구에서는 태풍 매미, 루사 등 한반도에 가장 큰 피해를 미쳤던 호우사상이 포함된 2001년에서 2004년간 주요 호우사상에 대해서 5개의 주요 강우관측지점인 창원, 임천, 진주, 지리산, 산청, 태수의 일강우량을 바탕으로 남강댐으로 들어오는 일유입량을 예측하였다.
남강댐 유입량 예측을 위해 사용된 입력 노드는 총 5개 지점의 일강우량이며 다양한 은닉노드 개수를 테스트하여 목적함수(Eq. (3))를 가장 작게 산정해주는 10개의 은닉 노드수가 가장 적합한 것으로 확인되어졌다. 최적화 기법마다 크게 다르지는 않아 모든 최적화 기법의 일률성을 위해 10개의 노드수를 기반으로 하였다.
활성화 함수는 앞서 설명에서 나왔던 바와 같이 현재 딥러닝에서 가장 많이 사용되고 있는 Relu함수를 바탕으로 테스트를 실시하였다.
인공신경망은 복잡한 모델과정이 포함되어 있어 그 불확실성도 상당히 크다. 따라서 본 연구에서는 각각의 최적화 알고리즘에 대해 매개변수 추정을 100회씩 반복 수행하였다.
또한 일반적으로 신경망 모델에서는 자료의 크기나 범위가 다르거나 클 경우 여러 문제점이 발생하므로 자료를 일정 범위로 변환하여 사용하였다. 본 연구에서는 먼저 모든 변수들을 정규화(normalization)한 후 값을 계산한 뒤 정규화복귀 (back-normalization)과정을 거쳤다.
5. 결 과
일반적으로 인공신경망을 통한 모델링은 자료를 훈련자료(Training), 테스트자료(Test), 검증자료(Validation) 세 부분으로 구분한다. 본 연구에서는 전체 자료에서 남강댐 일유출량 추정을 위해 30%를 검증 자료로 사용하고 나머지 자료 중에서 훈련자료를 80% 테스트자료를 20%로 사용하였다.
Fig. 2에는 전체 2500회의 가중치조정주기(epoch)에 따른 Eq. (3)의 손실함수를 테스트자료에 대해서 보여주고 있다. 가중치조정주기는 인공신경망의 매개변수를 회수를 의미한다. 일반적으로 손실함수는 가중치조정주기가 길어짐에 따라 훈련자료에 대해서는 초반에 급격하게 떨어지고 후반에는 거의 변화가 없는 것이 일반적이고 테스트 자료에 대해서는 초반에 급격히 떨어진 후 후반에 어느 시점이 되면 다시 상승하여 과적합(overfitting)이 그 부분에서 일어나게 됨을 알 수 있다.
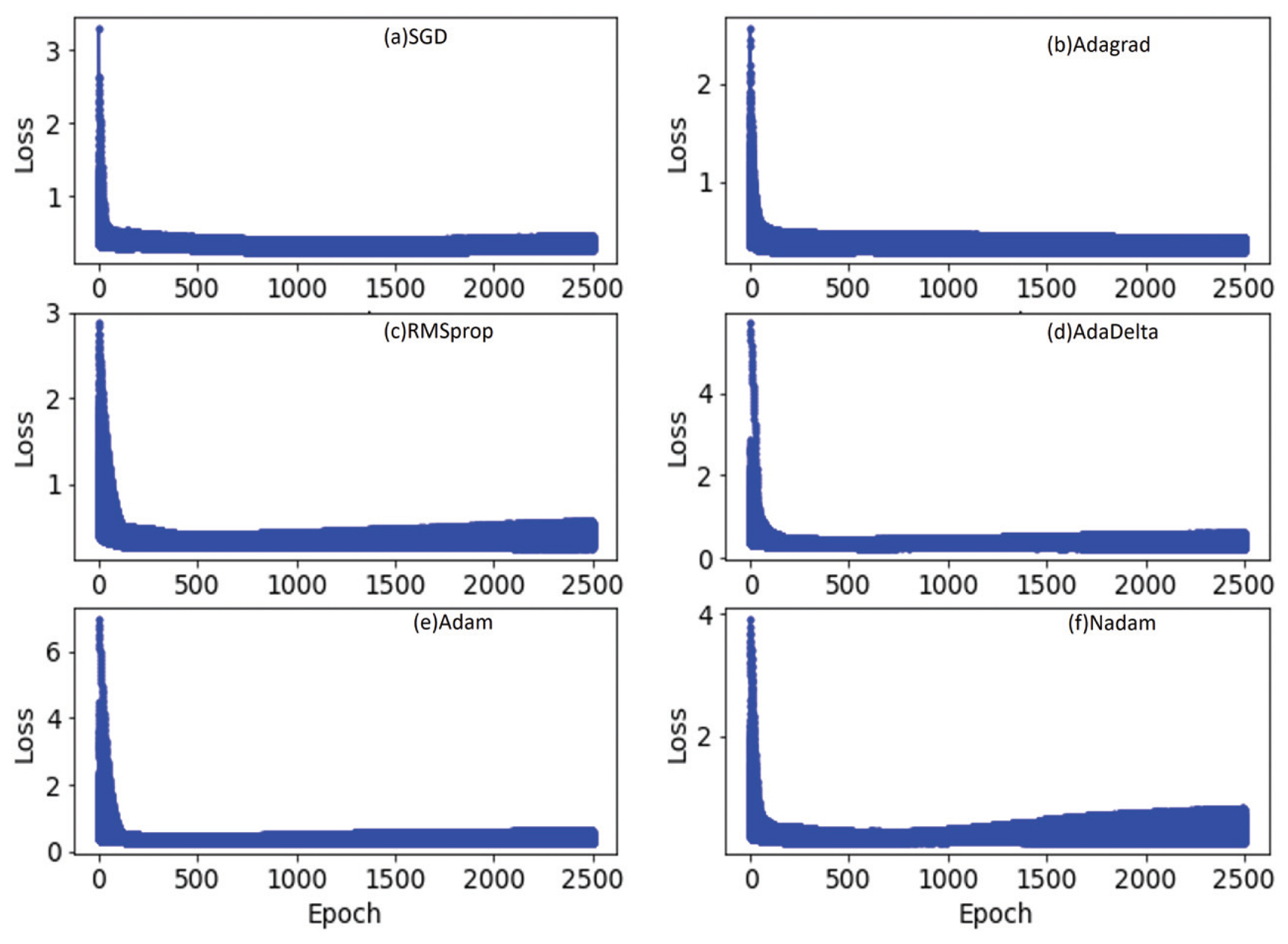
Loss Function as a Function of Epoch for the Testing Data with Fitting the Neural Network Model 100 Times at Each Optimization Algorithms
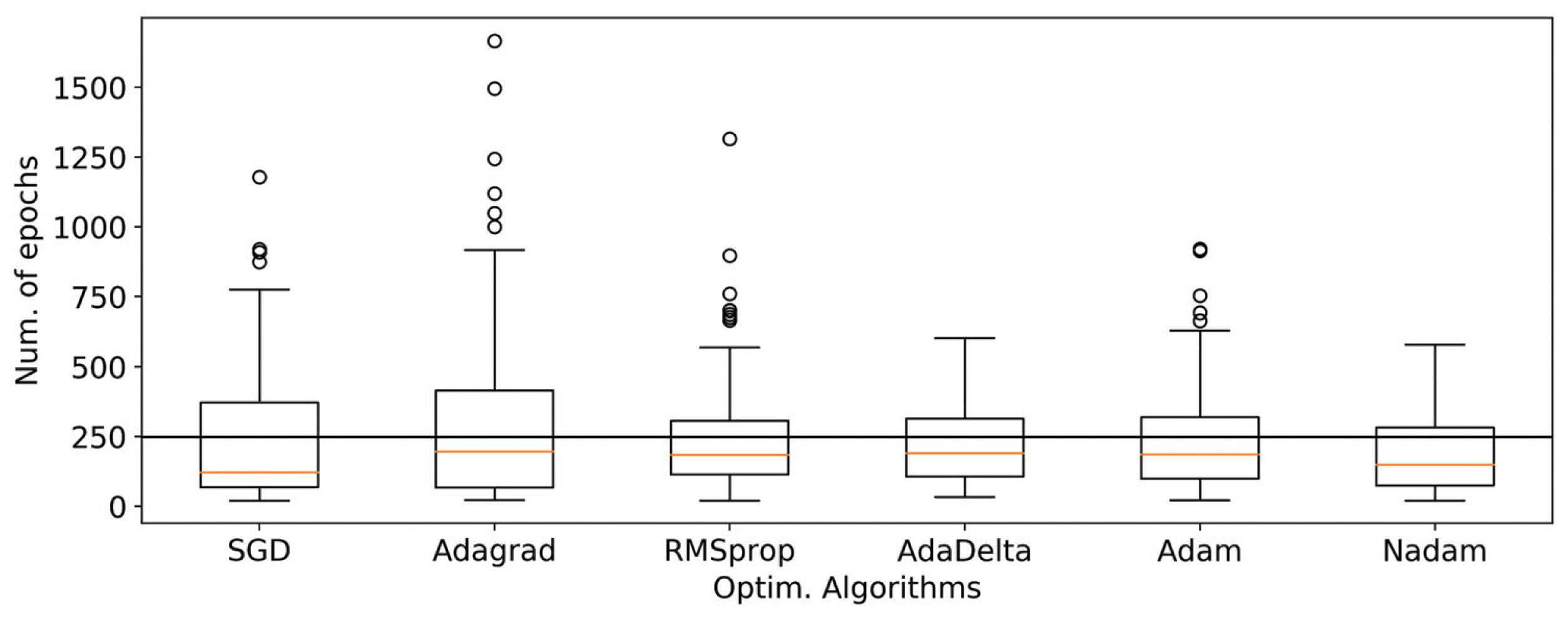
이러한 과적합이 시작되는 시점에서 가중치조정주기(epoch)를 중단하고 갱신된 매개변수를 적용하게 된다. Fig. 3에는 과적합 전에 중단된 가중치조정주기(epoch)의 수를 100회 실험한 결과치를 보여주고 있다. 가중치조정주기가 빠를수록 해당 최적화 알고리즘 값을 빨리 찾는 것을 보여주므로 최적화 알고리즘을 선택하는 하나의 기준으로도 볼 수 있다. Table 1의 마지막 열에는 100회 가중치조정주기(epoch)의 회수를 평균한 수치를 나타내고 있다. 전체적으로 200-300회 사이를 반복하게 됨을 알 수 있고 Nadam이 200이하로 가장 작은 가중치조정주기를 보여주고 있으며 AdaDelta가 다음으로 작은 값을 나타낸다. 전체적으로 최근에 개발된 최적화 알고리즘들이 상당히 작은 조정주기를 나타냄을 알 수 있다.
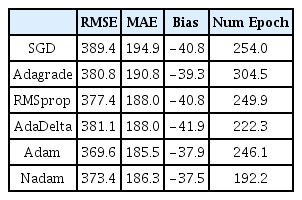
Average of Performance Measurment as RMSE, MAE, and Bias for Valdation Dataset with Different Algorithms in Neural Network as well as the Number of Epoch at the Last Column
특히 Nesterov’s accelerated gradient (NAG) 방법을 RMSprop와 결합한 Nadam방식이 다른 방법보다 빠르게 값을 찾는다는 것을 알 수 있었다.
인공신경망의 각각 최적화 알고리즘들을 통해서 구한 계산 일유출량들은 Fig. 4에 보이고 있다. 실제 값과의 차이를 정확히 보기 위해 다음의 3가지 방식으로 값을 비교하였다.
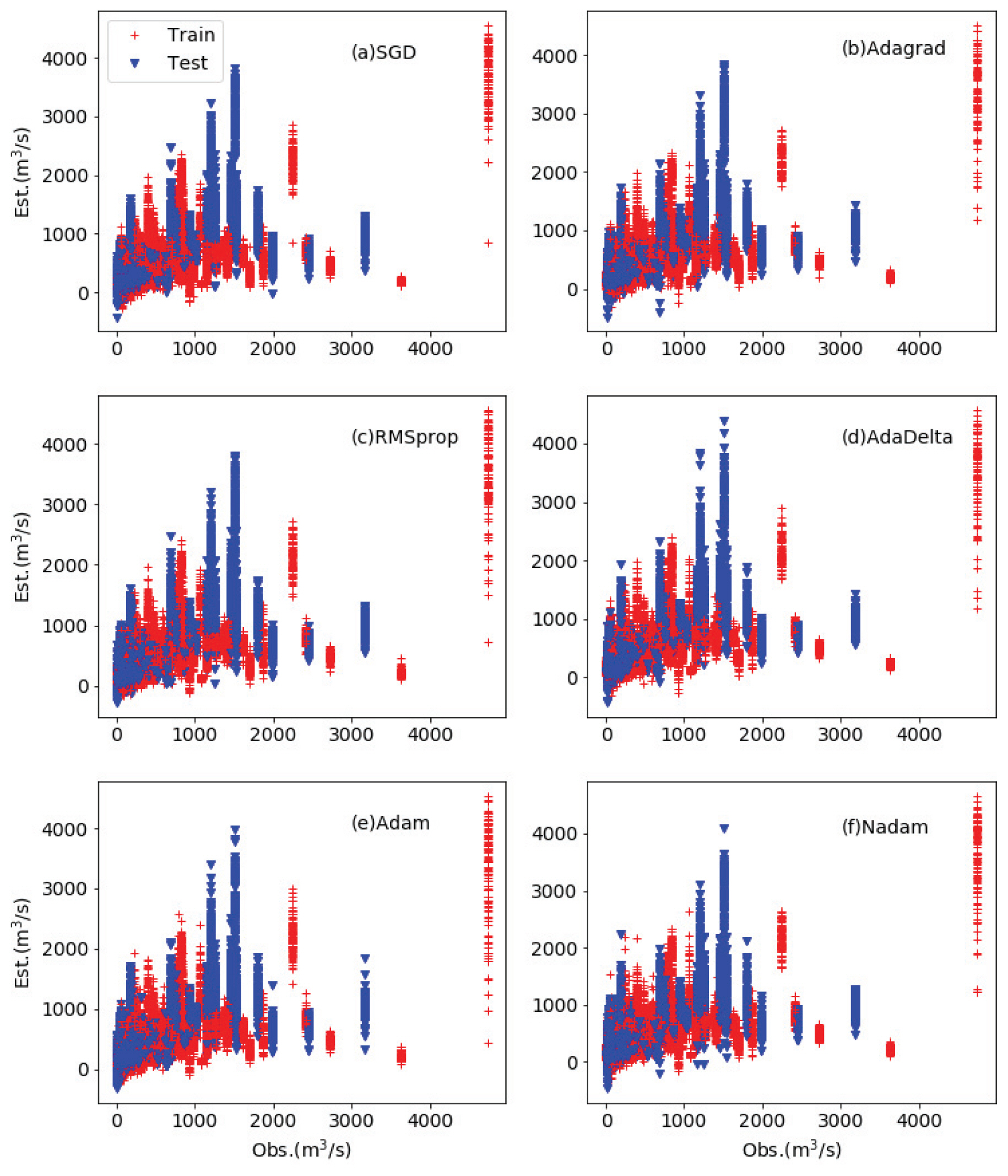
Observed (x-axis) Versus Estimated (y-axis) Streamflow (unit: m3/s) with Different Algorithms in Neural Network as Red + Marker (training and test data) and Blue Reversed Triangle Marker (validation data)
여기서
제시된 여섯 가지의 모든 최적화 알고리즘에 대해 100회씩 적용한 결과는 Fig. 5에 나타내었다. RMSE 및 MAE의 경우 Adam 및 Nadam이 가장 작고 SGD가 가장 크게 나타나는 것을 볼 수 있으며 이는 수치적으로 Table 1에 잘 나타나있다. Bias는 전체적으로 거의 비슷하게 음수를 가지는 것을 알 수 있는데 이러한 결과는 사용된 관측치가 강우 사상이 남강댐 지역데 최대가 되는 매미, 루사등의 태풍 사상에 대해서 모델링을 실시하여 나타나는 특징으로 극치값이 과소추정되는 강우유출모형의 일반적인 문제인 것으로 파악된다.

Performance Measurement as RMSE, MAE, and Bias for Valdation Dataset with Different Algorithms in Neural Network
최적화 알고리즘에 대한 결과를 전반적으로 비교해볼 때 큰 차이를 보이지는 않았으나 Adam 및 Nadam 방법이 최근에 소개되어온 방법 중 가장 적절한 방법임을 알 수 있다. Nadam의 경우 그 정확성에서는 Adam 방법보다는 조금 감소하는 부분이 있으나 매개변수들의 최적화 조정주기가 Adam보다 훨씬 짧게 나타남을 알 수 있었다.
6. 요약 및 결론
컴퓨터의 비약적인 발전으로 대량의 데이터나 자료들 속에서 여러 비선형변환기법을 통해 핵심적인 내용을 뽑아내는 기계학습의 집합체인 딥러닝에 대한 연구가 지속적으로 진행되어 오고 있다. 이를 위해 일반적으로 인공신경망이 사용되는데 인공신경망 안에는 많은 매개변수들이 포함되어 있고 이를 추정하기 위한 많은 최적화 알고리즘이 최근 개발되었다.
본 연구에서는 새로이 개발된 인공신경망의 매개변수들을 구하기 위한 다양한 최적화 알고리즘을 분석하고 특히 최근에 딥러닝을 위해 개발된 알고리즘에 대한 평가를 수문분야의 자료에 대해 분석하였다. 다지점 일강우량을 통한 일유출량을 계산해 내는 분야에 적용하였다.
결과를 통하여 분석된 여섯 가지의 최적화 알고리즘들이 큰 차이를 보이지는 않았으나 Adam 및 Nadam이 가장 적절한 매개변수 추정 알고리즘임을 확인할 수 있었고 기존의 SGD는 성능의 한계를 보였다. Adam은 그 성능자체는 가장 우수하나 Nadam보다는 최적화 가중치 조정주기(epoch)의 회수가 많이 필요한 것으로 밝혀졌다. Nadam의 경우 Adam보다는 성능이 조금 떨어지기는 하나 다른 방법들보다 훨씬 적은 조정주기를 거치는 것을 확인할 수 있다.
앞으로 본 연구에서 나온 결과를 바탕으로 매개변수 추정 알고리즘이 다양한 수문분야에 적용되어 일반화의 과정을 거친 다면 그 이용성이 증명되어 가는 딥러닝에 대한 수문학적 응용이 보다 용이해 질것으로 기대된다.
Acknowledgements
이 논문은 한국연구재단의 기초연구사업 지원을 받아 수행되었습니다(NRF-2018R1A2B6001799). 이에 감사드립니다. 본 연구는 경상대학교 연구년 연구교수 연구지원비로 수행되었으며 이에 감사드립니다.