통계적 접근을 통한 하천 횡단구조물 하부의 압력 변동성 및 수면 변위 특성 분석
Characteristic Analysis of Pressure Fluctuation and Free Surface Displacement in River-Crossing Structure through Statistical Approach
Article information
Abstract
돌발성 강우 등 기후변화로 인하여 보 하류 구조물의 안정성에 많은 문제가 발생하고 있다. 보 안정성에 영향을 끼치는 다양한 요인 중 도수로 인한 압력변동성도 주요 원인이 될 수 있다. 이에 본 연구에서는 보 상⋅하류 수심 비를 이용하여 다양한 흐름조건에서 도수로 인한 압력변동성 및 수면변위를 수리실험을 통하여 분석하였다. 이상치 제거 등 측정 자료의 신뢰성을 높인 후, 선행 연구를 통하여 도수 특성을 검토하였다. 상⋅하류 수심 비 및 Froude 수가 증가함에 따라 최대, 최소 압력의 크기가 증가하는 것을 확인하였고, 최대⋅최소 압력의 발생 위치는 일정 Froude 수 이상에서 각각 도수길이의 30%, 20% 지점에서 발생하였다. 또한, 상관분석을 통하여 압력 변동성과 수면 변동성이 강한 양의 관계를 갖는 것을 확인하였다. 향후 다양한 도수 발생 조건에서 압력 변동성과 수면변동성의 정량적인 관계를 도출해 낸다면, 보 하류 구조물 설계인자 도출에 기여할 수 있을 것으로 판단된다.
Trans Abstract
Abnormal climate change poses serious risks to the stability of river-crossing structures; these risks include piping, local bed scour and pressure fluctuation caused by hydraulic jumps. In this study, pressure fluctuation and free surface displacement were investigated by hydraulic experiments under various water depth ratios between the upstream and downstream sections of a weir. After removing outlier data by applying a statistical approach based on the confidence interval concept, the characteristics of a hydraulic jump were calculated from experimental results and compared to the results of previous studies. It was found that the maximum and minimum pressures increased with the water depth ratio and Froude number. In addition, above a certain Froude number, the maximum and minimum pressures occurred at 30% and 20% of the length of the hydraulic jump, respectively. The correlation analysis also indicated a strong positive relationship between the pressure fluctuation and the free surface fluctuation. Further quantification of this relationship under various hydraulic jump conditions would be useful for the design of the apron and bed protection.
1. 서 론
보 하류 구조물 중 물받이(Apron)는 도수(hydraulic jump)를 발생시켜 유수의 세력을 완화시킬 목적으로 설치한다. 따라서 물받이는 흐름에 안정성이 있는 구조로 설계하여야 하며, 본체를 월류하는 유수의 침식 작용 및 양압력에 견딜 수 있어야한다(Ministry of Land Infrastructure and Transport, 2016). 최근에는 이상기후로 인하여 집중호우의 발생 빈도 및 강우강도가 증가함에 따라 보 하류 구조물의 안정성에 문제가 발생하고 있다. 보 하류 구조물의 주요 파괴원인은 국부 세굴(bed scour), 파이핑(piping), 구조물 본체의 불안정 이며, 다양한 파괴 원인 중 구조물 본체의 불안정은 도수로 인한 압력변동성(pressure fluctuation)도 주요 원인이 될 수 있다. 이에 보 하류 구조물에서 도수로 인한 압력변동성에 대한 다양한 연구가 수행되었다. Ryu et al. (2017)은 수리실험을 통하여 도수로 인한 압력변동성을 고속카메라로 피에조메터를 촬영하여 시계열 분석을 수행하였다. 국외 연구로 Abdul Khader and Elango (1974)는 보 하류에서 도수로 인하여 발생하는 압력에 대하여 통계적 분석을 처음으로 수행하였으며, Toso and Bowers (1988)는 Froude 수 3 ~ 10 범위에서 다양한 수로 경사에 따라, 도수 발생 시 극한(extreme) 압력을 측정하였다. Fiorotto and Rinaldo (1992)는 수리실험을 통하여 도수발생 시 바닥에서의 압력을 측정하였고 압력변동성을 통계적 방법으로 분석하여 보 하류 구조물의 안정성이 압력변동성 성분에 의하여 영향을 받는다고 하였다. Bellin and Fiorotto (1995)는 도수발생 시 슬래브에 바닥에 작용하는 양력(uplift force)의 변동성을 실험을 통하여 검토하였으며, 설계 시 안전성을 고려한 압력계수(pressure coefficients)를 제시하였다. Armenio et al. (2000)은 Froude 수 6 ~ 9.5 범위에서 다양한 도수 형태에 따라 압력변동성을 검토하였으며, Güven et al. (2006)은 인공신경망(Artificial Neural Network)기법을 이용하여 도수 발생 시 발생 가능한 압력변동성 분포를 도출하였다. Kazemi et al. (2016)은 실험을 통하여 도수 발생 위치에서 압력변동성이 크게 발생하는 것을 확인하였고, 최대 유량 대비 0.47의 유량에서 압력변동성이 최대인 것을 확인하였다. 그러나 현재까지 대부분의 연구들은 Froude 수에 따라 도수 발생 시 압력변동성 현상을 확인하였으며, 측정된 압력데이터의 필터링 작업을 수행하지 않았다. 또한 다양한 상⋅하류 수심비로 인하여 발생하는 다양한 도수발생위치에 따른 압력변동성 검토에 관한 연구는 상대적으로 많지 않으며, 국내의 경우 도수로 인한 보 하부 구조물의 압력변동성 검토에 관한 연구가 매우 미비한 실정이다.
본 연구에서는 수리실험 상에서 측정되는 압력결과의 이상치 제거를 위하여 신뢰구간(confidence interval)을 적용하여 측정 압력데이터를 전처리(preprocessing) 하였고, 보 구조물 상⋅하류 수심 비에 따른 다양한 흐름조건에서 도수특성 및 압력변동성을 검토하였고, 추가적으로 초고속 카메라를 이용하여 도수 발생 시 수면변동성을 검토하여 압력변동성과 수면변동성 간의 상관관계를 확인하였다.
2. 기본이론
2.1 도수 발생 위치(location of hydraulic jump)
동일 흐름조건이라도 시간에 따라 도수의 위치가 변하기 때문에 도수 발생위치를 선정하는 것은 매우 어려운 일이다. Handbook of Hydraulics (Brater and King, 1976)에서는 유량 및 수면형을 알고 있다는 전제하에 도수 발생위치를 선정하는 방법을 제시하고 있다.
Fig. 1은 도수발생위치 선정방법 개념도이며, 공액수심(a′, b′, c′)과 하류수심의 연장선이 교차하는 점을 도수발생 위치로 선정하였다. 공액수심을 구하는 공식은 Eq. (1)과 같다.
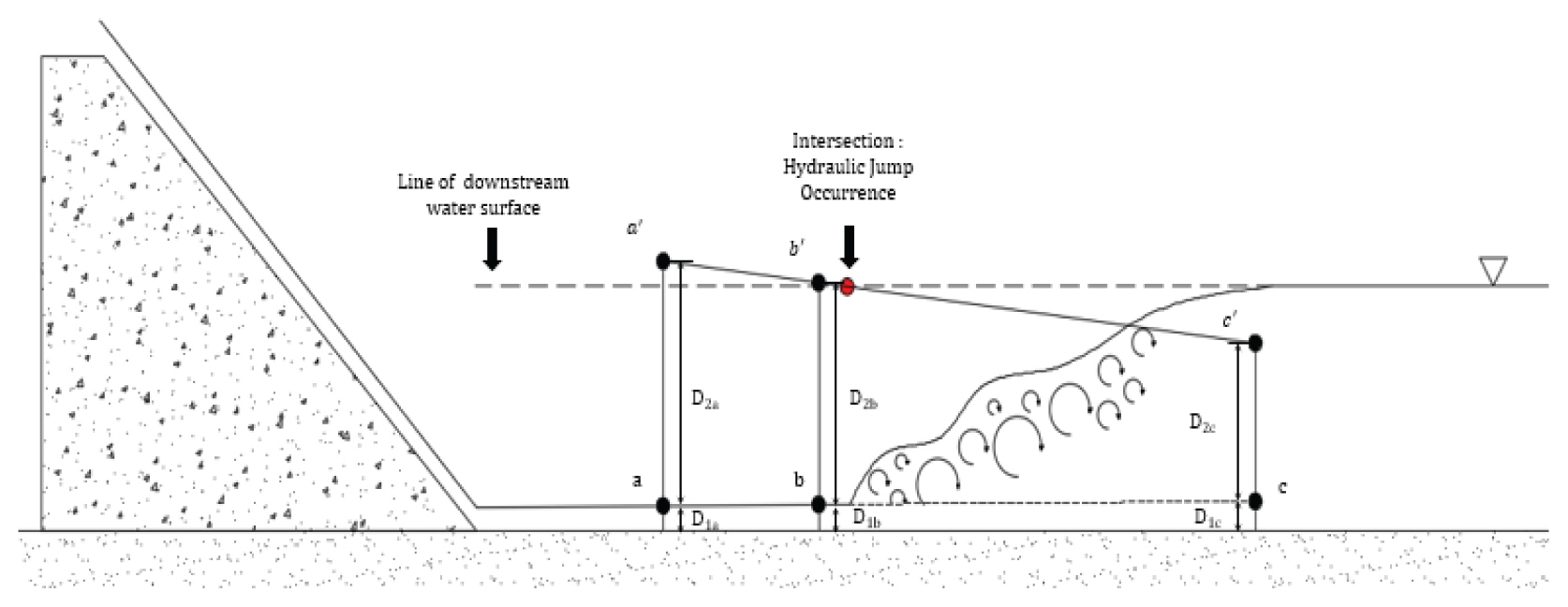
Position of Hydraulic Jump (Brater and King, 1976)
여기서, D1은 수심 (m), D2는 D1의 공액 수심 (m), V1은 D1지점에서의 유속 (m/s), g는 중력가속도 (m/s2)를 의미한다.
2.2 도수 길이 (hydraulic jump length)
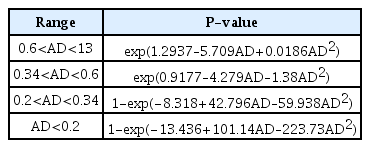
도수길이는 감세지(stilling basin)설계 시 중요한 인자로 가능한 모든 유량 조건에 대하여 도수가 감세지 내에서 일어나도록 해야 한다. 그러나 일반적으로 난류 흐름, 롤러(roller)와 와(eddy), 수면의 불규칙적인 교란 및 공기 유입 등으로 인하여 도수의 시작점과 끝점을 정확히 결정하는 것은 매우 복잡하다. 이에 선행연구에서는 다양한 도수 실험을 통하여 도수 길이를 Froude 수나 도수 발생 전 수심(h1) 및 도수 발생 후 수심(h2)으로 도출하는 공식을 제안하였다. Table 1은 선행연구에서 제안한 다양한 도수 산정 길이 공식을 제시하고 있다.
2.3 압력 변동성(pressure fluctuation)
압력 변동성은 평균 압력과 최대, 최소 압력의 차이를 의미하며, 압력 변동성은 물받이(apron)의 파괴와 직⋅간접적인 관련이 있기 때문에 물받이 설계 시 중요한 인자가 될 수 있다. 압력변동성은 Eq. (2)와 같이 표현할 수 있고, 특히 난류 흐름, 와, 수면의 불규칙적인 교란 등이 발생하는 도수 발생 시에는 최대⋅최소 압력을 검토하는 것이 필요할 수 있다. 일반적으로 압력 변동성은 무차원화 하여 계수로 표현하며, 다음 Eq. (3)은 최대⋅최소 압력에 대한 무차원화계수 산정식이다.
여기서, P는 불연속적인 압력(kPa),
2.4 수면 변동성 (free surface fluctuation)
도수가 발생하게 되면 압력변동성 외에도 수면변동성도 크게 나타난다. 수면 변동성은 에너지 소산(energy dissipation), 난류(turbulent), 와(eddy)와 관련이 있으며, Murzyn and Chanson (2009)에 의하면 수면 변동성은 난류 변동성(Turbulent fluctuation)으로 나타낼 수 있으며, 난류 변동성은 도수 상류 수심(h1)으로 무차원화 하여 다음 Eq. (4)와 같다.
여기서, C′TF 는 무차원화 한 난류변동성이며, η′은 수면변동성(m), η은 최대⋅최소 수심(m),
2.5 자료 전처리 및 통계분석(Data Preprocess and Statistical Analysis)
도수실험과 같이 변동성이 큰 실험 시 계측센서를 통하여 측정된 시계열 자료의 경우 이상치(outlier)가 발생할 수 있다. 자료 통계분석에서 이상치를 제거하기 위해서는 신뢰구간(confidence interval) 개념을 많이 사용하며, 신뢰구간은 정규분포와 표준편차(standard deviation, σ)를 이용하여 표현할 수 있으며, 신뢰구간에 포함되지 않은 자료는 이상치로 판단하여 제거한다. 또한 데이터의 분포 및 분포의 형태를 파악하기 위하여 왜도(skewness)와 첨도(kurtosis) 개념을 많이 사용한다(Kim, 2013).
왜도는 확률분포의 비대칭도를 나타내는 통계량을 의미하며 왜도가 양의 값을 가지면 우측으로 긴 꼬리를 갖은 형태, 음의 값을 가지면 좌측으로 긴 꼬리를 갖는 형태, 0이면 정규분포이다. 첨도는 확률분포의 뾰족한 정도를 나타내는 통계량을 의미하며, 첨도가 양의 값을 가지면 정규분포보다 뾰족하고, 음의 값을 가지면 정규분포보다 납작하고, 0이면 정규분포를 의미한다.
정규분포 여부를 판단하기 위하여 Anderson-Darling Equation (1954) 및 Kolmogorov-Smirnov Equation (1933)을 활용한다. Anderson-Darling 검정과 Kolmogorov-Smirnov 검정은 모두 데이터가 정규분포를 따른다는 가설(H0)과 데이터가 정규분포를 따르지 않는다는 가설(H1)을 이용하며 P-value 값이 0.05 또는 0.1 보다 작으면 데이터가 정규분포를 따르며, 0.05 또는 0.1보다 크면 정규분포를 따르지 않는다는 것을 의미한다. 각각의 공식은 Eqs. (7), (8)과 같다.
Anderson-Darling Equation (AD):
Kolmogorov-Smirnov Equation:
여기서, n은 총 표본수, Xi는 임의 데이터, F(Xi)는 정규분포의 누적분포함수를 의미하며, AD는 Anderson-Darling 공식의 통계량으로 AD값에 따라 P-value를 산정하는 식은 Table 2에 나타내었다.
두 변수 간의 관계를 파악하기 위해서는 상관 분석(Correlation Analysis)을 수행해야하며, 두 변수간의 관계의 강도를 상관관계(Correlation coefficient)로 나타낼 수 있다. 상관관계를 산정하는 방법은 일반적으로 Pearson 방법과 Spearman 방법을 사용하며 상관계수는 –1과 1 사이의 값을 갖게 된다. 상관계수가 –1에 가까우면 두 변수는 음의 선형관계를 가지고 1에 가까우면 두 변수는 양의 선형관계를 가지게 된다. 각각의 상관 계수를 구하는 공식은 Eqs, (9), (10)과 같다.
Pearson Correlation coefficient:
Spearman Correlation coefficient:
여기서, n은 총 표본수, σX, σY는 각각X, Y 변수의 표준편차,
본 연구에서 압력변동성을 파악하기 위해 계측된 시계열 자료인 압력자료는 100 Hz로 측정되어 한 경우에서 한 지점에서 평균 총 20,000개 이상의 데이터를 이용하였으며 신뢰구간 95%를 적용한 전처리 과정을 통해서 약 10%의 자료를 이상치(Outlier)로 판단하여 제거 후 실험결과 분석에 활용하였다.
3. 수리실험
3.1 실험수로 구축
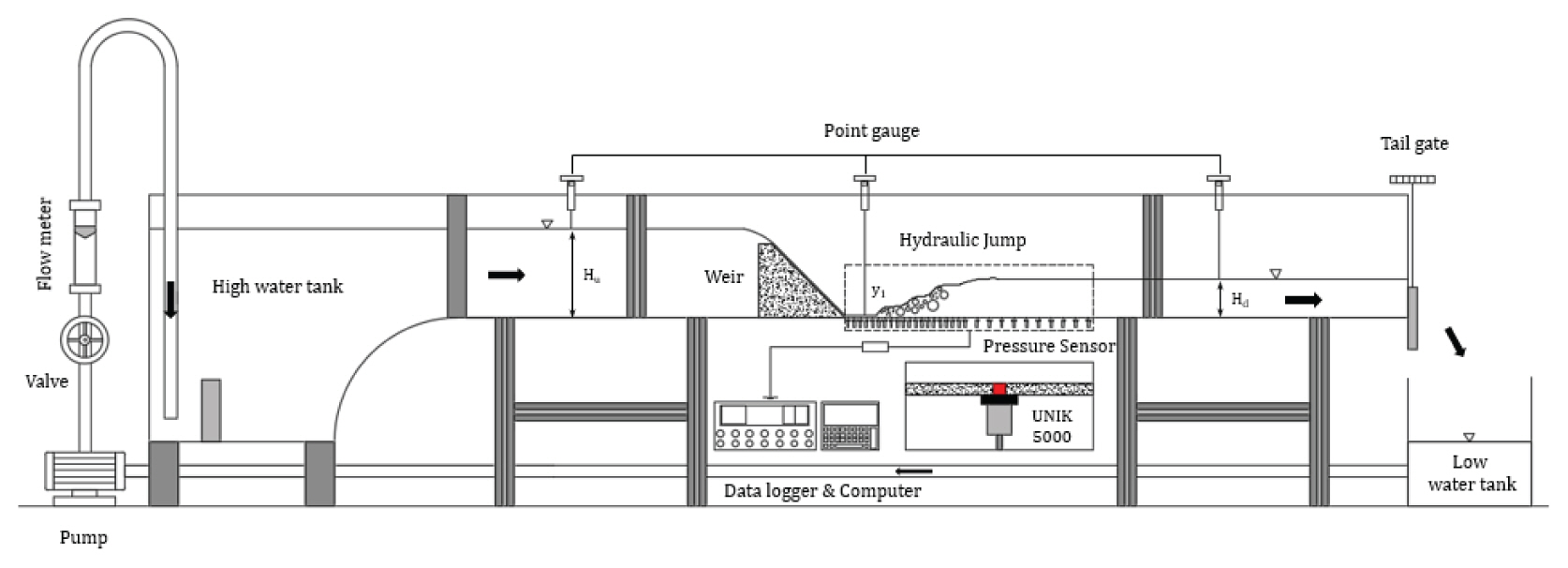
상⋅하류 수심비에 따라 발생되는 다양한 흐름조건 및 도수 발생위치에서 압력변동성 및 수면변동성을 수리실험을 통하여 검토하였다. 수리실험에 사용하는 수로는 직사각형 수로로 길이 10 m, 폭 0.3 m, 높이 0.4 m이며, 수로 바닥은 아크릴로 제작하였고, 수면변동성을 관측하기 위하여 측벽은 유리로 제작하였다. 상류 유입부로부터 2.5 m 떨어진 곳에 보(Weir)를 설치하였으며, 사다리꼴 형상(측면)으로 윗변 0.05 m, 아랫변 0.35 m, 높이는 0.3 m이다. 도수발생 위치에서 압력변동성을 검토하기 위하여 수로바닥에 지름 5 mm크기의 원형 구멍 총 30개소 중 보 구조물 끝단(toe)으로부터 20개소는 2.5 cm 간격으로, 10개소는 5.0 cm 간격으로 천공하였으며, 전압 방식 압력계(Model: UNIK 5000, Range: -2~5 kPa, Accuracy: ±0.04%)를 설치하였다. 본 압력계는 기존 연구(Carrillo et al., 2014)에서 유사한 규모의 개수로에서 압력측정에 사용된 것으로 측정 Frequency는 100 Hz로 총 200초간 측정하였다. 수면변동성을 검토하기 위하여 초고속 카메라(Model: Phantom Lab110 12G Mono Camera, 1028 × 1024 해상도, 초당 500 Hz)는 압력측정 위치로부터 1.0 m 떨어져서 설치하였다. 수로의 최대 유량은 25 m3/h로 펌프유량계를 사용하였으며 밸브를 이용하여 유량을 조절하였으며, 하류 수심은 Tail gate를 이용하여 조절하였다. 수심은 Point Gauge를 이용하여, 보 상류(Hu), 하류(Hd), 도수 발생 전(y1) 위치에서 측정하였으며 설치된 장비 및 실험수로 단면도는 Fig. 2에 나타내었다.
3.2 실험조건 및 수행
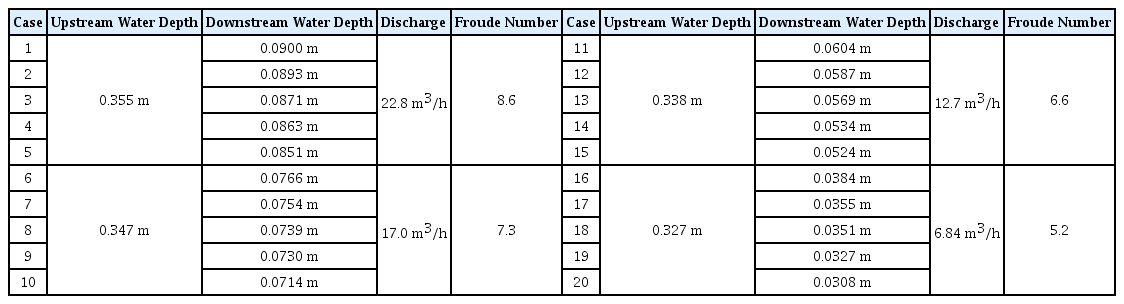
수리실험 수행 시 독립변수를 상⋅하류 수심으로 설정하였다. 보 상류 수심(Hu)은 유량계 밸브를 조절하여 최소 수심 0.327 m(유량: 6.84 m3/h)에서 최대 수심 0.355 m(유량: 22.8 m3/h)로 설정하였다. 보 상류 수심이 변화함에 따라 보 하류에 다양한 흐름조건을 발생시켰으며, Froude 수를 계산 하였을 때 범위는 5 < Froude Number < 9이다. 보 하류 수심(Hd)은 다양한 도수발생위치 재현 및 압력변동성 검토를 위하여 하류 Tail gate를 이용하여 조절하였다. 압력변동성을 측정하기 위하여 압력계의 Frequency는 선행연구(Fiorotto and Rinaldo, 1992; Bellin and Fiorotto, 1995)에서 50 Hz ~ 100 Hz로 측정하여 이를 참고하여 100 Hz로 설정하였으며, 필터링 기법을 적용하지 않고 총 200 초를 측정하였다. 수면변동성 검토를 위해서 초고속 카메라는 압력계의 측정간격(frequency)을 고려하여 동일하게 측정간격을 설정하여 도수현상을 속사(snapshot)로 촬영하였다. 실험조건은 다양한 Froude 수(Fr = 8.6, 7.3, 6.6, 5.2) 및 도수발생위치를 고려하여 총 20 Case로 설정하였으며 Table 3에 정리하였다.
4. 실험 결과 및 분석
4.1 도수 특성 분석
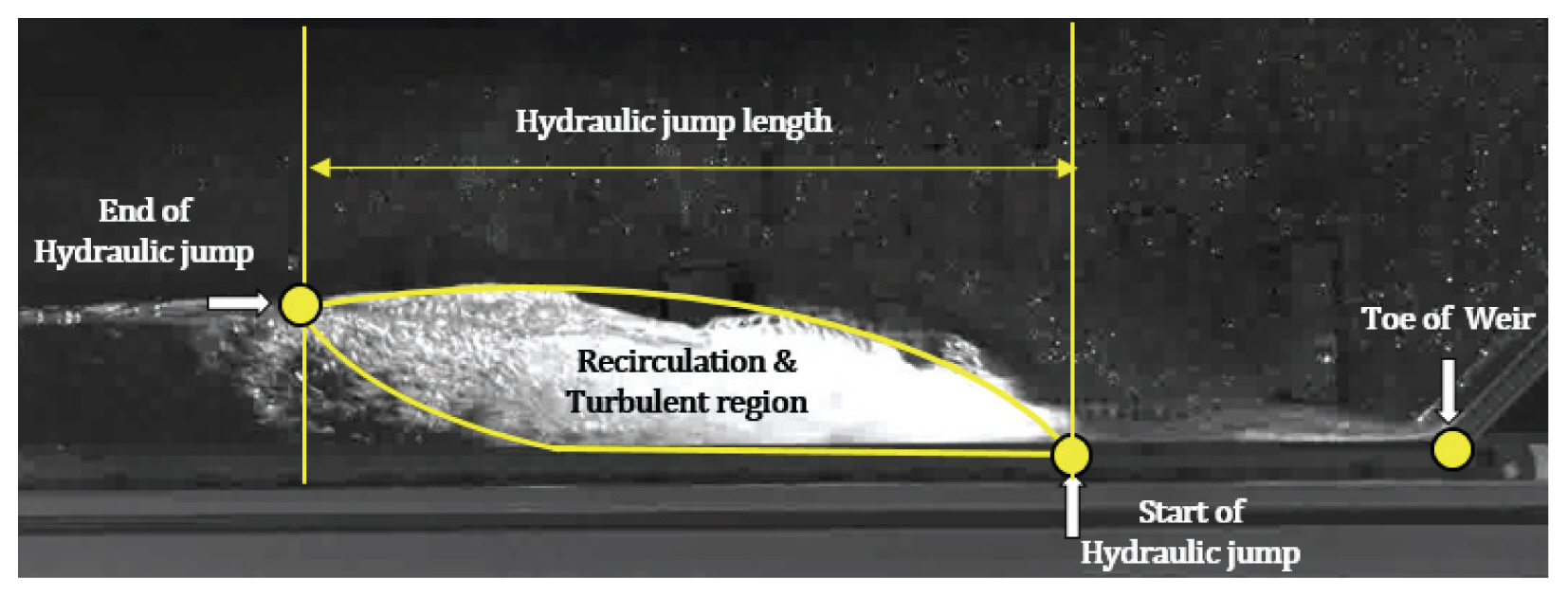
본 연구에서는 상⋅하류 수심비에 따라 발생되는 다양한 도수 특성을 확인하였다. 도수형태는 Froude 수가 5.2에서 8.6으로 안정도수(Stable Jump)이며, Case 별 도수 발생위치 및 도수길이를 검토하였다. 도수길이는 초고속 카메라로 촬영된 이미지를 이용하여 산정하였으며 각 이미지 별 산정된 도수길이 값을 평균하여 선행연구에서 제시한 여러 가지 도수길이 산정 공식과 비교하였다. 도수 발생위치 역시 촬영된 이미지를 이용하여 기존 도수발생위치 선정방법을 적용하여 선정하였다. Fig. 3은 이미지를 이용하여 도수길이를 산정한 방법이며, Fig. 4는 상⋅하류 수심비에 따른 선행연구의 도수길이 산정결과와 실험으로 산정한 도수길이를 비교하였다.
Fig. 4에서 Hd/Hu는 상⋅하류 수심비를 의미하며, Lj/Hw는 도수길이를 구조물 높이(Hw = 0.3 m constant)로 무차원화 하여나타내었다. 선행연구 도수길이 산정 식과 본 실험으로 산정한 도수길이는 비교적 일치하는 것을 확인하였으며 Froude 수가 증가함에 따라, 도수길이도 선형적으로 증가하는 것을 확인하였다. 반면, 동일 Froude 수에서 상⋅하류 수심비가 증가 할수록 도수길이는 선형적으로 감소하였다. 이는 도수 발생으로 인한 에너지 손실(Energy Loss)은 Froude 수가 증가함에 따라 증가하며, 동일 Froude 수에서는 상⋅하류 수심비가 증가함에 따라, 에너지 손실이 감소하기 때문이라고 판단된다. Fig. 5는 상⋅하류 수심비에 따른 도수 발생위치를 무차원화 한 결과이다.
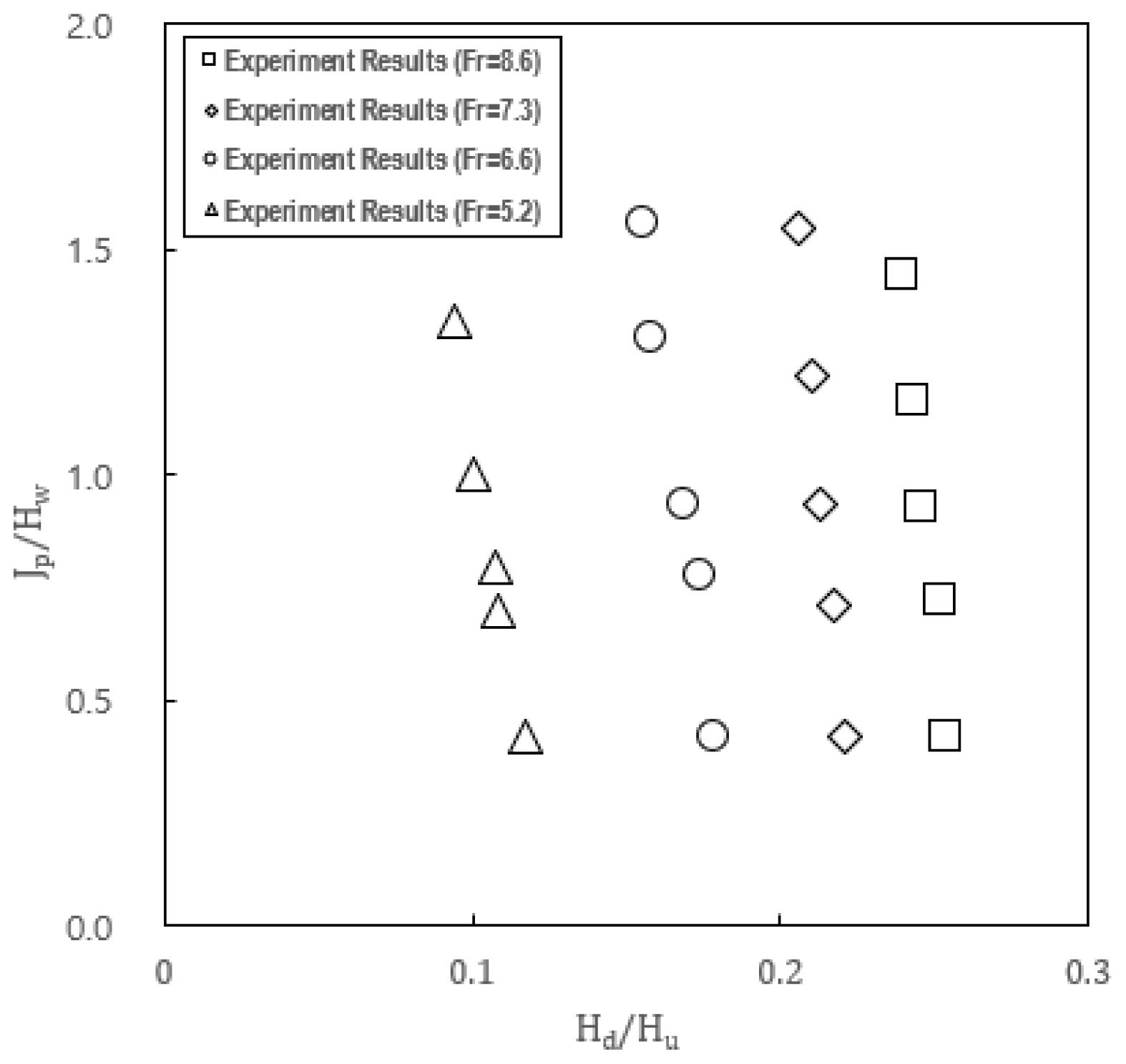
여기서, Hd/Hu는 상⋅하류 수심비를 의미하며, Jp/Hw는 보 구조물 끝단으로부터 도수발생지점까지의 거리를 구조물 높이(Hw = 0.3 m constant)로 무차원화 하여나타내었다. 도수발생 위치의 경우, 상⋅하류 수심비가 증가할수록 구조물 근처에서 발생하는 것을 확인하였다.
4.2 압력 변동성 결과 분석
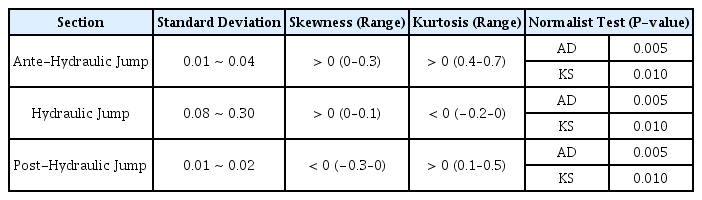
각 측점 별 측정한 압력 데이터는 신뢰구간 99.7% (μ±3σ) 개념을 적용하여, 총 20,000 개의 데이터 중 약 100개를 이상치(Outlier) 데이터라 판단하여 제거하였다. 각 Case에 따라 측점별 필터링 된 압력 데이터의 분포 및 특성을 검토하기 위하여, 도수 발생 전, 도수, 도수 끝난 후 구간으로 나누어 표준편차(Standard Deviation), 왜도(Skewness), 첨도(Kurtosis)와 Anderson-Darling 통계량(A2) 및 Kolmogorov-Smirnov 공식을 이용하여 정규성 검정을 수행하여 Table 4에 나타내었다.
세 구간 모두 P-value가 0.05 미만으로 정규분포를 따르지 않는 것으로 확인되었다. 특히 도수 구간에서는 표준 편차가 다른 구간에 비하여 크고, 첨도 값이 음수 값을 가진다는 것을 통하여 압력 변동성이 크다는 것을 확인할 수 있다. 상⋅하류 수심비 및 Froude 수에 따라 측점 별 압력변동성을 검토하였으며. Fig. 6은 각 Case에 대하여 압력 측점 별 평균 압력 및 최대⋅최소 압력을 무차원화 하여 압력계수를 나타낸 결과이다.
Fig. 6에서
Froude 수가 증가함에 따라, 무차원화 된 최대⋅최소 압력 발생위치는 선형적으로 감소하다가 Froude 수 7.3 이상에서 도수 발생 시작위치를 기준으로 최대 압력은 도수길이의 30% 지점, 최소 압력은 도수길이의 20% 지점에서 수렴하는 특징을 보였다.
4.3 수변 변동성 결과 분석
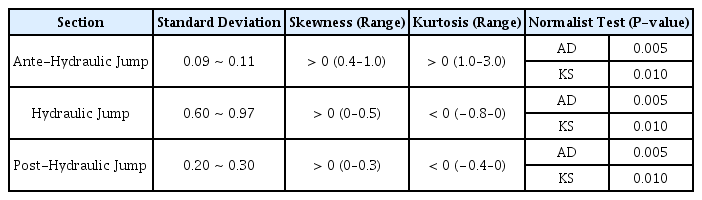
선행연구에 따르면 난류 변동성(Turbulent fluctuation)은 수면 변동성으로 표현을 할 수 있으며, 압력변동성이 난류 변동성과 연관이 있다고 판단하여, Case 1~5에 대하여 초고속 카메라로 촬영한 이미지를 이용하여 압력 측정 위치 별 시간 평균 최대 수심 및 최소 수심을 산정하였다. 수면 변동성도 압력변동성과 동일하게 도수 발생 전, 도수, 도수 끝난 후 구간으로 나누어 표준편차, 왜도, 첨도 및 정규성 검정을 수행하여 Table 5에 나타내었다.
수면 변동 데이터도 압력 데이터와 동일하게 세 구간에서 P-value가 0.05보다 작으면서 정규분포를 따르지 않는 것을 확인하였고, 도수 구간에서 표준편차가 다른 구간에 비하여 크고 첨도 값이 음수여서 변동성이 크다고 판단하였다. 하지만 압력 측정 자료와 달리, 도수가 끝난 후 구간에서도 수면변동성이 크다는 것을 확인하였다. Case 1~5에 대하여 수면 측정 자료를 활용하여 보 구조물 끝단으로부터 떨어진 거리에 따라 난류 변동성을 산정한 결과는 Fig. 9에 나타내었다.
여기서, η′/d1은 난류 변동성을 의미하며, H1과 H2지점은 압력 변동성으로 검토한 최소 최대 압력발생 지점이다. 난류 변동성 분석 결과, 도수 시작 지점에서 난류 변동성이 급격하게 증가하는 것을 확인하였고, 최대 최소 압력 발생지점에서도 난류 변동성이 비교적 크게 나타는 것을 확인하였다. 하지만 최대 최소 압력 발생지점과 최대 난류 변동성 발생지점은 다소 차이가 있다는 것을 확인하였다.
4.4 압력 변동성과 수면 변동성 상관 분석
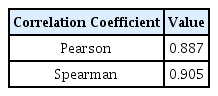
압력 변동성과 수면 변동성간의 관련성을 확인하기 위하여, 상관 분석(Correlation Analysis)을 수행하였다. Fig. 10은 수면 변동성에 따른 압력 변동성을 나타낸 그래프 이며 Pearson 상관 계수와, Spearman 상관계수를 계산하여 Table 6에 나타냈다.
여기서,
Pearson 상관계수 및 Spearman 상관계수 값은 각각 0.887과 0.905로 압력 변동성과 수면 변동성은 강한 양의 관계를 갖으며, 수면 변동성이 클수록 압력 변동성도 커진다는 것을 확인하였다.
5. 결 론
본 연구에서는 보 구조물 하류에서 도수 발생 시 압력 변동성 및 수면 변동성을 분석하기 위하여 수리실험을 수행하였다. 실험은 보 구조물 상⋅하류 수심을 변경하여 다양한 흐름조건에서 수행하였으며, 측정한 압력데이터는 통계적 접근으로 신뢰구간 개념을 적용하여 이상치(outlier)를 제거하였다. 필터링 된 압력데이터는 도수발생 전, 도수구간, 도수가 끝난 후 구간으로 나누어 분포를 검토하였으며 도수구간에서 변동성이 크다는 것을 확인하였다. 실험을 통하여 산정한 상⋅하류 수심비에 따른 도수 길이를 선행연구에서 제시한 도수길이 공식과 비교하여 일치한다는 것을 확인하였다. 또한 압력 변동성은 Froude 수 및 상⋅하류 수심비가 증가함에 따라 최대⋅최소 압력 크기가 증가하였으며, 최대⋅최소 압력 발생위치는 일정 Froude 수 이상에서는 각각 도수길이의 30%, 20%지점에서 발생하는 것으로 나타났다. 이는 해당 지점에서 난류(turbulent) 및 와(eddy)로 인하여 난류 변동성이 비교적 크게 발생하기 때문이라 판단되며 상관 분석을 통하여 압력 변동성과 수면 변동성은 양의 관계를 갖는다는 것을 확인하였다. 따라서 최대⋅최소 압력 발생 및 최대 압력변동성은 현재 하천의 보 구조물 하류에서 발생하고 있는 본체 불안정으로 인한 파괴의 주요 원인이 될 수 있으므로, 이에 대한 영향을 반영한 구조물 설계가 수행되어야 한다. 다만 본 연구는 모형실험이 아니며, 압력 변동성과 수면 변동성간의 정략적인 관계가 도출되지 않았기 때문에, 분석결과가 실제 하천의 보 하류 구조물 설계 시 유의미한 값이 되지 않는다고 생각한다. 이에 향후에는 보다 다양한 Froude 수 변화에 따른 도수의 다양한 종류를 재현하고 압력 변동성과 수면 변동성 외에도 유속 변동성을 분석하여 정량적인 관계를 도출해 낸다면 물받이공 길이, 두께 등 보 하류 구조물 설계인자 도출에 기여할 수 있다고 판단된다.
Acknowledgements
본 연구는 국토교통부 국토교통기술촉진사업 연구개발사업의 연구비지원(18CTAP-C133019-02)에 의해 수행되었습니다. 이에 감사드립니다.