네트워크 관점에서의 도시 우수관망 특성 분석
A Study on the Characteristics of Urban Storm Sewer Networks from a Network Perspective
Article information
Abstract
도시유역의 불투수층에 내린 강우는 대부분 지표면을 따라 흘러 우수관으로 유입되어 유역에서 배출된다. 그러므로 우수관의 적절한 설계와 우수관망의 특성을 이해하는 것은 도시 홍수 저감에서 가장 우선적으로 고려되어야 한다. 본 연구에서는 도시지역에서의 일반적인 관망의 형상을 갖추고 있는 유역을 대상으로 선정하였다. 도시 우수관망을 자연하천과 같이 복잡한 네트워크의 특성을 지닌 관망이라고 가정 하에 기존의 자연하천의 수계망에서 적용되는 개념들을 이용하여 적용하였다. 자연유역에 수계망에서 적용되는 Horton의 법칙을 이용하여 분기비 및 길이비를 산정하였고, 일부 대상유역은 수계망의 일반적인 범위를 만족하는 것을 확인하였다. 추후 본 연구에서 적용하였던 기존 이론 외에 다른 이론을 적용한 연구가 필요할 것으로 판단되며, 향후 도시 유역의 우수관 설계 시 우수관의 특성에 대한 기준도 제시한다면 보다 효과적인 우수관 설계와 도시 홍수 저감이 가능할 것으로 보인다.
Trans Abstract
Most of the rainfall over impervious surfaces of urban areas flows along the surface of the ground, flows into the storm sewer network, and is discharged from the catchment. Therefore, the proper design of storm sewer networks and understanding of the characteristics of storm sewer networks should be considered first in reducing urban flooding. In this study, we selected watersheds with a general sewer network in urban areas. It was assumed that the sewer network was a storm sewer network with the characteristics of a complex network, such as a natural stream. The concepts applied in natural stream systems were applied to the target watersheds. The laws of stream numbers and stream lengths were calculated using Horton's law, which is applied to the stream pattern of natural streams. It was deemed necessary to study the application of a different theory in addition to the existing theory that was applied in this study in the future. If the criteria for the characteristics of rainwater pipes are also presented in the design of rainwater pipes in urban areas, then more effective water duct design and urban flood reduction will be possible.
1. 서 론
현재 우리나라를 포함한 전 지구는 지구온난화로 인해 평균기온이 상승하고 있으며, 지역에 따라서는 강우강도와 강우량 또한 증가하고 있다. 우리나라의 강수량은 계절적 편차가 크고 여름철에 강우가 집중되기 때문에 기후변화에 의한 주기적인 홍수와 같은 자연재해로 인적, 물적 피해가 증가하고 있다. 도시화 및 산업화로 인한 불투수 지역의 증가는 하천으로 유입되는 첨두 유량의 증가, 도달시간의 감소 등 유역에서의 유출 특성을 변화시켜 홍수에 대한 방어능력을 취약하게 만들었다.
도시의 불투수지역에 내린 강우는 우수관을 통하여 유역에서 배출된다. 최근 들어 짧은 시간에 큰 강우강도를 갖는 호우의 발생빈도가 높아지고 있으며, 이러한 형태의 호우는 갑작스럽게 유출량을 증가시켜 우수관으로 유입되지 못하고 도시 지역에 국지적인 침수를 유발한다. 그러므로 도시의 내수침수 위험을 최소화하기 위해 우수관망의 적절한 설계가 매우 중요하다. Weng and Liaw (2005)은 유전자 알고리즘을 이용하여 맨홀과 맨홀 사이의 노선방향을 결정하고 결정된 연결 노선에 해당하는 최소비용의 최적설계 모형을 개발하였다. Kim et al. (2009)은 우수관망을 구성함에 있어서 관거 내 흐름을 분산시키고 제어하기 위하여 맨홀간 관거의 연결 방향을 조정함으로써 관내 유입량을 분산시키고 그 결과 유출구에서의 첨두 유출량을 저감하였다. Lee (2010)은 유전자알고리즘을 이용하여 노선결정을 통한 우수관망의 유출부에 첨두유출량을 최소화 하였고, Sun et al. (2011)은 최적화 과정을 통한 건설 비용과 홍수 위험 비용을 포함한 전체 비용과 관련하여 최적의 설계모형을 제시하였다. Lee (2012)은 다목적 최적화 기법을 이용한 도시유역 경계 결정 및 내수침수 위험을 감소시키기 위하여 유출구의 첨두유출량을 최소화하는 유역의 경계를 설정하고 우수관망을 설계하는 최적설계모형을 개발하였다. 유전자 알고리즘은 이용한 연구사례로 Kwon et al. (2018)은 도시 내배수시스템에 탄력성의 개념을 고려하고 최적화기법인 화음탐색법(Harmony Search Algorithm, HAS)를 사용하여 관거의 노선 및 제원을 동시에 결정할 수 있는 탄력성-제약조건을 기반으로 다양한 수준의 침수피해 심도를 제약조건으로 고려하여 최적화를 수행하였다. 또한 도시 유역의 우수관망 통수능 LID 기술 적용 연구로 Baek. et al. (2017)은 합리식에 의해 계획된 도시유역의 우수관망이 단기간에 집중된 강우와 지형학적 요인으로 통수가 원활하지 않을 경우에 LID 기술 도입의 효과로 안전한 우수관망 시스템설계가 가능한지와 적정성에 대한 연구를 수행하였다.
우수관망의 증설 시 우수관망의 적절한 위치와 설계 등을 위하여 우선적으로 연결구조 특성을 파악하고 관망 내 흐름을 이해하는 것이 수행되어야 한다. 이러한 우수관로의 설계 시 치수목적을 고려한 설계방법에 주안점을 준 연구는 많이 진행되어 왔지만, 우수관망을 네트워크(Network)의 관점에서 바라보고 그 특성을 이해하고자 하는 연구는 미흡한 실정이다. 수자원 분야에서의 네트워크 시스템은 자연하천에서 수계망으로 볼 수 있다. 수계망은 두 개 이상의 점 사이에 경로로 이루어진 복잡한 네트워크이다. 수계망의 특성에 관한 연구로는 Horton (1945)과 Strahler (1957)은 자연하천이 나뭇가지 모양으로 갈라져있는 정도를 정량적 방법으로 나타내는 하천차수의 법칙을 고안하였다. 또한 Horton (1945)는 반대수지상에서 유역에서의 하천차수와 각 하천차수의 개수와 하천차수의 평균길이가 서로 선형의 관계를 가지고 있다는 것을 발견하였다. 시간의 경과에 따라 스스로 구성되는 자연하천의 수계망과 같이 우수관망의 설계는 도시의 형성에 따라 계획적으로 이루어지지만, 도시의 발전으로 인한 도로 및 건물의 증가로 인한 관망의 확장이 이루어지면서 시간이 지나면서 스스로 형성되는 네트워크라고 할 수 있다. 따라서 우수관망은 하나의 인공적인 수계망이라고 할 수 있다.
본 연구에서는 우수관망의 증설 시 추가되는 우수관망의 적절한 위치선정 등을 고려하기 위하여 우수관망을 네트워크 관점에서 연결구조의 특성을 분석하였다. 우수관망을 하나의 수계망이라는 가정 하에 자연하천의 수계망에서 제시된 법칙들을 적용함으로서 수계망과 도시 우수관망의 네트워크 연결구조 특성의 상관성을 분석하고 이해하고자 한다.
2. 분석 방법
2.1 Horton의 법칙
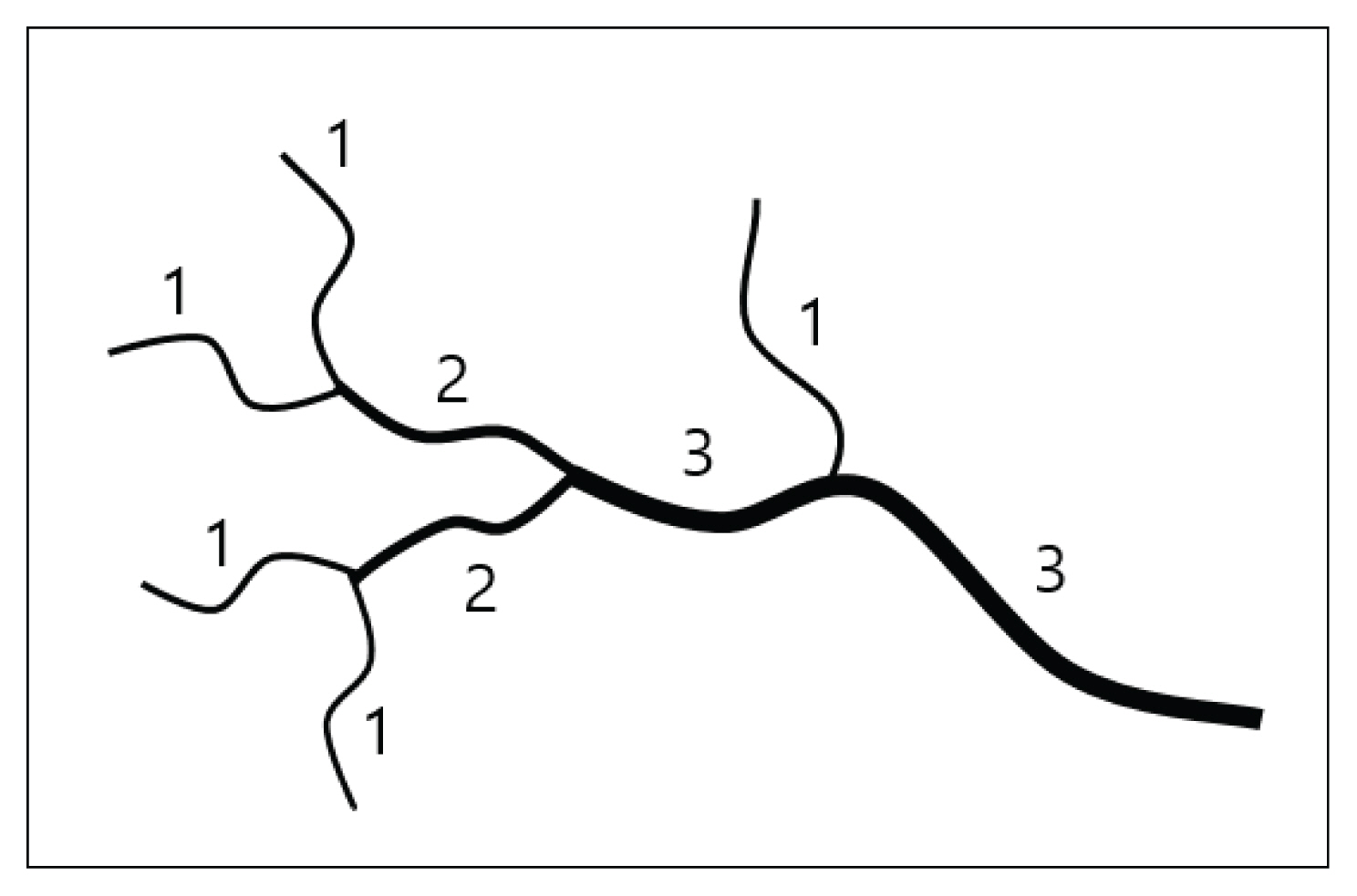
하천차수의 결정은 Horton (1945)의 일반적으로 자연하천 유역의 구성과 하도망의 형태에 관한 정량적인 연구로 시작되었다. 하천의 나뭇가지 형태의 수계망을 정량적으로 나타내기 위하여 차수법칙을 제시하였다. 그 후 Strahler (1957)는 Horton의 차수법칙을 수정하여 체계화시켰다. Fig. 1과 같이 더 이상 분기되지 않는 유원에서 시작하는 하천을 1차 하천으로 하고, 같은 차수의 하천이 만나서 합류되면 차수가 증가하고 차수가 서로 다를 경우는 차수가 높은 하천의 차수를 유지하는 하천차수 결정방법이다.
Horton – Strahler Law
이를 이용하여, Horton (1945)은 수계망에서 하천차수와 각 하천차수의 개수, 하천차수와 평균길이가 반대수지상에서 서로 선형의 연관성을 가지고 있다는 것을 발견하였다. 또한 유역내에 차수가 동일한 하천의 개수를 다음과 같이 나타내었다.
여기서, i는 하천의 차수이며, Ni는 i차 하천의 개수이며, Ω는 유역의 최고차수이다. RB는 하천의 분기비로서, 하천 차수별 하천의 개수를 산정하고 각각에 대수를 취하여 구한 직선의 기울기는 logRB로 나타낸다. Lij는 i 차의 하천 길이이며, Aij는 i차 하천의 유출에 기여하는 면적이다.
유역내에서 임의의 차수에 대한 하천의 평균길이(
또한, 분기비(RB), 길이비(RL), 면적비(RA)를 다음과 같이 정의하였다.
일반적인 자연하천유역의 수계망에서는 분기비가 3.0~5.0의 값을 가지고 있으며, 길이비는 1.5~3.5, 면적비는 3.0~6.0의 값을 갖는다. 특히 분기비의 경우 이론적인 최소값은 2.0이나 자연하천 유역에서는 거의 나타나지 않는다.
3. 대상유역 선정 및 우수관망 특성
3.1 대상유역 선정
본 연구에서는 인구와 건물이 밀집되어 있고 도시지역에서의 일반적인 관망의 형상을 갖추고 있는 유역을 대상으로 선정하였다. 대상 유역으로 목감천유역에 위치한 개봉1, 2빗물펌프장 유역(A)과 도림천유역의 신림1, 2동 빗물펌프장 유역(B)과 신림5동 빗물펌프장 유역(C)을 선정하였다.
지방 하천인 목감천 유역의 빗물펌프장이 존재하여, 각각 개봉1, 2 빗물펌프장이다. 본 연구에서 사용한 목감천 유역 중 서울시 구간의 면적 8.92 km2은 개봉2 빗물펌프장이 안양천으로 배제시키고 있다. 설계빈도는 개봉 1동 빗물펌프장은 5년 빈도이며 저수용량은 156,000 m3이고 개봉 2동 빗물펌프장은 10년 빈도이며 저수용량은 3,460 m3이다. 개봉1, 2 빗물펌프장의 배수유역이 포함되어있는 구로구의 경우 총 면적 2,011 ha 중 대지가 39.44%인 7.93 km2으로 가장 높은 비율을 차지하고 있으며, 임야가 3.87 km2으로 19.25%로 두 번째로 높은 비율을 차지하고 있다. 광명시 토지의 총면적 385.1 km2 중 임야가 14.53 km2, 37.73%로 가장 높은 비율을 보이고 있으며, 시흥시 또한 총면적 134.52 km2 중 임야가 40.75 km2, 30.29%로 가장 높은 비율로 조사되었다(Jang, 2009). 목감천의 우수관망은 Fig. 2에서 알 수 있는 것과 같이 대부분 수지상형으로 구성되어 있다.
Study Catchments and Respective Storm Sewer Networks
도림천유역은 서울 관악구 신림동에 위치하고 있으며 신림1동 빗물펌프장과 신림2동 빗물펌프장이 위치하고 있다. 신림1동 빗물펌프장은 20년 빈도의 8,400 m3의 저수용량을 가지고 있으며, 신림2동 빗물펌프장은 30년 빈도의 5,300 m3의 저수용량으로 설계되었다. 신림5동 빗물펌프장은 수문일체형 펌프장으로서 분당 410 t의 물을 처리할 수 있는 고성능 펌프 3대가 설치되어 있으며 30년 빈도의 설계빈도를 갖는다.
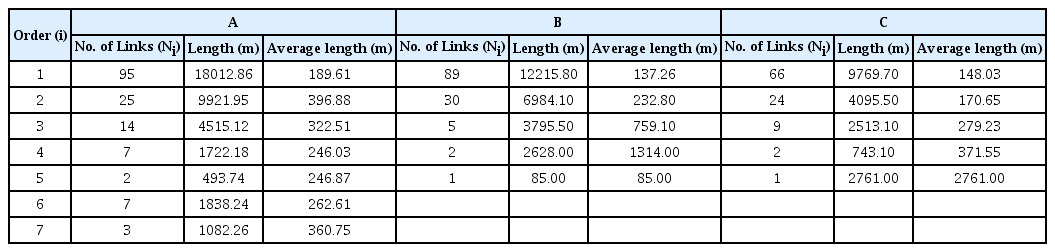
Table 1과 같이 A 유역은 유역면적이 약 8.92 km2이며, 711개의 소유역(Subcatchment), 620개의 노드(Node)와 632개의 관로(Link)로 구성되어 있다. 다른 대상유역과 비교하여 유역 내 관로의 총 길이가 가장 길다. B 유역의 면적은 14.32km2로 가장 크며, 667개의 노드와 686개의 관로로 이루어져 있다. 마지막으로 C 유역의 면적은 3.57 km2로 가장 작으며, 451개의 소유역과 517개의 노드, 503개의 관로로 이루어져있다. 도시적 성향을 가지고 있다는 점은 비슷하지만 도시 우수관망의 형상이나 유역의 면적, 특성들이 다른 유역들을 선정하여 연구를 진행하였다.
Statistics of Storm Sewer Networks in SWMM
4. 분석 및 결과
4.1 Horton-Strahler 차수법칙
유역의 분기비(RB)와 길이비(RL)를 산정하기 위하여, Horton-Strahler의 차수법칙을 이용하여 관로의 차수를 결정하는 작업이 수행되었다. 수계망에서는 두 가지 경로에서부터 합류되는 형태인 바이너리(Binary)형 노드가 존재한다.그러나 수계망과는 다르게 세가지 경로로부터 합류되는 노드도 존재하기 때문에 도시유역의 우수관망은 자연하천의 바이너리구조를 완전하게 만족하고 있지 않다. 따라서 본 연구에서는 관로의 차수 결정 시 세가지 관로로부터 합류되는 지점에서 2개 이상의 관로가 같은 차수 일 때 다음 차수로 발전해 나가는 것으로 정하였다. 차수별 관망은 아래 Fig. 3과 같이 나타내었다. 유역별 최고차수는 A유역은 7차, B유역과 C유역은 5차수로 산정되었고, 2개 이상의 같은 차수가 합류되는 노드는 A유역은 33개, B유역은 26개, C유역은 26개로 산정되었다.
Storm Sewer Networks in Catchments
산정된 우수관로의 차수 별 개수와 길이의 총 합을 이용하여 각 차수의 관로에 대한 평균 길이는 Table 2와 같이 산정되었다. 수계망과는 다르게 도시유역에 내린 빗물은 우수관으로 유입되어 배출하므로 건물이나 도로를 따라 우수관을 설계한다. 상류부의 말단부분까지 1차 관로가 길게 뻗어있는 특징을 가지고 있다. 따라서 높은 차수의 관로에 비해 1차 관로의 길이가 길어지게 되며 개수 또한 많아지게 된다.
Horton-Strahler Results for Catchments
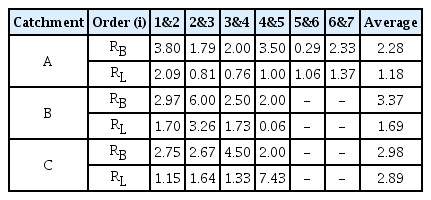
Table 3은 각 유역별 분기비(RB)와 길이비(RL)를 나타내었다. A유역을 제외한 B유역과 C유역의 분기비는 약 3.4와 3.0으로 수계망의 일반적인 범위인 3~5에 만족하는 것을 확인하였다. 길이비는 B유역과 C유역이 약 1.7과 2.9로 일반적 범위인 1.5~3.5의 범위를 만족하지만 A유역은 1.2로 만족하지 않는다. 이와 같은 결과는 B유역과 C유역이 A유역에 비교하여 수계망의 바이너리 형상에 더 가까운 구조를 가지고 있기 때문이다.
Law of Stream Numbers and Stream Lengths Result for Catchments
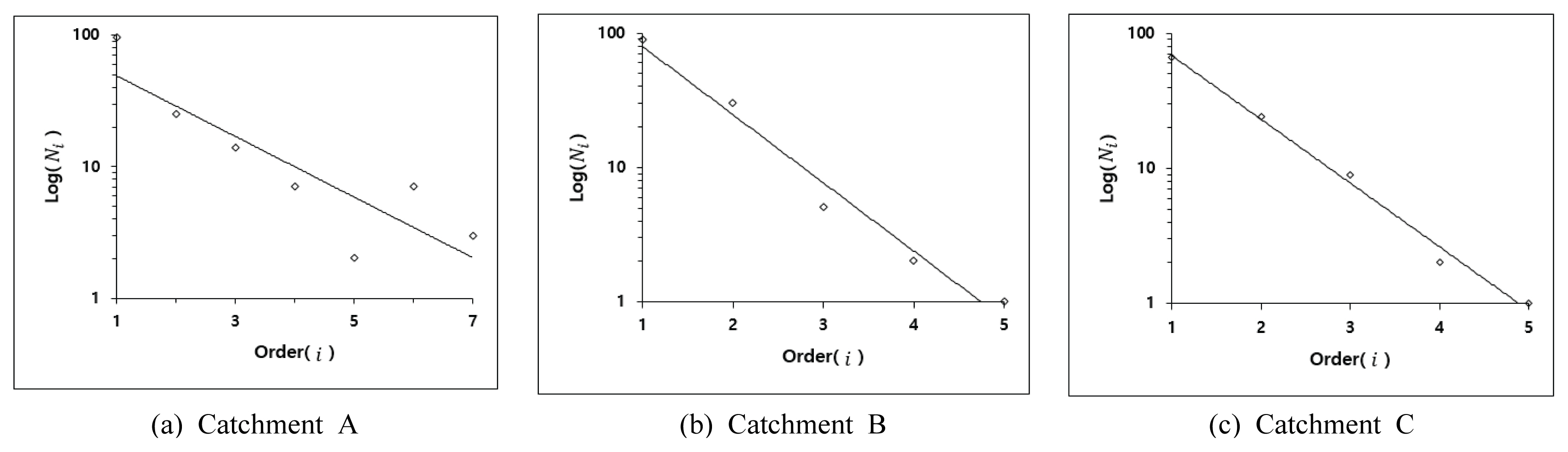
Figs. 4와 5와 같이 자연하천의 수계망에서 분기의 차수가 Horton의 분기의 법칙과 길이의 법칙과 다르게 완전한 선형을 이루지 않는 것을 확인할 수 있다. 자연하천의 수계망과 다르게 도시유역의 우수관망은 건물과 도로를 따라 관로를 설계하므로 우수관망의 말단부까지 1차 관로가 길게 뻗어있는 형태를 이루고 있다. 그러므로 1차 관로의 길이가 고차의 관로에 비해 길이가 길어지고 관로의 개수가 많아지기 때문에 Horton의 법칙을 완전히 만족시키지 못한다.
The Law of Stream Numbers for Catchments
The Law of Stream Length for Catchments
4. 결 론
본 연구는 도시 우수관망을 자연하천과 같이 복잡한 네트워크의 특성을 지닌 관망이라고 가정 하에 기존의 자연하천의 수계망에서 적용되는 개념들을 이용하여 적용하였다. 자연유역에 수계망에서 적용되는 Horton의 법칙을 이용하여 분기비 및 길이비를 산정하였고, Horton-Strahler 차수법칙 개념을 이용하여 우수관망의 차수를 분류하였다. A유역을 제외한 B유역과 C유역의 분기비는 수계망의 일반적인 범위인 3~5에 만족하는 것을 확인하였다. 길이비 또한 B유역과 C유역이 일반적 범위인 1.5~3.5의 범위를 만족하지만 A유역은 만족하지 못하였다. 이와 같은 결과는 B유역과 C유역이 A유역에 비교하여 수계망의 바이너리 형상에 더 가까운 구조를 가지고 있기 때문이다. 또한 수계망에서 Horton의 분기의 법칙과 길이의 법칙과 다르게 완전한 선형을 이루지 못하였다. 이는 유역의 우수관망의 1차 관로의 길이가 고차의 관로에 비해 길이가 길어지고 차수에 따른 관로의 개수가 많아지기 때문인 것으로 판단된다. 추후 본 연구에서 적용하였던 기존 이론 외에 다른 이론을 적용한 연구가 필요할 것으로 판단되며, 향후 도시 유역의 우수관 설계 시 우수관의 특성에 대한 기준도 제시한다면 보다 효과적인 우수관설 계와 도시 홍수 저감이 가능할 것으로 보인다.
Acknowledgements
본 연구는 국토교통부(국토교통과학기술진흥원) 건설기술연구사업 2014년의 ‘대심도 복층터널 설계 및 시공 기술개발(18SCIP-B089409-05)’ 연구단을 통해 수행되었습니다. 연구지원에 감사드립니다.