2017 포항 지진 시뮬레이션 모델 개발 및 시나리오 기반 지진재해지도 구축
Development of Simulation Model for the 2017 Pohang Earthquake and Construction of Hazard Map based on its Scenario
Article information
Abstract
규모 5.4의 포항지진은 2017년 11월 15일 발생하였다. 국내에서 계기 기록이 시작된 이래, 포항 지진은 가장 큰 경제적 피해와 인명 피해를 유발하였다. 한반도는 중약진 지역에 위치하며 관측된 강진 기록이 매우 제한적이다. 따라서 2017년 포항 지진에 의해 관측된 지반운동 기록은 가치 있는 지질 및 지진학적 정보이며 내진설계를 위한 중요 입력정보로도 활용될 수 있다. 본 연구에서는 점지진원 모델과 형태창 모델을 사용하여 2017년 포항 지진 평가하여 지진 시뮬레이션 모델의 개발 및 모델을 사용하여 시나리오 기반 지진 재해 지도를 구축하고자 한다.
Trans Abstract
The Pohang earthquake with a magnitude of 5.4 occurred on November 15, 2017. Since the advent of instrumental recording for earthquake ground motions in Korea, the Pohang earthquake has been the most damaging in terms of economic and life losses. Korea is located in a low-to-moderate seismic region so that occurrences of strong ground motions are extremely rare. Therefore, ground motions recorded during the Pohang earthquake could provide valuable geological and seismological information that can act as important inputs for seismic design. In this study, the 2017 Pohang earthquake has been estimated using the point source model and shaping window model. A contour map for peak ground acceleration is constructed for ground motions generated during the 2017 Pohang earthquake using the proposed simulation model.
1. 서 론
한반도는 지진 활동도가 높지 않은 유라시아판 내부에 속하며, 필리핀 판(Philippine Sea Plate), 태평양 판(Pacific Plate), 북아메리카 판(North American Plate)과 함께 4 개의 판이 상호작용하는 판 경계에서 약 400 km 거리에 위치하여 있다. 따라서 지진활동의 빈도가 판 경계에 속한 일본이나 미국 서부지역에 비해 작다. 그러나 강진의 발생 가능성은 존재하며, 최근 발생한 2016년 경주지진(ML=5.8), 2017년 포항지진(ML=5.4)은 국내에 많은 경제적 피해와 인명피해를 유발하였다. 이러한 지진 피해에 대비하기 위해선 일정 규모 이상의 지진에 의해 유발되는 지반운동의 특성과 관심 대상지역의 부지효과에 의한 증폭 특성에 대한 연구가 중요시된다. 그러나 기상청에 의해 1978년 이후 발생한 지진에 대해서만 관측 기록이 보고된 이후, 지반운동의 특성을 평가하기 위한 강진 지반운동 기록이 매우 부족한 실정이다. 이에 대해 해외의 선행 연구(Boore, 1983; Boore and Atkinson, 1987; Atkinson and Boore, 1995)는 Brune (1970, 1971)의 지진원 변위 스펙트럼 모델을 개발 및 개선하여 지반운동 푸리에 진폭 모델을 제안하여 지반운동의 특성을 평가 및 반영하여 이를 재현한 바 있다. 이 때, 적용할 수 있는 단층구조에 대한 정보가 부족할 경우 지진원을 점지진원으로 가정할 수 있다. 국내의 선행 연구(Jo and Baag, 2001, 2003; Junn et al., 2002)에서는 이러한 점지진원 기반 푸리에 진폭 모델을 이용하여 한반도 남부에서 발생한 지진 규모 2.1~4.3의 지진 특성을 평가하여, 지진 규모 4~8에 대한 감쇠식을 제안한 바 있다. 그러나 2016년 경주지진, 2017년 포항지진 등 중규모 지진의 강진 기록들의 PGA 감쇠 경향과 비교하여볼 때 진원거리 100 km이내에서는 실제보다 저평가하는 경향을 보였다. 따라서 최근 기록된 강진 기록을 포함한 지진의 특성이 재평가되어야 할 것으로 판단된다.
보통 지질지반 조건의 공간적인 분포와 관련된 부지효과는 지진 발생 시 지반운동의 증폭에 큰 영향을 준다(Sun et al., 2012). 이는 암반 지층에 비해 퇴적 지층일 경우 더 크게 영향을 주는 것으로 알려져 있다. 포항지역은 퇴적 지층으로 알려져 있어 부지 증폭효과가 발생하여 그 피해가 컸음을 추정할 수 있다(Eem et al., 2018). 그리고 부지효과는 주파수 영역에서 지반운동 특성 평가시 형태를 왜곡하기 때문에 추가로 고려될 필요가 있다. 이에 대해 선행 연구(Castro et al., 1997; Zhao et al., 2006)는 Nakamura (1989)가 제안한 수평-수직 스펙트럼 비(Horizontal to vertical spectrum ratio, HVSR) 방법을 개선하여 제안한 바 있다.
본 연구에서는 2017년 포항 지진의 본진과 2018년에 발생한 여진을 평가 분석하기 위해 국가지진종합정보 시스템 (NECIS)에서 제공하고 있는 지진 관측 자료를 활용하였으며, 125개의 누적 관측소에서 기록한 375개의 관측기록을 선정하여 지진파의 형상, 강진 지속시간, 주파수 특성을 포함한 다양한 지진 특성과 부지 증폭 특성을 분석하였다.
Fig. 1은 지진의 진앙지와 평가 관측소 사이의 지진파 전파 경로를 나타낸 것이다. 그리고 Table 1에 연구에 사용한 지진의 발생일시와 위치, 진원 깊이, 지진 규모와 평가 관측소개수를 나타냈다. 이 때, 잡음에 의해 왜곡된 자료를 제외하기 위해 Kalkan (2016)이 개발한 PPHASE PICKER를 이용하여, 진폭에 대한 신호 대 잡음비(Signal to noise ratio, SNR)가 10 이상인 기록을 선정하였다.
2. 점지진원 모델을 지반운동 평가
2.1 점지진원 모델의 이론적 배경
Boore (1983)은 지반운동의 가속도 진폭 스펙트럼에 근접한 진폭 스펙트럼을 갖는 특정 잡음(windowed white gaussian noise)을 시간영역에서 생성하는 방법을 제안하였다. 지반운동 가속도를 생성하기 위한 모델식은 Brune (1970, 1971)의 진폭 스펙트럼 기반으로 제안되었으며, 이후 Boore and Atkinson (1987), Atkinson and Boore (1995)에 의해 개선되었다. 기존 점지진원 모델식은 지반운동 기록이 부지효과에 의한 영향을 적게 받는 암반 지역을 대상으로 제안되었으나, 국지적인 부지효과의 영향을 받는 관측소를 추가로 고려하여 평가하였기 때문에 이러한 영향을 고려하기 위해 본 연구에서는 지반 증폭 계수항 [Z(f)]을 추가로 고려하였다(Jee and Han, 2018). 따라서, 이를 반영한 주파수 영역에서의 지반운동 푸리에 진폭 스펙트럼의 모델식 [A(f)]은 Eq. (1)과 같다.
여기서, C는 푸리에 진폭 스펙트럼의 단위 및 크기를 결정하기 위한 배율조정계수 (scaling factor)로서 Eq. (2)와 같다.
여기서, <RθΦ>는 지진 발생시 방사(radiation)되는 SH파의 평균방사상수(= 0.44)이다(Boore and Boatwright, 1984). F는 지진파의 자유면 효과를 고려한 값 (= 2)이다. V는 지반운동의 수평성분을 벡터 분할하기 위한 값(= 0.7071)이다. Rref는 지진원에 대한 기준거리로 1 km로 고려하였다. ρ. β는 지진원 근처의 지각 밀도와 S파의 전단파 속도를 나타낸 값으로 한반도를 대상으로 Kim (1995)이 제안한 값을 적용하여 각각 2.7 g/cm3, 3.36 km/s를 적용하였다. S(f)는 지진원 변위 진폭 스펙트럼의 형상을 결정하기 위한 함수(Source spectral function)로서, Eq. (3)과 같다.
Mo는 지진 모멘트(seismic motion) 값이다. Hanks and Kanamori (1979)는 Mo와 지진 모멘트 규모(seismic motion magnitude), MW의 관계식을 제안하였으며, Eq. (4)와 같다.
fc는 진폭 스펙트럼의 모서리 주파수 값으로 Boore (1983)는 다음과 같은 Eq. (5)를 제안하였다.
여기서, ∆σ는 지진 전후 지진원 근처의 응력 강하 값이다.
D(f)는 지진의 진원거리, 주파수에 따른 감쇠함수(Diminution function)로, 국내의 선행연구(Park et al., 2000; Jo and Baag, 2001, 2003; Park et al., 2001; Junn et al., 2002)는 Boore and Atkinson (1987)과 Anderson and Hough (1984)의 수식을 기반으로 다음과 같은 수식으로 정리하였으며, Eq. (6)과 같다.
여기서, κ는 거리에 따른 감쇠 매개변수이다.
G(R)는 지진파 방출 시 거리에 따른 기하학적인 확산을 나타내는 값으로 진원거리의 역수 R-1로 정의하였다. I(f)는 지반운동의 유형을 결정하기 위한 필터 함수(filter function)로 Eq. (7)과 같다.
여기서, p는 각각 0(변위), 1(속도), 2(가속도)에 대한 변수값이다.
Z(f)는 대상 지역의 부지효과를 고려하기 위한 지반 증폭계수항(site amplification factor function)으로서, 이에 대한 선행연구(Castro et al., 1997; Zhao et al., 2006)에서는 각 관측소 별로 측정한 지반운동의 수평성분과 수직성분의 비율 (HVSR)로서 제안하였다.
Castro et al. (1997)은 각 지진 관측소별로 지반운동의 상시 미동(microtremors)을 활용하여, 수평 성분의 푸리에 진폭 스펙트럼과 수직 성분의 푸리에 진폭 스펙트럼 성분의 비율(H/V Fourier spectral ratio)로서 부지 증폭 효과를 고려하였다. 그러나, 이 방법(H/V Fourier spectral ratio)을 사용하기 위해선, 시간영역이 충분히 긴 계측자료를 사용하여야 하며, 비교적 분산이 크고 급격한 형상을 갖기 때문에, 추가로 평활화(smoothing)작업이 수행되어야 한다. Zhao et al. (2006)는 대신에 5% 감쇠비가 적용된 수평 성분과 수직성분의 응답 스펙트럼의 비(H/V response spectral ratio)를 사용할 것을 제안하였으며, 이는 Eq. (8)과 같다.
여기서, RSAV(f), RSAH(f)는 각각 5% 감쇠비가 적용된 지반운동 수직 성분과 기하평균 적용된 수평 성분의 응답 스펙트럼이다.
2.2 점지진원 모델을 이용한 지진 특성 평가
지진에 의한 지진파의 전파(propagation)에 따른 감쇠특성과 진원(ref: 1 km)에서의 푸리에 진폭 스펙트럼 특성을 평가하기 위해, 앞서 구축된 모델식을 기반하여 2017년 포항지진의 본진 및 여진의 지진 특성을 평가하였다. 평가하기에 앞서, 지진 관측 기록 자료는 100초 구간을 사용하였다. 지반운동 기록은 초당 100 샘플을 가진 데이터이며, 안티앨리어싱 필터(40 Hz, 대응주기 0.025 초)가 적용되어 있어서 추가로 버터워스 고역통과 필터(0.1 Hz, 대응주기 10 초)를 적용하였다. 또한 암반 지역이 아닌 관측소에서 측정된 지반운동의 진폭 스펙트럼의 왜곡을 피하기 위해, 모든 계측지반운동 가속도의 부지효과를 제거한 푸리에 진폭 스펙트럼 [Rrecord(f)]을 산정하였으며, Eq. (9)과 같다.
여기서, Arecord(f)는 관측소에서 기록한 수평성분 지반운동 기록의 벡터성분을 고려하기 위해 기하평균 적용된 푸리에 진폭 스펙트럼이다.
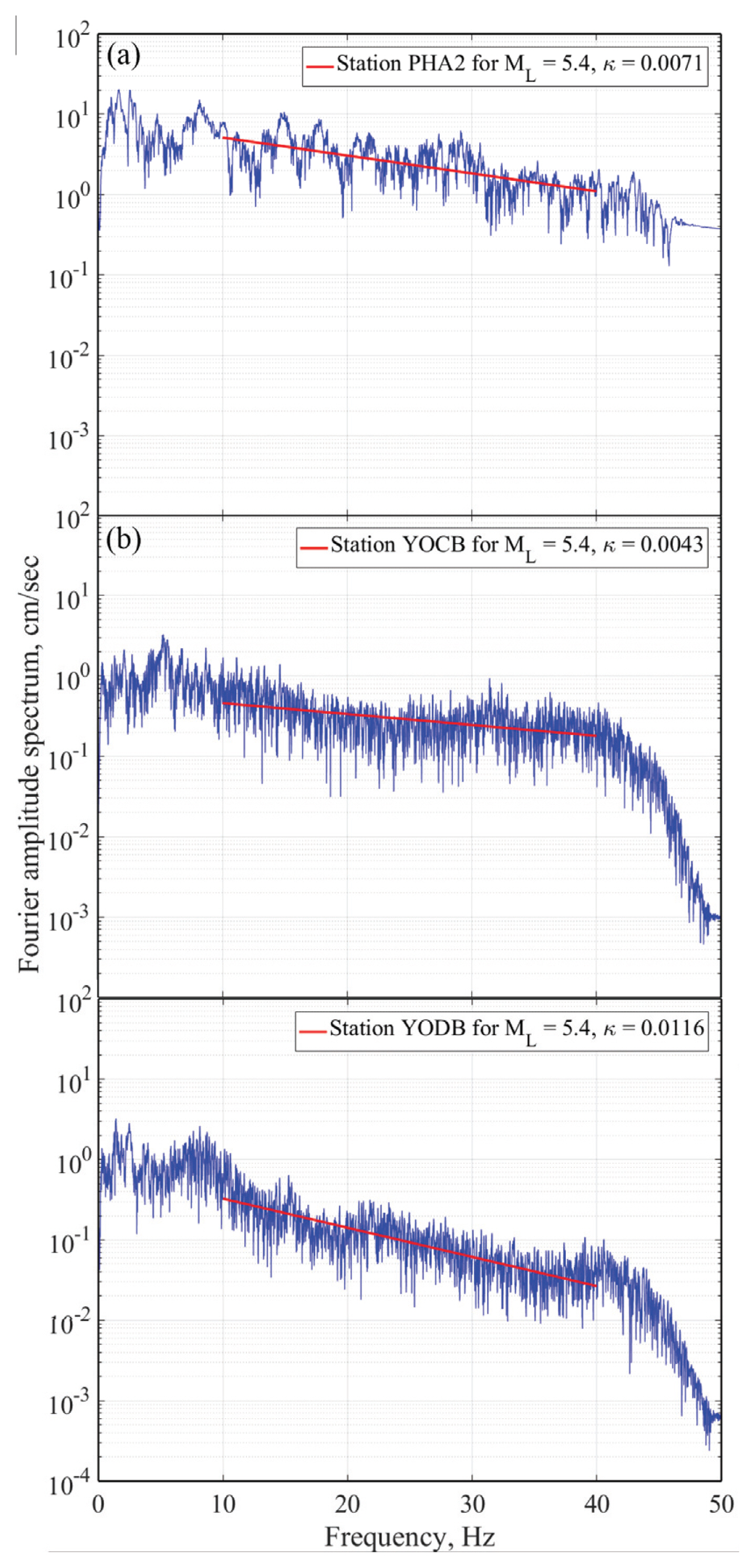
모델식에서 지반운동 파형의 전파에 따른 감쇠 특성을 대표하는 주요 매개변수는 κ이다. κ는 비탄성 감쇠효과와 지반여건에 따른 진폭 스펙트럼감쇠효과를 포함한 일종의 high-cut filter역할을 하며, 확률론적 방법을 기반으로 생성한 인공 지반운동에 사용된다(Junn et al., 2002). κ는 유효한 주파수 범위(y축: log-scale, x축: normal-scale)에서 지반운동 가속도의 푸리에 진폭 스펙트럼의 기울기, (-πκ)에서 산정할 수 있다(Anderson and Hough, 1984). Eq. (9)을 통해, 부지 증폭효과를 제거한 진폭 스펙트럼을 기반으로 감쇠매개변수, κ를 산정하였다. Fig. 2는 2017년 포항 지진의 본진의 지반운동 기록을 관측한 관측소의 감쇠 매개변수 평가를 대표로 나타낸 것이다.
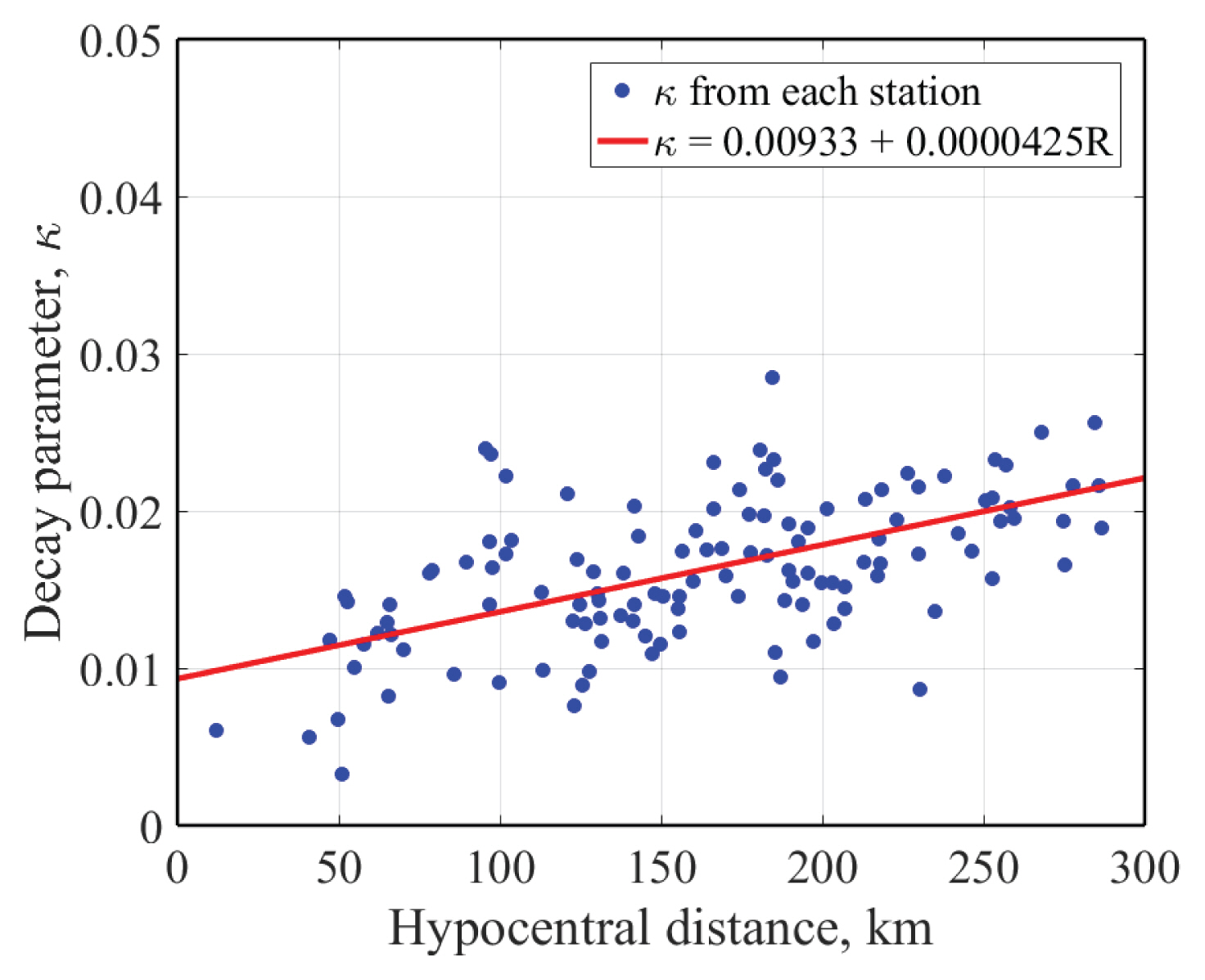
Fig. 2는 2017년 포항지진 본진 발생시 관측한 관측소(PHA2, YOCB, YODB) 별 지반운동 기록의 푸리에 진폭 스펙트럼 값이며, 유효 주파수 범위는 10 - 40 Hz로 판단하여 감쇠 매개변수, κ를 계산하였으며, 각각 0.0071, 0.0043, 0.0116이다. Fig. 3은 포항지진의 본진과 여진을 고려하여 평가한 감쇠 매개변수 값과 회귀선을 함께 나타낸 것이다. 평가된 감쇠매개변수에 대한 진원거리 관계식은 Eq. (10)과 같다.
진원에서의 푸리에 진폭 스펙트럼 특성에 따른 매개변수는 지진 모멘트, Mo 및 지진 모멘트 규모, MW, 모서리 주파수, fc, 지진원에서의 응력강하, ∆σ이며, 이는 지진원의 푸리에 진폭 스펙트럼 모델식 [C×S(f)]을 기반으로 평가할 수 있다. 이를 위한 선행연구(Boore, 1983; Atkinson and Boore, 1998; Joshi et al., 2016)는 Brune (1970, 1971)의 지진원 변위 진폭 스펙트럼 이론을 기반으로, 지진원의 가속도 푸리에 스펙트럼을 구하는 방법을 제안하였다.
또한, 본 연구에서는 부지효과가 제거된 지진원 변위 스펙트럼 [Srecord(f)]을 구하기 위해, 관측소별 부지효과를 추가로 고려하였으며, Eq. (11)과 같이 정리된다.
모델식을 사용하여 지반운동을 재현하기 위해서는 지진원에 의한 Brune (1970, 1971)가 제안한 모델식의 모서리 주파수, fc가 주로 사용된다. fc는 관측된 지반운동을 Eq. (11)을 이용하여 계산한 변위 진폭 스펙트럼을 이용하여 산정할 수 있다(Jo and Baag, 2001). 이는 Andrews (1986)가 제안한 방법을 이용하여 평가할 수 있으며, Eqs. (12~15)과 같다.
Eqs. (12) and (13)를 각각 계산한 적분 값 J, K를 이용하여, 변위 진폭 스펙트럼의 저주파수 극한값인 Ωo을 구할 수 있으며, Eq. (14)와 같다.
Jo and Baag (2001)은 저주파수 극한 값, Ωo의 초기값을 U(ω1)으로 설정한 뒤, Eqs. (12~14)을 이용하여 반복 계산하는 방법을 제안하여 안정된 Ωo 값을 계산할 수 있도록 하였다. 모서리 주파수, fc는 아래 Eq. (15)을 이용하여 계산 할 수 있다.
지진원 변위 진폭 스펙트럼의 형상은 Eq. (3)을 이용하여 계산할 수 있으며, 이 때 필요한 매개변수는 모서리 주파수, fc과 지진 모멘트, Mo이다. Joshi et al. (2016)은 변위 진폭 스펙트럼을 구하기 위한 절차를 소개한 바 있으며, Brune (1970, 1971)의 ω-2 모델 식을 이용하여 지진 모멘트, Mo을 계산하는 방법을 제안하였으며, Eq. (16)과 같다.
Fig. 4는 2017년 포항 지진의 본진의 지반운동 기록을 관측한 관측소의 변위 진폭 스펙트럼 [Srecord(f)]과 Eqs. (15) and (16)로 평가한 매개변수를 반영한 변위 진폭 스펙트럼의 모델 식 [C×S(f)]을 대표로 비교하여 나타낸 것이다.
Fig. 4 (a~f)는 2017년 포항지진 발생시 관측한 관측소(PHA2, YODB, YEYB, MIYA, MAS2, JINA)별 지반운동 기록의 지진원 변위 진폭 스펙트럼 값이며, 계산된 매개변수 fc, Mo는 각각 0.94Hz, 1.09x1024 dyn-cm (PHA2), 0.66Hz, 0.94x1024 dyn-cm (YODB), 0.42Hz, 3.63x1024 dyn-cm (YEYB), 1.22Hz, 0.59x1024 dyn-cm (MIYA), 1.24Hz, 0.95x1024 dyn-cm (MAS2), 0.68Hz, 4.22x1024 dyn-cm (JINA)이다.
Fig. 5는 2017년 포항 지진의 본진과 여진을 고려하여 평가한 매개변수 fc, Mo 값과 Eq. (5)에 의해 역산된 응력강하, ∆σ (= 1, 10, 100, 1000 bar) 선을 함께 나타낸 것이다.
Table 2는 점지진원 모델을 사용하기 위한 지진 특성 매개변수를 2017년 포항지진의 본진과 여진 이벤트별로 정리하여 나타낸 것이다. 지역규모, ML=5.4의 본진(EQ. 2)의 경우, 모멘트 규모, MW, 모서리 주파수, fc와 응력 강하, ∆σ는 각각 5.5, 0.5779 Hz, 76.47 bar로 평가되었으며 지역규모, ML=4.6의 여진(EQ. 1)의 경우는 각각 4.5, 1.5259 Hz, 55.78 bar로 평가되었다.
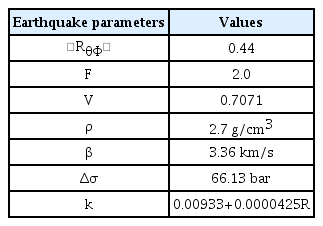
Table 3은 점지진원 모델에 대한 지진 특성 매개변수를 평가하여 정리한 것이다. 이 때, 평가된 응력 강하 값은 포항 지진의 본진과 여진을 평균하여 제시하였다. Kanamori and Anderson (1975)은 판경계 지역에서는 응력 강하 값으로 30 bar, 판 내부 지역에서는 100 bar를 얻었다. 따라서 평가된 응력강하 값, 66.13 bar는 판 경계지역에서 어느 정도 떨어져 위치한 한반도에 대해서는 타당한 값으로 판단된다.
3. 지반운동 형태창 모델 지반운동 평가
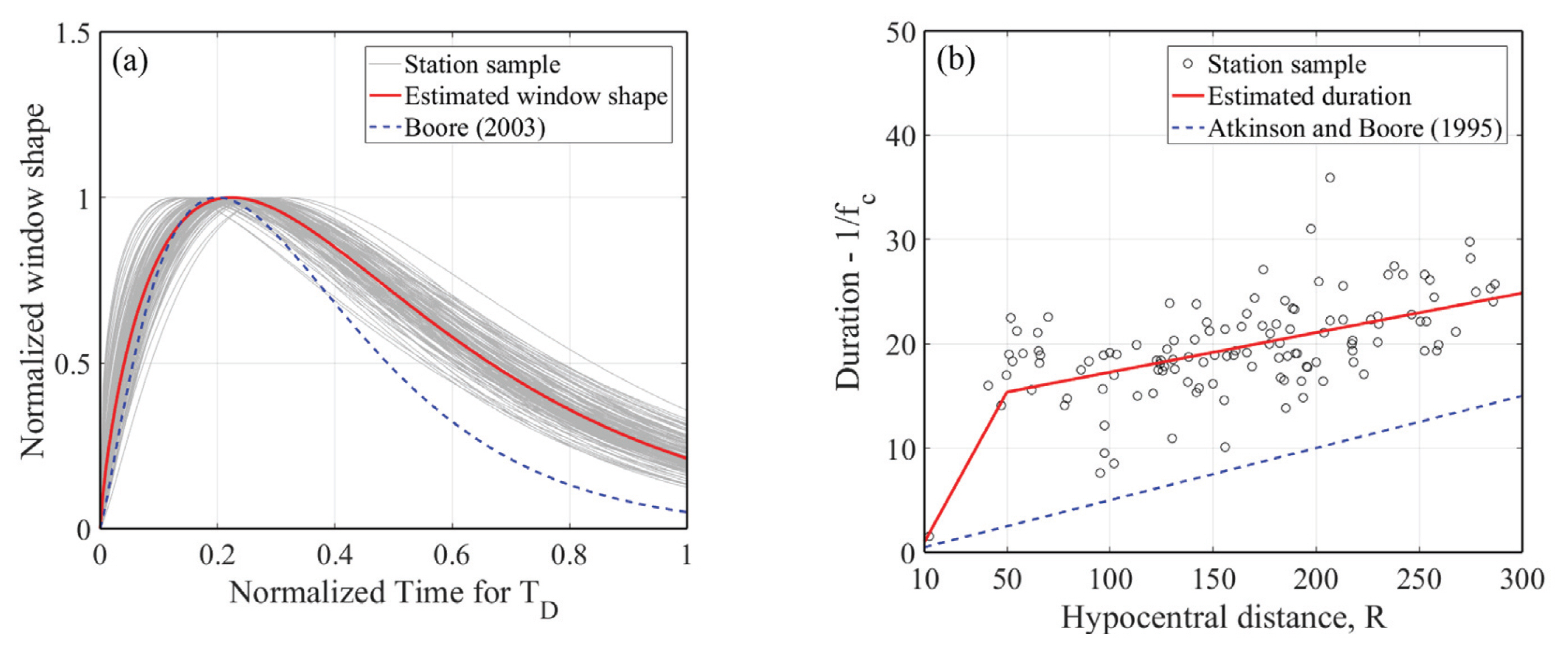
점지진원 모델을 이용한 지반운동 생성 시, 지진파의 규모와 진원거리에 따른 인공 지반운동을 생성하기 위해선 시간영역에서 적절한 형태창(shaping window)을 갖는 특정 잡음(windowed white gaussian noise)을 설정하여야 한다(Jo and Baag, 2003). 이에 대해, Boore (2003)은 Saragoni and Hart (1974)가 제안한 형태창 모델에 매개변수를 추가하여 사용하였으며, Atkinson and Boore (1995)는 강진 지속시간 모델식을 제안한 바 있다. 그러나, 이는 미국 동북부의 지반운동 관측 기록을 평가하여 제안된 식으로 국내 관측기록과 비교하였을 때 잘 맞지 않는 경향을 보였다. 따라서 한반도 지반여건에 맞는 지진을 개발하기 위해 형태창 모델 [W(t)]을 제안하였으며, Eq. (17)과 같다.
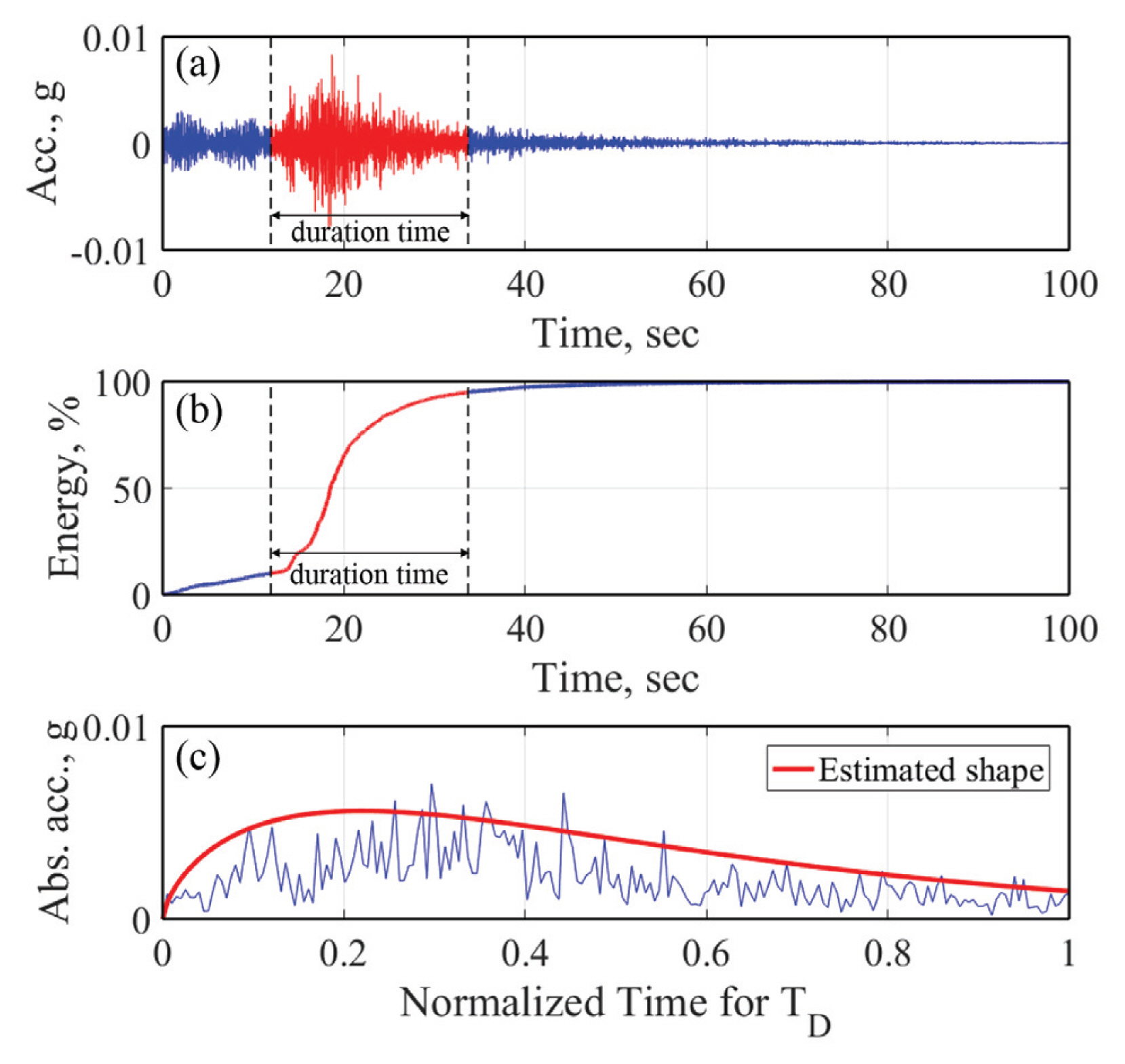
여기서, t는 시간, TD는 강진 지속시간이다. 강진 지속시간을 고려하기 위해, 정규화된 Arias Intensity Energy [E(t)]를 평가하여 S파 도달시점과 총 에너지의 95%의 도달시점간격을 계산하였으며, Eq. (18)과 같다(Fig. 6).
여기서, Acc(t)는 시간에 따른 지반운동의 가속도 값이다.
Fig. 6은 2017년 포항지진 본진에 대한 OKCB 관측소 기록을 평가하여 나타낸 것이며, 지속시간은 21.78초로 평가되었다. 이와 같은 방식으로 Eqs. (17) and (18)을 사용하여 각 지진 이벤트별 지반운동 관측기록의 형태와 강진 지속시간을 평가하여 Fig. 7에 나타내었다. Fig. 7(a)는 지반운동 가속도 기록의 형상을 Eq. (17)을 이용하여 평가한 것이다. 이 때, Eq. (17)의 매개변수, c0, c1, c2는 각각 1.9626, 0.7859, -3.5131로 평가되었다. Fig. 7(b) 관측기록별 모서리 주파수가 고려된 강진 지속시간과 평가식을 함께 비교하여 나타낸 것이다.
지속시간 평가에 관한 선행연구(Boore and Atkinson, 1987; Boatwright and Choy, 1992; Atkinson and Boore, 1995)는 지반운동의 강진 지속시간은 모서리 주파수와 진원 거리에 관한 식을 제안한 바 있다. 따라서, 본 연구에서는 다음과 같이 지속시간 [TD]에 관한 식을 제안하였으며, Eq. (19)와 같다.
Fig. 7에 나타난 바와 같이, 미국 동북부를 대상으로 평가한 지반운동 모델은 2017년 포항 지진 관측 기록을 저평가하고 있다. 따라서 본 연구에서는 한반도 지반여건에 부합하도록 새롭게 평가한 모델을 사용하여 지반운동 생성 시뮬레이션을 개발하였다.
4. 부지효과를 고려한 지진 시뮬레이션 구축
4.1 지진 시뮬레이션 모델 구축
2017년 포항 지진 특성을 반영한 지반운동을 생성하기 위해서 앞 절에서 평가한 점지진원 모델과 지반운동 형태창 모델을 사용하여 Boore (2003)가 제안한 방법에 따라서 지반운동을 생성하였으며, Fig. 8에 이에 대한 절차를 나타내었다. 점지진원 모델을 사용하여, 인공 지반운동을 생성하기 위해, 먼저 특정 잡음(white gaussian or uniform noise)을 생성한다(Fig. 8(a)). 그리고 앞 절에서 평가한 형태창 모델을 적용하여 잡음의 형상을 결정한다(Fig. 8(b)). 푸리에 변환 방법을 사용하여 잡음을 주파수 영역으로 치환한다(Fig. 8(c)). 제곱평균제곱근(root mean square, RMS) 방법을 사용해서 정규화한다 (Fig. 8(d)). 정규화된 잡음의 푸리에 스펙트럼에 점지진원모델을 곱하여 지진 특성을 반영한다(Fig. 8(e)). 푸리에 역변환을 사용하여 시간 영역으로 변환하여 인공 지진파를 생성한다(Fig. 8(f)). Safak and Boore (1988)는 잘못된 순서로 인공지진파를 생성할 경우 장주기에서 지반운동이 왜곡될 수 있음을 나타낸 바 있다.
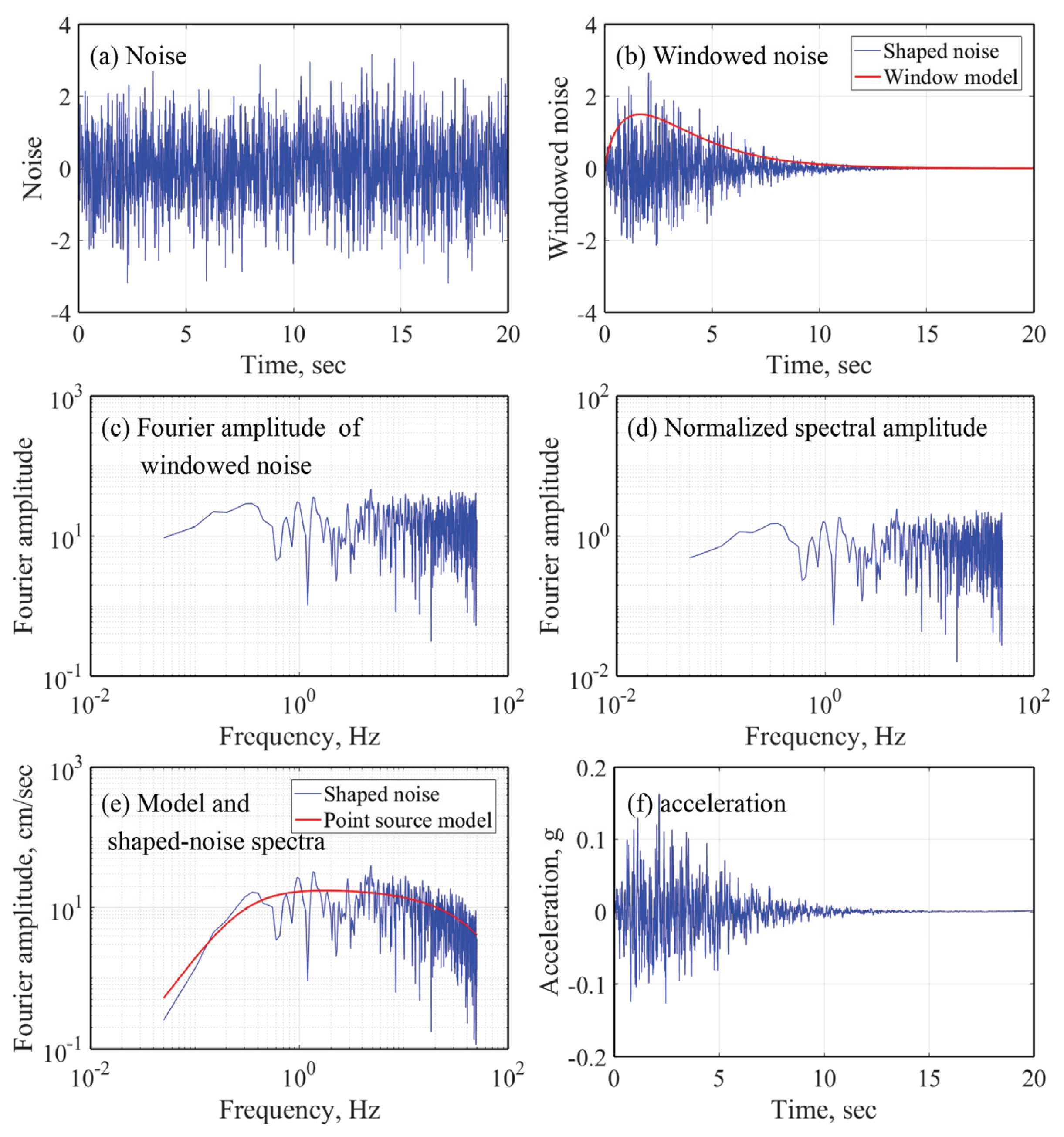
Basis of the Time-domain Procedure for Simulating Ground Motions using the Stochastic Method Without Site Amplification for MW = 6.0, R = 10 km (Boore, 2003)
4.2 지진 관측소별 지반운동 생성
앞 절에서 제안된 지진 시뮬레이션 모델과 절차를 기반으로 지진 특성 매개변수(지진 모멘트 규모, 진원거리, 부지별 증폭 효과 등)을 수치해석 프로그램인 MATLAB 소프트웨어를 사용하여 지반운동 가속도 기록을 관측소별로 다수(200개) 생성하였다. 생성된 지반운동 가속도 기록의 타당성을 검증하기 위하여 임의의 관측소 3곳(PHA2, YODB, USN2)에서 기록된 수평 성분의 관측기록을 평가하여 비교하였다(Fig. 9). 이 때, 생성된 지반운동은 각 관측소별 평가된 지진파 형상과 지속시간을 사용하여 생성되었으며, 이에 대해 산정된 수평 성분의 평균 강진 지속시간은 각각 2.6초, 15.6초, 24초이다. Fig. 9(a-c, f-h, k-m)은 각각 관측소별 시간영역에서의 관측 기록과 생성된 기록의 샘플을 비교하여 나타내었다. Fig. 9(d, i, n)은 지반운동 생성시 반영된 주파수별 지반 증폭 값을 나타낸 것이다. 또한, 주기 영역에서 각 관측소별 계측된 수평 성분의 지반운동 기하평균 응답 스펙트럼과 함께 생성된 지반운동 가속도의 응답 스펙트럼의 중간 값을 비교하여 나타낸 것이다.
또한, 각 관측소별로 전반적으로 스펙트럼의 크기와 형상이 유사한 것으로 보이나, 일부 주기 별 편차가 보이는 것을 확인할 수 있었다. 이는 단층에서의 지반 동특성, 지진의 방사 패턴, 전파 특성 등의 여러 불확실성 요인에 의한 것으로 판단되어 추가로 지반운동 응답 스펙트럼의 편차를 고려하였다. 지반여건에 맞는 지반운동 가속도를 생성하기 위해선, 지반여건이 고려된 편차 값이 필요하다. 그러나, 이러한 편차는 국내에선 강진 기록에 대해 평가한 연구가 매우 적어 평가하여 사용하기 힘든 실정이다. 따라서, 한반도와 같은 판 내부지역에 속하는 미국의 동북부(ENA) 지역의 규모 4.3-7.6지진에 대해 Atkinson (2008) 이 평가한 표준편차 값을 고려하였다. Atkinson (2008)은 5% 감쇠비 적용된 응답스펙트럼의 표준편차를 상용로그(log (base 10) unit)영역에서 각 주기별로 0.22~0.38로 평가하였다. 본 연구에서는 모든 주기에 대해서 표준편차를 상용로그 영역에서 0.3 (=σlog)의 편차 값을 적용하였다(Jee and Han, 2018).
관측된 지반운동에 대해, 생성된 지반운동의 응답 스펙트럼의 평균적인 편차를 고려하기 위해 Jee and Han (2018)이 제안한 방법을 통해 평가하였으며 Eq. (20)과 같다.
여기서, Err (Estimated error)는 상용로그 영역에서의 이차평균 편차 값으로 지반운동 기록의 관측 값과 생성 값의 차이를 나타낸 것이다. Saobs, Saarti는 각각 관측소별 관측된 기록의 기하평균 응답 스펙트럼 값과 인공 지반운동의 중간값 응답 스펙트럼 값이다. Tn은 n번째로 고려된 주기 값이며, 0.01~10초 사이의 31개의 주기영역에서 평가하였다. 각 관측소(PHA2, YODB, USN)에 대하여 각각 0.50σlog, 0.60σlog, 0.54σlog으로 나타났으며 Fig. 9(e, j, o)에 편차와 같이 나타냈다. 이 때, 평가된 편차는 고려된 편차 이내로 보이기 때문에 유효하게 재현 가능한 것으로 판단된다.
4.3 부지 효과를 고려한 지진 재해지도 구축
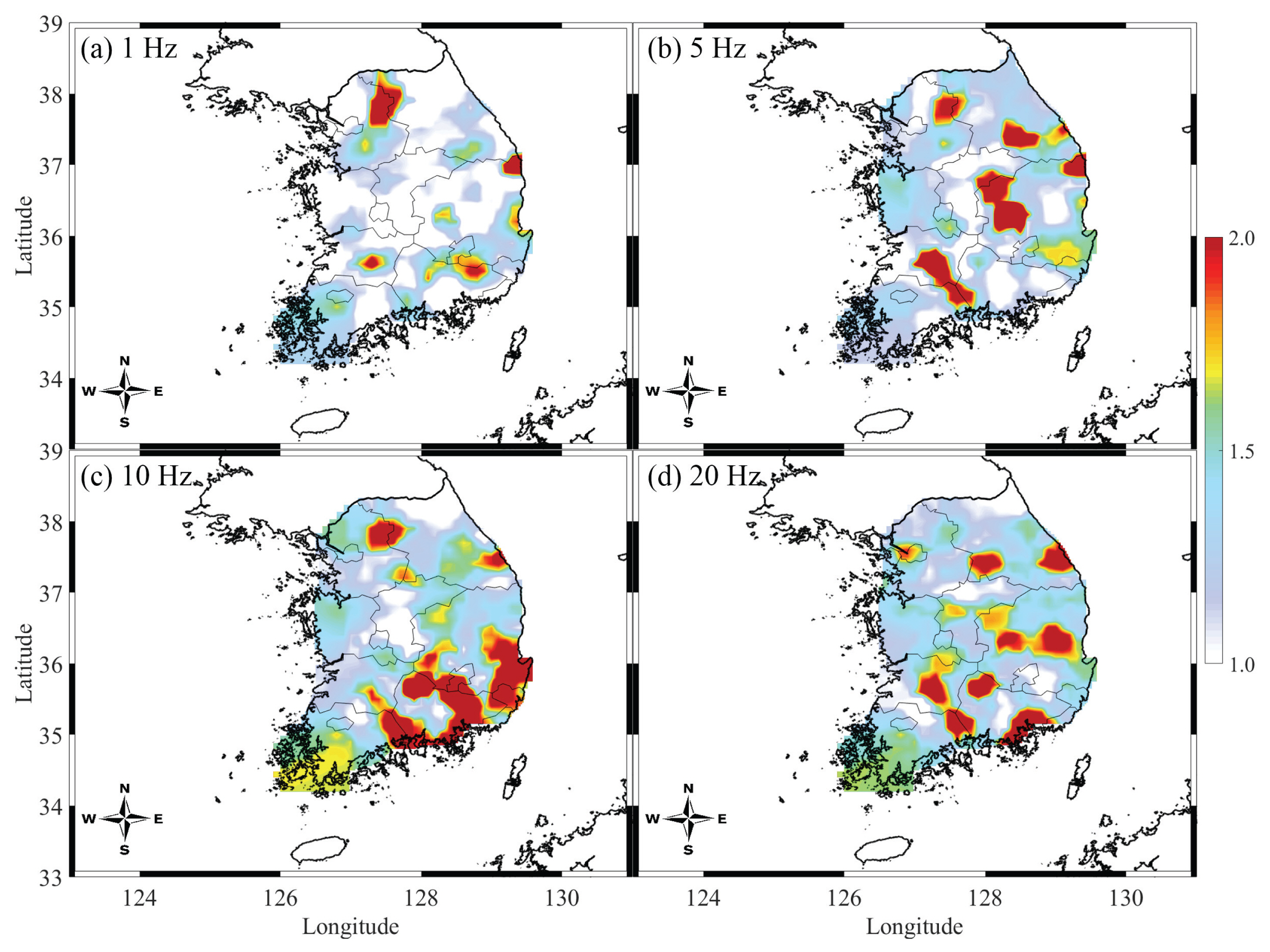
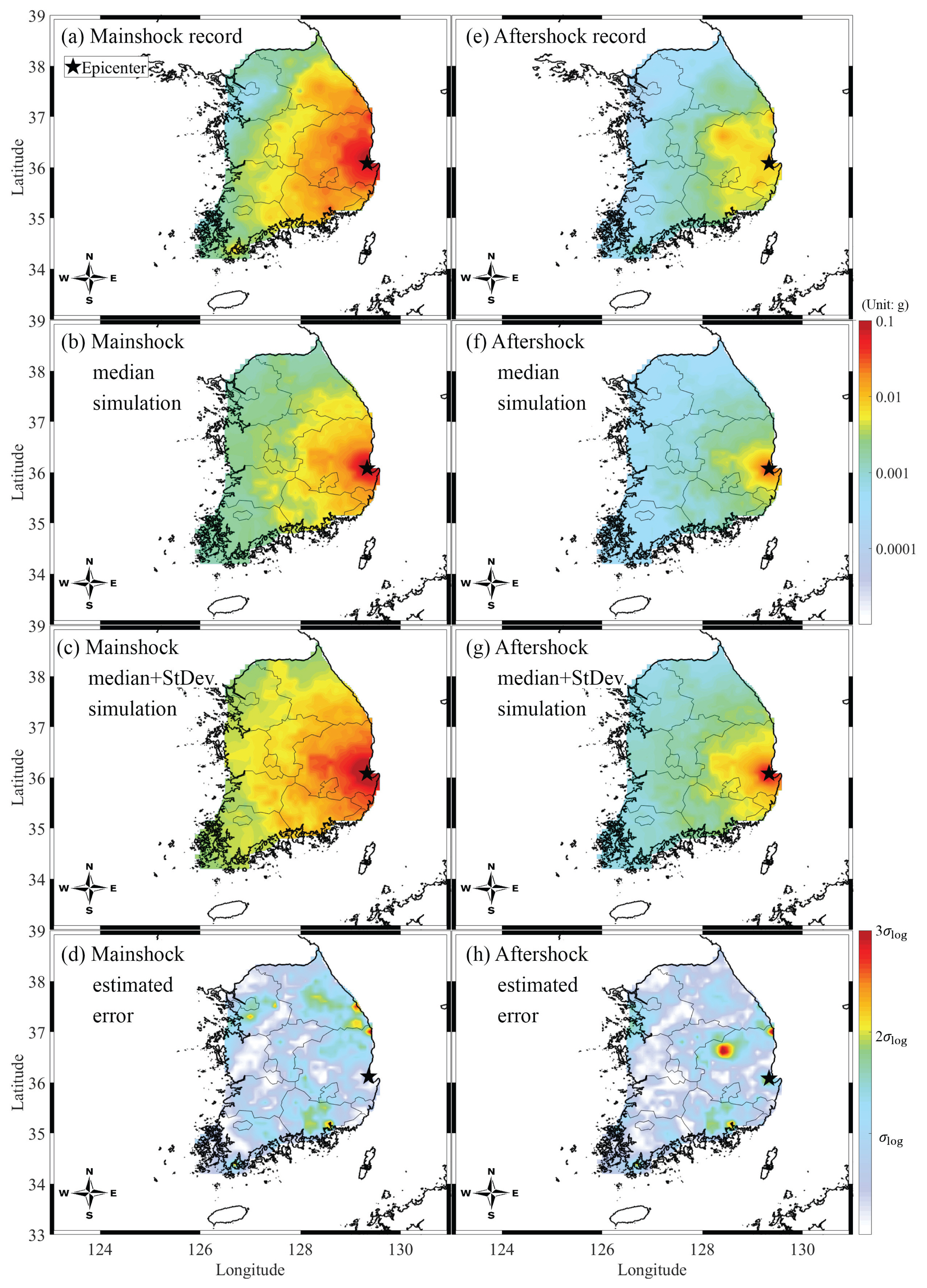
일반적으로 지진 발생을 관측한 지반 운동은 대상 지역의 고유 부지효과로 인해 증폭한다. 이는 지질의 공간적인 분포와 관계되어있다(Sun et al., 2012). 또한 암반 지반에 비해 토사 지반에서 그 증폭 정도가 크며 결과적으로 구조물에 큰 피해를 유발할 수 있다. 그리고 2017년 포항 지진이 발생하였을 때, 관측소에서 이러한 부지 효과의 영향을 받아 증폭된 지반운동 관측 값이 기록된다. 본 연구에서는 앞서 평가된 관측소별 부지효과와 지질공간정보를 이용하여 한반도 전역에 대해, 관측소 별 지반 증폭 계수를 보간법(interpolation), 외삽법(Extrapolation)을 사용하여 공간적으로 분포시켰다. 이 때, 0.1º × 0.1º 격자 간격으로 가장 가까운 3개의 관측소에 대하여 거리의 역수 값을 취해 가중평균을 수행하여 지반증폭을 평가하였다(Fig. 10). Fig. 10은 고려 주파수(1Hz, 5 Hz, 10 Hz, 20 Hz)별 한반도 전역에 대해 분포된 지반증폭효과를 나타낸 것이다. 여기서 포항 및 경주 지역이 포함된 한반도 남동부 지역은 지반증폭의 정도가 타 지역에 비해 높게 평가되어, 구조물의 피해 정도가 상대적으로 클 것으로 판단된다. 공간적으로 평가된 지반증폭 정보를 반영하여 한반도 전역에 대하여, 2017년 포항지진의 본진 및 여진에 의한 지반운동을 생성하여, 최대지반 가속도(Peak ground acceleration, PGA) 지진 재해도를 구축하여 실제 기록과 함께 나타내었다(Fig. 11). Fig. 11 (d, h)는 실제 기록과 생성된 지반운동 PGA의 중간 값을 비교하여 한반도 전역에 대해 공간적으로 나타낸 것이며, 일부 지역을 제외한 대부분의 지역에서 2σlog이내로 평가되었다. 따라서 본 연구에서 개발한 지진 시뮬레이션 모델은 타당하며 한반도 전역에 대해 지반운동 생성이 가능한 것으로 판단된다.
5. 결 론
본 연구에서는 점지진원 모델과 지반운동 형태창 모델을 기반으로 한반도 남부에서 발생한 2017년 포항 지진의 본진과 여진의 지진 특성 및 지반 분류에 따른 부지효과를 평가하여 지진 시뮬레이션 모델을 개발하였다. 또한 이를 반영하여 한반도에 대한 시나리오 기반 2017년 포항 지진의 본진과 여진지진 재해 지도를 추가로 구축하였으며 결과는 다음과 같다.
(1) 부지효과가 제거된 푸리에 진폭 스펙트럼 모델식을 이용하여, 한반도의 지반여건을 대표하는 지진파의 전파에 따른 감쇠 특성 (κ), 지진원에서의 응력강하(∆σ)를 평가하였다. 이 때, 부지효과에 의한 국지적인 지반 증폭효과를 고려하기 위하여, 관심 대상지역에서 관측 기록된 지반운동 가속도 자료를 이용하여 모델식을 제안하였다.
(2) 그리고 시간영역에서 형태창 모델을 사용하여 지반운동의 형태 및 지속시간을 평가하였으며 이를 반영하여 지진 시뮬레이션 모델을 개발하였다.
(3) 지진 시뮬레이션 모델의 타당성을 평가하기 위해, 2017년 포항 지진의 지반운동 가속도 관측 기록과 생성된 지반운동의 최대지반가속도 재해도를 작성하여 공간적으로 편차를 비교하였다. 그 결과, 생성된 PGA 재해도는 실제 기록을 재현할 수 있다고 평가된다.
(4) 제안된 지진 시뮬레이션 모델은 한반도 전역으로 적용이 가능하며, 이는 확률론적 지진위험지도 작성 시 입력지진에 사용되는 등, 지진 공학 연구의 유용한 기초자료로 사용할 수 있을 것이라 판단된다.
Acknowledgements
본 연구는 한국연구재단의 지원(NRF-2017R1A2B3008937)에 의하여 수행된 것으로 이에 감사드립니다.