Monte Carlo 모의실험을 이용한 Burr XII 분포형의 적용가능성에 관한 연구
Applicability of Burr XII Distribution for Rainfall Frequency Analysis using Monte Carlo Simulation
Article information
Abstract
수공구조물의 설계 및 관리에 있어서 확률강우량을 산정하는 것은 매우 중요하며, 특히 강우 빈도해석을 수행할 때 수문자료를 적절하게 표현할 수 있는 최적의 확률분포형을 선정하는 것은 매우 중요하다. 수문통계분야에서는 generalized extreme value (GEV), generalized logistic (GLO), Gumbel (GUM) 분포와 같은 다양한 분포 모형을 널리 사용하여 왔다. 우리나라 극한 강우사상의 경우 GEV 분포와 GUM 분포가 비교적 적합한 것으로 알려져 있다. 하지만 GEV, GLO, GUM 분포와 같이 기존에 사용하던 분포형은 하나의 형상매개변수 혹은 형상매개변수가 없어 자료의 통계적 특성을 정확하게 표현하는데 한계가 있을 수 있다. 반면에 Burr XII (BUR) 분포는 두 개의 형상매개변수를 가지고 있어 분포형이 나타내는 통계적 특성의 범위가 넓은 장점이 있다. 또한, 다양한 분야에서 유연하게 적용할 수 있는 통계적 특성을 가지고 있기 때문에 최근 수자원 분야에서도 이를 적용하기 위한 다양한 연구가 진행되고 있다. 따라서 본 연구에서는 우리나라 강우자료에 대하여 BUR 분포를 적용하여 적합도 검정을 수행하였고, 기존에 사용되고 있는 분포형의 결과와 비교⋅분석하였다. 또한 Monte Carlo 모의실험을 이용하여 BUR 분포형의 적용 가능성을 확인하였다. 그 결과 GEV 및 BUR 분포형이 GUM 및 GLO 분포형과 비교하여 적합한 것으로 나타났다.
Trans Abstract
Hydrological quantile estimation is crucial for the design and management of hydraulic infrastructure. In the frequency analysis of extreme rainfall, it is important to select the most appropriate probability distribution that can adequately reproduce the extreme rainfall quantiles. In statistical hydrology, various distributions such as the generalized extreme value (GEV), generalized logistic (GLO), and Gumbel (GUM) distributions have been used widely. The GEV and GUM distributions are often suggested as the appropriate probability models for data on cases of extreme rainfall in Korea. However, the GEV, GUM, and GLO distributions have a limit for reproducing the statistical characteristics of data because they either have one shape parameter or do not have one at all. However, the Burr XII (BUR) distribution has two shape parameters and has a high flexibility for fitting data. Therefore, it has been widely used in the hydrological field and others. In this study, the applicability and suitability of the BUR distribution were examined for annual maximum rainfall data in Korea. The performance of the BUR distribution was compared with those of the conventional distributions using the Monte Carlo simulation. As a result, it was found that the GEV and BUR distributions are more appropriate models for Korean extreme rainfall data compared to the GUM and GLO distributions.
1. 서 론
최근 기후변화로 인하여 과거 통계자료의 일반적인 범위를 벗어나는 극한 가뭄 및 홍수가 빈번하게 발생하고 있다. 이러한 이상 기상현상은 자연재해와 밀접하게 연관되어 있어서 사회⋅경제적으로 영향을 미칠 수 있는 중요한 요인이다(Houghton et al., 2001). 따라서 극한 가뭄 및 홍수에 효과적으로 대응하기 위하여 수공구조물의 설계 시 다양한 방법을 적용하여 안전성을 확보하는 방안이 크게 부각되고 있다. 일반적으로 수공구조물의 설계에 가장 기초적이고 근간이 되는 절차는 확률강우량 산정이다. 표본으로부터 추출된 수문자료에 대하여 다양한 확률분포형을 적용하고, 대상 자료를 적절하게 나타낼 수 있는 확률분포형을 선정해야 한다. 선정된 확률분포형에 따라 확률강우량이 결정되기 때문에 적합한 확률분포형을 선정하는 것이 매우 중요하다(Heo, 2016). 확률분포형이 수문자료를 적절하게 표현하려면 확률분포형이 표현할 수 있는 통계적 특성의 범위가 넓어야 한다. 이를 위하여 수문자료의 다양한 통계적 특성을 적절히 표현할 수 있는 확률분포형을 개발하고, 적용하기 위한 연구가 꾸준히 진행되고 있다. 수문통계 분야에서는 극치 수문사상을 해석하고 보다 적합한 확률강우량을 산정하기 위하여 각 국가별 또는 지역별로 다양한 확률분포형을 적용하고 있다. 미국 수자원평의회(U.S. Water Resources Council, 1976)는 홍수빈도해석 수행 시 log-pearson type III (LP3) 분포를 권장하고 있으며, 호주의 Australian Rainfall and Runoff (The Institution of Engineers, 2001) 보고서에서도 LP3 분포를 사용하여 확률강우량을 산정하고 Intensity-Depth-Frequency (IDF) 곡선을 유도할 것을 권고하였다. 영국의 경우 Flood Studies Report (NERC, 1975)에서 지역홍수빈도해석 시 Generalized extreme value (GEV) 분포를 추천하였으나 이후 Flood Estimation Handbook (IH, 1999)서는 Generalized logistic (GLO) 분포를 사용할 것을 권장하고 있다. 국내에서는 우리나라 22개 지점을 대상으로 연 최대 강우자료를 이용하여 적정 분포모형을 선정한 결과 최적 분포모형으로 GEV 분포가 선정된 바 있다(Heo and Kim, 1995; Kim et al., 1996). 또한 「한국 확률강우량도 작성(MOCT, 2000)」에서는 GUM 분포형을 우리나라 대표 강우 확률분포모형으로 추천하였고, 「확률강우량도 개선 및 보완 연구(MLTM, 2011)」에서도 적정 확률분포형으로 GUM 분포를 채택하고 있다. Lee, Lee, et al. (2000), Heo et al. (2007) 등의 연구에서는 GUM 분포와 GLO 분포를 지역빈도해석의 최적분포형으로 채택한 바 있다.
확률분포형이 극한 수문사상을 보다 명확하게 해석하기 위해서는 확률분포형에서 좌⋅우로 치우쳐진 극한사상을 잘 표현할 수 있어야 한다. 즉, 주어진 표본 자료의 왜곡도를 적절히 표현할 수 있어야 하고 이를 위해선 표본자료의 왜곡도와 직접적인 연관이 있다고 알려진 형상매개변수(shape parameter)의 역할이 매우 중요하다. 하지만 기존에 사용된 대부분의 확률분포형들은 하나의 형상매개변수를 가지고 있어서 확률분포형이 표현할 수 있는 통계적 특성 범위에 한계가 있다. 이러한 한계점을 극복하기 위하여 상대적으로 많은 매개변수를 이용하여 다양한 형태의 왜곡도를 고려할 수 있는 kappa와 Wakeby 분포에 대한 다양한 연구가 진행되었다(Lee et al., 1998; Lee, Song, et al., 2000; Oh, 2001; Maeng et al., 2006; Heo et al., 2012). 그러나 kappa와 Wakeby 분포는 다양한 표본 자료에 대해 비교적 안정적인 매개변수를 추정할 수 있으나 상대적으로 많은 매개변수로 인하여 매개변수 추정에 대한 불확실성이 높고 매개변수 추정방법과 적합성 조건에 따라 이용에 불편함이 존재하는 단점이 있다(Melching et al., 1987; Kim et al., 2004; Kuo et al., 2008; Heo et al., 2012; Na et al., 2014).
한편, Burr XII 분포는 1942년에 Burr에 의해 제안된 분포로 type I부터 XII까지 12가지 형태로 구분되어 있다(Burr, 1942). 이 중에서 Burr XII 분포는 초기에 2변수 분포모형으로 보험계리학(Klugman, 1986; Embrechts et al., 1997), 임학(Lindsay et al., 1996), 환경(Shao, 2000), 신뢰성 분야(Wang et al., 1996; Wingo, 1983, 1993), 생존분석(Shao and Zhou, 2004)과 같이 다양한 분야에서 적용되고 그 우수성이 검증되었다. 하지만 수문통계 분야에서는 2변수 Burr XII 분포와 다른 확률분포형과의 연관 관계에 대해서 연구가 진행되었고(Burr and Cislak, 1968; Rodriguez, 1977; Tadikamalla, 1980), 이후 수문자료에 대한 적용성을 높이기 위해 규모매개변수(scale parameter)가 추가된 3변수 형태의 Burr XII 분포가 개발되었다(Tadikamalla, 1980; Shao, 2004). 특히 Shao et al. (2004)이 제시한 extended Burr XII (BUR) 분포는 기존의 Burr XII 분포를 확장하여 한 개의 규모매개변수와 두 개의 형상매개변수를 갖는 3변수 분포로 기존 Burr XII 분포와 달리 표본자료가 갖는 다양한 범위의 첨예도와 왜곡도를 고려할 수 있는 것으로 알려져 있다. Shao et al. (2004)는 BUR 분포를 중국 남부지역의 주강(Pearl River) 유역과 북동부의 Dang Jian Kou River 유역의 홍수자료에 적용하여 기존에 사용하던 LP3 분포나 generalized Pareto (GPA) 분포보다 더 우수한 결과를 확인하였고, Ganora and Laio (2015)는 이탈리아 북서쪽유역 115개 지점의 홍수자료에 적용하여 BUR 분포형의 적용성 및 우수성을 검증한 바 있다. 우리나라에서도 Seo et al. (2017)은 BUR 분포형을 우리나라 강우자료에 적용하여 L-moment ratio diagram을 분석함으로써 한강유역에서 적용성이 우수한 것으로 검증한 바 있다.
본 연구에서는 BUR 분포의 특성을 살펴보고자 우리나라 강우자료의 빈도해석에 주로 사용되는 GEV, GUM, GLO 분포와 BUR 분포를 이용한 적합도 검정을 수행하였고 검정 결과를 비교⋅분석하였다. 또한 Monte Carlo 모의실험을 이용하여 BUR 분포형의 적용 가능성을 정량적으로 검토하였다.
2. 기본이론
2.1 확률분포모형
2.1.1 Burr XII 분포
본 연구에서 사용된 BUR 분포는 Shao et al. (2004)에 의해 소개된 분포형으로 기존 2변수 BUR 분포를 확장하여 한 개의 규모매개변수와 두 개의 형상매개변수를 가지는 특징이 있으며, 기존 2변수 BUR 분포보다 다양한 왜곡도와 첨예도를 가지는 표본에 대해 적용이 가능한 장점이 있다. 3변수 BUR 분포의 누가분포함수와 확률분포함수는 다음 Eqs. (1)∼(2)와 같이 나타낼 수 있다(Shao et al., 2004; Ganora and Laio, 2015).
여기서 α는 규모매개변수이고, β와 β1은 형상매개변수이다. x의 범위는 β≤0 일 때 0≤x<∞이고, β>0 일 때는
2.1.2 Gumbel 분포
GUM 분포는 최대치 혹은 최소치 등 극치 자료의 빈도해석에 주로 사용되며, 홍수량 또는 강수량 자료의 빈도해석에 많이 이용된다. GUM 분포의 누가분포함수와 확률분포함수는 다음 Eqs. (3)∼(4)와 같이 나타낼 수 있다(Hosking and Wallis, 1997).
여기서 μ는 위치매개변수(location parameter) 그리고 α는 규모매개변수 이다. x의 범위는 -∞ < x < ∞이다.
2.1.3 Generalized Extreme Value 분포
GEV 분포는 극치 수문사상 빈도해석에 주로 사용되는 분포모형으로 앞서 언급한 GUM 분포와 더불어 우리나라 강우사상에 적합한 것으로 알려져 많이 사용되고 있다. 특히 GUM 분포와 비교하여 형상매개변수의 존재로 극치 수문자료에 보다 유연하게 적용할 수 있다. GEV 분포의 누가분포함수와 확률분포함수는 다음 Eqs. (5)∼(6)과 같이 나타낼 수 있다(Hosking and Wallis, 1997).
여기서 α는 규모매개변수, β는 형상매개변수 그리고 μ는 위치매개변수이다. x의 범위는 β = 0일 때 -∞ < x < ∞이고 β > 0, β < 0 일 때는 μ + α/β 값에 의해 상한과 하한이 정해진다. 또한 GEV 분포는 β = 0 조건에서는 GUM 분포가 되고 β > 0에서는 Weibull 분포, 그리고 β < 0인 경우는 Fréchet 분포가 되는 특징을 가지고 있다.
2.1.4 Generalized logistic 분포
GLO 분포는 2변수 logistic 분포의 일반화된 모형으로 kappa 분포의 특수한 형태이다. 최근 지역빈도해석에서 사용이 증가하고 있는 확률분포형으로 기존의 GEV 분포보다 확률밀도함수의 오른쪽 꼬리부분이 두꺼운 특징을 가지고 있다. GLO 분포의 누가분포함수와 확률분포함수는 다음 Eqs. (7)∼(8)과 같이 나타낼 수 있다(Hosking and Wallis, 1997).
여기서 α는 규모매개변수, β는 형상매개변수 그리고 μ는 위치매개변수이다. x의 범위는 β = 0일 때 -∞ < x < ∞이고 β > 0, β < 0일 때 μ + α/β 값에 의하여 상한과 하한이 정해진다.
2.2 매개변수 추정
본 연구에서는 매개변수 추정방법으로 L-moment 방법을 이용하였다. L-moment 방법은 차수가 다른 확률가중모멘트(Probability weighted moments, PWM)를 선형으로 가중하여 편의가 제거된 모멘트를 구하는 방법으로 일반 모멘트법과 유사하게 사용되며 확률분포모형의 매개변수를 추정할 수 있다. PWM은 변수값과 변수의 평균값과의 차이를 모멘트의 차수에 따라 거듭제곱하여 모멘트를 계산하며, Eq. (9)와 같이 정의된다(Greenwood et al., 1979).
여기서 x(F)는 quantile function이고 s는 모멘트의 차수이다. BUR 분포의 PWM은 Hao and Singh (2009)에 의해서 유도되었으며, β값은 양의 값을 가질 수 없는 것이 특징이다(Hao and Singh, 2009). Burr XII 분포의 PWM은 Eq. (10)과 같다.
여기서 Γ(∙)는 감마 함수를 나타내며, L-moment λ1, λ2, λ3, λ4를 PWM의 선형조합으로 표시하면 다음 Eqs. (11)∼(14)와 같다(Landwehr et al., 1979; Hosking and Wallis, 1997).
Eqs. (11)∼(14)를 이용하여 L-moment 비를 다음 Eqs. (15)∼(17)과 같이 구할 수 있다(Hosking and Wallis, 1997).
L-CV와 L-skewness를 무차원화하고 이들의 상관관계를 통해서 형상매개변수 β와 β1을 구할 수 있으며(Ganora and Laio, 2015), 본 연구에서는 Seo et al. (2017)에 의해 유도된 L-moment와 L-moment ratio를 사용하였다. BUR 분포의 규모매개변수와 각각의 형상매개변수를 구하는 식은 다음 Eqs. (18)∼(22)와 같다.
여기서 τ는 표본의 L-CV를 나타내며, 사용된 GEV, GUM, GLO 분포의 매개변수는 Hosking and Wallis (1997)의 방법을 참고하여 추정하였다.
2.3 적합도 검정
적합도 검정(goodness-of-fit test, GOF test)은 대상 자료로부터 얻어지는 분포와 가정한 확률분포형이 얼마나 잘 일치하는가를 검정하는 것이다. 모집단의 확률분포형을 알지 못하면 기존의 확률분포형으로 모집단의 성질을 정확히 나타내기 어려우므로 다양한 기법을 통해서 많은 정보를 이용하여 적절한 확률분포형을 선정하는 것이 합리적이다(Shin et al., 2010). 확률밀도함수에 대해서는 χ2-test, 누가분포함수에 대해서는 Kolmogorov-Smirnov (K-S) test 방법을 이용하여 적합도 검정을 수행하였다.
2.3.1 χ2-test
χ2-test는 대상 자료에 적합하다고 가정한 확률밀도함수와 군집화된 자료를 이용한 빈도해석을 통하여 구해지는 경험적 확률밀도함수를 비교하는 검정방법으로, 자료를 크기에 따라 m개의 계급 구간으로 나누고 이론값과 자료값의 절대 도수를 비교하는 방법으로 검정통계량 q는 다음과 같다.
여기에서 nj는 관측 자료의 j번째 구간의 표본 관측 도수, ej = npj는 확률분포의 j번째 구간의 이론도수이며, m은 계급 구간의 수를 나타낸다. 또한 pj는 구간 내 특정 기각치를 만족하는 모의변수확률로, 유의수준 α에 대해 귀무가설이 q≥K로 기각된다고 하면 P(q≥K;q~χ2(k=1)) = α로 정의되며 K = χ2(k-1)으로 계급 구간을 나눈 후 결정된다. 계산된 통계량은 χ2 <
2.3.2 Kolmogorov-Smirnov test
K-S test의 기본적인 절차는 주어진 표본자료의 누가분포함수와 가정된 이론적 확률분포모형의 누가분포함수를 비교하는 것으로 양자의 최대편차가 표본의 크기와 유의수준에 따라 결정되는 한계편차보다 크면 해당 분포가 기각되는 검정 방법이다.
여기서 Sn(x)는 자료를 크기순으로 재배열했을 때의 k번째 자료의 이론적 누적발생확률, n은 자료의 총 개수이다. 전체 구간의 Sn(x)와 F(x)의 최대 편차는 Dn = max|F(x) - Sn(x)|로 계산한다. 최대편차 Dn은 n의 크기에 따라 좌우되는 확률변수로서 유의수준 α에 따라 적합성이 결정된다.
2.4 Log likelihood
우도(likelihood)는 확률분포함수에서 모수가 어떤 확률변수의 자료와 일관되는 정도를 나타내는 값이다. 즉, 모분포에서 해당 자료에 대하여 부여하는 확률로 다음과 같이 나타낼 수 있다.
Log likelihood(logL)는 likelihood 함수에 로그 함수를 씌운 것으로, 확률 변수가 독립 확률 변수로 나누어지는 경우와 같이 확률 분포 함수가 곱셈 꼴로 나올 때 미분계산의 편의성을 위해 주로 사용된다. 본 연구에서는 분포형 간 적합성을 비교하기 위하여 각 분포형의 매개변수는 L-moment법을 이용하여 추정하였고 log likelihood 값(logL)을 사용하여 분포형을 평가하였다. 각 분포형에서 산정된 logL 값을 비교하여 logL 값이 클수록 분포형이 모의한 자료를 잘 표현한다고 판단할 수 있다.
3. 적용 및 결과
3.1 방법론
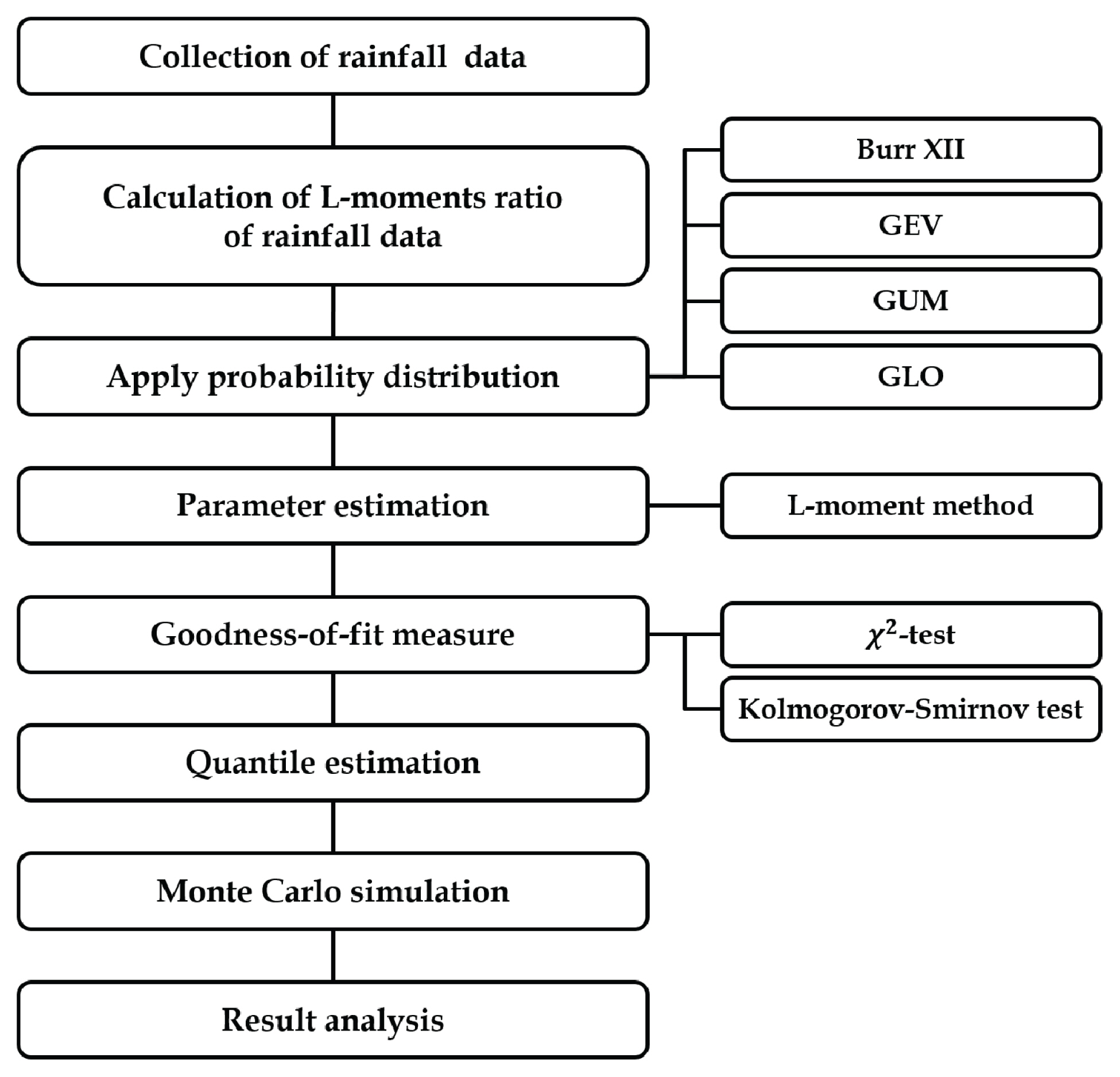
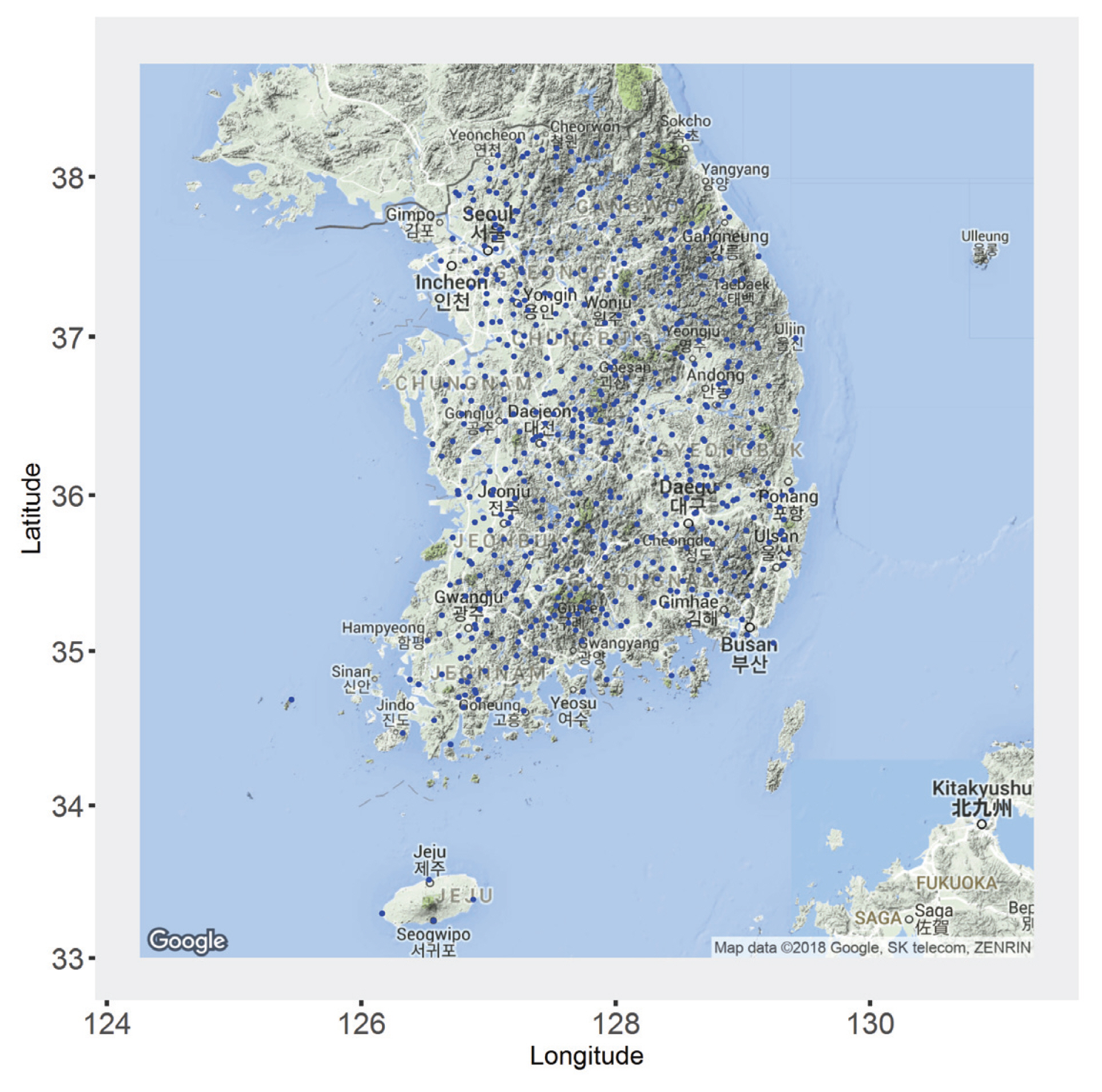
Fig. 1은 본 연구의 흐름을 나타낸 것으로 우리나라 강우자료에 대하여 BUR 분포형의 적용 가능성을 검토하고자 24시간 연 최대 강우자료를 이용하여 적합도 검정을 수행하였다. 또한, BUR 분포형의 적용성을 검토하고자 Monte Carlo 모의실험을 이용하였고, 각 지점의 관측값으로부터 추정된 매개변수를 kappa 분포형에 적용하여 자료를 발생하고 GEV, GLO, GUM, BUR 분포형에 적합시켜 log likelihood를 계산한 값을 기준으로 적절한 분포형을 판단하였다. 본 연구를 수행하기 위하여 국토교통부, 기상청, 한국수자원공사 등의 우리나라 617개 지점에서 24시간 연 최대 강우 자료를 수집하였다. 수집된 연 최대 강우 자료는 한강 유역 212개, 낙동강 유역 206개, 금강 유역 117개, 그 외(섬진강, 영산강 유역) 82개 지점으로 구성되어 있으며 각 지점의 위치는 Fig. 2와 같다.
3.2 적합도 검정 결과
전술한 바와 같이 우리나라 617개 지점을 대상으로 적용한 분포형별 χ2-test와 K-S test를 통과한 지점의 수는 Table 1과 같다. Table 1에서 χ2-test 결과를 살펴보면 GUM 분포형이 적합도 검정을 통과하는 지점수가 570개로 다른 분포형과 비교하여 상대적으로 작게 나타났으며, 다른 분포형의 적합도 검정 통과 지점 수는 같게 나타났다. 또한, GUM, GEV, GLO, BUR 분포형은 모든 지점에서 K-S test를 통과하는 것으로 나타났다. 이는 지속시간 24시간 강우자료의 빈도해석에는 GUM 분포형 보다는 GEV, GLO, BUR 분포형을 이용하는 것이 극치 수문자료의 통계적 특성을 나타내는데 적합할 것으로 판단된다. 또한, BUR 분포형은 GEV, GLO 분포형과 동일한 지점들에서 적합도 검정을 통과하는 것으로 나타났으며, 적합도 검정을 통과한 지점에 대하여 BUR 분포형을 적용하여 확률강우량을 산정하는 것에 문제가 없을 것으로 생각된다.
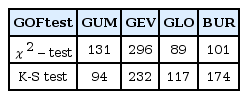
Table 2에는 적합도 검정 시 가장 작은 검정통계량으로 검정을 통과한 최적의 분포형을 선정하였고, 각 분포형별로 선정된 지점 수를 정리하였다. 일반적으로 K-S test 보다 기각력이 우수하다고 알려진 χ2-test 결과를 살펴보면 GEV 분포는 296개로 가장 많은 지점에서 검정통계량 값이 가장 작게 나타났다. BUR 분포는 101개로 GUM 분포형 보다 보다 적지만 GLO 분포형 보다는 많은 지점에서 선정되었다. 또한, K-S test에서는 BUR 분포가 174개 지점에서 검정 통계량 값이 가장 작게 나타났고, GEV 분포형에 이어 두 번째로 많은 지점에서 선정된 것을 확인할 수 있다.
3.3 Monte Carlo 모의실험
본 연구에서는 각 분포형에 대한 적용성을 검토하기 위하여 Monte Carlo 모의실험을 수행하였고, 관측값으로 추정된 매개변수는 kappa 분포형에 적합시켜 모의자료를 발생시켰다(Hosking and Wallis, 1997). 500회 반복수행하여 얻어진 모의발생 값을 각 분포형에 적용하여 log likelihood 값을 산정하였다. Table 3은 모의발생한 자료를 이용하여 log likelihood 값을 각 분포형별로 산정하여 비교하였을 때 채택된 횟수를 나타낸 것으로, GEV 분포형이 617개 지점 중에서 447개 지점(약 72.45%)에서 1순위(First)로 채택되었다 다음으로 BUR 분포형은 170개 지점(약 27.55%)에서 1순위로 채택되었으며, GUM, GLO 분포형은 1순위로 채택된 지점이 없는 것으로 나타났다. GEV 분포형을 1순위로 채택한 지점 중 2순위(Second)로 BUR 분포형이 채택된 지점은 294개이고, GUM 분포형과 GLO 분포형은 각각 111개, 42개 지점에서 채택되었다. 또한 BUR 분포형을 1순위로 채택한 지점 중 2순위로 GEV 분포형은 158개 지점, GLO 분포형은 17개 지점에서 채택되었다. BUR 분포형은 GEV 분포형에 이어서 채택비율이 두 번째로 높게 나타나며 다른 분포형(GUM, GLO)과 비교하여 우리나라 극치 수문자료의 통계적 특성을 잘 나타내는 것으로 생각된다. 즉, BUR 분포형은 우리나라 강우자료 빈도해석에 적용이 가능할 것으로 판단된다.
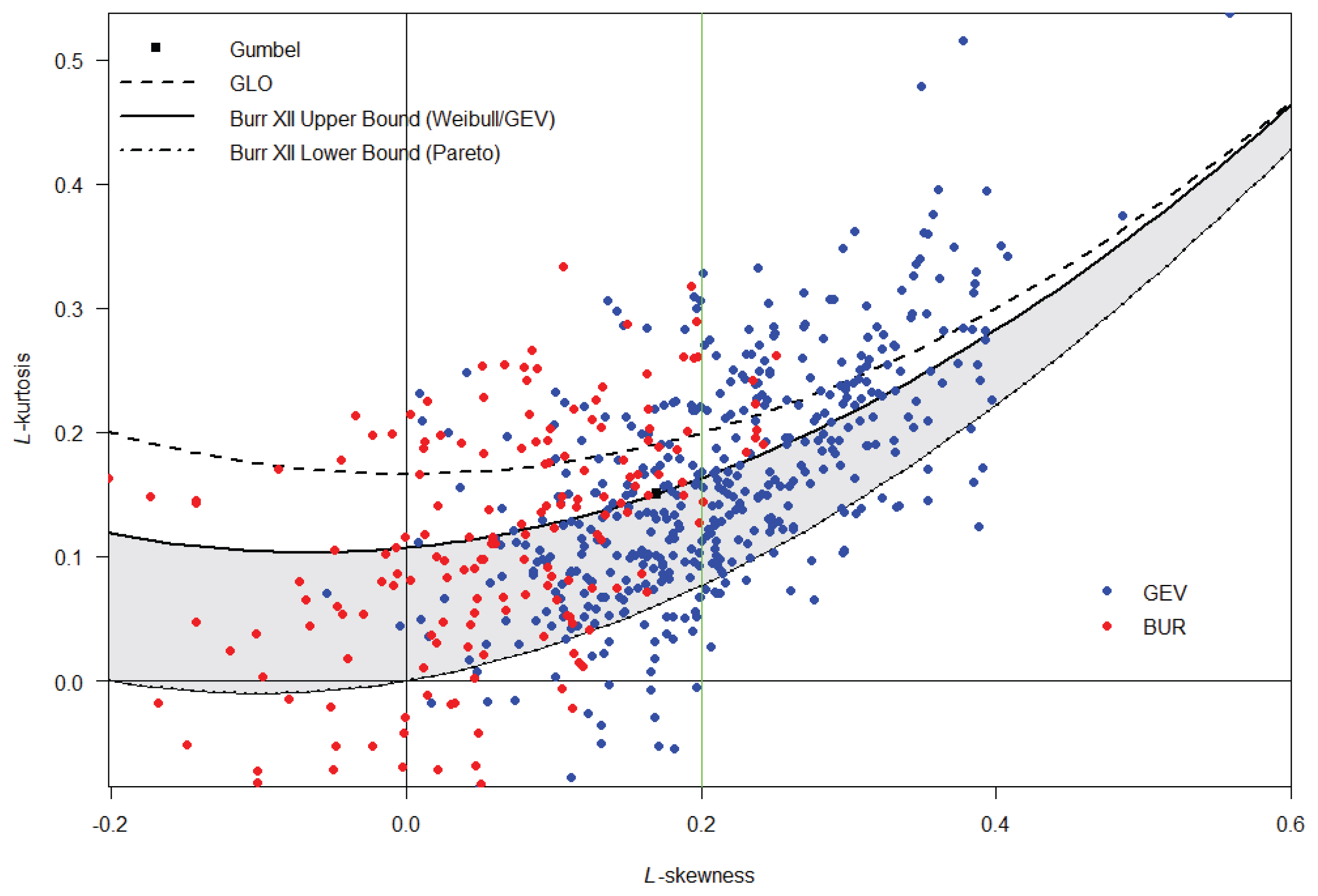
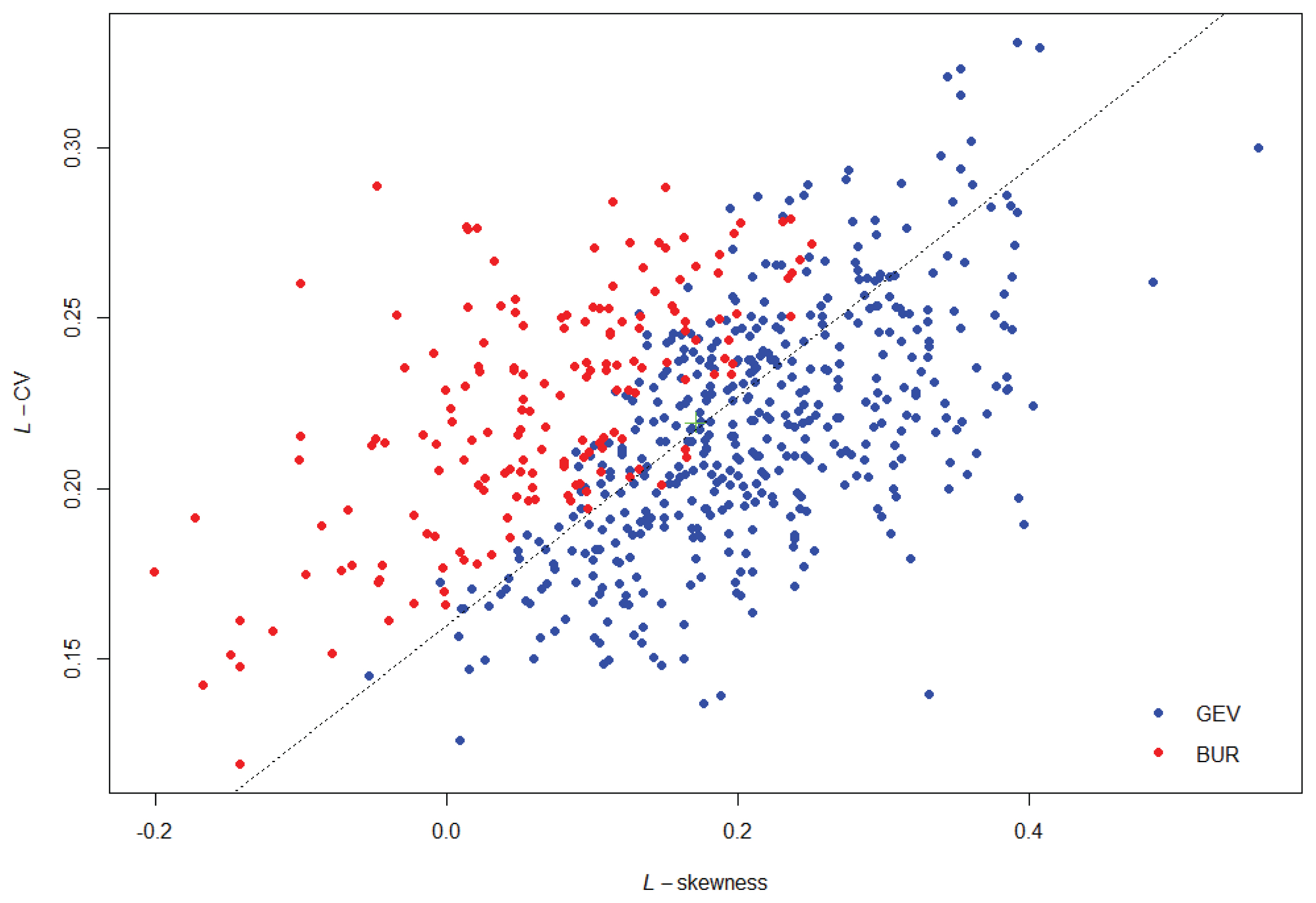
L-moment ratio diagram은 확률분포형별로 갖는 고유의 L-moment ratio와 주어진 표본 자료의 값을 비교하여 적정확률분포형을 선정하는 판단의 기준을 제공한다고 할 수 있다. Fig. 3은 617개 지점에 대하여 L-moment ratio (L-skewness, L-kurtosis)를 나타낸 그림으로 각 지점별로 채택된 분포형에 대하여 각각 파란색(GEV), 빨간색(BUR)으로 나타냈다. GEV 분포형은 L-skewness가 0.1보다 큰 경우 많은 지점에 적용가능하며, 적용한 분포형 중에서는 가장 우수하고 다양한 범위에서 적용이 가능한 것으로 판단된다. BUR 분포형은 2개의 형상매개변수로 구성되어 있어 적정한 범위가 영역으로 나타나며 주로 L-skewness가 0.2 이하인 경우에 많은 지점에 적용 가능한 것으로 판단된다.
Fig. 4는 L-moment ratio (L-CV, L-kurtosis)를 나타낸 그림으로 각 지점별로 1순위로 채택된 분포형은 Fig. 3과 동일하다. Fig. 3 보다는 좀 더 명확하게 분포형별로 적정범위가 나타나고 있다. L-skewness가 0.2보다 작은 범위에서는 L-CV값이 큰 경우 GEV 분포형보다 BURR 분포형이 채택될 가능성이 더 높은 것으로 판단된다.
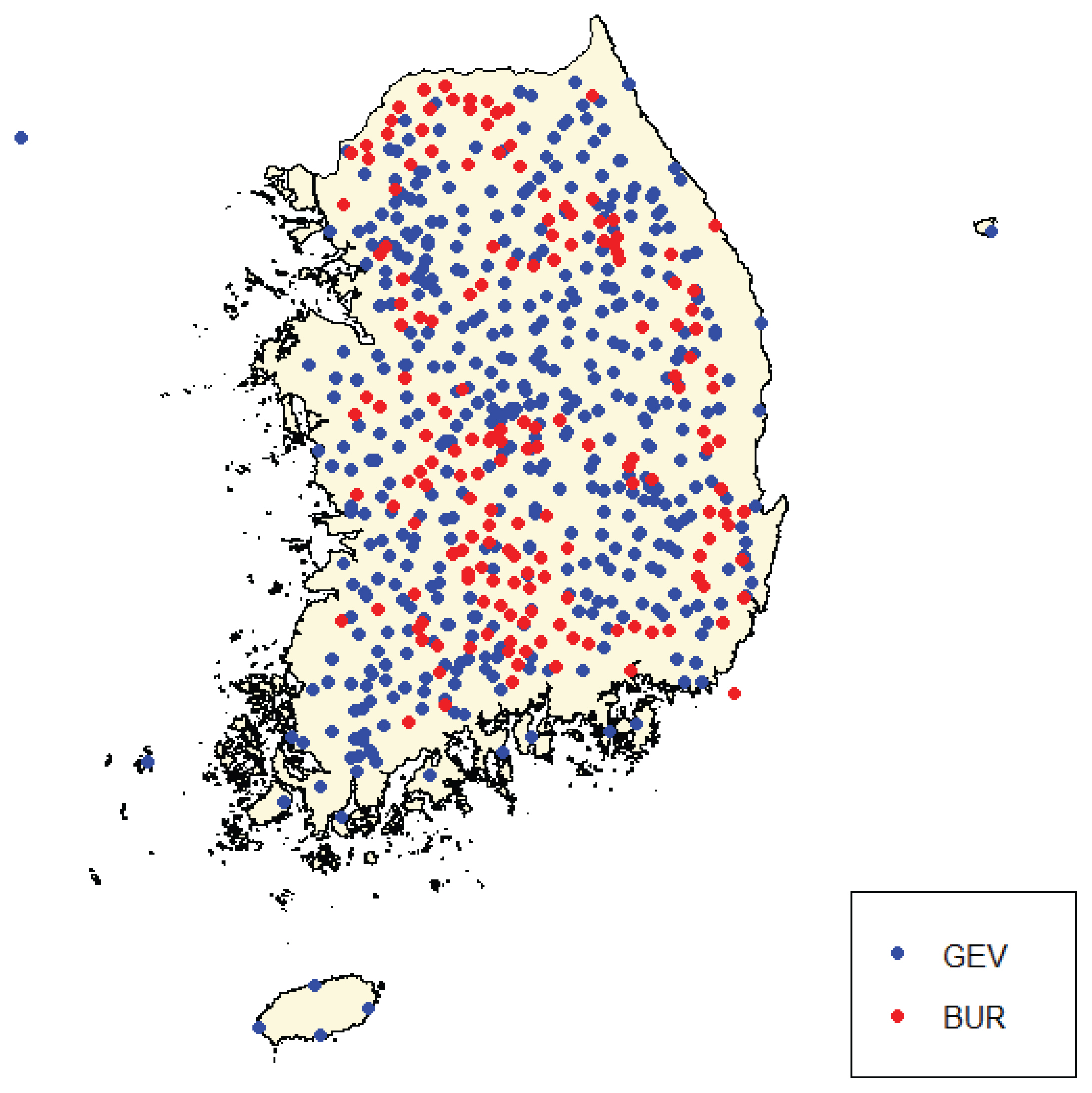
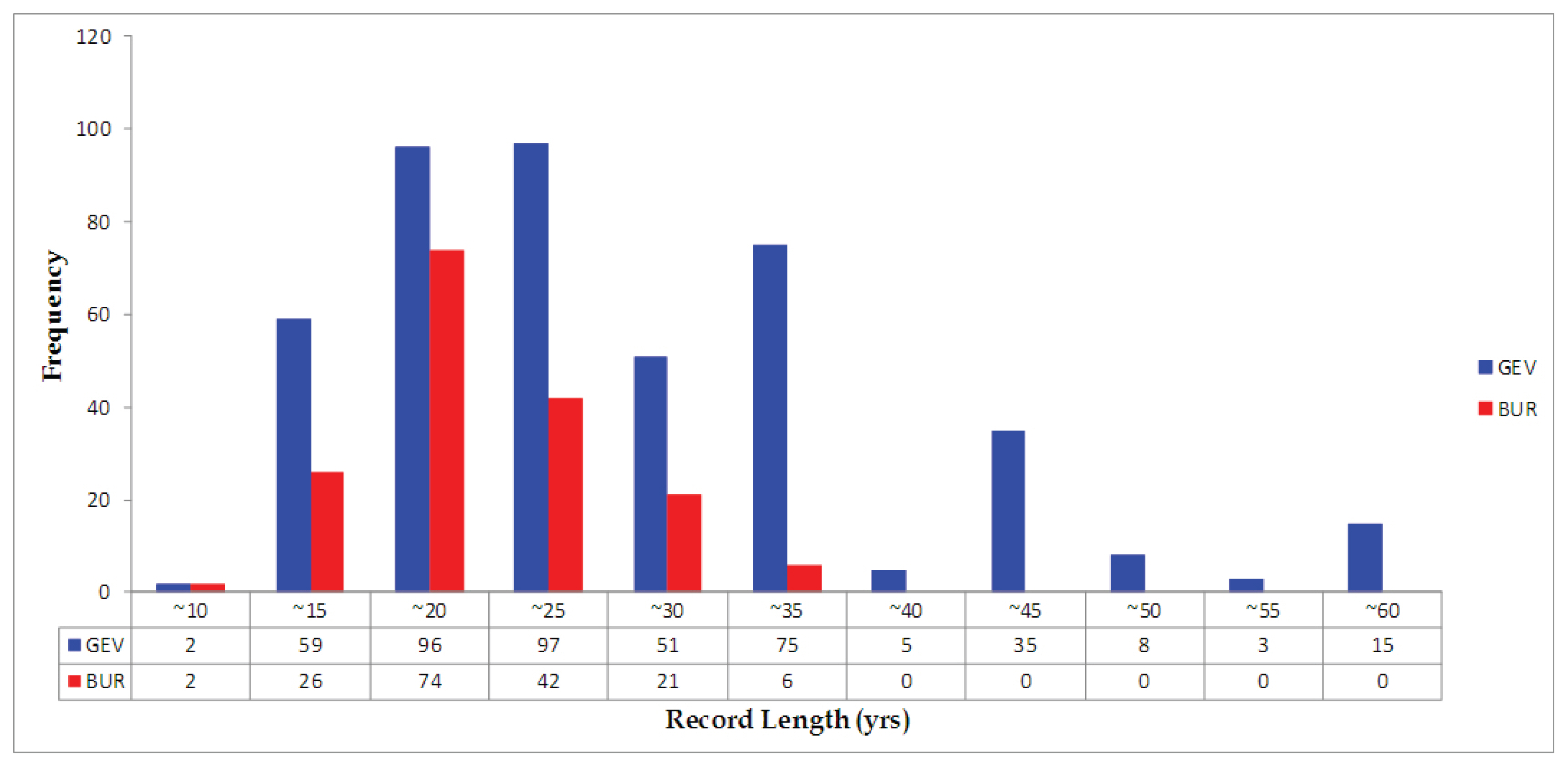
Fig. 5는 617개 지점에서 채택된 GEV, BUR 분포형을 지도상에 표기하여 나타내었다. GEV, BUR 분포형 모두 공간적으로 고르게 분포하였으며, 지점별로 적합하다고 선택된 분포형에 대한 공간적인 상관성은 적은 것으로 판단된다. 채택된 분포형에 대하여 각 지점별 자료년수의 빈도는 Fig. 6과 같이 나타났으며, 자료년수는 9년부터 57년까지 지점별로 다양하였다. 강우자료의 기간이 30년 이상인 147개 지점 중 141개 지점은 GEV 분포형이 더 적합하다고 나타났고, BUR 분포형을 채택한 6개 지점 중 가장 긴 자료기간은 35년이다. 즉, 자료기간이 긴 지점에서는 대체로 GEV 분포형이 적합한 것으로 나타났다.
4. 결 론
본 연구는 두 개의 형상매개변수를 가지고 있어 다양한 통계량을 유연하게 표현할 수 있다고 알려진 BUR 분포형을 우리나라 강우자료에 적용하여 사용 가능성을 살펴보고자 하였다. 우리나라 617개 지점을 대상으로 일반적으로 우리나라 강우자료에 적합하다고 알려진 GEV, GUM, GLO 분포 등과 함께 적합도 검정을 수행하였고, Monte Carlo 모의실험을 통하여 BUR 분포형의 적용 가능성을 정량적으로 평가하였다. 본 연구를 통하여 아래와 같은 결과를 얻을 수 있었다.
(1) 적용한 확률분포형에 대한 매개변수는 L-moment법을 이용하여 추정하였고 χ2-test와 K-S test 방법을 이용하여 적합도 검정을 수행하였다. 그 결과 GUM 분포형의 적합도 검정 통과율이 가장 낮게 나타났고, BUR 분포형은 GEV, GLO 분포형과 비교하여 큰 차이가 나지 않는 것으로 나타났다. 적합도 검정을 통과한 분포형별 검정통계량을 비교한 결과 GEV 분포형이 가장 많은 지점에서 작게 산정되었고, 적합도 검정 방법에 따라 BUR 분포형은 두 번째(K-S) 또는 세 번째(CS)로 작게 산정되었다.
(2) Monte Carlo 모의실험을 통하여 각 분포형의 log likelihood값을 비교한 결과 GEV 분포형이 가장 많은 지점에서 적절한 분포형으로 채택되었고, 그 뒤를 이어 BUR 분포형이 적절한 것으로 나타났다. 또한 BUR 분포형의 L-skewness 값이 0.2 이하이며 L-CV 값의 관계에 따라 적용 가능성이 커지며, 우수한 결과를 도출할 수 있을 것으로 판단된다.
(3) 각 지점별로 적합하다고 채택된 분포형을 공간적으로 검토한 결과 공간상관성은 적은 것으로 나타났고, 30년 이상의 긴 자료기간이 있는 지점에서는 GEV 분포형이 BUR 분포형 보다 적합한 것으로 나타났다.
(4) GUM, GEV, GLO 분포형은 우리나라 강우 자료에 비교적 적합하다고 알려져 있고, 널리 사용되고 있는 분포형이다. 본 연구에서 제시한 BUR 분포형은 기존의 다른 분포형과 함께 비교하여 우리나라 강우 자료의 빈도해석에 적용하는 데에는 문제가 없을 것으로 판단된다. 기존의 분포형이 적합하지 않은 지점에 대하여 BUR 분포형을 적용할 경우, 보다 적합한 확률수문량을 산정하는데 도움이 될 것으로 기대된다.
Acknowledgements
본 결과물은 환경부의 재원으로 한국환경산업기술원의 물관리 사업의 지원을 받아 연구되었습니다(과제번호 83081).