|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 19(3); 2019 > Article |
|
Abstract
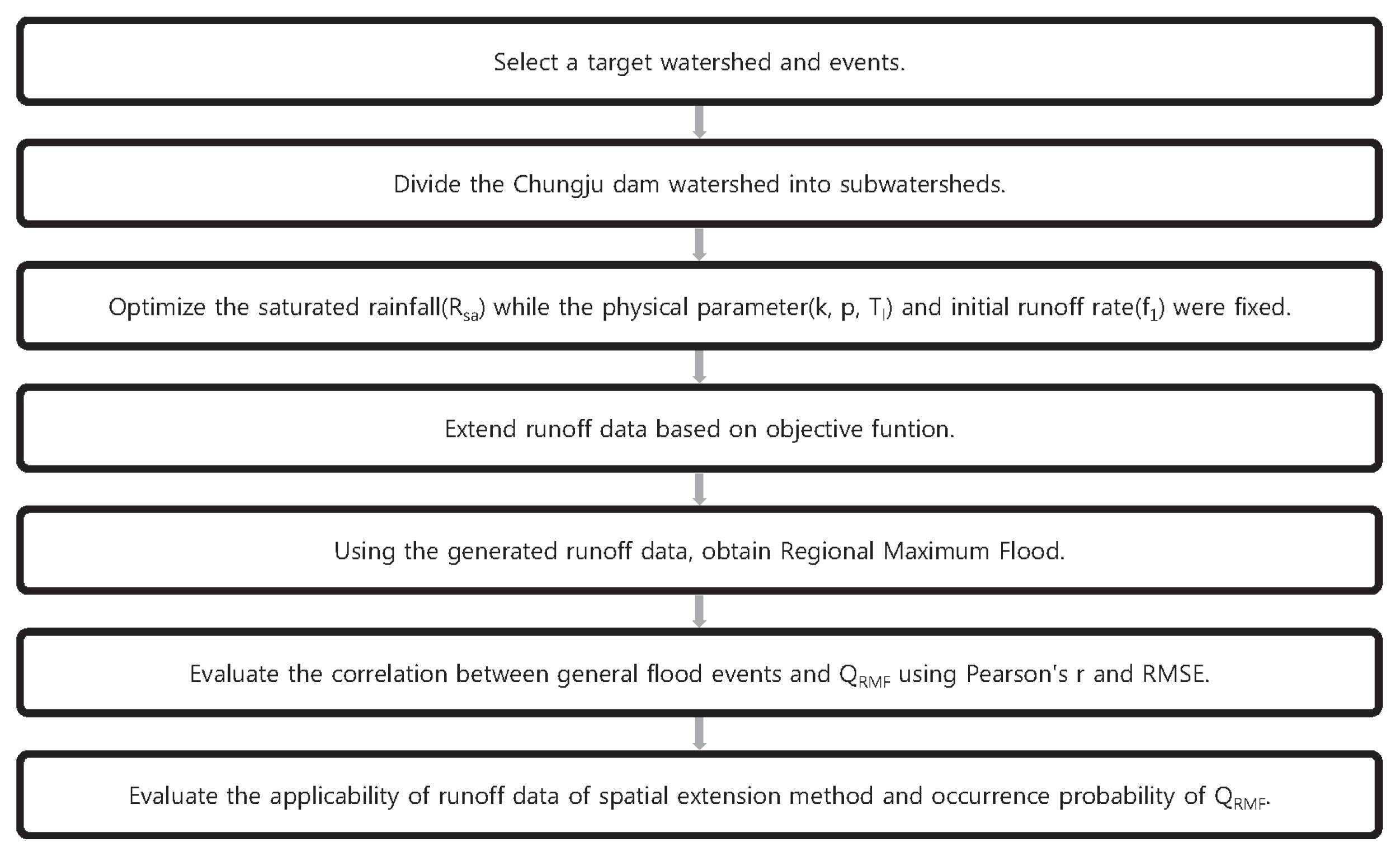
In this study, regional maximum floods for ungauged watersheds at the Choongju dam (CJD) were estimated using flood runoff data generated in storage function method (SFM) applications. The CJD watersheds were divided into smaller watersheds to generate runoff data for ungauged watersheds. The SFM optimized saturated rainfall (Rsa) while keeping other parameters (k, p, Tl, and f1) constant. Possible flood occurrences were estimated based on estimated runoff data and by analyzing the correlation between specific mean flooding events and regional maximum floods (QRMF) at the CJD. Results show that, in terms of being able to estimate runoff data for CJD watersheds, the spatial extension method based on an SFM was suitable for estimating possible regional flood occurrences (NSE > 0.5). Furthermore, there are strong correlations between flood events and QRMF (Pearson's r > 0.9); can be used to estimate regional maximum floods in the CJD watersheds.
ņÜöņ¦Ć
ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØä ļīĆņāüņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņŚÉ ļīĆĒĢ┤ ņĀĆļźśĒĢ©ņłśļ▓ĢņØä ĒÖ£ņÜ®ĒĢ£ ĒÖŹņłśņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØś ņĀüņÜ® Ļ░ĆļŖźņä▒ņØä ĒÅēĻ░ĆĒĢśĻ│Ā ņ¦ĆņŚŁņĄ£ļīĆĒÖŹņłśļ¤ēņØä ņČöņĀĢĒĢśņśĆļŗż. ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņé░ņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØä ņåīņ£ĀņŚŁņ£╝ļĪ£ ļČäĒĢĀĒĢ£ Ēøä ņåīņ£ĀņŚŁņØś ļ¼╝ļ”¼ņĀü ļ¦żĻ░£ļ│Ćņłś(k, p, Tl)ņÖĆ ņé¼ņāüņżæņŗ¼ ļ¦żĻ░£ļ│Ćņłś(f1, Rsa) ņżæ ļ¼╝ļ”¼ņĀü ļ¦żĻ░£ļ│Ćņłś(k, p, Tl)ņÖĆ ņ┤łĻĖ░ņ£ĀņČ£ņ£©(f1)ņØä Ļ│ĀņĀĢĒĢśņŚ¼ ĒżĒÖöņÜ░ļ¤ē(Rsa)ņØä ņĄ£ņĀüĒÖöĒĢśļŖö ņĀłņ░©ļź╝ ļ░¤ņĢśļŗż. ņé░ņĀĢĒĢ£ ņ£ĀņČ£ņ×ÉļŻīļź╝ ļ░öĒāĢņ£╝ļĪ£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņØ╝ļ░śņĀüņØĖ ĒÖŹņłśņé¼ņāüĻ│╝ ņ¦ĆņŚŁņĄ£ļīĆĒÖŹņłśļ¤ē(QRMF) ņé¼ņØ┤ņØś ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ ļČäņäØĒĢśņŚ¼ ņäĀņĀĢ ņ¦ĆņŚŁņØś ņĄ£ļīĆĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒĢśņśĆļŗż. ĻĘĖ Ļ▓░Ļ│╝ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻī ņČöņĀĢņŚÉ ņ׳ņ¢┤ņä£ ņĀĆļźśĒĢ©ņłśļ▓Ģ ĻĖ░ļ░śņØś ĒÖŹņłśņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØĆ ņ¦ĆņŚŁļ░£ņāØĻ░ĆļŖź ĒÖŹņłśņé¼ņāü ņČöņĀĢņŚÉ ļīĆĒĢ┤ņä£ ņĀüĒĢ®ĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż(NSE>0.5). ļśÉĒĢ£, ņé░ņĀĢĒĢ£ ņ£ĀņČ£ņ×ÉļŻīņØś ņØ╝ļ░śņĀüņØĖ ĒÖŹņłśņé¼ņāüĻ│╝ QRMFņé¼ņØ┤ņØś ņāüĻ┤ĆĻ┤ĆĻ│äĻ░Ć ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ņ£╝ļ®░ (PearsonŌĆÖs r>0.9), ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņ¦ĆņŚŁņĄ£ļīĆĒÖŹņłśļ¤ēņØä ņČöņĀĢĒĢĀ ņłś ņ׳ņŚłļŗż.
ĻĖ░Ēøäļ│ĆĒÖöļĪ£ ņØĖĒĢ┤ ņĀä ņäĖĻ│äņĀüņ£╝ļĪ£ ĻĖ░ņāüņØ┤ļ│ĆĒśäņāüņØ┤ ļ¦ÄņØ┤ ļ░£ņāØĒĢśĻ│Ā ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĻĖ░ņāüņØ┤ļ│ĆĒśäņāüņØĆ ĒśĖņÜ░ Ēī©Ēä┤ņØś ļ│ĆĒÖö ļ░Å ĻĄŁņ¦Ćņä▒ ĒśĖņÜ░ņØś ņ”ØĻ░ĆļĪ£ ļéśĒāĆļéśĻ│Ā ņ׳ņ£╝ļ®░, ĒÖŹņłś ļō▒ ņ×ÉņŚ░ņ×¼ĒĢ┤ņØś ņ”ØĻ░ĆļĪ£ ņØ┤ņ¢┤ņĀĖ ņłśņ×ÉņøÉņŚÉ Ēü░ Ēö╝ĒĢ┤ļź╝ ņŻ╝Ļ│Ā ņ׳ļŗż(Park et al., 2004). ņĢäņÜĖļ¤¼ ļ¼Ėļ¬ģņØ┤ ļ░£ļŗ¼ĒĢ©ņŚÉ ļö░ļØ╝ ļīĆĻĘ£ļ¬© Ēöīļ×£ĒŖĖņé¼ņŚģ, ĒåĀņ¢æ ĒżņןĻ│Ąņé¼, ļÅäņŗ£ĒÖö ļō▒ ĒåĀņ¦Ć ņØ┤ņÜ®ņØ┤ ĒÖĢļīĆļÉśņ¢┤ ĒåĀņ¦ĆņØś Ēæ£ļ®┤ ņĪ░ļÅäĻ│äņłśņÖĆ Ēł¼ņłśņ£©ņØ┤ Ļ░ÉņåīĒĢśĻ│Ā ņ׳ņ£╝ļ®░, ņØ┤ļĪ£ ņØĖĒĢśņŚ¼ ņŗØņāØ ļČäĒżņØś Ļ░Éņåī ļ░Å ĒĢśņ▓£ņØś ņ¦üņäĀĒÖöļĪ£ Ļ░ĢņÜ░Ļ░Ć ņ£ĀņČ£ ņČ£ĻĄ¼ ņ¦ĆņĀÉĻ╣īņ¦Ć ļÅäļŗ¼ĒĢśļŖö ņŗ£Ļ░äņØ┤ ņ¦¦ņĢäņ¦ĆĻ│Ā ĒÖŹņłśļ░®ņ¢┤ļŖźļĀźņØ┤ Ļ░ÉņåīĒĢśņŚ¼ ĒÖŹņłśĒö╝ĒĢ┤Ļ░Ć ņ”ØĻ░ĆĒĢśņśĆļŗż(Kwon et al., 2014). ĻĄŁļé┤ņŚÉņä£ļŖö 1997ļģä ņØ┤ĒøäļĪ£ ĻĄŁņ¦Ćņä▒ ĒśĖņÜ░ļĪ£ ņØĖĒĢ£ Ēö╝ĒĢ┤ļ¤ē ļ░Å ĒÖŹņłśļ¤ē ĻĘ£ļ¬©ņØś ņ”ØĻ░ĆļĪ£ ĻĖ░ņĪ┤ ņłśĻ│ĄĻĄ¼ņĪ░ļ¼╝ņØä ņ£äĒśæĒĢśļŖö ņłśņżĆņŚÉ ņØ┤ļź┤ļĀĆļŗż. ņØ┤ ļĢīļ¼ĖņŚÉ ņłśĻ│ĄĻĄ¼ņĪ░ļ¼╝ņØ┤ ĒÖŹņłśļĪ£ ņåÉņāüļÉśĻ▒░ļéś ļČĢĻ┤┤ļÉśņ¦Ć ņĢŖļÅäļĪØ ņĀüņĀłĒĢ£ ļīĆņ▒ģņØä ļ¦łļĀ©ĒĢ┤ņĢ╝ ĒĢ£ļŗżļŖö ņŻ╝ņןņØ┤ ņØ╝Ļ│Ā ņ׳ļŗż(Tofiq and Guven, 2014). ļśÉĒĢ£, ĻĖ░ņĪ┤ ņłśĻ│ĄĻĄ¼ņĪ░ļ¼╝Ļ│╝ ņŗĀĻĘ£ ņłśĻ│ĄĻĄ¼ņĪ░ļ¼╝ņØś ņĢłņĀĢņä▒ņØä ĒÖĢļ│┤ĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņ▓©ļæÉņ£Āļ¤ēņŚÉ Ļ┤ĆĒĢ£ ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ĒÖŹņłśĻĘ£ļ¬©ļź╝ ņČöņĀĢĒĢśņŚ¼ ņłśĻ│ĄĻĄ¼ņĪ░ļ¼╝ļōżņØś ņäżĻ│äļ╣łļÅäļź╝ ņāłļĪŁĻ▓ī ņĀ£ņŗ£ĒĢ┤ņĢ╝ ĒĢ£ļŗżļŖö ņŻ╝ņןļÅä ņĀ£ĻĖ░ļÉśņŚłļŗż(Korea River Association, 2016).
ņØ╝ļ░śņĀüņ£╝ļĪ£ ņäżĻ│äĒÖŹņłśļ¤ē ņé░ņĀĢņŚÉļŖö ĒÖŹņłśļ¤ē ņ×ÉļŻīņØś ņŗ£Ļ│äņŚ┤ ļ╣łļÅäĒĢ┤ņäØ ļ░®ļ▓Ģ(Flood Frequency Analysis, FFA)Ļ│╝ ņäżĻ│ä Ļ░ĢņÜ░ŌĆÉņ£ĀņČ£ Ļ┤ĆĻ│äļČäņäØ ļ░®ļ▓Ģ(Design Rainfall Runoff Analysis, DRRA)ņØä ņé¼ņÜ®ĒĢ£ļŗż(Chae et al., 2018). ĒĢśņ¦Ćļ¦ī ļæÉ Ļ░Ćņ¦Ć ļ¬©ļæÉ ņŗżņĖĪ ĒÖŹņłśļ¤ē ņ×ÉļŻīļź╝ ĻĖ░ļ░śņ£╝ļĪ£ ņłśņ£äŌĆÉņ£Āļ¤ē Ļ┤ĆĻ│ä Ļ│ĪņäĀ ļČäņäØ ļ░Å ņ£ĀņČ£ļ¤ē ļ¬©ņØśļź╝ ņŗżĒ¢ēĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņåīĒĢśņ▓£ņØ┤ļéś ņ£ĀņČ£ ņĖĪņĀĢņØ┤ ņØ┤ļŻ©ņ¢┤ņ¦ĆĻ│Ā ņ׳ņ¦Ć ņĢŖņØĆ Ļ││ņŚÉņä£ļŖö ņĀüņÜ®ĒĢśĻĖ░ ĒלļōĀ ņŗżņĀĢņØ┤ļŗż(Ministry of Land, Transport and Maritime Affairs, 2012). ņØ┤ņ▓śļ¤╝ Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīĻ░Ć ļČĆņĪ▒ĒĢśĻ▒░ļéś Ļ▓Ćņ”ØļÉśņ¦Ć ņĢŖņØĆ ņ£ĀņŚŁņØä ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØ┤ļØ╝Ļ│Ā ĒĢ£ļŗż(Sivapalan et al., 2003). ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻī ĒÖĢļ│┤ļŖö ņäżĻ│äĒÖŹņłśļ¤ē ļČäņäØņŚÉ ņ׳ņ¢┤ņä£ ņżæņÜöĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ Ēśäņ×¼ ņĀĢĒÖĢĒĢśĻ│Ā ņŗĀļó░ļÅä ņ׳ļŖö ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ĒÖĢļ│┤ĒĢśĻĖ░ ņ£äĒĢ£ ņŚ░ĻĄ¼ļŖö ĻŠĖņżĆĒ׳ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ĒåĄĻ│äņĀüņ£╝ļĪ£ ņé░ņĀĢĒĢśļŖö ļŗżņżæņäĀĒśĢĒÜīĻĘĆļČäņäØ(Vogel et al., 1999; Goswami et al., 2007)ņØä ņŻ╝ļĪ£ ņé¼ņÜ®ĒĢśņśĆņ£╝ļ®░, ņĄ£ĻĘ╝ņŚÉļŖö ņ¦ĆņŚŁĒÜīĻĘĆļ¬©ĒśĢņØś ņäżļ¬ģļ│ĆņłśņŚÉ ņłśļ¼Ėļ¬©ĒśĢņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöĻ░ĆĒĢśņŚ¼ ĒÜīĻĘĆļ¬©ĒśĢņØś ņĀüĒĢ®ņä▒ņØä Ē¢źņāüĒĢ£ ĒĢśņØ┤ļĖīļ”¼ļō£ ņ¦ĆņŚŁĒÖö ļ¬©ĒśĢņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśĻĖ░ļÅä ĒĢśņśĆļŗż(Kim et al., 2018). ļśÉĒĢ£, ļ»ĖĻ│äņĖĪņ£ĀņŚŁ ļé┤ņŚÉ ĒĢśļźś ņ¦ĆņĀÉņØä ņżæņŗ¼ņ£╝ļĪ£ ņĀäņ▓┤ņ£ĀņŚŁņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöņĀĢĒĢśņŚ¼ ĒÖŹņłśņ£ĀņČ£ņØä ļ¬©ņØśĒĢśņśĆņ£╝ļ®░(Bae and Chung, 2000), ņØ┤ļź╝ ņØæņÜ®ĒĢśņŚ¼ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØä ņåīĻĘ£ļ¬©ļĪ£ ļČäĒĢĀĒĢ£ ļÆż Ļ░ü ņåīņ£ĀņŚŁņØś ņ£ĀņČ£ ņČ£ĻĄ¼ ņ¦ĆņĀÉ ņżæņŗ¼ņ£╝ļĪ£ ļ¦żĻ░£ļ│Ćņłśļź╝ ņé░ņĀĢĒĢśņŚ¼ ņ£ĀņČ£ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśĻĖ░ļÅä ĒĢśņśĆļŗż(Kim et al., 2013). ļČäĒżĒśĢ ļ¬©ĒśĢĻ│╝ Ļ│ĄĻ░äĒÖĢņןņ×ÉļŻī ņāØņä▒ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ĒÖŹņłśņ£ĀņČ£ ņŗ£Ļ│äņŚ┤ ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśņŚ¼ ņ▓©ļæÉņ£Āļ¤ēņØä ņČöņČ£ĒĢśĻ│Ā ļČäņäØĒĢ£ ņŚ░ĻĄ¼ļÅä ņ׳ļŗż(Kim and Shin, 2017).
ĻĖ░ņĪ┤ ņŚ░ĻĄ¼ļź╝ ļ│┤ļ®┤ ĒÖŹņłśļ¤ē ņé░ņĀĢ ļ░Å ĒÖŹņłśĒĢ┤ņäØņŚÉ ņ׳ņ¢┤ņä£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś Ļ░ĢņÜ░ Ļ│ĄĻ░äļČäĒżļź╝ Ļ│ĀļĀżĒĢ£ ņ£Āļ¤ēņé░ņČ£ņØ┤ ĒĢäņłśņĀüņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ĒÖŹņłśņ×ÉļŻīļź╝ ņČöņČ£ĒĢśĻĖ░ ņ£äĒĢ┤ņä£ ņ£ĀņŚŁņØś ņłśļ¼ĖĒśäņāü ņśłņĖĪĻ│╝ ļ¦żĻ░£ļ│Ćņłśļź╝ ņĄ£ņĀüĒÖöĒĢśļŖö ņĀłņ░©Ļ░Ć ņÜöĻĄ¼ļÉ£ļŗż. ņØ┤ņŚÉ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņŚÉ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢśņŚ¼ ņé░ņČ£ĒĢ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīĻ░Ć Ļ│ĄĻ░äņĀüņØĖ ļČäņäØ Ļ░ĆļŖźņä▒ņØ┤ ņ׳ļŖöņ¦Ć ĒÖĢņØĖĒĢśĻ│Āņ×É ĒĢ£ļŗż. ļśÉĒĢ£, ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņØ╝ļ░śņĀüņØĖ ĒÖŹņłś ņé¼ņāüĻ│╝ KovacsĻ░Ć ņĀ£ņĢłĒĢ£ QRMF ņé¼ņØ┤ņØś ņāüĻ┤ĆĻ┤ĆĻ│ä ļČäņäØĒĢśņŚ¼ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØä ĒżĒĢ©ĒĢ£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņŚÉ ļīĆĒĢ£ ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØś ņČöņĀĢņØä Ļ▓ĆĒåĀĒĢśļŖö ļŹ░ ļ¬®ņĀüņØä ļæÉņŚłļŗż.
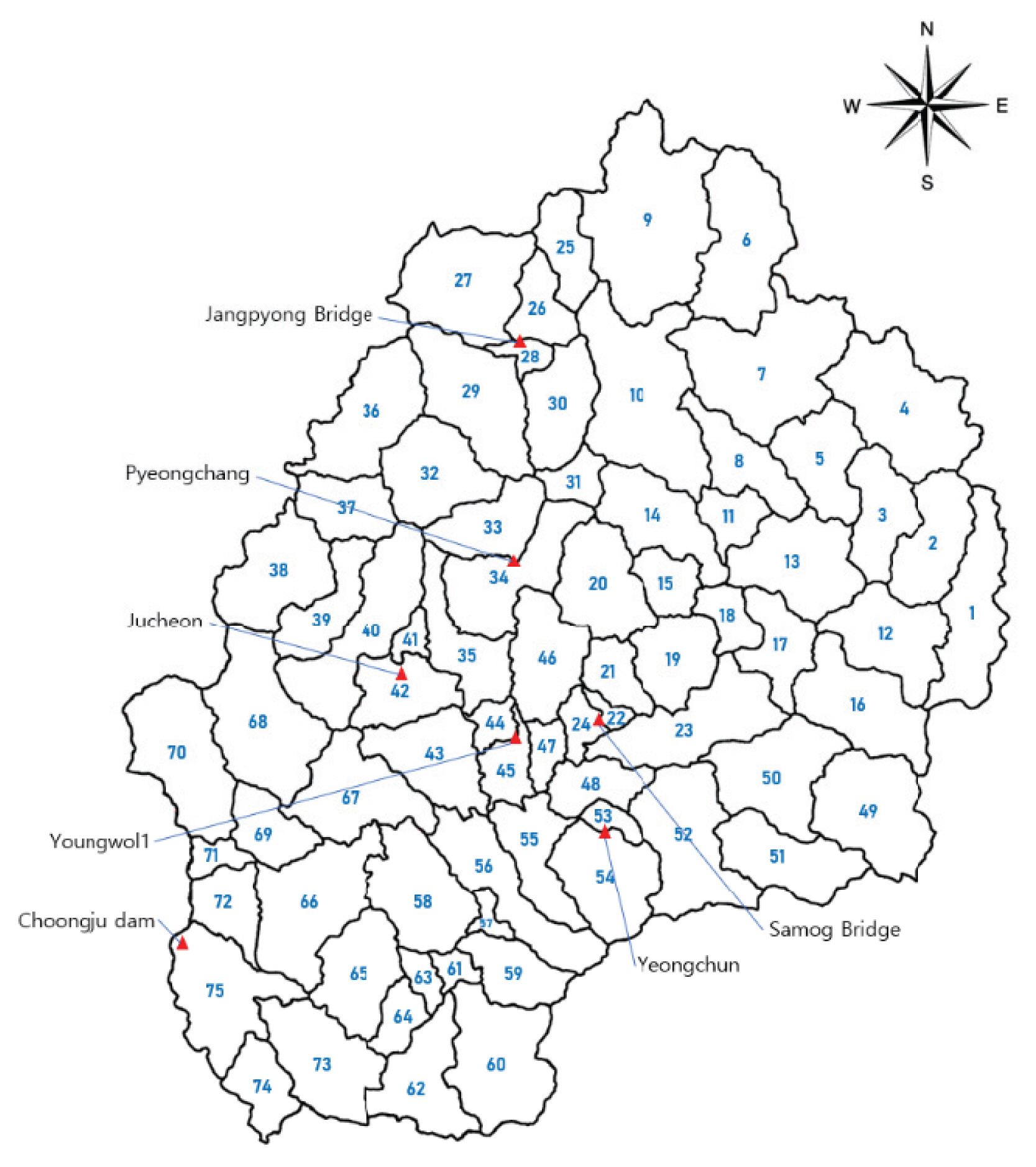
ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻī ņé░ņČ£Ļ│╝ ĒÖŹņłś ņé¼ņāü ļČäņäØņØä ņ£äĒĢ┤ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØä ļīĆņāü ņ£ĀņŚŁņ£╝ļĪ£ ņäĀņĀĢĒĢśņśĆļŗż. ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØĆ ļīĆĒĢ£ļ»╝ĻĄŁ Ļ░ĢņøÉļÅä ļé©ĒĢ£Ļ░Ģ ņłśĻ│äņŚÉ ņ׳ņ£╝ļ®░, ņāØĒÖ£ŌŗģļåŹņŚģŌŗģĻ│ĄņŚģņÜ®ņłś Ļ│ĄĻĖē, ļ░£ņĀä, ĒÖŹņłśņĪ░ņĀł ļō▒ņØś ņżæņÜöĒĢ£ ņŚŁĒĢĀņØä ĒĢśļŖö ĻĄŁļé┤ ņĄ£ļīĆ ĻĘ£ļ¬©ņØś ļŗżļ¬®ņĀüļīÉņØ┤ļŗż. ņČ®ņŻ╝ļīÉņØĆ ņ£ĀņŚŁļ®┤ņĀü 6,648k m2, ņ┤ØņĀĆņłśņÜ®ļ¤ē 27ņ¢Ą m3ņØ┤Ļ│Ā 6.16ņ¢Ą m3ņØś ĒÖŹņłśļź╝ ņĪ░ņĀłĒĢĀ ņłś ņ׳ļŗż. ņ£ĀļĪ£ ņŚ░ņן 375 kmņŚÉ ļŗ¼ĒĢśļŖö ļīĆĒĢśņ▓£ņØĆ ņä£ņÜĖ ļÅÖņ¬Į ņĢĮ 20 km ņ¦ĆņĀÉņŚÉņä£ ļČüĒĢ£Ļ░ĢĻ│╝ ĒĢ®ļźśĒĢśņŚ¼ ĒĢ£Ļ░Ģļ│Ėļźśļź╝ ĒśĢņä▒ĒĢ£ļŗż(KŌĆÉwater, 2012).
Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīļŖö 1985ļģäļČĆĒä░ ņĪ┤ņ×¼ĒĢśļéś ņ£ĀņČ£ņ×ÉļŻīņØś Ļ│ĄĻ░ä ĒÖĢņן Ļ░ĆļŖźņä▒ņØä ļ│┤ĻĖ░ ņ£äĒĢ┤ Table 1Ļ│╝ Ļ░ÖņØ┤ 2008~2013ļģä, 2016~2017ļģäņØä ņäĀņĀĢĒĢśņśĆļŗż. ņäĀņĀĢĒĢ£ ņŚ░ļÅäņŚÉņä£ ņŚ░ Ļ░Ģņłśļ¤ēņØ┤ Ļ░Ćņן ļ¦Äņ£╝ļ®░ ĒÖŹņłśļ¤ē ņ×ÉļŻīĻ░Ć ņĀüņĀłĒĢśĻ▓ī Ēæ£ĒśäļÉ£ ĻĖ░Ļ░ä(ĒÖŹņłśņØś ņŗ£ņ×æĻ│╝ ļüØņØä ļ¬ģĒÖĢĒ׳ ĻĄ¼ļ│äĒĢĀ ņłś ņ׳ļŖö)ņØä ļīĆņāü ĻĖ░Ļ░äņ£╝ļĪ£ ņäĀņĀĢĒĢśņśĆņ£╝ļ®░, 1ņŗ£Ļ░ä ļŗ©ņ£äņØś Ļ░Ģņłśļ¤ēņ×ÉļŻīņÖĆ ņ£ĀņČ£ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ļ┤ĆņĖĪĒÖŹņłś ņé¼ņāüĻ│╝ ļ¬©ņØśĒÖŹņłś ņé¼ņāüņØä ļ╣äĻĄÉ ļ░Å ļČäņäØĒĢśņśĆļŗż. ņĄ£ĻĘ╝ ņé¼ņāüņŚÉ Ļ░ĆĻ╣īņøīņ¦łņłśļĪØ ņłśņ£äĻ┤ĆņĖĪņåīĻ░Ć ņ”ØĻ░ĆĒĢśņśĆļŖöļŹ░ ņłśņ£äĻ┤ĆņĖĪņåīņØś Ļ░£ņłśņŚÉ ļö░ļØ╝ ņ£ĀņŚŁ ĒŖ╣ņä▒ņØ┤ ļŗ¼ļØ╝ņ¦Ćļ»ĆļĪ£ ļÅÖņØ╝ĒĢ£ ņ£ĀņŚŁ ĒŖ╣ņä▒ņØä Ļ░Ćņ¦ä ņŚ░ļÅäļź╝ ņäĀņĀĢĒĢśņŚ¼ 2008~2009ļģä 22Ļ░£, 2010~2013ļģä 35Ļ░£, 2016~2017ļģä 75Ļ░£ļĪ£ ņ£ĀņŚŁņØä ļČäĒĢĀĒĢśņśĆļŗż. ļśÉĒĢ£, ņĀüņĀłĒĢ£ ļ╣äĻĄÉņÖĆ Ļ▓Ćņ”ØņØś ĒåĄņØ╝ņä▒ņØä ņ£äĒĢ┤ ņČ®ņŻ╝ļīÉ, ņśüņøö1, ņśüņČś ņłśņ£äĻ┤ĆņĖĪņåīļź╝ Ļ▓Ćņ”Øņ¦ĆņĀÉņ£╝ļĪ£ ņ¦ĆņĀĢĒĢśņśĆļŗż(Fig. 1).
ņ¦ĆĒæ£ļ®┤ņŚÉ ļé┤ļ”░ Ļ░ĢņÜ░ļŖö ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£, ņżæĻ░äņ£ĀņČ£, ņ¦ĆĒĢśņłśņ£ĀņČ£ļĪ£ ļéśļēśņ¢┤ ņ£ĀņŚŁ ņČ£ĻĄ¼ ņ¦ĆņĀÉĻ╣īņ¦Ć ĒØśļ¤¼Ļ░äļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ ļīĆĒĢ┤ņä£ ņ£ĀņČ£ĒĢ┤ņäØņØä ņŗ£Ē¢ēĒĢśļ®░ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņØĆ ņŚ¼ļ¤¼ Ļ░Ćņ¦Ć ņØĖņ×ÉņŚÉ ņØśĒĢ┤ ņśüĒ¢źņØä ļ░øļŖöļŗż. ņśüĒ¢źņØä ņŻ╝ļŖö ņØĖņ×ÉļŖö ņłśļ¼ĖĒĢÖņĀü Ļ┤ĆņĀÉņ£╝ļĪ£ ĻĖ░ĒøäĒĢÖņĀü ņØĖņ×ÉņÖĆ ņ¦ĆĒśĢĒĢÖņĀü ņØĖņ×ÉļĪ£ ļČäļźśĒĢĀ ņłś ņ׳ļŗż. ĻĖ░ĒøäĒĢÖņĀü ņØĖņ×ÉļŖö Ļ░ĢņÜ░, ņ”Øļ░£, Ļ░ĢņÜ░ Ļ░ĢļÅä, Ļ░ĢņÜ░ ņ¦ĆņåŹņŗ£Ļ░ä ļō▒ņØä ņØśļ»ĖĒĢśļ®░ ņ¦ĆĒśĢĒĢÖņĀü ņØĖņ×ÉļŖö ņ£ĀņŚŁļ®┤ņĀü, ņ£ĀņŚŁņØś ļ░®Ē¢źņä▒(Ļ░ĢņÜ░ļČäĒż), ņ£ĀņŚŁņØś ĒśĢņāü, Ēł¼ņłśļŖź ļō▒ņØä ņØśļ»ĖĒĢ£ļŗż. Singh (1997)ņØĆ ņØ┤ļ¤¼ĒĢ£ ņØĖņ×ÉņØś Ļ│ĄĻ░äļČäĒżĻ░Ć ņ£ĀņČ£ņŚÉ Ēü░ ņśüĒ¢źņØä ļ»Ėņ╣śļŖö Ļ▓āņØä ļ░ØĒśĆļāłļŗż. Ļ░ĢņÜ░ņØś ņØ┤ļÅÖ ļ░®Ē¢źņØ┤ ņ£ĀņČ£ņØś ĒØÉļ”ä ļ░®Ē¢źĻ│╝ Ļ░ÖņØä ļĢī ņĄ£ļīĆ ņ▓©ļæÉņ£Āļ¤ēņØ┤ ļ░£ņāØĒĢśņśĆĻ│Ā, ņØ╝ņĀĢĒĢ£ Ļ░ĢņÜ░ Ēī©Ēä┤ļ│┤ļŗż ļ│ĆļÅÖĒĢśļŖö Ļ░ĢņÜ░ Ēī©Ēä┤ņŚÉņä£ ļŹö ļ¦ÄņØĆ ņ▓©ļæÉņ£Āļ¤ēņØ┤ ļ░£ņāØĒĢśņśĆļŗż. ņØ┤Ļ▓āņØĆ Ļ░ĢņÜ░ņØś Ļ│ĄĻ░äņĀüņØĖ ļČäĒżĻ░Ć ņ£ĀņČ£ņŚÉ ņāüļŗ╣ĒĢ£ ņśüĒ¢źņØä ļ»Ėņ╣śļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż. Nassif and Wilson (1975)ņØĆ ņ╣©Ēł¼ļŖź ļ░Å ņé¼ļ®┤ Ļ▓Įņé¼ņÖĆ ņ£ĀņČ£ ņé¼ņØ┤ņØś Ļ┤ĆĻ│äļź╝ ļČäņäØĒĢśņśĆļŗż. ņ£ĀņČ£ņØĆ ņŗØņāØņØ┤ ļČäĒżļÉ£ ĒåĀņ¦Ćļ│┤ļŗż ĻĘĖļĀćņ¦Ć ņĢŖņØĆ ĒåĀņ¦ĆņŚÉņä£ ļŹö ļ¦ÄĻ▓ī ļéśĒāĆļé¼ņ£╝ļ®░, ņé¼ļ®┤Ļ▓Įņé¼Ļ░Ć ĻĖēĒĢĀņłśļĪØ ņ£ĀņČ£ņØ┤ ļ¦ÄņĢäņ¦ĆļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ĒŖ╣Ē׳ ņ¦ĆĒĢśņłś ĒĢ©ņ¢æļźĀņØś Ļ│ĄĻ░äņĀüņØĖ ļČäĒżļŖö ņ£ĀņČ£ņŚÉ ļīĆĒĢ┤ ņ¦Ćļ░░ņĀüņØĖ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż(Singh, 1997). ņØ┤Ļ▓āņØĆ ņ╣©Ēł¼ļŖź, ņé¼ļ®┤ Ļ▓Įņé¼, ĻĖ░ņĀĆ ņ£Āļ¤ē ļō▒Ļ│╝ Ļ░ÖņØĆ ņØĖņ×ÉņØś Ļ│ĄĻ░äņĀüņØĖ ļČäĒżņŚÉ ļö░ļØ╝ ņ£ĀņČ£ņØ┤ ļ│ĆĒÖöĒĢśļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż. ņ£ĀņČ£ņ×ÉļŻīņØś ņé░ņĀĢ ļ░Å ļČäņäØņØä ĒĢśļŖö ļŹ░ ņ׳ņ¢┤ņä£ ņ£ĀņČ£ņØĆ ņ£ĀĒÜ©ņÜ░ļ¤ēĻ│╝ ļ¦żņÜ░ ļ░ĆņĀæĒĢ£ Ļ┤ĆļĀ©ņØ┤ ņ׳ņ£╝ļ»ĆļĪ£ ņ£ĀņČ£ņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ņØĖņ×ÉņŚÉ ļīĆĒĢ£ Ļ│ĄĻ░äņĀüņØĖ ĒĢ┤ņäØņØĆ ļ¦żņÜ░ ņżæņÜöĒĢśļŗż. ļö░ļØ╝ņä£ ņ£ĀņČ£ņ×ÉļŻīļź╝ Ļ│ĄĻ░äĒÖĢņןĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņ£ĀĒÜ©ņÜ░ļ¤ēņØä ļ¦żĻ░£ļ│ĆņłśļĪ£ ņäżņĀĢĒĢśņŚ¼ ņĄ£ņĀüĒÖöĒĢśļŖö Ļ│╝ņĀĢņØ┤ ĒĢäņÜöĒĢśļŗż.
ņĀĆļźśĒĢ©ņłśļ¬©ĒśĢ(Storage Function Method, SFM)ņØĆ Ļ░ĢņÜ░ŌĆÉņ£ĀņČ£ņØś ļ╣äņäĀĒśĢņä▒Ļ│╝ ņ×ÉņŚ░ņāüĒā£ņŚÉņä£ ļ░£ņāØĒĢśļŖö ĒÖŹņłśņ£ĀņČ£ņØś ļČĆņĀĢļźśļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ĒĢ┤ņäØĒĢĀ ņłś ņ׳ļŗż. ļö░ļØ╝ņä£ ņé░ņ¦ĆĻ░Ć ļ¦ÄņØĆ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņŚÉ ļīĆĒĢ┤ ņĀĆļźśĒĢ©ņłśļ¬©ĒśĢņØä ņĀüņÜ®ĒĢśņśĆļŗż. ņĀĆļźśĒĢ©ņłśļ¬©ĒśĢņØĆ ņ£ĀņŚŁņØś ņĀĆļźśļ░®ņĀĢņŗØĻ│╝ ĒĢśļÅäņØś ņĀĆļźśļ░®ņĀĢņŗØņŚÉ ĻĖ░ņ┤łļź╝ ļæÉĻ│Ā ņ׳ļŗż. ņ£ĀņŚŁņØś ņĀĆļźśļ░®ņĀĢņŗØņØĆ Eq. (1)Ļ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ sļŖö ņ£ĀņŚŁņØś ņĀĆļźśļ¤ē, qļŖö ņ£ĀņŚŁņØś ņ£ĀņČ£ļ¤ēņØ┤ļ®░, kņÖĆ pļŖö ņ£ĀņŚŁņØś ļ¼╝ļ”¼ņĀü ĒŖ╣ņä▒ņØä ļéśĒāĆļé┤ļŖö ņĀĆļźś ņāüņłśņØ┤ļŗż. Kimura (1961)ļŖö ņĀĆļźśĒĢ©ņłśļ¬©ĒśĢņŚÉ ņłśņĀĢ puls ļ░®ļ▓ĢņØä Ēś╝ĒĢ®ĒĢśņŚ¼ ņ£ĀņČ£Ļ│Āļź╝ Ļ│äņé░ĒĢśņśĆļŗż.
ņŚ¼ĻĖ░ņä£, r(t)ļŖö ņŗ£Ļ░ä tņŚÉ ļīĆĒĢ£ ņ£ĀņŚŁņŚÉ ļé┤ļ”░ ļŗ©ņ£äņ£Āņ×ģļ¤ē(mm/h), reļŖö ņ┤łĻ│╝ņÜ░ļ¤ē(mm/h), q(t)ļŖö ļŗ©ņ£äņ£ĀņČ£Ļ│Ā, f1ņØĆ ņØ╝ņ░©ņ£ĀņČ£ļźĀ, TlņØĆ ņ¦Ćņ▓┤ņŗ£Ļ░ä(hr), RsaļŖö ĒżĒÖöņÜ░ļ¤ē(mm/h)ņØ┤ļŗż. ĒĢśļÅäņØś ņĀĆļźśļ░®ņĀĢņŗØņØĆ Eq. (2)ņÖĆ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ IļŖö ņ£Āņ×ģļ¤ē, OļŖö ņ£ĀņČ£ļ¤ē, ╬ötļŖö ņŗ£Ļ░ä ļ│ĆĒÖöļ¤ē, ╬öSļŖö ņĀĆļźśņØś ļ│ĆĒÖöļ¤ēņØ┤ļŗż. ņ”ē, ņŗ£Ļ░äļ│ĆĒÖöļ¤ēņŚÉ ļö░ļźĖ ņĀĆļźśļ│ĆĒÖöļ¤ēņØĆ ņ£Āņ×ģļ¤ēĻ│╝ ņ£ĀņČ£ļ¤ēņØś ņ░©ņØ┤ņÖĆ Ļ░ÖņØīņØä ņØśļ»ĖĒĢ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö KŌĆÉwaterņŚÉņä£ Ļ░£ļ░£ĒĢ£ ņĀĆļźśĒĢ©ņłśļ▓Ģ ĻĖ░ļ░śņØś COSFIM ļ¬©ļŹĖļĪ£ ņ£ĀņČ£ņ×ÉļŻīļź╝ ļ¬©ņØśĒĢśņśĆļŗż.
ĒÖŹņłśļ¤ē ņé░ņĀĢ ļ░Å ĒÖŹņłśĒĢ┤ņäØņŚÉ ņ׳ņ¢┤ņä£ Ļ░ĢņÜ░ņØś Ļ│ĄĻ░äļČäĒżļź╝ Ļ│ĀļĀżĒĢ£ ņ£Āļ¤ēņé░ņČ£ņØĆ ĒĢäņłśņĀüņØ┤ļŗż(Kim and Shin, 2017). ņĀäņ▓┤ Ļ░ĢņÜ░ļ¤ēņØ┤ Ļ░ÖņØĆ Ļ▓ĮņÜ░ Ļ░ĢņÜ░ņØś Ļ│ĄĻ░äļČäĒżļź╝ Ļ│ĀļĀżĒĢ┤ņä£ ĒĢ┤ņäØĒĢ£ Ļ▓āĻ│╝ Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖņØĆ Ļ▓āņØś ņ£ĀņČ£ ņłśļ¼ĖĻ│ĪņäĀ ļ░Å ņ▓©ļæÉņ£Āļ¤ēņØś Ēü¼ĻĖ░ļŖö ļŗżļź┤Ļ▓ī ļéśĒāĆļéĀ ņłś ņ׳ĻĖ░ ļĢīļ¼ĖņØ┤ļŗż(Singh, 1997). ĻĘĖļ¤¼ļ»ĆļĪ£ Ļ░ĢņÜ░ņØś Ļ│ĄĻ░äļČäĒżļŖö ĒÖŹņłśļ¤ē ņé░ņĀĢ ļ░Å ĒÖŹņłśĒĢ┤ņäØņŚÉ Ēü░ ņśüĒ¢źņØä ņŻ╝ļ®░ ņØ┤ļŖö Ļ│¦ ņłśņ×ÉņøÉ ņäżĻ│äņŚÉ ņ¦üņĀæņĀüņØĖ ņśüĒ¢źņØä ļ»Ėņ╣śĻĖ░ ļĢīļ¼ĖņŚÉ Ļ░ĢņÜ░ņØś Ļ│ĄĻ░äļČäĒżĻ░Ć ņ£ĀņČ£ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņŚÉ ļīĆĒĢ£ ņĀĢļ¤ēņĀüņØĖ ļČäņäØņØ┤ ņÜöĻĄ¼ļÉ£ļŗż. ļö░ļØ╝ņä£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ│ĄĻ░äļČäĒżļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśĻĖ░ ņ£äĒĢ┤ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØĆ Ļ│äņĖĪņ£ĀņŚŁņØś Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīļĪ£ ņČöņĀĢĒĢ£ ļ¦żĻ░£ļ│Ćņłśļź╝ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņŚÉ ņĀüņÜ®ĒĢśņŚ¼ ņĀĆļźśĒĢ©ņłśļ¬©ĒśĢ ĻĖ░ļ░śņØś ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīļź╝ ņāØņé░ĒĢśļŖö ļ░®ļ▓ĢņØ┤ļŗż. ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØś Ļ░£ļģÉņØĆ ļŗżļźĖ ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉ£ ņĀüņØ┤ ņ׳ļŗż. ņØ┤ņĀäņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¢┤ļŖÉ ĒĢ£ ņ£ĀņŚŁņØś ņ£ĀņČ£ ņČ£ĻĄ¼ ņ¦ĆņĀÉņØä ĻĖ░ņżĆņ£╝ļĪ£ ņ£ĀņŚŁņŚÉ ļīĆĒĢ£ ņĄ£ņĀüņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöņĀĢĒĢśņŚ¼ ļ¬©ņØśĒĢ£ ņ£ĀņČ£ņØä Ļ┤ĆņĖĪņ£ĀņČ£ņŚÉ ņĄ£ļīĆĒĢ£ ņ£Āņé¼ĒĢśĻ▓ī ļ¦īļō£ļŖö ļ░®ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż(Bae and Chung, 2000; Kim et al., 2008, Chung et al., 2012). ļŗżļźĖ ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¢┤ļŖÉ ĒĢ£ ņ£ĀņŚŁņØä ņżæņåīĻĘ£ļ¬© ļŗ©ņ£äļĪ£ ļéśļłäĻ│Ā Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ü ņåīņ£ĀņŚŁņŚÉ ļīĆĒĢ£ ņĄ£ņĀüņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöņĀĢĒĢ£ ļÆż, ņØ┤ ļ¦żĻ░£ļ│ĆņłśļĪ£ Ļ░ü ņåīņ£ĀņŚŁņØś ņ£ĀņČ£ļ¤ēņØä ņé░ņĀĢĒĢśļŖö ļ░®ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż(Kim et al., 2013). ņĄ£ĻĘ╝ņŚÉļŖö ņ¦ĆņŚŁĒÜīĻĘĆļ¬©ĒśĢņØś ņäżļ¬ģļ│ĆņłśņŚÉ ņłśļ¼Ėļ¬©ĒśĢņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöĻ░ĆĒĢśņŚ¼ ĒÜīĻĘĆļ¬©ĒśĢņØś ņĀüĒĢ®ņä▒ņØä Ē¢źņāüĒĢ£ ĒĢśņØ┤ļĖīļ”¼ļō£ ņ¦ĆņŚŁĒÖö ļ¬©ĒśĢņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśĻĖ░ļÅä ĒĢśņśĆļŗż(Kim et al., 2018). ņØ┤ņ▓śļ¤╝ Ļ│ĄĻ░äņ×ÉļŻīĒÖĢņןļ░®ļ▓ĢņØĆ Ļ│äņĖĪ Ļ░ĆļŖźĒĢ£ ņ£ĀņŚŁņØś Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīļź╝ ņé¼ņÜ®ĒĢśņŚ¼ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£Āļ¤ē ņ×ÉļŻīļź╝ ņāØņä▒ĒĢĀ ņłś ņ׳ņ£╝ļ®░, ļČäĒĢĀĒĢ£ ņåīņ£ĀņŚŁņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöņĀĢĒĢśņŚ¼ Ļ░ü ņåīņ£ĀņŚŁņØś ņ£ĀņČ£ļ¤ēņØä ņé░ņĀĢĒĢśļ»ĆļĪ£ ĒĢśļéśņØś ņ£ĀņŚŁņØś ņ£ĀņČ£ņØä ņŚ¼ļ¤¼ Ļ░£ņØś ņ£ĀņČ£ļĪ£ ļéśļłäļŖö ĒÜ©Ļ│╝Ļ░Ć ņ׳ļŗż.
Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīņÖĆ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņØś ņ░©ņØ┤ļź╝ ļ╣äĻĄÉĒĢśņŚ¼ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØś ļ¦żĻ░£ļ│Ćņłśļź╝ ņĄ£ņĀüĒÖöĒĢśĻĖ░ ņ£äĒĢ┤ NashŌĆÉSutcliffe Efficiency (NSE; Nash and Sutcliffe, 1970)ļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. NSEļŖö ļ¬©ņØśĻ░ÆņØä Ļ┤ĆņĖĪĻ░ÆĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ ĒāĆļŗ╣ĒĢ£ ļ¦żĻ░£ļ│Ćņłśļź╝ ņČöņĀĢĒĢśļŖö ļ¬®ņĀüĒĢ©ņłśņØ┤ļŗż. ļ¬©ņØśĻ░ÆņØś ņĀĢĒÖĢļÅäļź╝ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ņäżļ¬ģĒĢĀ ņłś ņ׳ņ£╝ļ®░, ņłśļ¼Ė ļČäņĢ╝ņŚÉņä£ ļ¦żĻ░£ļ│Ćņłś ļ│┤ņĀĢ ļ░Å ņĀüņĀłņä▒ Ļ▓ĆņĀĢņØä ĒĢĀ ņłś ņ׳ņ¢┤ ļ¬®ņĀüĒĢ©ņłśļĪ£ ļäÉļ”¼ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņé¼ņÜ®ĒĢ£ ļ¦żĻ░£ļ│ĆņłśļŖö ļ¼╝ļ”¼ņĀü ļ¦żĻ░£ļ│Ćņłś(k, p, Tl)ņÖĆ ņé¼ņāüņżæņŗ¼ ļ¦żĻ░£ļ│Ćņłś(f1, Rsa)ļĪ£ ĻĄ¼ļČäĒĢśņ¦Ćļ¦ī ļ¬©ļōĀ Ļ│ĄĻ░äņĀü ļ¦żĻ░£ļ│Ćņłśļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ņ£ĀņČ£ņØä ļ¬©ņØśĒĢśĻĖ░ņŚÉļŖö ĒśäņŗżņĀüņ£╝ļĪ£ ņ¢┤ļĀżņÜ┤ ļČĆļČäņØ┤ ņ׳ņ£╝ļ»ĆļĪ£ ļ¼╝ļ”¼ņĀü ļ¦żĻ░£ļ│Ćņłś(k, p, Tl)ņÖĆ f1(ņ£ĀņČ£ļźĀ)ņØä Ļ│ĀņĀĢĒĢśņśĆļŗż. ĻĘĖļ”¼Ļ│Ā ļ¬®ņĀüĒĢ©ņłś NSEļź╝ ĻĖ░ņżĆņ£╝ļĪ£ Rsa(ĒżĒÖöņÜ░ļ¤ē)ļź╝ ņŗ£Ē¢ēņ░®ņśżļ▓Ģņ£╝ļĪ£ ļ│┤ņĀĢĒĢśņŚ¼ ņĄ£ņĀüĒÖöĒĢśļŖö ņĀłņ░©ļź╝ ļ░¤ņĢśļŗż.
ņŚ¼ĻĖ░ņä£ Q o Q m t Q o t
ņé░ņĀĢĒĢ£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņŚÉ Ļ░Ćņן ņĀüĒĢ®ĒĢ£ ĒÖŹņłśļ¤ē ņé░ņĀĢ ļ░®ļ▓ĢņØä ņ░ŠĻĖ░ ņ£äĒĢ┤ Pearson correlation coefficient (PearsonŌĆÖs r)Ļ│╝ Root Mean Square Error(RMSE, ĒÅēĻĘĀņĀ£Ļ│▒ĻĘ╝ ņśżņ░©) Ļ▓Ćņ”Øļ░®ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż. PearsonŌĆÖs rĻ│╝ RMSEļŖö ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ X, YļŖö Ļ░ü ļ│ĆņłśņØś ļ│Ćļ¤ē, nņØĆ ļ│Ćļ¤ēņØś Ļ░£ņłśļŗż. rņØĆ - 1 Ōēż r Ōēż 1ņØś ļ▓öņ£äļź╝ Ļ░Ćņ¦äļŗż. +1ņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ ņ¢æņØś ņāüĻ┤ĆĻ┤ĆĻ│ä, ŌĆÉ1ņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ ņØīņØś ņāüĻ┤ĆĻ┤ĆĻ│ä, 0ņØĆ ņāüĻ┤ĆĻ┤ĆĻ│äĻ░Ć ņĪ┤ņ×¼ĒĢśņ¦Ć ņĢŖļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż.
ņŚ¼ĻĖ░ņä£ NņØĆ ņ×ÉļŻīņØś Ļ░£ņłś, MiļŖö ņśłņĖĪĻ░Æ, OiļŖö Ļ┤ĆņĖĪĻ░ÆņØä ņØśļ»ĖĒĢ£ļŗż. RMSEņØś Ļ▓Ćņ”ØĻ░ÆņØĆ 0ņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ Ļ┤ĆņĖĪĻ░ÆĻ│╝ ņśłņĖĪĻ░ÆņØ┤ ņä£ļĪ£ ņ£Āņé¼ĒĢ£ Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż. RMSEļŖö ļæÉ Ēæ£ļ│ĖņØś ņØĖĻ│╝Ļ┤ĆĻ│äļź╝ Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖĻ│Ā ļ¬©ņØśĻ░ÆĻ│╝ Ļ┤ĆņĖĪĻ░Æ ņé¼ņØ┤ņØś(ļśÉļŖö Ēæ£ļ│Ė ņé¼ņØ┤) ņ░©ņØ┤ļ¦īņØä ļ╣äĻĄÉĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņ£ĀĒśĢņØ┤ ļŗżļźĖ ņ×ÉļŻīņØś ļ╣äĻĄÉļŖö ņ£ĀĒÜ©ĒĢśņ¦Ć ņĢŖļŗż(Hyndman et al., 2006). ļö░ļØ╝ņä£ RMSEļĪ£ Ļ▓Ćņ”ØĒĢśĻĖ░ ņĀäņŚÉ PearsonŌĆÖs rņØä ņé¼ņÜ®ĒĢśņŚ¼ ļæÉ Ēæ£ļ│Ė ņé¼ņØ┤ņŚÉ ņāüĻ┤Ćņä▒ņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓Ģņ£╝ļĪ£ ņé░ņĀĢĒĢ£ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņÖĆ ĒÖŹņłśļ¤ē ņé░ņĀĢ ļ░®ļ▓Ģ ņé¼ņØ┤ņŚÉ ņāüĻ┤Ćņä▒ņØä ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ PearsonŌĆÖs rļĪ£ Ļ▓Ćņ”ØĒĢśņśĆņ£╝ļ®░, ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņŚÉ Ļ░Ćņן ņĀĢĒÖĢļÅäĻ░Ć ļåÆņØĆ ĒÖŹņłśļ¤ē ņé░ņĀĢ ļ░®ļ▓ĢņØä ņ░ŠĻĖ░ ņ£äĒĢ┤ RMSEļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż.
ĒÖŹņłśņ¦ĆĒśĢĒĢÖņ×É Horton (1932, 1945)Ļ│╝ Strahler (1952, 1964)ņØĆ ņ£ĀņČ£Ļ│╝ ņ¦üņĀæņĀüņ£╝ļĪ£ Ļ┤ĆļĀ©ņØ┤ ņ׳ļŖö ļ¼╝ļ”¼ņĀü ĒŖ╣ņä▒ņØä ņĪ░ņé¼ĒĢ£ Ļ▓░Ļ│╝ ĒĢśņ▓£ĻĖĖņØ┤, ĒĢśņ▓£ņł£ņä£, ņ£ĀņŚŁļ®┤ņĀü, ņ£ĀņŚŁĻ▓Įņé¼, ņ▒äļäÉĻ▓Įņé¼, ņĪ░ļÅäĻ│äņłś ļō▒ņØś ļ¦żĻ░£ļ│ĆņłśĻ░Ć ņ£ĀņČ£ņŚÉ ņżæļīĆĒĢ£ ņśüĒ¢źņØä ļ»Ėņ╣śļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż. Kovacs (1988)ļŖö ņØ┤ Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ ņ▓©ļæÉņ£Āļ¤ēņØ┤ ņ£ĀņŚŁļ®┤ņĀü ļ░Å ņ£ĀņŚŁ ĒŖ╣ņä▒ņŚÉ ļīĆĒĢ┤ ņāüĻ┤Ćņä▒ņØä ļéśĒāĆļéĖ QRMFņŗØņØä ņĀ£ņĢłĒĢśņśĆļŗż. QRMFņŗØņØĆ ņłśļ¼ĖĒĢÖņĀüņ£╝ļĪ£ ļÅÖņ¦łĒĢ£ ņ£ĀņŚŁņŚÉ ļīĆĒĢ┤ ņĄ£ļīĆ ņ▓©ļæÉņ£Āļ¤ēņØä ņČöņĀĢĒĢśņŚ¼ ņŻ╝ņ¢┤ņ¦ä ņ¦ĆņŚŁņØś ņśłņāü ņ▓©ļæÉņ£Āļ¤ēņØä ņĀĢņØśĒĢśļŖö Ļ│ĪņäĀņØä ņé░ņČ£ĒĢśļŖö ņŗØņØ┤ļŗż(Pegram and Parak, 2004).
ņŚ¼ĻĖ░ņä£ QRMFļŖö ņ¦ĆņŚŁņĄ£ļīĆĒÖŹņłśļ¤ē(m3/s), AļŖö ņ£ĀņŚŁļ®┤ņĀü(km2), KļŖö ņ£ĀņŚŁņØś ņ¦Ćņ¦łĒĢÖņĀü ĒŖ╣ņ¦Ģ, ņ¦ĆĒśĢĒśĢĒā£, ņŗØņāØņØś ļČäĒż, ņ£ĀņŚŁ Ļ▓Įņé¼ ļō▒ ņ£ĀņŚŁņØś ĒŖ╣ņä▒ņØä ļéśĒāĆļé┤ļŖö ļ¼┤ņ░©ņøÉ Ļ│äņłśļŗż. KĻ░ÆņØĆ ņ£ĀņŚŁļ¦łļŗż ļŗżļź┤ļ®░ Ļ░ÖņØĆ ņ£ĀņŚŁņØ┤ņ¢┤ļÅä ņ£ĀņŚŁņØä ļČäĒĢĀĒĢśĻ▒░ļéś ņŗ£Ļ░äņØ┤ ņ¦Ćļé©ņŚÉ ļö░ļØ╝ ņ£ĀņŚŁ ĒŖ╣ņä▒ņØ┤ ļ│ĆĒÖöĒĢśļ®┤ KĻ░ÆļÅä ļ│ĆĒĢĀ ņłś ņ׳ļŗż. ļśÉĒĢ£, Ļ▒┤ņäżĻĄÉĒåĄļČĆņŚÉņä£ ņĀ£ņŗ£ĒĢ£ ļ╣äņ£Āļ¤ēļ▓ĢņØä ņČöĻ░ĆĒĢśņŚ¼ ļ╣äĻĄÉĒĢśņśĆļŗż. ļ╣äņ£Āļ¤ēļ▓ĢņØĆ ņ£Āļ¤ēņØä ņ¦üņĀæ ņĖĪņĀĢĒĢĀ ņłś ņŚåļŖö ņ£ĀņŚŁņØä ņäĀņĀĢĒĢśņŚ¼ ļŗ©ņ£äļ®┤ņĀüņŚÉ ļīĆĒĢ£ ĒÅēĻĘĀņ£ĀņČ£Ļ│Āļź╝ ņé░ņĀĢĒĢśņŚ¼ ņ£Āļ¤ēņØä ņČöņĀĢĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ▓©ļæÉĒÖŹņłśļ¤ēņØä ņé░ņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņé¼ņÜ®ĒĢ£ļŗż. ļ╣äņ£Āļ¤ēļ▓Ģ Ļ│ĄņŗØņØĆ ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ qļŖö ļŗ©ņ£äļ®┤ņĀüļŗ╣ ņŚ░ĒÅēĻĘĀņĄ£ļīĆĒÖŹņłśļ¤ē(m3/sec/km2), AļŖö ņ£ĀņŚŁļ®┤ņĀü(km2)ņØ┤ļŗż. Fig. 2ņŚÉ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśĻĖ░ ņ£äĒĢ£ ņĀäļ░śņĀüņØĖ Ļ│╝ņĀĢņØä ļéśĒāĆļāłļŗż. ĒÖŹņłśļ¤ēņØś ņČöņĀĢņŚÉ ņ׳ņ¢┤ņä£, ĒÅēĻĘĀņ£ĀņČ£ņ×ÉļŻīĻ░Ć ņĄ£ļīĆņ£ĀņČ£ņ×ÉļŻīņŚÉ ļ╣äĒĢ┤ ļé«Ļ▓ī ļéśĒāĆļéśĻĖ░ ļĢīļ¼ĖņŚÉ Ļ░ü ņé¼ņāüņØä ĒÅēĻĘĀņØä ļé┤ņ¢┤ ĒĢśļéśņØś ņé¼ņāüņ£╝ļĪ£ ļéśĒāĆļé┤ļ®┤ ĒÖŹņłśļ¤ēņØä ņČöņĀĢĒĢśļŖö ļ¬®ņĀüņŚÉ ņĀüņĀłĒĢśņ¦Ć ņĢŖņØä ņłś ņ׳ļŗż. ļö░ļØ╝ņä£ ĒÅēĻĘĀņ£ĀņČ£ņ×ÉļŻīĻ░Ć ņĢäļŗī ņĄ£ļīĆņ£ĀņČ£ņ×ÉļŻīņØä ņé¼ņÜ®ĒĢśņŚ¼ ĒÖŹņłśņé¼ņāüņØä ĒÅēĻ░ĆĒĢśņśĆņ£╝ļ®░, ņ£ĀņČ£ļ¤ēņØ┤ Ļ░Ćņן ļ¦ÄņØĆ ņŚ░ļÅäļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒ¢łļŗż. ļśÉĒĢ£, ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓Ģņ£╝ļĪ£ ņāØņä▒ĒĢ£ ļ¬©ņØś ņ£Āļ¤ēņØä ļ╣äĒÖŹņłśļ¤ēņ£╝ļĪ£ ļ│ĆĒÖśĒĢśņŚ¼ QRMF ļ░Å ļ╣äņ£Āļ¤ēļ▓ĢĻ│╝ ļ╣äĻĄÉĒĢśņśĆņ£╝ļ®░, ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś KĻ░ÆņØä Ļ│äņé░ĒĢśļŖö ņĀłņ░©ļź╝ ļ░¤ņĢä ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒĢĀ ņłś ņ׳ļŖöņ¦Ć ĒÖĢņØĖĒĢśņśĆļŗż.
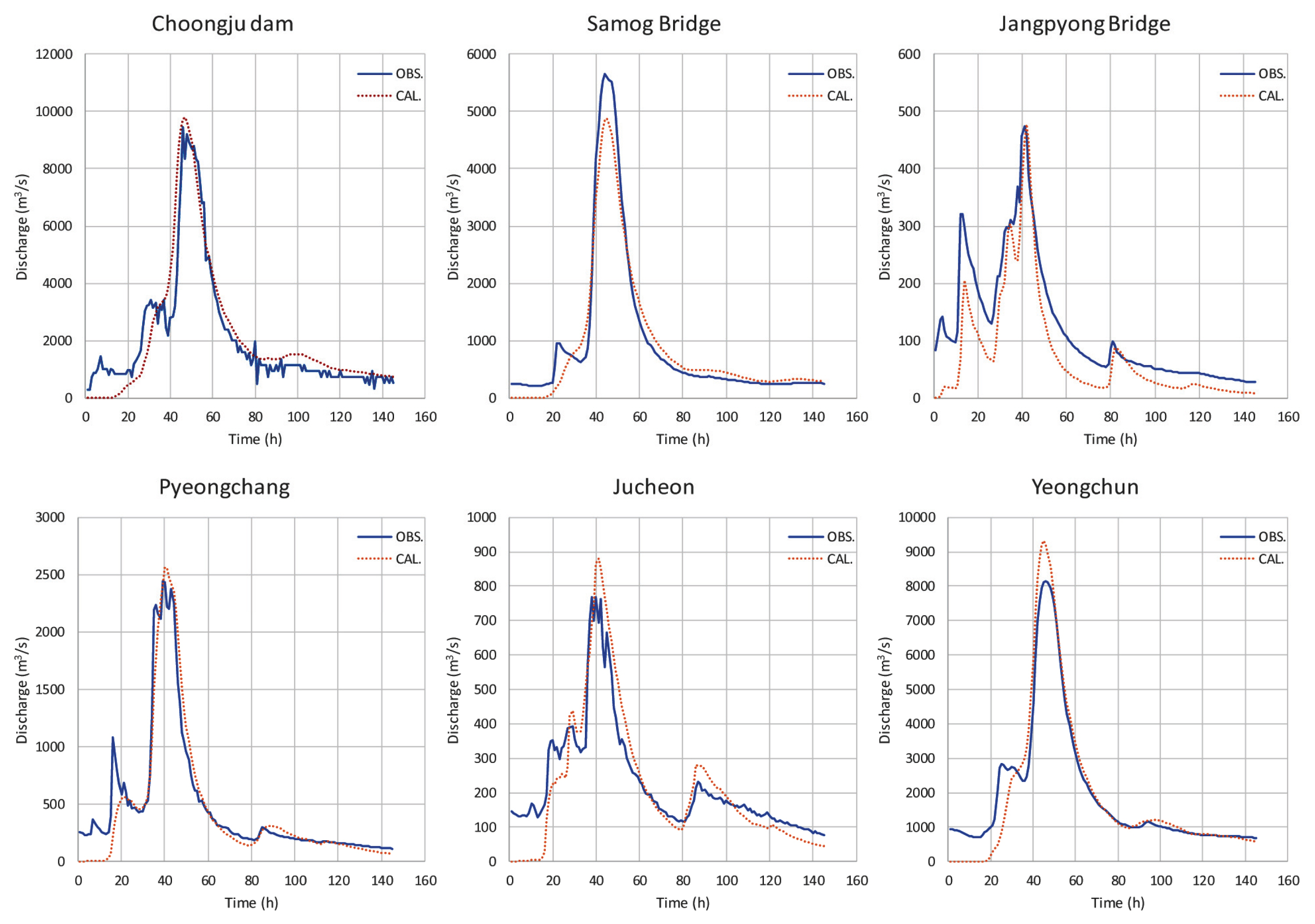
Ļ░ü ņ£ĀņŚŁņŚÉņä£ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ņāØņä▒ļÉ£ ļ¬©ņØś ņ£Āļ¤ēņ£╝ļĪ£ ņ£ĀņŚŁĻ│╝ ņ▒äļäÉ ņé¼ņØ┤ņØś ĒÖŹņłśņČöņĀüļ░®ļ▓Ģ(Flood Routing)ņØä ĒåĄĒĢ┤ ņĄ£ļīĆ 75Ļ░£ ņ£ĀņŚŁņŚÉ ļīĆĒĢ£ ņ£ĀņČ£ļ¤ēņØä ņé░ņČ£ĒĢśņśĆļŗż. ņĄ£ņĀüĒÖöĒĢ£ RsaņÖĆ ņČ®ņŻ╝ļīÉ ĻĖ░ņżĆ(ņ£ĀņŚŁņČ£ĻĄ¼ņ¦ĆņĀÉ)ņØś NSE Ļ░ÆņØä Table 1ņŚÉ ļéśĒāĆļāłļŗż. Fig. 3ņØĆ 2008ļģäņØś ņČ®ņŻ╝ļīÉ, ņé╝ņśźĻĄÉ, ņןĒÅēĻĄÉ, ĒÅēņ░Į, ņŻ╝ņ▓£, ņśüņČś ņłśņ£äĻ┤ĆņĖĪņåīļź╝ ļīĆĒæ£ļĪ£ ĒĢśņŚ¼ Ļ┤ĆņĖĪņ£Āļ¤ēņ×ÉļŻīņÖĆ ļ¬©ņØśņ£Āļ¤ēņ×ÉļŻīļź╝ ļéśĒāĆļéĖ ĻĘĖļלĒöäņØ┤ļŗż. ņé╝ņśźĻĄÉ ļ░Å ņןĒÅēĻĄÉ ņłśņ£äĻ┤ĆņĖĪņåīņŚÉņä£ļŖö ņŗżņĀ£Ļ┤ĆņĖĪņ£Āļ¤ēņ×ÉļŻīņŚÉ ļ╣äĒĢ┤ Ļ│╝ņåīĒÅēĻ░ĆĒĢśņŚ¼ ļ¬©ņØśļÉ£ Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ĒŖ╣Ē׳ ņןĒÅēĻĄÉļŖö ņĀäņ▓┤ņĀüņ£╝ļĪ£ ļ¬©ņØśņ×ÉļŻīĻ░Ć Ļ┤ĆņĖĪņ×ÉļŻīļ│┤ļŗż ņĀüĻ▓ī ĒÅēĻ░ĆļÉśņŚłļŗż. ņśüņČśņØĆ ņ▓©ļæÉļČĆļČäņŚÉ Ļ┤ĆņĖĪņ×ÉļŻīļ│┤ļŗż ļ¦ÄĻ▓ī ļ¬©ņØśļÉśņŚłņ£╝ļ®░, Ļ░Ćņן ĒĢśļźśņŚÉ ņ£äņ╣śĒĢ£ ņČ®ņŻ╝ļīÉ ņłśņ£äĻ┤ĆņĖĪņåīļŖö Ļ┤ĆņĖĪņ£Āļ¤ēņŚÉ Ļ░ĆĻ╣ØĻ▓ī ņĀüņĀłĒ׳ ļ¬©ņØśļÉ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņØ┤Ļ▓āņØĆ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ ļ¬©ņØśņ£Āļ¤ēņØś ņČöņĀĢņØĆ ņĀüņĀłĒĢśļŗżļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī ņłśņ£äĻ┤ĆņĖĪņåī ļīĆļČĆļČäņŚÉņä£ ņ┤łĻĖ░ĻĖ░Ļ░äņØś ļ¬©ņØś ņ£Āļ¤ēņØä ļīĆņ▓┤ļĪ£ ļ¬©ņØśĒĢśņ¦Ć ļ¬╗ĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņØ┤ļŖö ĻĖ░ņĀĆņ£Āļ¤ēņØä Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖĻ│Ā ļ¬©ņØśĒ¢łĻĖ░ ļĢīļ¼ĖņŚÉ ņ┤łĻĖ░ņŗ£Ļ░äņŚÉ ļīĆĒĢ┤ Ļ│╝ņåīĒÅēĻ░ĆĒĢ£ Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż. ļö░ļØ╝ņä£ ņäĀĒ¢ē Ļ░ĢņÜ░ņŚÉ ļö░ļźĖ ĻĖ░ņĀĆņ£Āļ¤ē ņ×ÉļŻīļź╝ ņĀüņÜ®ĒĢ£ļŗżļ®┤ ĻĖ░ņĪ┤ņØś ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīļ│┤ļŗż ņĀüņĀłĒĢ£ Ļ▓░Ļ│╝Ļ░Ć ļéśņś¼ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ĒĢśņśĆļŗż.
Fig. 4ļŖö ņČ®ņŻ╝ļīÉ, ņśüņøö, ņśüņČśņŚÉņä£ ļ¬©ļōĀ ļČäņäØ ĻĖ░Ļ░äņØś Ļ┤ĆņĖĪ ņ£Āļ¤ēĻ│╝ ļ¬©ņØś ņ£Āļ¤ēņØś ļ╣äĻĄÉļź╝ ļéśĒāĆļéĖ ĻĘĖļלĒöäņØ┤ļŗż. NSEĻ░ÆņØĆ ņČ®ņŻ╝ļīÉ, ņśüņøö, ņśüņČśņŚÉņä£ Ļ░üĻ░ü 0.53, ŌĆÉ0.46, 0.48ņØä ļéśĒāĆļé┤ņ¢┤ ņśüņøöĻ│╝ ņśüņČśņŚÉņä£ 0.5ļ│┤ļŗż ņ×æņØĆ Ļ░ÆņØ┤ ļéśĒāĆļéś ņĀüņĀłĒĢśņ¦Ć ņĢŖņĢśņ¦Ćļ¦ī, ņśüņČśņØĆ ņØ┤ņāüņĀÉ(outlier)ņØś ņśüĒ¢źņ£╝ļĪ£ ļ│┤Ļ│Ā ņĀüņĀłĒĢśļŗżĻ│Ā ĒīÉļŗ©ĒĢśņśĆļŗż. ņāüņ£ä ņ£ĀņŚŁņŚÉņä£ ĻĖ░ņżĆņŚÉ ļ¬╗ ļ»Ėņ╣śĻ▓ī ļ¬©ņØśĻ░Ć ļÉśņŚłņ¦Ćļ¦ī ņ£Āļ¤ēņØĆ ņ£ĀņŚŁ ņČ£ĻĄ¼ ņ¦ĆņĀÉņ£╝ļĪ£ ņ¦æņżæļÉ£ļŗżļŖö ņĀÉņØä ņ░Ėņ×æĒĢśņŚ¼ Ļ░Ćņן ĒĢśļźśņŚÉ ņ£äņ╣śĒĢśļŖö ņ£ĀņŚŁ ņČ£ĻĄ¼ ņ¦ĆņĀÉņØĖ ņČ®ņŻ╝ļīÉņŚÉņä£ 0.53ņ£╝ļĪ£ ļ¦īņĪ▒ĒĢśņśĆņ£╝ļ»ĆļĪ£ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢ£ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻī ņé░ņĀĢņØĆ ņĀüņĀłĒĢśļŗżĻ│Ā ĒīÉļŗ©ĒĢśņśĆļŗż. ļśÉĒĢ£, ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņØś ņ▓©ļæÉļ░£ņāØņŗ£Ļ░äņØ┤ ņŗżņĀ£ ņ£ĀņŚŁņØś ĒŖ╣ņä▒Ļ│╝ ņ£Āņé¼ĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. Fig. 5ļŖö ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņØś ņ£ĀĒÜ©ņÜ░ļ¤ē ņŗ£ņ×æļČĆĒä░ ņ▓©ļæÉņ£Āļ¤ē ļ░£ņāØĻ╣īņ¦ĆņØś ņŗ£Ļ░äņØä ļéśĒāĆļéĖ ĻĘĖļלĒöäņØ┤ļ®░, ņ£ĀņŚŁļ®┤ņĀüņØ┤ ņ╗żņ¦łņłśļĪØ ņ▓©ļæÉļ░£ņāØņŗ£Ļ░äņØ┤ ņ¦ĆņŚ░ļÉśļŖö ņŗżņĀ£ ņ£ĀņČ£ņ×ÉļŻīņÖĆ ņ£Āņé¼ĒĢ£ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņØś ĒŖ╣ņä▒ņØä ļ│╝ ņłś ņ׳ņŚłļŗż.
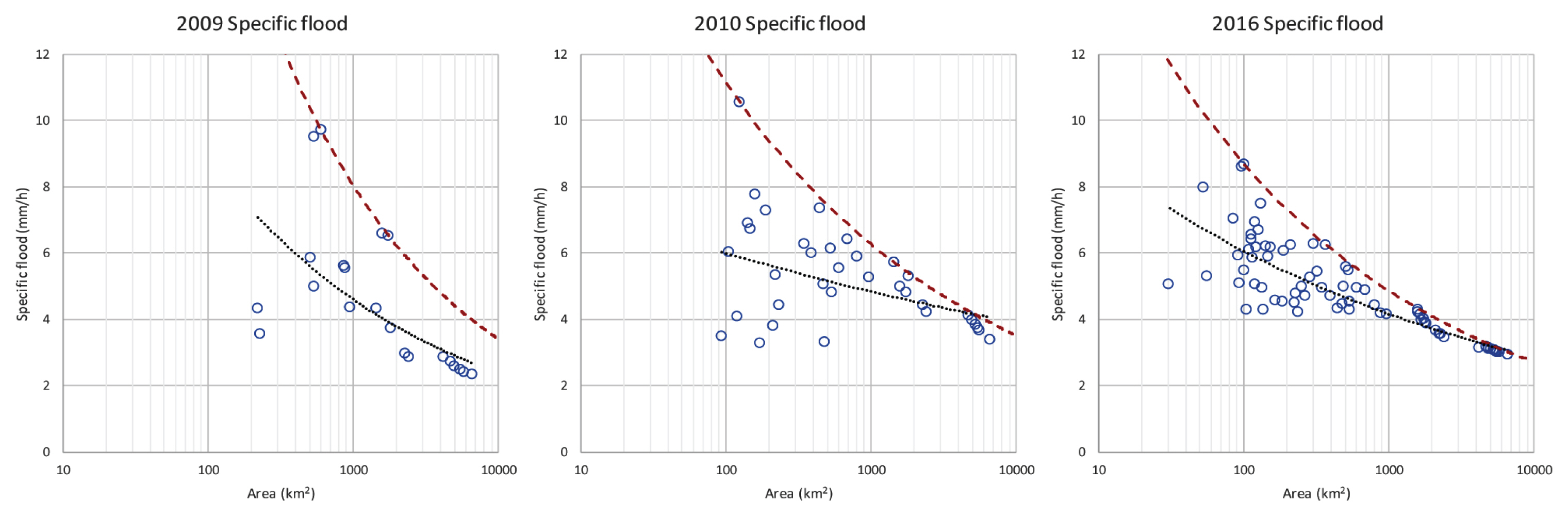
ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņāØņä▒ĒĢ£ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīļź╝ ļ╣äĒÖŹņłśļ¤ēņ£╝ļĪ£ ļ│ĆĒÖśĒĢśņŚ¼ Fig. 6Ļ│╝ Ļ░ÖņØ┤ ļéśĒāĆļāłļŗż. Fig. 6ņØĆ 2009, 2010, 2016ļģäņØś ļ╣äĒÖŹņłśļ¤ēņØä ļéśĒāĆļé┤ļŖö ĻĘĖļלĒöäņØ┤ļŗż. Ļ░ĆļĪ£ņČĢņØĆ ņ£ĀņŚŁļ®┤ņĀü(km2)ņØ┤ļ®░ ņäĖļĪ£ņČĢņØĆ ņ£ĀņČ£ļ¤ē(m3)ņØä ņ£ĀņŚŁļ®┤ņĀü(km2)ņ£╝ļĪ£ ļéśļłł ļ╣äĒÖŹņłśļ¤ē(mm/h)ņØ┤ļŗż. ņĀÉņØĆ Ļ░ü ņ£ĀņŚŁņØś ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻī, ņĀÉņäĀņØĆ ļ¬©ņØśļ╣äĒÖŹņłśļ¤ēņØś Ļ▓ĮĒ¢źņä▒, Ļ░ĆļŖö ņŗżņäĀņØĆ ļ¬©ņØśļ╣ä ĒÖŹņłśļ¤ēņØś ņĄ£ļīĆņ╣ś Ļ▓ĮĒ¢źņä▒ņØä ļéśĒāĆļéĖļŗż. ņłśņ×ÉņøÉņäżĻ│äņŗ£ ņ▓©ļæÉĒÖŹņłśļ¤ēņØä ĻĖ░ņżĆņ£╝ļĪ£ ņäżĻ│äĒĢśļ»ĆļĪ£ ĒÖŹņłśļ¤ēņØś ņĄ£ņåīņ╣śļŖö Ēæ£ņŗ£ĒĢśņ¦Ć ņĢŖņĢśļŗż. Fig. 6ņØä ļ│┤ļ®┤ ņ£ĀņŚŁņØ┤ ĒĢśļźśņŚÉ ņ£äņ╣śĒĢĀņłśļĪØ(ņ£ĀņŚŁļ®┤ņĀüņØ┤ ņ╗żņ¦łņłśļĪØ) ļ╣äĒÖŹņłśļ¤ēņØ┤ ņ×æņĢäņ¦ĆĻ│Ā ļČäĒżĻ░Ć ņóüņĢäņ¦ĆļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłņ£╝ļ®░, ņ£ĀņŚŁļ®┤ņĀüĻ│╝ ļ╣äĒÖŹņłśļ¤ēņØś power law Ļ┤ĆĻ│äļź╝ ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż. ņØ┤ ĒŖ╣ņ¦ĢņØĆ Ļ░ĢņÜ░ļČäĒżĻ░Ć ņ£ĀņŚŁ ņĀäņ▓┤ņŚÉ Ļ▒Ėņ│É ļČłĻĘĀņ¦łĒĢśĻ│Ā Ļ░ĢņÜ░ Ļ░ĢļÅäĻ░Ć ņØ╝ņĀĢĒĢśņ¦Ć ņĢŖņØä ļĢī ņ£ĀņŚŁļ│äļĪ£ ņ£ĀņČ£ļ¤ēņØś ņ░©ņØ┤Ļ░Ć ļéśĒāĆļéśĻ▓ī ļÉśņ¢┤ ļ╣äĒÖŹņłśļ¤ēņØś ļČäĒżĻ░Ć ņóüņĢäņ¦ĆļŖö ĒśäņāüņØ┤ļŗż. ņ”ē, ņ×ÉņŚ░ņĀüņØĖ Ļ░ĢņÜ░Ļ░Ć ļé┤ļ”┤ Ļ▓ĮņÜ░ ņØ╝ļ░śņĀüņØĖ ņ£ĀņČ£ļĪ£ ļéśĒāĆļéśļŖö ĒśäņāüņØ┤ļ»ĆļĪ£ ņé░ņĀĢĒĢ£ ņ£ĀņČ£ņ×ÉļŻīļŖö ņŗżņĀ£ ņ£ĀņČ£Ļ│╝ ņ£Āņé¼ĒĢ£ Ļ▓āņ£╝ļĪ£ ļ│┤ņĢśņ£╝ļ®░, ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢśņŚ¼ ņé░ņĀĢĒĢ£ ņ£ĀņČ£ņ×ÉļŻīļŖö ņĀüņĀłĒĢśĻ▓ī ļ¬©ņØśļÉśņŚłļŗżĻ│Ā ĒīÉļŗ©Ē¢łļŗż.
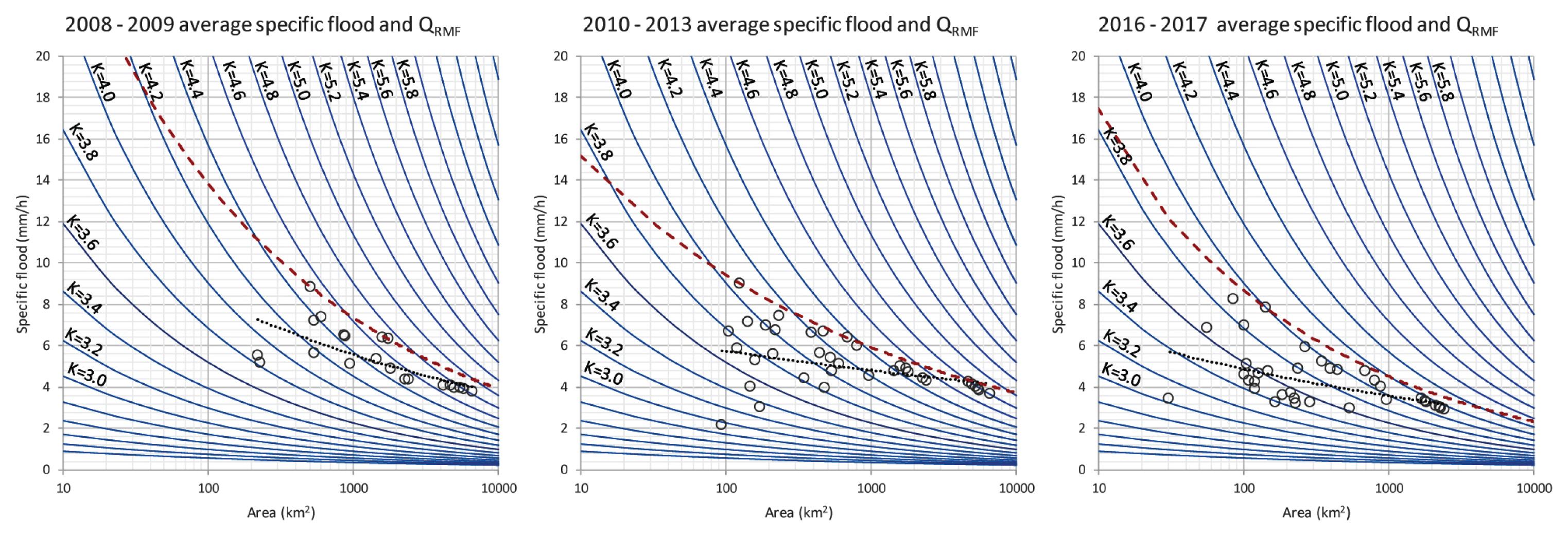
ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņĄ£ĻĘ╝ ņ£ĀņČ£ Ļ▓ĮĒ¢źņä▒ņØä ļČäņäØĒĢśĻĖ░ ņ£äĒĢ┤ 2008~2009ļģä, 2010~2013ļģä, 2016~2017ļģäņØś QRMFņÖĆ ļ¬©ņØśņ£Āļ¤ēņ×ÉļŻīļź╝ ļ╣äĒÖŹņłśļ¤ēņ£╝ļĪ£ ļ│ĆĒÖśĒĢśņŚ¼ Figs. 7 ļ░Å 8ņŚÉ ļéśĒāĆļāłļŗż. ņŗżņäĀņØĆ QRMF KĻ░ÆņØä 2ņØś Ļ░äĻ▓®ņØä ļæÉņ¢┤ ļÅäņŗ£ĒĢ£ QRMFņØś ļ╣äĒÖŹņłśļ¤ēņØ┤ļŗż. ņĄ£ļīĆļ¬©ņØśļ╣äĒÖŹņłśļ¤ēĻ│╝ QRMFņØś ļ╣äĒÖŹņłśļ¤ēņŚÉ ļīĆĒĢ┤ ļ╣äĻĄÉĒĢśĻĖ░ ņ£äĒĢ┤ ņ£ĀņČ£ļ¤ēņØ┤ Ļ░Ćņן ļ¦ÄņØĆ 2010~2013ļģä ĻĖ░Ļ░äņØä ņäĀņĀĢĒĢśņśĆļŗż. Ēö╝ņ¢┤ņŖ© ņāüĻ┤ĆĻ│äņłśņÖĆ RMSEņØś ĒÅēĻ░Ć Ļ▓░Ļ│╝ļź╝ Table 2ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. Ēö╝ņ¢┤ņŖ© ņāüĻ┤ĆĻ│äņłśļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĒÅēĻ░ĆĒĢ£ Ļ▓░Ļ│╝ Pearson's rņØĆ Ļ▒░ņØś 1ņŚÉ ĻĘ╝ņĀæĒĢśņŚ¼ ļ¬©ņØśļ╣äĒÖŹņłśļ¤ēņØś ņĄ£ļīĆņ╣ś ņČöņäĖņäĀĻ│╝ QRMFĻ│ĪņäĀņØĆ ņä£ļĪ£ ņāüĻ┤ĆĻ┤ĆĻ│äĻ░Ć ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ļ╣äņ£Āļ¤ēļ▓Ģ ļśÉĒĢ£ Pearson's rņØ┤ 0.9ņØ┤ņāüņ£╝ļĪ£ ņĄ£ļīĆļ¬©ņØśļ╣äĒÖŹņłśļ¤ēĻ│╝ ņāüĻ┤ĆĻ┤ĆĻ│äĻ░Ć ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ĒŖ╣Ē׳ RMSE ļ╣äĻĄÉļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļČäņäØĒĢ£ Ļ▓░Ļ│╝ QRMF(K=5)ņØś RMSEļŖö 1.941ļĪ£ QRMF(K=5)ņØ╝ ļĢī ņĄ£ļīĆļ¬©ņØśļ╣äĒÖŹņłśļ¤ēĻ│╝ Ļ░Ćņן ņØ╝ņ╣śĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ļ╣äņ£Āļ¤ēļ▓ĢņØś RMSEļŖö 3.556ņ£╝ļĪ£ ņĄ£ļīĆļ¬©ņØśļ╣äĒÖŹņłśļ¤ēĻ│╝ņØś ņ£Āņé¼ņä▒ņØĆ QRMF(K=5)ļ│┤ļŗż ņ×æņĢśļŗż. ņØ┤Ļ▓āņØĆ ļ╣äņ£Āļ¤ēļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ ļ░®ļ▓Ģļ│┤ļŗż QRMFļź╝ ņØ┤ņÜ®ĒĢĀ ļĢī ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņ£ĀņČ£ Ļ▓ĮĒ¢źņä▒ņØä ļŹö ņĀüņĀłĒĢśĻ▓ī ļīĆĒæ£ĒĢĀ ņłś ņ׳ļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż.
QRMFļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņ£ĀņČ£ļ¤ē Ļ▓ĮĒ¢źņä▒ņØä ņĀüņĀłĒĢśĻ▓ī Ēæ£ĒśäĒĢĀ ņłś ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢśņŚ¼ QRMF KĻ░ÆņØä ņČöņĀĢĒĢśņśĆļŗż. ļ¬©ļōĀ ņŚ░ļÅä ļ░Å ņ£ĀņŚŁņØä ļČäņäØĒĢ£ Ļ▓░Ļ│╝ ņ£ĀņŚŁņŚÉ ļö░ļØ╝ KĻ░ÆņØ┤ ļ│ĆļÅÖĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņé¼ļ®┤ Ļ▓Įņé¼, ņ╣©Ēł¼ņä▒, ĻĖ░ņĀĆņ£Āļ¤ē ļō▒Ļ│╝ Ļ░ÖņØĆ ņ£ĀņŚŁ ĒŖ╣ņä▒ņØ┤ ņ£ĀņŚŁļ¦łļŗż ļŗżļź┤ļ»ĆļĪ£ KĻ░ÆņØ┤ ļ│ĆĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļ│┤ņĢśļŗż. ĒĢśņ¦Ćļ¦ī KĻ░ÆņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ ņĄ£ļīĆņ£ĀņČ£ļ¤ēļÅä ņ”ØĻ░ĆĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņĄ£ļīĆ KĻ░Æņ£╝ļĪ£ ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒĢĀ ņłś ņ׳ļŗżĻ│Ā ĒīÉļŗ©ĒĢśņśĆļŗż. ņČöņĀĢ Ļ▓░Ļ│╝ 2013ļģä ņ×ÉļŻīņØś 27ļ▓ł ņ£ĀņŚŁ(4786.1 km2)ņŚÉņä£ 5.298ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņĄ£ļīĆ KĻ░ÆņØ┤ ļ░£ņāØĒĢśņśĆļŗż. ņØ┤ļĢī ņ£ĀņČ£ļ¤ēņØĆ 9308.94 m3/sļĪ£ ļ╣äĒÖŹņłśļ¤ēņ£╝ļĪ£ ļ│ĆĒÖśĒĢśņśĆņØä ļĢī 7 mm/hļĪ£ ļéśĒāĆļé¼ļŗż. ņĄ£ĻĘ╝ ĻĖ░ņāüņØ┤ļ│Ć Ēśäņāüņ£╝ļĪ£ ĻĄŁņ¦Ćņä▒ ĒśĖņÜ░Ļ░Ć ņ”ØĻ░ĆĒĢśļŖö ņČöņäĖņØ┤ļ®░ ņ£ĀņŚŁļ®┤ņĀüĻ│╝ ļ╣äĒÖŹņłśļ¤ēņØĆ power law Ļ┤ĆĻ│ä(Kim et al., 2017)ļź╝ Ļ░Ćņ¦ĆĻ│Ā ņ׳ņ£╝ļ»ĆļĪ£ ņ£ĀņŚŁļ®┤ņĀüņØ┤ ņ×æņĢäņ¦łņłśļĪØ ņĄ£ļīĆņ▓©ļæÉņ£Āļ¤ēņØś ļ░£ņāØ Ļ░ĆļŖźņä▒ņØ┤ ļåÆņĢäņ¦ĆļŖö Ļ▓āņØĆ ņé¼ņŗżņØ┤ļŗż. ļö░ļØ╝ņä£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØĆ QRMF(K=5.298)ļĪ£ ņČöņĀĢĒ¢łņ£╝ļ®░, ņČöņĀĢĒĢ£ Ļ▓░Ļ│╝ļŖö Table 3Ļ│╝ Ļ░Öļŗż. ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁ 6661.5 km2ņŚÉ ļīĆĒĢ┤ņä£ 10874.53 m3/sņØś ņĄ£ļīĆņ£ĀņČ£ļ¤ēņØ┤ ļ░£ņāØĒĢśņśĆņ£╝ļ®░, ņØ┤Ļ▓āņØĆ 5.88 mm/hņØś Ļ░ĢņÜ░Ļ░Ć ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁ ņĀäņ▓┤ņŚÉ ļé┤ļ”░ Ļ▓āĻ│╝ Ļ░ÖņØĆ ņ¢æņØ┤ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņŚÉ ļīĆĒĢ┤ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢśņŚ¼ ņāØņä▒ĒĢ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁ ņ£Āļ¤ē ņ×ÉļŻīņØś ņĀüņÜ® Ļ░ĆļŖźņä▒ Ļ▓ĆĒåĀņÖĆ QRMFļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒĢśļŖö ļ░®ņĢłņØä ņĀ£ņĢłĒĢśņśĆļŗż. ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś 2008~2017ļģäņŚÉ ļīĆĒĢ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņé░ņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ ņĄ£ļīĆ 75Ļ░£ ņ£ĀņŚŁņØä ņåīĻĘ£ļ¬©ļĪ£ ļČäĒĢĀĒĢśņŚ¼ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢśņśĆņ£╝ļ®░, ņāØņä▒ĒĢ£ ņ£Āļ¤ē ņ×ÉļŻīļź╝ ņ£ĀņŚŁĻ│╝ ņ▒äļäÉņØś ĒÖŹņłśņČöņĀüļ░®ļ▓Ģ(Flood Routing) Ļ┤ĆĻ│äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ü ņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņČöņČ£ĒĢ£ ļŗżņØī ļ╣äĒÖŹņłśļ¤ē ņ×ÉļŻīļĪ£ ļ│ĆĒÖśĒĢśņśĆļŗż. ļ╣äĒÖŹņłśļ¤ēĻ│╝ ņ£ĀņŚŁļ®┤ņĀüņØś Ļ┤ĆĻ│äņÖĆ ĒŖ╣ņä▒ņØä ļČäņäØĒĢśņśĆņ£╝ļ®░, QRMFņÖĆ ļ╣äĻĄÉļź╝ ĒåĄĒĢ┤ ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņĀäļ¦ØĒĢśņśĆļŗż. ĻĘĖ Ļ▓░Ļ│╝ļź╝ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņĀĢļ”¼ĒĢśņśĆļŗż.
ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢśņŚ¼ ņāØņä▒ĒĢ£ ņ£ĀņČ£ņ×ÉļŻīļŖö ņĀäņ▓┤ņĀüņ£╝ļĪ£ Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīņÖĆ ļ╣äņŖĘĒĢśĻ▓ī ļ¬©ņØśļÉśņŚłņ£╝ļéś ĻĖ░ņĀĆņ£Āļ¤ēņØä Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖņĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņ┤łĻĖ░ņŗ£Ļ░äņŚÉņä£ Ļ│╝ņåīĒÅēĻ░ĆĒĢśļŖö Ļ▓ĮĒ¢źņØ┤ ļéśĒāĆļé¼ļŗż. ņ£ĀņŚŁļ®┤ņĀüņØ┤ ņ╗żņ¦łņłśļĪØ ļ╣äĒÖŹņłśļ¤ē ļČäĒżĻ░Ć ņóüņĢäņ¦Ćļ®░, ņ£ĀņŚŁļ®┤ņĀü ļīĆļ╣ä ļ╣äĒÖŹņłśļ¤ēņØ┤ ņ×æņĢäņ¦ĆļŖö power law Ļ┤ĆĻ│äĻ░Ć ņä▒ļ”ĮĒĢśņśĆļŗż. ļśÉĒĢ£, ņ£ĀņŚŁ ņČ£ĻĄ¼ ņ¦ĆņĀÉņØĖ ņČ®ņŻ╝ļīÉņŚÉņä£ NSE ĻĖ░ņżĆņØä ļ¦īņĪ▒ĒĢśņŚ¼ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīĻ░Ć Ļ┤ĆņĖĪņ£ĀņČ£ņ×ÉļŻīņÖĆ ņ£Āņé¼ĒĢśļŗżļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż. ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņŚÉ ļīĆĒĢ┤ņä£ ņ£ĀņŚŁļ®┤ņĀüņØ┤ ļäōņ¢┤ņ¦łņłśļĪØ ņ▓©ļæÉļ░£ņāØņŗ£Ļ░äņØ┤ ņ¦ĆņŚ░ļÉśļŖö ņŗżņĀ£ ņ£ĀņŚŁņØś ĒŖ╣ņä▒Ļ│╝ ņ£Āņé¼ĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ļö░ļØ╝ņä£ ņ£ĀņČ£ņ×ÉļŻī Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓Ģņ£╝ļĪ£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ņé░ņČ£ĒĢśļŖö ļ░®ļ▓ĢņØĆ ņĀüĒĢ®ĒĢśņśĆņ£╝ļ®░, ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻī ņāØņä▒ Ļ░ĆļŖźņä▒ ļ░Å ĒÖ£ņÜ® Ļ░ĆļŖźņä▒ņØ┤ ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż.
QRMF ļ╣äĒÖŹņłśļ¤ēĻ│╝ ļ╣äņ£Āļ¤ēļ▓ĢņŚÉ ļīĆĒĢ┤ Ēö╝ņ¢┤ņŖ© ņāüĻ┤ĆĻ│äņłśļĪ£ ĒÅēĻ░ĆĒĢ£ Ļ▓░Ļ│╝ ļ¬©ļæÉ ļ¬©ņØśļ╣äĒÖŹņłśļ¤ēĻ│╝ ņāüĻ┤ĆĻ┤ĆĻ│äĻ░Ć ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. RMSEļĪ£ ĒÅēĻ░ĆĒĢ£ Ļ▓░Ļ│╝ ļ╣äņ£Āļ¤ēļ▓Ģļ│┤ļŗż QRMFļź╝ ņØ┤ņÜ®ĒĢ£ ļ░®ļ▓ĢņŚÉ ļŹö ņØ╝ņ╣śĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļéś ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ĒÖŹņłśļ¤ē ņČöņĀĢņØĆ ļ╣äņ£Āļ¤ēļ▓Ģļ│┤ļŗż QRMFļź╝ ņØ┤ņÜ®ĒĢ£ ļ░®ļ▓ĢņØ┤ ļŹö ņĀüĒĢ®ĒĢśņśĆļŗż. ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś KĻ░ÆņØĆ QRMF(K=5.298)ļĪ£ ņé░ņČ£ļÉśņŚłņ£╝ļ®░, ņé░ņČ£ĒĢ£ KĻ░Æņ£╝ļĪ£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒĢĀ ņłś ņ׳ņŚłļŗż.
QRMFļĪ£ ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņØś ĒÖŹņłśļ░£ņāØĻ░ĆļŖźņä▒ņØä ņČöņĀĢĒĢĀ ņłś ņ׳ņŚłņ¦Ćļ¦ī, ņØ┤ļź╝ ņĀłļīĆņĀü ĻĖ░ņżĆņ£╝ļĪ£ ĒÖ£ņÜ®ĒĢśĻĖ░ņŚÉ ļŗżņåī ļ¼┤ļ”¼Ļ░Ć ņ׳ņØä ņłś ņ׳ļŗż. ĻĘĖļ¤¼ļéś ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņĀ£ņŗ£ĒĢ£ QRMF ĒÖŹņłśļ¤ē ņČöņĀĢļ░®ļ▓ĢĻ│╝ ļŗżļźĖ ĒÖŹņłśļ¤ē ņČöņĀĢļ░®ļ▓ĢņØś ņĪ░ĒĢ®ņ£╝ļĪ£ ĒÖŹņłś ļ░£ņāØ Ļ░ĆļŖźņä▒ņØś ņĀĢĒÖĢļÅäļź╝ ļŹö Ē¢źņāüĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņāØĻ░üĒĢ£ļŗż. ņČ®ņŻ╝ļīÉ ņ£ĀņŚŁņŚÉ ļīĆĒĢ┤ Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓Ģņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ļ¬©ņØśĒĢĀ ņłś ņ׳ņŚłļŹś Ļ▓āņ▓śļ¤╝ ļŗżļźĖ ņ£ĀņŚŁņŚÉņä£ļÅä Ļ│ĄĻ░äĒÖĢņןļ░®ļ▓Ģņ£╝ļĪ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻīļź╝ ļ¬©ņØśĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ļ│┤ņØ┤ļ®░, ļŗżņ¢æĒĢ£ ļ»ĖĻ│äņĖĪņ£ĀņŚŁņØś ņ£ĀņČ£ņ×ÉļŻī ļČäņäØņŚÉ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ņĢäņÜĖļ¤¼ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ£ĀņČ£ņ×ÉļŻī ņżæņŗ¼ņ£╝ļĪ£ ņ¦äĒ¢ēļÉÉņ¦Ćļ¦ī ņČöĒøäņŚÉ Ļ░ĢņÜ░ņØś Ļ│ĄĻ░äļČäĒżļź╝ Ļ│ĀļĀżĒĢ£ ĒÖŹņłśņ£ĀņČ£ņ×ÉļŻīņØś ņāØņä▒ņ£╝ļĪ£ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņØś ĒÆłņ¦łņØä Ē¢źņāüĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢśļŖö ļ░öņØ┤ļ®░, RMSE ņØ┤ņÖĖņØś IOA, MBD, PBIAS ļō▒ņØś ļ¬©ņØśņ×ÉļŻī Ļ▓Ćņ”Ø ļ░®ļ▓ĢņØä ļ│æĒ¢ēĒĢśņŚ¼ ļ¬©ņØśņ£ĀņČ£ņ×ÉļŻīņØś ņŗĀļó░ļÅäļź╝ ļåÆņØ╝ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ļ│┤Ļ│Ā ņ׳ļŗż.
Ļ░Éņé¼ņØś ĻĖĆ
ļ│Ė ņŚ░ĻĄ¼ļŖö 2017ļģä ņĀĢļČĆ(ĻĄÉņ£ĪĻ│╝ĒĢÖĻĖ░ņłĀļČĆ)ņØś ņ×¼ņøÉņ£╝ļĪ£ ĒĢ£ĻĄŁņŚ░ĻĄ¼ņ×¼ļŗ©ņØś ņØ┤Ļ│ĄĒĢÖ Ļ░£ņØĖĻĖ░ņ┤łņŚ░ĻĄ¼ņ¦ĆņøÉņé¼ņŚģņØś ņ¦ĆņøÉņØä ļ░øņĢä ņłśĒ¢ēļÉ£ Ļ▓āņ×ä(NRFŌĆÉ2017R1D1A3B03033585). ņĀĆļźś ĒĢ©ņłś ļ¬©ĒśĢņØä ņĀ£Ļ│ĄĒĢśņŚ¼ ņŻ╝ņŗĀ ņłśņ×ÉņøÉĻ│Ąņé¼ ļ¼╝Ļ┤Ćļ”¼ņä╝Ēä░ņŚÉ Ļ░Éņé¼ļō£ļ”Įļŗłļŗż.
Table┬Ā1
Information of Each Event
Table┬Ā2
Estimation Results for Pearson Correlation Coefficient and RMSE in Choongju Watershed
Table┬Ā3
Possible Flood Occurrences at Choongju Dam Watershed Using QRMF(K=5.298)
References
Bae, DH, and Chung, IM (2000) Development of stochastic-dynamic channel routing model by storage function method. Journal of Korea Water Resources Association, Vol. 33, No. 3, pp. 341-350.

Chae, BS, Choi, SJ, Ahn, JH, and Kim, TW (2018) Estimation of flood quantile in ungauged watersheds for flood damage analysis based on flood index of natural flow. Journal of the Korean Society of Civil Engineers, Vol. 38, No. 1, pp. 175-182.

Chung, G, Park, HS, Sung, JY, and Kim, HJ (2012) Determination and evaluation of optimal parameters in storage function method using SCE-UA. Journal of Korea Water Resources Association, Vol. 45, No. 11, pp. 1169-1186.

Goswami, M, OŌĆÖconnor, KM, and Bhattarai, KP (2007) Development of regionalisation procedures using a multi-model approach for flow simulation in an ungauged catchment. Journal of Hydrology, Vol. 333, No. 2ŌĆō4, pp. 517-531.

Horton, R (1932) Drainage basin characteristics. Eos Transactions American Geophysical Union, Vol. 13, pp. 350-361.

Horton, R (1945) Erosional development of streams and their drainage basins: Hydrophysical approach to quantitative morphology. Geological Society of America Bulletin, Vol. 56, No. 3, pp. 275-370.

Hyndman, RJ, and Koehler, AB (2006) Another look at measures of forecast accuracy. International Journal of Forecasting, Vol. 22, No. 4, pp. 679-688.

Kim, BJ, Kawk, JW, Lee, JH, and Kim, HS (2008) Calibration and estimation of parameter for storage function model. Journal of Korean Society of Civil Engineers, Vol. 28, No. 1B, pp. 21-32.

Kim, NW, Jung, Y, and Lee, JE (2013) Spatial extension of runoff data in the applications of a lumped concept model. Journal of Korea Water Resources Association, Vol. 46, No. 9, pp. 921-932.

Kim, NW, and Shin, MJ (2017) Experimental study of rainfall spatial variability effect on peak flow variability using a data generation method. Journal of Korea Water Resources Association, Vol. 50, No. 6, pp. 359-371.

Kim, YI, Seo, SB, and Kim, YO (2018) Development of a hybrid regionalization model for estimation of hydrological model parameters for ungauged watersheds. Journal of Korea Water Resources Association, Vol. 51, No. 8, pp. 677-686.

Kimura, T (1961). Storage function methods for flood routing. Research Institute of Japan Civil Engineering, p 89-96. p 203-209.

Korea River Association (2016). Chapter 02: Investigation on the frequency of domestic stream design. Determination of proper frequency design of Local Stream in Chungcheongnam-do province. Retrieved from http://www.prism.go.kr/homepage/entire/retrieveEntireDetail.do?research_id=6440000-201700039.

Kovacs, Z (1988). Regional maximum flood peaks in Southern Africa. Technical Report No. 137. Department of Water Affairs, Pretoria, Republic of South Africa.

Kwon, KD, Lee, JH, Kang, MJ, and Jee, HK (2014) Effect of estimation for time of concentration on the design flood. Journal of Wetlands Research, Vol. 16, No. 1, pp. 125-137.

Moriasi, DN, Arnold, JG, Van Liew, MW, Bingner, RL, Harmel, RD, and Veith, TL (2007) Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Transactions of the ASABE, Vol. 50, No. 3, pp. 885-900.

Nash, JE, and Sutcliffe, JV (1970) River flow forecasting through conceptual models part I: A discussion of principles. Journal of Hydrology, Vol. 10, No. 3, pp. 282-290.

Nassif, SH, and Wilson, EM (1975) The influence of slope and rain intensity on runoff and infiltration. Hydrological Sciences Journal, Vol. 20, No. 4, pp. 539-553.

Park, JY, Shin, CD, and Lee, JS (2004) A study on the critical duration of design rainfall in midsize catchment. Journal of Korea Water Resources Association, Vol. 37, No. 9, pp. 695-706.

Pegram, G, and Parak, M (2004) A review of the regional maximum flood and rational formula using geomorphological information and observed floods. Water SA, Vol. 30, No. 3, pp. 377-392.

Pontius, R, Thontteh, O, and Chen, H (2008) Components of information for multiple resolution comparison between maps that share a real variable. Environmental and Ecological Statistics, Vol. 15, No. 2, pp. 111-142.

Ritter, A, and Mu├▒oz-Carpena, R (2013) Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. Journal of Hydrology, Vol. 480, No. 1, pp. 33-45.

Singh, VP (1997) Effect of spatial and temporal variability in rainfall and watershed characteristics on stream flow hydrograph. Hydrological Processes, Vol. 11, pp. 1649-1669.

Sivapalan, M, Takeuchi, K, Franks, SW, Gupta, VK, Karambiri, H, Lakshmi, V, et al (2003) IAHS decade on predictions in ungauged basins (PUB), 2003ŌĆō2012 Shaping an exciting future for the hydrological sciences. Hydrological Sciences Journal, Vol. 48, No. 6, pp. 857-880.

Strahler, AN (1952) Hypsometric (Area-altitude) analysis of erosional topology. Geological Society of America Bulletin, Vol. 63, pp. 1117-1142.

Strahler, AN (1964). Quantitative geomorphology of drainage basins and channel networks. In: Chow VT, ed. Handbook of Applied Hydrology. p 439-476. New York: McGraw-Hill.

Tofiq, FA, and Guven, A (2014) Prediction of design flood discharge by statistical downscaling and general circulation models. Journal of Hydrology, Vol. 517, No. 19, pp. 1145-1153.