|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 19(4); 2019 > Article |
|
Abstract
To estimate the serviceability and safety of high-rise buildings under various dynamic-loading conditions, a reliable analytical model is needed. In this study, an analytical-model calibration process is proposed to obtain a reliable analytical model for high-rise buildings. A high-rise residential complex building is selected as a test bed, and the natural frequency and mode shape are derived from vibration measurement. On the basis of the measurement, analytical-model calibration using artificial neural network is performed to update the initial analytical model. Through this process, the calibrated analytical model exhibits remarkable coherence with the measurement at the principal natural frequency and mode shape at an acceptable tolerance level.
요지
다양한 하중 시나리오에 대한 초고층 건축물의 사용성 및 안전성 평가를 위해서는 신뢰성 있는 해석 모델의 생성이 필요하다. 본 연구에서는 초고층 건축물의 신뢰성 있는 해석 모델 생성을 위한 일련의 Calibration Process를 제안한다. 이에 초고층 주거복합 구조물을 Test Bed로 선정하여 상시 상태에서의 진동 계측을 통한 고유진동수 및 모드형상을 도출하였고, 인공신경망 기반 초기 해석 모델의 교정을 수행하였다. 이러한 과정을 통해 생성한 해석 모델은 주요 고유진동수 및 모드형상에 대해 실제 대상 건축물과 허용 오차 범위 내 충분히 유사한 결과를 제시하였다.
건축물의 고층화 현상이 가속화됨에 따라 풍하중, 지진하중과 같은 동적 횡하중에 의한 사용성 및 안전성 문제가 빈번히 발생하고 있으며, 이를 해결하기 위해 초고층 건축물의 상태를 평가하고 관리하는 모니터링 기술인 구조 건전도 모니터링(Structural Health Monitoring) 연구가 활발히 수행되고 있다. 다양한 하중 시나리오에 대해 초고층 건축물의 사용성 및 안전성을 예측하고 평가하기 위해서는 실제 대상 건축물과 유사하게 거동하는 신뢰성 있는 해석 모델의 생성이 필요하다. 그러나 구조설계를 위한 해석 모델은 수많은 가정 사항들을 포함하고 있어 실제 대상 건축물의 동적 거동 및 세부적인 사항에 대해서는 차이점을 지닌다. 이에 신뢰성 있는 해석 모델 생성을 위해 실제 대상 건축물의 동특성 분석을 수행하고, 이를 해석 모델과 비교하여 해석 모델의 동특성을 실제 대상 구조물과 유사하게 교정하는 Calibration의 과정을 수행하게 된다.
구조물의 동특성 추출을 위한 모드 분석(Modal Analysis) 방법으로는 크게 Experimental Modal Analysis (EMA)와 Operational Modal Analysis (OMA)가 있다. 각각의 분석 방법은 외력을 알고 있는 상태에서 대상 구조물에 외력을 가하여 외력과 구조물 응답 간 관계를 파악하여 모드 분석을 수행하는 방법(Forced Vibration Measurement)과, 대상 구조물의 응답만을 이용하여 모드 분석을 수행하는 방법(Output-only Measurement)으로 대별된다. EMA를 수행하기 위해서는 대상 구조물에 강제 변위를 가하여 자유 진동(Free Vibration)을 발생시키거나, 임팩트 해머(Impact Hammer) 혹은 가진기(Exciter)를 통해 대상 구조물을 가진하게 된다. 그러나 실제 건축물 및 교량과 같은 대형 구조물의 동특성을 추출하기 위해 대상 구조물에 특정한 외력을 가하는 것은 현실적으로 어려우며, 이를 위해 상시 상태에서의 대상 구조물의 응답을 계측하여 동특성을 분석하는 방법인 OMA를 수행할 수 있다. OMA는 입력하중을 백색 소음(White Noise)으로 가정하여 Reference 계측 응답과 그 외의 계측 응답 간의 Cross-power Spectrum으로부터 시스템의 동특성을 추출하는 기법으로(Pierro et al., 2009), EMA와 비교하였을 때 상시 상태에서의 계측된 응답만으로 대상 구조물의 동특성을 추출할 수 있다는 점에서 장점을 가진다.
실제 건축물의 동특성을 추출하기 위해 가속도계, 변위계와 같은 계측기를 이용하여 상시 상태에서의 대상 건축물의 미진동을 계측하고, 계측 데이터로부터 구조물의 동특성인 고유진동수, 모드형상, 모드 감쇠비를 추출하는 일련의 과정을 시스템 식별이라고 한다. 시스템 식별로부터 추출된 동특성은 대상 건축물의 상태 예측 및 손상 탐지 등 구조 건전도 모니터링을 위한 자료로 활용될 수 있다(Salawu, 1997). 이에 상시 상태에서의 미진동을 계측하여 초고층 건축물의 시스템 식별 및 모니터링을 수행하는 연구가 수행되고 있다(Shi et al., 2012; Jeong et al., 2013; Heo et al., 2017; Kim et al., 2018; Moon, 2018).
Jeong et al. (2013)은 국내 다양한 소재지에 위치한 고층 건물들에 가속도계를 설치하여 상시 진동 계측을 수행하고, Stochastic Subspace Identification 기법을 이용하여 고유진동수 및 감쇠비를 분석하였다. Heo et al. (2017)은 부산 소재의 초고층 건축물을 대상으로 상시 및 강풍시의 가속도 응답을 모니터링하였으며, 계측 응답으로부터 다양한 시스템 식별 기법 중 Stochastic Subspace Identification, Random Decrement Technique, Frequency Domain Decomposition 기법을 사용하여 고유진동수를 비교 및 분석하였다. Shi et al. (2012)은 약 492 m 높이의 Shanghai World Financial Center (SWFC) 시스템 식별을 위해 상시 진동 및 자유 진동 계측을 수행하여 가속도 응답을 취득하였다. 시스템 식별을 위해 Half-power Bandwidth, Random Decrement Technique, Hilbert-Huang Transform 기법이 사용되었으며, 시스템 식별 기법에 대한 동특성 결과를 비교 및 분석하였다.
한편, 현장 계측 결과와 해석 모델의 동특성을 Calibration하기 위한 연구가 수행되고 있다. Skolnik et al. (2006)은 15층 철골 모멘트골조를 대상으로 상시 진동 및 지진 시 진동 계측을 수행하여 시스템 식별을 수행하였고, 초기 해석 모델로부터 강성 및 질량을 변경하여 계측에 의한 동특성과 해석 모델의 동특성에 대한 차이를 최적화 알고리즘을 통해 최소화하는 강성 및 질량을 추정하였다. Kim et al. (2009)은 서울 및 부산 소재의 고층 건물들을 대상으로 상시 및 강풍시의 가속도 응답을 모니터링하였고, Frequency Domain Decomposition 기법을 이용하여 고유진동수를 추출하였다. 이를 초기 해석 모델과 비교하고, 해석 모델로부터 Beam-end-offset, 슬래브 요소 모델링, 비구조 벽체 모델링, 탄성계수를 변경하여 Calibration을 수행하였다.
기존의 선행 연구들은 실제 건축물을 대상으로 현장 계측을 수행하고, 다양한 시스템 식별 기법으로부터 도출한 동특성의 비교 및 분석 결과만을 제시하고 있다. 계측 결과만을 이용하여 대상 건축물의 모니터링을 수행하기에는 부재의 개수, 현장 조건의 불확실성과 같은 현실적인 측면에서 연구가 미흡한 실정이다. 이에 신뢰성 있는 해석 모델을 생성하여 동적 하중에 대한 상세 해석으로부터 대상 건축물의 사용성 및 안전성을 평가할 수 있으나, 초고층 건축물을 대상으로 해석 모델을 검토하고 다양한 변수로부터 해석 모델의 Calibration을 수행한 연구 또한 미흡한 실정이다.
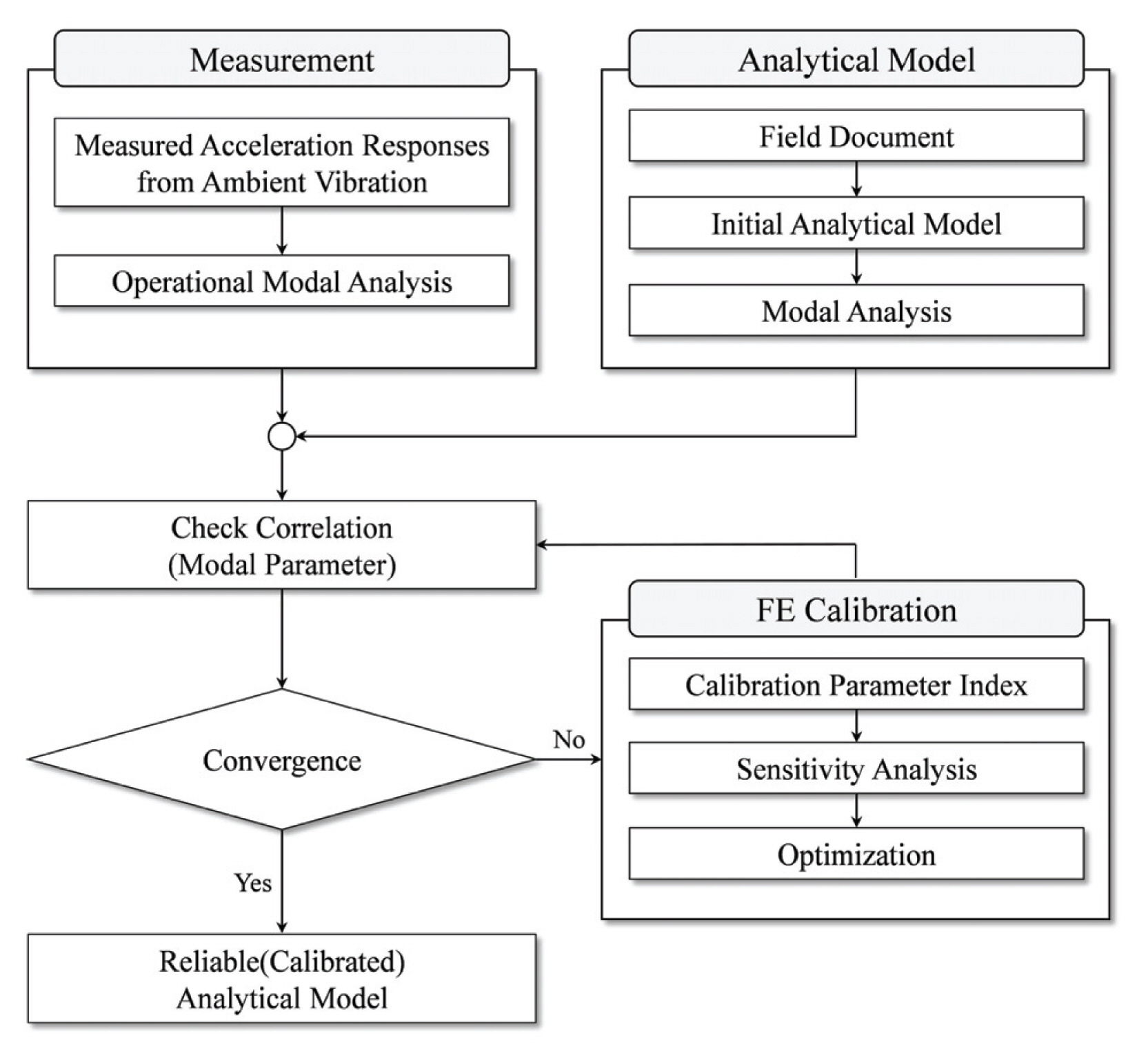
본 연구에서는 초고층 건축물의 신뢰성 있는 Analytical Model을 생성하기 위해 대상 건축물의 현장 계측 및 계측 기반 시스템 식별을 수행하고, 이를 초기 해석 모델과 비교하여 Calibration을 수행한다. Calibration을 수행하기 위해 동특성 인자인 Calibration Parameter를 선정하여 초기 해석 모델로부터 동특성(고유진동수 및 모드형상)에 대한 민감도 분석을 수행한다. 본 연구는 인공신경망을 이용하여 민감도 분석으로부터 도출된 Calibration Parameter와 해석 모델의 동특성 정보 간의 관계를 구축하고, 학습된 네트워크로부터 실제 대상 건축물의 동특성 정보를 입력하였을 때의 Calibration Parameter를 예측한다. 이를 해석 모델에 반영하고 현장 계측 결과와 비교 및 분석함으로써 초고층 건축물의 신뢰성 있는 Analytical Model을 생성하고자 한다. 본 연구에서 수행한 Calibration Process는 Fig. 1과 같이 요약된다.
계측 데이터에 기반하여 초고층 건축물의 Analytical Model Calibration을 수행하고, 신뢰성 있는 해석 모델을 생성함으로써 다양한 하중 시나리오에 대한 초고층 건축물의 상태를 평가할 수 있다. 본 연구에서는 Test Bed를 선정하여 현장 계측을 수행하고, 이를 통해 신뢰성 있는 해석 모델을 생성하고자 한다. 이에 Test Bed 대상 건축물로 경기도에 위치한 약 200 m 높이의 초고층 주거복합 구조물을 선정하였다.
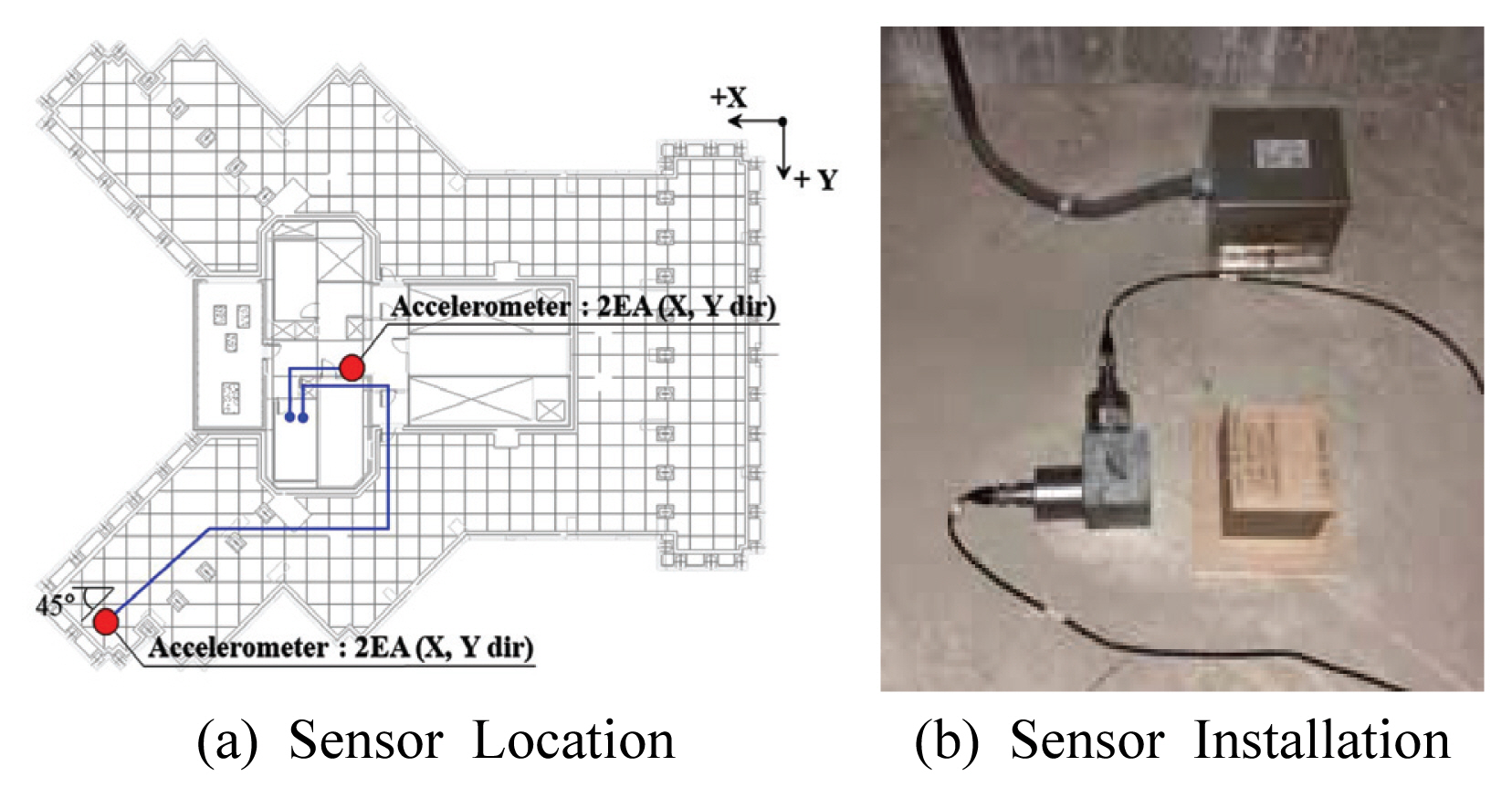
현장 계측을 통한 구조물의 동특성을 분석하기 위해서는 구조물의 동특성을 명확히 파악할 수 있는 계측 위치를 선정하는 것이 중요하다. 이에 본 연구에서는 건물의 유형, 높이, 현장 여건 등을 고려하여 최상층 및 최하층, 그리고 약 50 m, 110 m, 150 m 높이에 해당하는 기준층을 측정 기준층으로 선정하였으며, 추가적으로 지상 저층부 구조물이 해당 대상 건축물에 미치는 영향을 파악하기 위해 지상 1층 및 3층을 측정 기준층으로 선정하였다. 이로부터 대상 건축물의 비틀림 성분을 계측하기 위해 측정 기준층(총 7개소)의 코어 중앙부와 외곽부에 가속도계를 Fig. 2와 같이 2축 방향으로 배치하여 대상 건축물에 대한 수평 방향(X axis, Y axis) 가속도 응답을 취득하였다. 측정은 약 30분간 수행하였으며, 가속도계의 Sampling Rate는 1,024Hz로 설정하였다.
상대적으로 입력하중을 제어하기 어려운 건축물, 교량과 같은 대규모 구조물을 대상으로 대상 구조물의 미진동을 계측하고, 계측한 응답만으로 주파수 응답 함수(Frequency Response Function, FRF)를 구성하여 대상 구조물의 동특성을 추출하는 방법인 OMA을 적용할 수 있다. Eq. (1)과 같이 Reference로 선정한 계측 응답의 Auto-power Spectrum, 그리고 Reference 응답과 그 외의 계측 응답 간의 Cross-power Spectrum으로부터 주파수 응답 함수가 구성된다. 이러한 주파수 응답 함수의 Peak에 해당하는 주파수 대역으로부터 시스템의 고유진동수 및 모드형상을 추출할 수 있다.
여기서, {φ}h는 모드 벡터이며, {Q}h는 Output-only Reference 벡터이다.
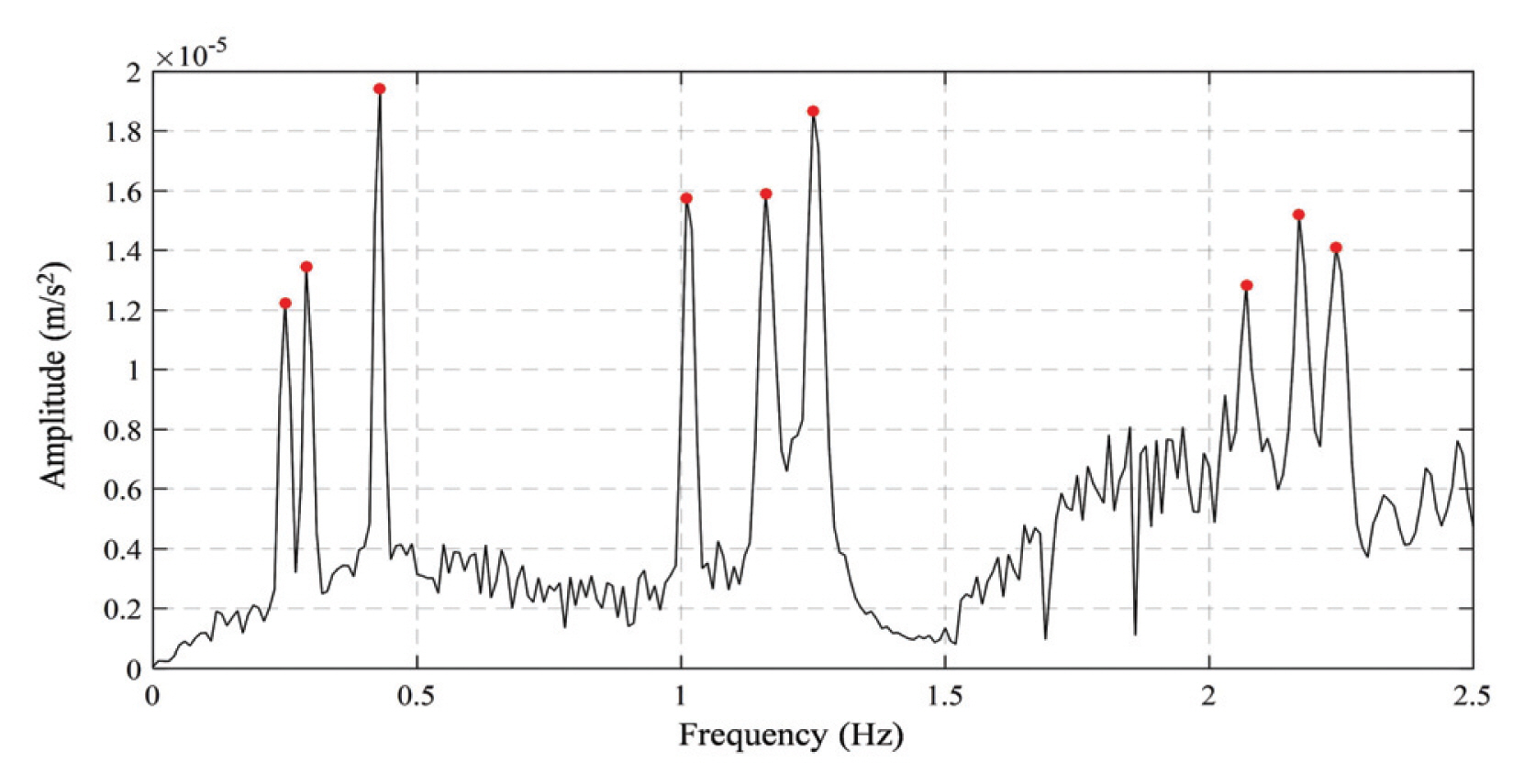
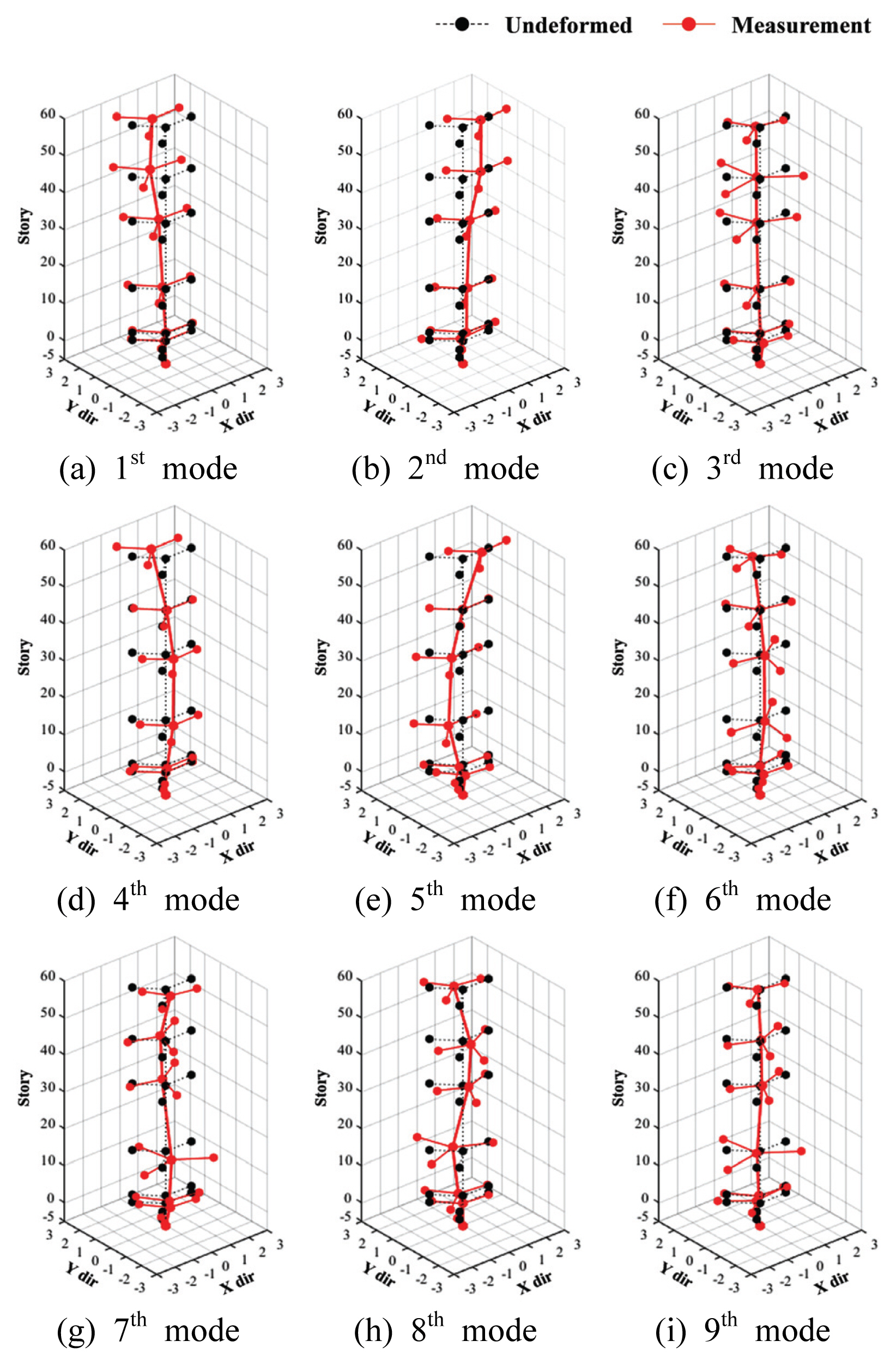
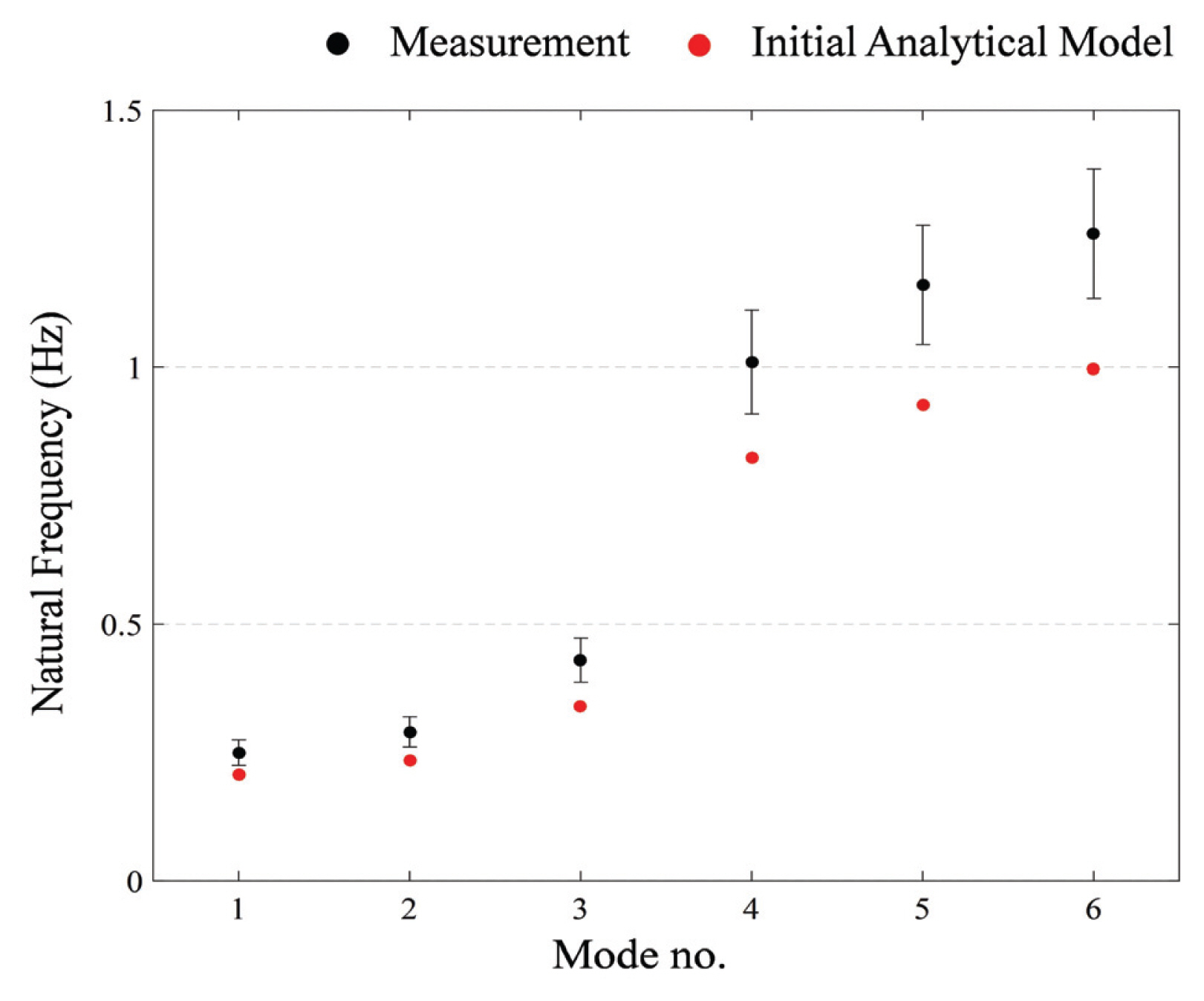
본 연구에서는 대상 건축물의 시스템 식별을 위해 상시 상태에서 측정된 기준층들의 가속도 응답으로부터 OMA를 수행하여 Fig. 3과 같이 Test Bed의 각 방향에 대한 1차 모드, 2차 모드, 그리고 3차 모드를 도출하였다. 약축 방향(Y axis)의 1차 모드는 0.25 Hz, 2차 모드는 1.01 Hz, 3차 모드는 2.07 Hz이며, 강축 방향(X axis)의 1차 모드는 0.29 Hz, 2차 모드는 1.16 Hz, 3차 모드는 2.17 Hz이다. 그리고 비틀림 방향(Torsion)의 1차 모드는 0.43 Hz, 2차 모드는 1.26 Hz, 3차 모드는 2.24 Hz이다. 각 방향에 대한 모드형상은 Fig. 4와 같다.
다양한 하중 시나리오에 대한 대상 구조물의 상태를 예측하고 평가하기 위해 해석 모델을 생성하고, 하중 시나리오에 대한 해석을 수행하게 된다. 이를 위해 실제 대상 건축물과 유사하게 거동하는 해석 모델이 필요하며, 이는 초기 설계된 해석 모델로부터 추출한 동특성과 실제 대상 건축물의 현장 계측으로부터 추출한 동특성 간의 차이를 비교한 뒤, 그 차이를 Calibration의 과정을 통해 최소함으로써 Correlation된 해석 모델을 생성하게 된다.
실제 대상 건축물과 유사하게 거동하는 해석 모델을 생성하기 위해 초기 해석 모델을 생성하게 된다. 초기 해석 모델은 구조 계산서 및 준공도면과 같은 현장 자료에 기초하여 생성되며, 이로부터 추출한 동특성, 즉 고유진동수 및 모드형상을 계측에 의한 동특성과 비교 및 분석하게 된다.
현장 자료에 의해 초기 설계된 해석 모델과 대상 건축물의 현장 계측에 의한 동특성의 차이는 대상 건축물의 전역적인 질량, 강성, 감쇠의 차이로부터 기인하며, 이는 실제 현장상황과 구조도서 간의 차이, 설계 및 해석을 위한 가정 사항, 시공 오차 등으로 인해 발생할 수 있다. 본 연구에서는 Geometry를 포함하여 강성, 하중, 지점 및 구속조건 등과 같은 사항들을 검토하고, 이러한 사항 중 영향력이 큰 사항들을 Calibration Parameter로 선정하여 인공신경망을 통해 산출한 변수 해를 해석 모델에 반영함으로써 Calibration을 수행하였다.
본 연구의 Test Bed 초기 해석 모델을 생성하기 위해 부재 일람표, 설계하중 일람표와 같은 현장 도서에 기반하여 모델링을 수행하였다. 해석 모델의 슬래브 요소(플랫 플레이트)는 지진하중 시나리오에 대한 비선형 해석을 수행하기 위해 유효보폭법(Effective-Beam Width method)을 적용하여 등가의 유효폭을 가지는 단순보로 입력하였다. 본 연구에서는 건축구조기준(2016)에 의거하여 슬래브의 유효 강성을 0.25Ig로 산정하였으며, 공동주택 성능기반 내진설계 지침(2017)에 의거하여 고정하중의 1.0배, 그리고 활하중의 0.25배를 대상 건축물의 질량으로 적용하였다.
현장 자료로부터 설계된 초기 해석 모델의 모드 해석을 수행하였으며, 해석 모델의 방향별 고유진동수는 Table 1과 같다. 모드의 방향성은 각 모드에서의 방향별 질량참여율 중 가장 지배적인 방향의 질량참여율로부터 판단할 수 있다. 또한 본 연구에서는 Calibration을 위한 관심 주파수를 해석 모델에서의 질량참여율로부터 선정하였으며, 각 방향의 질량참여율이 전반적으로 80% 수준이 되는 6차 모드까지를 관심 주파수로 선정하였다.
Test Bed 현장 계측 결과와 초기 해석 모델의 고유진동수를 비교하였을 때, 관심 주파수 대역 내 최소 17.4% ~ 최대 21.1%의 차이가 발생함을 확인하였다. 일반적으로 계측 결과와 해석 모델 간 Calibration을 수행함에 있어 두 시스템 간의 동특성을 10%의 오차 범위 내로 Correlation할 것을 권장하며(Brownjohn et al., 2001), Fig. 5를 통해 현장 계측 결과와 초기 해석 모델 간의 고유진동수 차이가 본 연구에서 목표하는 오차 범위인 10%를 초과함을 확인할 수 있다. 이에 본 연구에서는 오차 범위 내 실제 건축물과 해석 모델 간 고유진동수를 Correlation하기 위해 초기 해석 모델로부터 Calibration을 수행하였다.
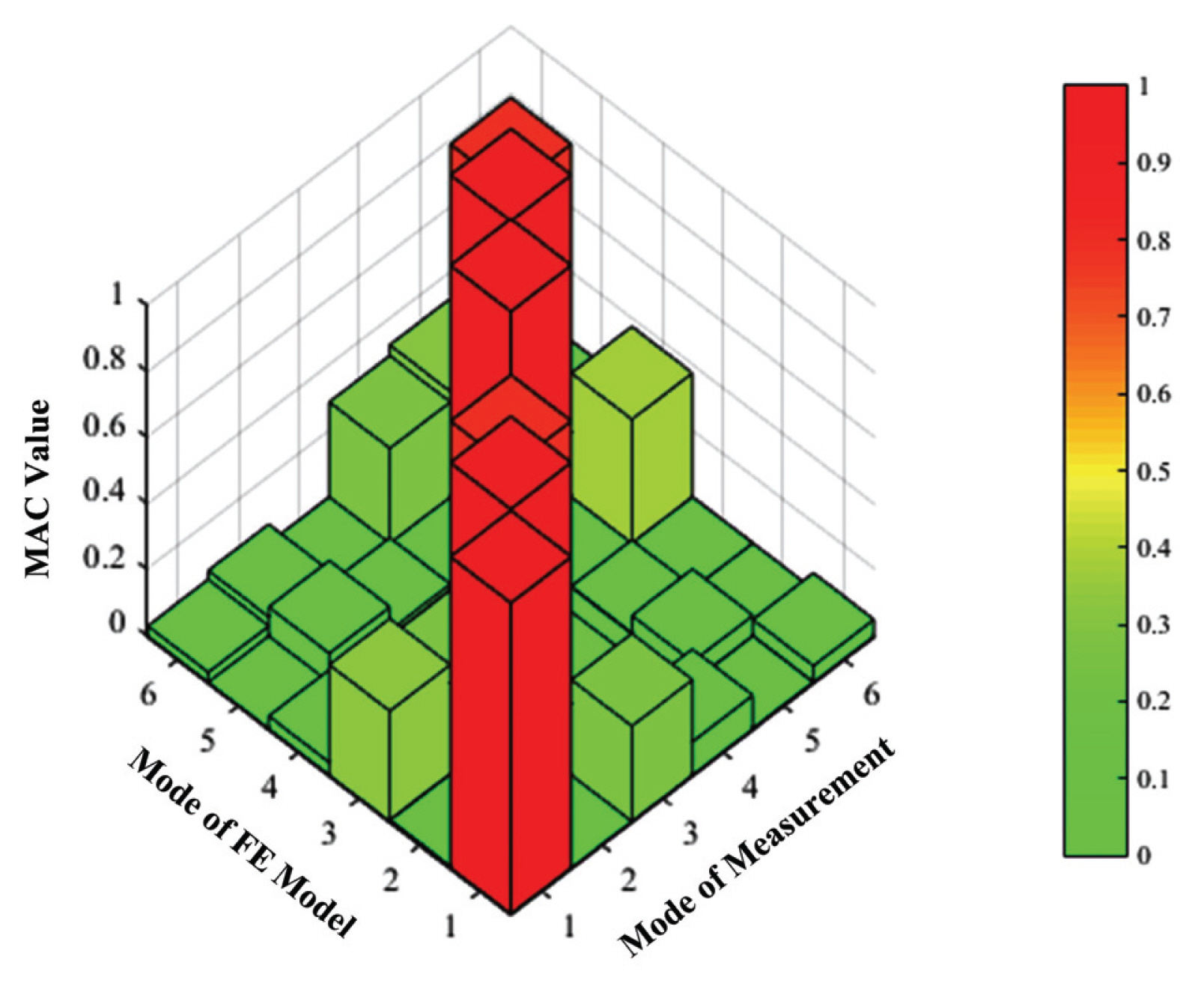
본 연구에서는 Modal Assurance Criterion (MAC)를 통해 Test Bed 현장 계측 결과와 해석 모델의 모드형상을 비교 및 분석하였다. MAC이란, 두 시스템 간의 모드형상을 정량적으로 평가하는 기법으로 모드형상의 유사성(Correspondence 혹은 Coherence)을 비교하는데 흔히 사용된다. MAC 값은 Eq. (2)와 같이 정규화된 스칼라 값으로 0 ~ 1의 값을 가지며, 일반적으로 MAC 값이 0.8 ~ 0.9 이상일 때 두 시스템 간 모드형상이 유사하다 혹은 잘 맞는다고 판단할 수 있다(Pastor et al., 2012; Olsen and Brincker, 2015).
여기서, φ A i φ B j
Test Bed 현장 계측 시 추출한 모드형상과 초기 해석모델의 모드형상의 MAC 값을 Fig. 6 및 Table 2와 같이 비교한 결과, X 방향과 Y 방향의 모드인 1차 모드, 2차 모드, 4차 모드, 5차 모드에 대한 MAC 값이 최소 0.94 ~ 최대 0.98임을 확인하였고, 이는 실제 대상 건축물의 모드형상과 초기 해석 모델의 모드형상이 거의 유사함을 의미한다. 또한, 비틀림 방향의 모드인 3차 모드 및 6차 모드에 대한 MAC 값은 약 0.79임을 확인하였고, 이는 실제 대상 건축물의 모드형상과 초기 해석 모델의 모드형상이 비교적 유사함을 의미한다.
본 연구에서는 초기 해석 모델의 동특성을 실제 대상 건축물의 동특성과 Calibration하기 위해 구조물의 동특성 인자인 강성 및 질량, 그리고 구속조건으로부터 Calibration Parameter를 선정하였고, Calibration Parameter의 최적 해로부터 해석 모델의 Calibration을 수행하였다. 즉, 구조물의 강성 및 질량, 그리고 구속조건을 일정 범위 내에서 변경하여 실제 대상 건축물의 동특성과 유사한 강성 및 질량, 그리고 구속조건 값을 찾는 것이 본 Analytical Model Calibration의 목적이며, 이를 위해 각각의 Calibration Parameter(강성, 질량, 구속조건) 그룹에 대한 민감도 분석(Sensitivity Analysis)을 수행하였다.
강성 변경이 대상 건축물의 동특성에 미치는 영향을 평가하기 위해 강성에 대한 민감도 분석을 수행하였다. 대상 건축물의 강성을 변경하기 위해 대상 건축물에서의 주요 구조 부재를 선정하여 이에 해당하는 재료의 탄성계수를 변경하였다. 이는 실제 대상 건축물과 해석 모델 간의 동적 거동을 전역적으로 Correlation하기 위함이다. 이에 주요 구조 부재는 기둥, 유효보, 코어 벽체, 벨트월 및 메가보, 그리고 인방보로 구성되며, 각 주요 구조 부재에 해당하는 재료는 기둥, 코어 벽체, 그리고 인방보의 경우 총 5그룹(C50, C45, C40, C35, C30), 유효보의 경우 총 2그룹(C35, C30), 그리고 벨트월 및 메가보의 경우 총 1그룹(C35 및 C30)으로 분류된다. 초기 해석 모델로부터 재료에 따라 분류된 주요 구조 부재의 탄성계수를 50%, 150%, 200%, 250%, 300% 순으로 변경하여 모드 해석을 수행하였고, 재료의 탄성계수, 즉 강성 변경에 따른 해석 모델별 고유진동수를 분석하였다.
본 연구에서는 공동주택 성능기반 내진설계 지침에 의거하여 고정하중의 1.0배, 그리고 활하중의 0.25배를 대상 건축물의 질량으로 적용하여 초기 해석 모델을 생성하였지만, 실제 건축물에 작용하는 활하중은 실용도 및 사용자와 물품의 중량과 같은 현장 상황에 따라 변경될 수 있다. 이러한 활하중의 변경, 즉 질량 변경이 대상 건축물의 동특성에 미치는 영향을 평가하기 위해 활하중의 질량 고려율에 대한 민감도 분석을 수행하였다. 이에 대상 건축물의 활하중을 질량으로 0%, 5%, 10%, 15%, 20% 순으로 변경하여 모드 해석을 수행하였고, 활하중의 질량 고려율에 따른 해석 모델별 고유진동수를 분석하였다.
본 연구에서는 초기 해석 모델을 생성함에 있어 지반과 건축물 간의 상관관계를 고려하기 위해 다른 주거복합 구조물과 연결되어 있는 지하층 구조물의 골조를 2 bay 수준으로 나누어 모델링을 수행하였다. 이러한 대상 건축물 외곽의 지하 구조물(지하 4층 ~ 지상 1층) 및 지상 저층부에 존재하는 부대시설 구조물(지상 2층 ~ 지상 3층)의 구속조건이 동특성에 미치는 영향을 평가하기 위해 구속조건 변경에 대한 민감도 분석을 수행하였다. 구속조건 변경을 위해 지하층 및 지상 저층부 경계 구간에 해당하는 절점에 수평 방향의 변위 자유도와 수직 방향의 회전 자유도에 대한 스프링 강성을 입력하였다. 이에 초기 해석 모델로부터 지하층 및 지상 저층부 경계 구간에 대해 스프링 강성을 10 kN/mm, 100 kN/mm, 1000 kN/mm, 10000 kN/mm, 100000 kN/mm 순으로 추가하여 모드 해석을 수행하였고, 구속조건 변경에 따른 해석 모델별 고유진동수를 분석하였다.
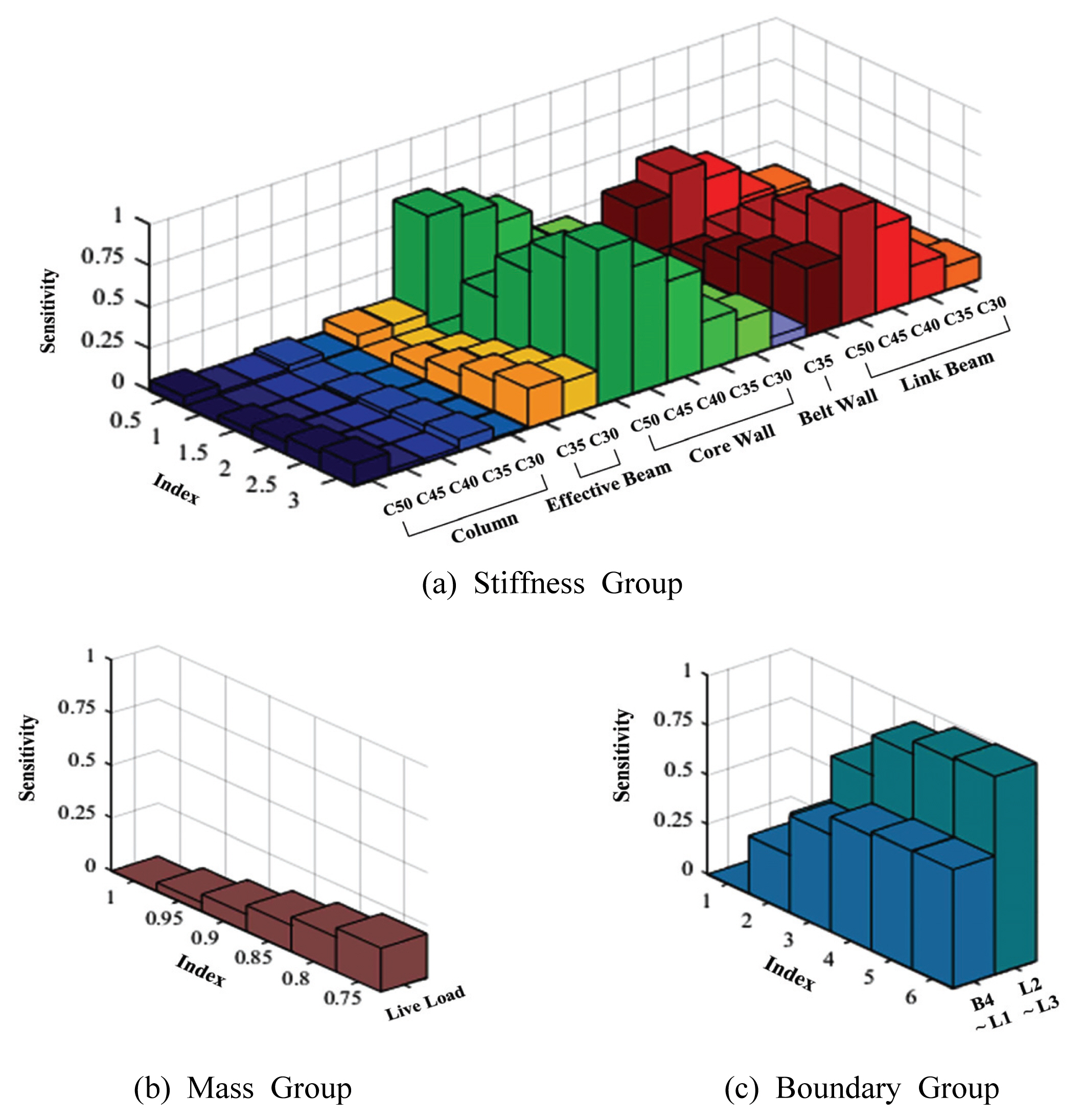
Calibration Parameter(강성, 질량, 구속조건) 그룹에 해당하는 각각의 변수들을 독립적으로 변경하고, 이에 대한 해석 모델의 고유진동수 변화를 분석함으로써 각 그룹에 대한 변수들이 해석 모델의 고유진동수에 미치는 영향을 확인할 수 있다. 이에 초기 해석 모델로부터 각 그룹에 대한 변수들의 값(Calibration Parameter Index)을 변경하였을 때의 고유진동수 변화율을 Figs. 7 및 8에 나타내었다. 여기서 Calibration Parameter Index란, 초기 해석 모델에서의 Calibration Parameter인 주요 구조 부재의 탄성계수, 활하중의 질량 고려율, 지하층 및 지상 저층부의 구속조건을 1.0(기준값)으로 설정하고, 변수 그룹의 증감률(scale factor)에 따라 강성 그룹의 경우 최소 0.5 ~ 최대 3.0, 질량 그룹의 경우 최소 0.75 ~ 최대 1.0, 구속조건의 그룹의 경우 최소 1.0 ~ 최대 6.0의 값을 갖도록 설정한 값이다. 예를 들어, 강성 그룹 중 C50에 해당하는 기둥 부재의 탄성계수를 50%로 고려했을 때의 C50 기둥 부재의 강성 변수 지표는 0.5이고 나머지 변수 지표는 1.0이다. 한편 질량 그룹의 경우, 활하중이 25% 고려되었을 때의 활하중 변수 지표는 1.0(기준값), 그리고 활하중이 0% 고려되었을 때의 활하중 변수 지표는 0.75이다.
Test Bed 강성 민감도 분석 결과, 병진 방향의 모드에 대해 코어 벽체와 기둥의 강성이 다른 주요 구조 부재 대비 동특성에 미치는 영향도가 큼을 확인하였고, 이러한 코어 벽체와 기둥 중 C50에 해당하는 부재가 대상 건축물의 동특성에 지배적인 영향을 미치는 것으로 확인되었다. 이는 대상 건축물의 지하층부터 지상 10층까지의 코어 벽체 및 기둥에 해당하는 부재로, 저층부 강성이 상층부 대비 동특성에 대한 민감도가 큼을 확인하였다. 한편, 비틀림 방향의 모드에 대해 코어 벽체와 인방보의 강성이 다른 주요 구조 부재 대비 동특성에 미치는 영향도가 큼을 확인하였다.
활하중의 질량 고려율의 경우, 병진 방향 및 비틀림 방향 모두 강성 및 구속조건 그룹 대비 동특성에 미치는 영향도가 상대적으로 낮음을 확인하였으며, 구속조건의 경우 지하층 대비 지상 저층부의 구속조건이 동특성에 미치는 영향도가 큼을 확인하였다.
본 연구에서는 민감도 분석을 통해 얻은 해석 모델의 동특성 결과를 DB화하고, 이를 인공신경망의 학습 데이터로 활용하여 Test Bed 현장 계측 결과와 해석 모델 간 Calibration을 수행한다.
본 연구에서는 각 변수 그룹의 민감도 분석으로부터 인공신경망을 이용하여 Calibration Parameter 중 최적 해를 산출하였다. 인공신경망이란 인간의 뇌 학습 방법을 모사한 수학적 모델로, 입력층(Input Layer), 은닉층(Hidden Layer), 그리고 출력층(Output Layer)으로 구성된다. 입력층의 노드를 통해 입력된 입력값은 연결강도(Weight)에 의해 가중되어 합산되며, 합산된 값은 활성화 함수에 의해 출력값을 출력한다. 인공신경망은 입/출력 데이터를 학습하여 네트워크를 형성하고, 형성된 네트워크에 기반하여 새로운 입력 데이터가 입력되었을 때 결과를 예측하여 출력한다. 입력값과 출력값 간의 관계를 반복적으로 학습하는 단계를 훈련(Training)이라고 하며, 훈련에 사용되지 않은 입력값을 통해 훈련된 네트워크의 성능을 실제 값과 비교하여 검증하는 단계를 검증(Validation)이라고 한다. 훈련 및 검증의 단계를 거쳐 우수한 성능을 가지는 네트워크를 형성한 뒤, 예측하고자 하는 입력값에 대한 결과를 예측하게 된다. 본 연구에서는 오류 역전파 신경망(Back Propagation Neural Network, BPNN)을 적용하여 Calibration 최적 해 탐색을 수행하였다.
본 연구에서는 대상 건축물의 Calibration 최적 해 탐색을 위해 Calibration Parameter와 해석 모델의 동특성 결과 간의 관계를 구축하였다. 이에 인공신경망의 입력값은 각 변수 그룹의 값(Calibration Parameter Index)을 변경하였을 때의 해석 모델의 고유진동수 및 모드형상이며, 출력값은 해당 해석 모델에 입력된 Calibration Parameter Index이다. 이에 Calibration Parameter Index의 값 변경에 따른 해석 모델에서의 입력값과 출력값 간의 관계를 학습하여 네트워크를 형성하고, 형성된 네트워크 기반 계측 시의 고유진동수 및 모드형상을 도출하기 위한 Optimized Calibration Parameter를 예측하였다. 인공신경망을 통해 얻은 Optimized Calibration Parameter를 해석 모델에 재차 반영하여 해당 변수 지표에 대한 유효성을 검증한다. 이러한 과정을 통해 Test Bed 현장 계측으로부터 추출한 동특성과 유사한, 즉 실제 대상 건축물의 동적 거동이 유사한 Analytical Model을 생성한다.
Calibration 최적 해 탐색을 위한 인공신경망의 입력값의 개수는 1차 ~ 6차 모드까지의 고유진동수(6개), 그리고 측정 기준층과 측정 방향에 따른 1차 ~ 6차 모드까지의 정규화된 모드형상(84개), 총 90개의 고유진동수 및 모드형상 정보가 입력값으로 사용되었다. 출력값의 개수는 강성, 질량, 구속조건 그룹에 해당하는 총 21개의 Calibration Parameter Index가 사용되었다. 인공신경망 학습에 사용된 데이터의 개수는 초기 설계 모델을 포함하여 총 406개이다. 총 406개의 데이터 중, 365개(약 90%)의 데이터가 훈련에 사용되었고, 41개(약 10%)의 데이터가 검증에 사용되었다.
인공신경망을 통해 Calibration Parameter Index를 예측한 결과, 기둥(C50, C45, C40, C35, C30)은 1.53, 1.52, 1.52, 1.52, 1.52, 유효보(C35, C30)는 1.45, 1.45, 코어 벽체(C50, C45, C40, C35, C30)는 1.61, 1.61, 1.61, 1.61, 1.61, 벨트월(C35) 및 메가보(C30)는 1.49, 인방보(C50, C45, C40, C35, C30)는 1.55, 1.55, 1.55, 1.55, 1.55, 활하중의 질량 고려율은 1.0, 구속조건(지상 저층부, 지하층)은 1.0, 1.0로 산출되었다.
예측된 Calibration Parameter Index 값을 해석 모델에 입력하여 모드 해석을 수행하였으며, 이를 현장 계측 결과와 비교하였을 때, 관심 주파수 대역 내 최소 0.2% ~ 최대 2.6%의 차이가 발생하였다. 이는 본 연구에서 목표하는 Calibration 허용 오차인 10%를 충분히 만족함을 확인하였다.
MAC 값 비교 결과, 병진 방향에 대한 1차 모드, 2차 모드, 4차 모드, 그리고 5차 모드에서의 MAC 값이 최소 0.94 ~ 최대 0.98이며, 비틀림 방향에 대한 3차 모드 및 6차 모드에서의 MAC 값은 약 0.79로, 해석 모델의 모드형상 또한 계측 결과와 비교적 유사한 수준임을 확인하였다.
대상 건축물의 현장 계측 결과와 초기 해석 모델을 비교해보았을 때, 계측 결과와 해석 모델 간의 모드형상은 비교적 유사한 수준이었으나 고유진동수의 차이가 상대적으로 크게 발생하였다. 이에 본 연구에서는 계측 결과와 초기 해석 모델 간 차이가 상대적으로 큰 고유진동수의 Correlation을 주요한 목표로 설정하였고, 초기 해석 모델의 고유진동수를 전역적으로 증가시키기 위해 고유진동수에 대한 민감도가 높은 강성 그룹(주요 구조 부재)의 Index 값을 변경함으로써 Analytical Model Calibration을 수행하였다. 이러한 과정으로부터 생성된 Calibrated Analytical Model은 초기 해석 모델과 비교하였을 때, 모드형상은 전반적으로 유지 및 개선하는 수준에서 고유진동수가 약 23% 증가하였음을 Table 3을 통해 확인할 수 있다.
본 연구는 초고층 건축물의 신뢰성 있는 Analytical Model 생성을 위한 일련의 Calibration Process를 제안한다. 이에 초고층 주거복합 구조물을 Test Bed로 선정하여 상시 상태에서의 진동 계측을 수행하였고, OMA를 통한 실제 대상 건축물의 고유진동수 및 모드형상을 도출하였다. 한편, 현장 자료로부터 설계된 초기 해석 모델과 현장 계측 결과를 Correlation하기 위해 민감도 분석 기반 Analytical Model Calibration을 수행하였다. 실제 대상 건축물과 유사한 시스템 행렬(강성, 질량)을 가지는 해석 모델의 Calibration Parameter를 탐색하기 위해 인공신경망이 사용되었다. 이로부터 예측한 Optimized Calibration Parameter Index를 해석 모델에 반영하였고, 이를 Test Bed와 비교 및 분석하여 허용오차 범위 내 Analytical Model을 생성하였다. 이러한 과정으로부터 초고층 건축물에 대한 Analytical Model Calibration Process의 유효성을 확인하였지만, 본 연구에서는 현장 상황 및 시공 오차 등을 포함한 현장 조건의 불확실성에 대해 강성, 질량, 그리고 구속조건 외의 다른 조건들을 고려하지 못했기에 추후 연구를 통해 보다 다양한 현장 조건들을 반영한 Calibration Parameter를 설정하고, 이로부터 고유진동수 및 모드형상에 대한 민감도 분석을 수행하고자 한다.
본 연구에서는 일련의 Calibration Process를 통해 신뢰성 있는 해석 모델을 생성하였고, 생성한 해석 모델은 추후 지진하중을 포함한 다양한 동적 하중에 대한 상세 해석으로부터 사용성 및 안전성 평가를 수행하는데 활용될 수 있다. 또한 국내외적으로 초고층 건축물의 상태를 평가하고 손상을 예측하기 위한 구조 건전도 모니터링 연구가 활발히 수행되는 상황에서 이러한 Calibration Process는 신뢰성 있는 해석 모델을 생성하기 위한 기초 연구 자료로 활용될 수 있다.
Table 1
Natural Frequencies of Initial Analytical Model
Table 2
MAC Value of Measurement and Initial Analytical Model
Table 3
Comparison of Initial Analytical Model and Calibrated Analytical Model
References
Brownjohn, JM, Xia, PQ, Hao, H, and Xia, Y (2001) Civil structure condition assessment by FE model updating: Methodology and case studies. Finite Elements in Analysis and Design, Vol. 37, No. 10, pp. 761-775.

Heo, SJ, Woo, SS, Mun, BW, and Mun, DH (2017) Analysis of vibration acceleration monitoring data of wind-induced super-tall building and effectiveness evaluation of system identification methods by using output-only data. Journal of the Wind Engineering Institute of Korea, Vol. 21, No. 1, pp. 37-45.

Jeong, JH, Kim, HJ, and Choi, SY (2013) Comparison of design code damping formulae and measured damping ratios of tall buildings under wind loads. Journal of the Architectural Institute of Korea, Structure & Construction, Vol. 29, No. 4, pp. 11-18.

Kim, JY, Yu, E, Kim, DY, and Kim, SD (2009) Calibration of analytical models to assess wind- induced acceleration responses of tall buildings in serviceability level. Engineering Structures, Vol. 31, No. 9, pp. 2086-2096.

Kim, SN, Kim, JH, Song, IH, and Lee, BG (2018) Structural health monitoring of Lotte World Tower. Review of Architecture and Building Science, Vol. 62, No. 11, pp. 35-38.

Moon, KH (2018) Application and case study of structure health monitoring systems for building. Review of Architecture and Building Science, Vol. 62, No. 11, pp. 31-34.

Olsen, P, and Brincker, R (2015). Comparison of mode shape vectors in operational modal analysis dealing with closely spaced modes. Proceedings of the 6th International Operational Modal Analysis Conference (IOMAC 2015). pp. 500-505.

Pastor, M, Binda, M, and Harčarik, T (2012) Modal assurance criterion. Procedia Engineering, Vol. 48, pp. 543-548.

Pierro, E, Mucchi, E, Soria, L, and Vecchio, A (2009) On the vibro-acoustical operational modal analysis of a helicopter cabin. Mechanical Systems and Signal Processing, Vol. 23, No. 4, pp. 1205-1217.

Salawu, OS (1997) Detection of structural damage through changes in frequency: A review. Engineering Structures, Vol. 19, No. 9, pp. 718-723.

- TOOLS