낙석방지울타리의 부재별 에너지 흡수능력에 대한 유한요소해석 연구
A Study on Finite Element Analysis for Energy Absorption Ability of Each Member of Rockfall Protection Fence
Article information
Abstract
국내에서는 낙석붕괴의 위험이 있는 절개사면에 대하여 적절한 낙석방지시설을 설치하도록 하고 있다. 국내의 경우, 낙석방지울타리는 50 kJ의 낙석에너지를 흡수할 수 있도록 설계한다. 낙석방지 울타리의 에너지 흡수 능력에 대한 검증은 주로 실물 낙하 실험을 통하여 이루어진다. 하지만, 실물 낙하 실험은 많은 비용과 노력이 소요되는 단점이 있다. 또한, 실물 낙하 실험에서는 낙석방지 울타리를 구성하고 있는 부재별 에너지 흡수 능력을 측정하기는 매우 어렵다. 실물 낙하 실험의 대안으로 유한요소해석을 사용할 수 있다. 본 연구에서는 낙석방지울타리에 대한 실물낙하실험을 대체할 수 있는 유한요소해석모델을 개발하고 검증하였다. 검증방법으로는 실물낙하 실험결과와 유한요소해석결과를 비교하였다. 이 후 낙석 충돌위치를 변화시키면서 낙석방지울타리의 총운동에너지 소산에 걸리는 시간, 최대 변위 그리고 부재별 에너지 흡수능력을 평가하였다.
Trans Abstract
A rockfall protection facility is usually installed on steep cut slopes to minimize the damage from unexpected falling rocks. In Korea, such rockfall protection fence is designed to have an energy absorption ability of 50 kJ. In order to verify the energy absorption ability of the fence, a real scale drop test can be used. A real scale drop test is the most reliable method to evaluate the energy absorption ability of the fence. However, the real scale drop test is expensive and requires a lot of effort. Moreover, it is hard to evaluate the energy absorption ability of each member of the fence. Alternatively, finite element analysis can be used to evaluate the performance of the fence. In this study, the finite element model is first developed and verified. The finite element analysis results were compared with those from real scale drop test for verification. Then, a series of parametric studies was conducted by varying rockfall locations to evaluate the time it takes for total kinetic energy to dissipate, the maximum displacement, and the contribution of each member of the fence to energy absorption ability.
1. 서 론
낙석방지시설은 도로 절개면의 낙석, 토사 붕괴 등으로 인한 교통장애, 도로구조물의 손상, 재산 및 인명상의 손실을 예방하기 위해 설치하는 구조물이다(MLTM, 2008). 낙석방지시설의 기능은 각 사면에 발생하는 낙석을 예방하거나 발생한 낙석이 도로로 유입되는 것을 막는 것으로 낙석방지시설은 기능에 따라 보강공법(Reinforcement Method)과 보호공법(Protection Method)으로 구분된다. 이 중 보호공법에는 대표적으로 낙석방지망(Rockfall Protection Net), 낙석방지울타리(Rockfall Protection Fence), 낙석방지옹벽(Barrier) 그리고 피암터널(Rock shed)이 있다(MLTM, 2008).
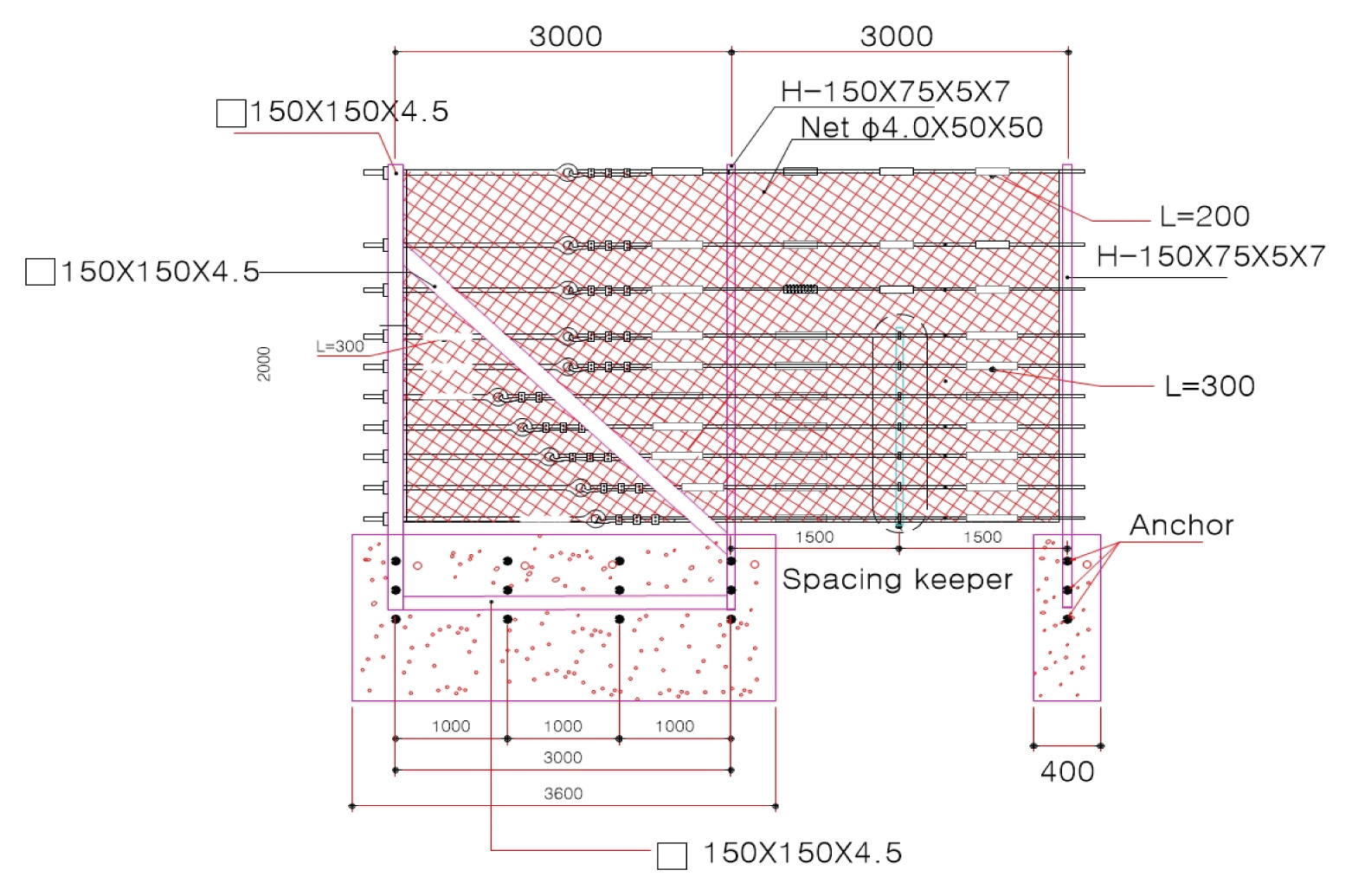
그 중 낙석방지울타리는 낙석방지망과 함께 고속도로 절토사면에 널리 설치되는 시설물이다. 국토교통부에서 작성한 도로안전시설설치 및 관리지침 낙석방지시설 편람(MLTM, 2008)에 따르면 낙석방지울타리는 12.5 m의 높이에서 질량이 400 kg의 낙석이 자유낙하 하는 것으로 상정하여 50 kJ의 충격에너지를 버틸 수 있도록 설계기준에서 제시하고 있다. 국내에서 사용되는 표준 낙석방지울타리의 구성은 Fig. 1과 같이 철망, 와이어로프. 지주, 간격유지대 4가지로 구성된다. 중간지주의 규격은 150×75×5×7 mm 단위규격 이상의 단면계수를 갖는 H형강을 사용하고, 지주의 길이는 2.5 m이상으로 한다. 단부지주의 경우 150×150×4.5 mm 단위 규격의 각형강관이나 H형강을 사용한다(MLTM, 2008).
Fig. 1과 같은 표준 낙석방지울타리에 대한 성능을 검증하기 위한 연구는 여러 연구자들에 의하여 수행되었다. Kim et al. (2015a, 2015b)은 유럽의 낙석방지시설 성능평가 방법인 ETAG 027 (2012)을 기준으로 낙석의 무게를 변수로 하여 수직 실물낙하 실험낙하 실험을 수행하였다. Han et al. (2016)은 낙석방지울타리에 운동에너지를 소산 할 수 있는 추가 부재를 설치하여 낙석방지울타리의 흡수성능을 100 kJ로 증가시키고 ETAG 027 (2012)을 기준으로 수직 실물낙하 시험을 수행하였다. Hwang et al. (2002)은 낙석방지울타리의 구성인 철망과 와이어로프 대신 얇은 철판을 절삭한 부재를 설치한 신형식 낙석방지울타리에 대한 사면 실물낙하 실험을 수행하였다. Koo et al. (2001)은 사면의 기울기와 낙석의 낙하 높이 그리고 낙석의 무게 등의 조건을 변경하여, 사면 실물낙하 실험과 수직 실물낙하 실험을 수행하였다. Seo et al. (2018)은 낙석방지울타리의 지주단면 형상을 변수로 하여 H형강과 각형강관을 사용한 낙석방지울타리에 대한 실물 수직낙하 실험을 수행하였다.
위의 문헌조사 결과와 같이 기존의 연구는 주로 실물낙하 실험을 통하여 성능을 검증하는데 초점이 맞추어져 있다. 일부 낙석방지울타리에 대한 유한요소해석 모델의 개발 및 해석적 성능평가에 대한 연구(Kim et al., 2015a)가 진행되었으나 현재까지는 다양한 조건하에서 낙석방지울타리의 구성요소가 전체 에너지 흡수 능력에 얼마만큼 기여를 하는지에 대한 연구는 미흡한 실정이다. 다양한 조건에서 부재별 에너지 소산 기여도를 평가할 수 있다면, 에너지소산에 기여도 낮은 부재를 파악하여 특정 부재를 보강하거나 부재의 과대 설계를 피할 수 있어 낙석방지울타리에 대한 합리적인 설계가 이루어 질 수 있을 것으로 판단된다.
본 연구에서는 이를 위하여 먼저 낙석방지울타리에 대한 유한요소해석 모델을 실물낙하실험 결과와 비교하여 해석모델을 검증하고 검증된 해석모델을 사용하여 다양한 충돌 위치에 따른 각 부재별 에너지 흡수 능력에 대한 변수해석을 수행하였다.
2. 유한요소 해석모델 정립
2.1 해석모델 개요
본 연구에서는 낙석방지울타리의 실물실험에 대한 유한요소해석을 위하여 범용 유한요소해석프로그램인 ABAQUS (2018)를 사용하였다. 낙석방지울타리의 해석모델은 Fig. 2와 같이 철망, 와이어로프, 단부지주(PEL & PER, Fig. 2), 중간지주(PML & PMR, Fig. 2) 그리고 간격유지대(Spacing keeper)로 구성된다. 위의 모든 부재는 3차원 2절점 보요소(B31)를 사용하여 모델링 하였다. Fig. 3은 본 연구에서 사용된 낙석을 나타내며, 형상은 실물낙하 실험에 일반적으로 사용되는 ETAG 027 (2012)에서 제안하는 형상을 사용하였다. 낙석의 경우, 변형이 되지 않는 강체로 가정을 하였으며 ABAQUS (2018)에서 제공하는 4절점 강체 요소인 R3D4를 사용하였다.
낙석방지울타리의 와이어로프는 단부를 제외하고 지주와 와이어로프의 길이방향(x방향, Fig. 2)에 대하여 구속되어 있지 않다. 따라서, 이러한 거동을 모사하기 위하여 Fig. 2의 A라인의 지주와 와이어로프는 와 방향으로는 동일한 변형을 가지도록 구속을 하고 방향은 자유롭게 이동할 수 있도록 경계조건을 설정하였다. 단부의 경우(B라인, Fig. 2)는 와이어로프가 고정 앵커로 단부에 구속되어 있으므로 와이어로프의 , , 방향 변위 모두를 지주와 같이 움직일 수 있도록 하였다.
철망은 지주와 지주사이의 거리의 1/3지점과 2/3지점(Line C, Fig. 2)에서 서로 구속시켜 해석에서 와이어로프와 분리되지 않도록 하였다. 또한, 간격유지대도 와이어로프와 분리되지 않도록 서로 고정하였다.
유한요소해석에서는 충돌을 모사하기 위하여 Fig. 3의 낙석에 z 방향 초기속도를 작용시켰다. 낙석의 질량이 400 kg이므로 50 kJ의 초기운동에너지를 입력하기 위하여 초기속도는 15.814 m/s로 설정하였다. 또한, 부재 간에 접촉을 모사하기 위하여 ABAQUS (2018)에서 제공하는 General contact 옵션을 사용하였으며, 마찰계수는 이전연구를 참조하여 0.2를 사용하였다(Kim et al., 2015a).
Table 1은 해석에 사용된 재료 물성치를 나타낸다.
철망의 경우, 단면은 원형단면이며, 단면적은 12.56 mm2, 항복강도는 290 MPa이다. 와이어로프도 원형단면이며 단면적은 와이어로프안의 소선의 면적을 사용하였으며 기존 연구를 참조하여 132 mm2로 설정하였다(Kim et al., 2015a). 중간지주, 단부지주, 간격유지대의 형상은 각각 H형, 각형강관, 사각단면이며, 항복강도는 모두 240 MPa로 동일하다고 가정하였다. 모든 부재에 대하여 푸아송비는 0.3으로 가정하였으며 와이어로프를 제외한 부재의 탄성계수는 205,000 MPa로 동일하다. 와이어로프의 경우, 기존 연구를 참고하여 55,400 MPa로 가정하였다(Kim et al., 2015a).
지주의 하단은 이동 및 회전이 모두 구속된 고정지점으로 가정하였으며, 와이어로프의 양 끝단은 해석의 수렴도를 보장하기 위하여 회전에 대하여 모두 구속되어 있다고 가정하였다. 충돌해석의 경우, 접촉을 포함한 여러가지 비선형 문제가 포함되어 있으므로 본 연구에서는 ABAQUS (2018)에서 제공하는 Explicit solver를 사용하여 동적해석을 수행하였다.
2.2 해석결과 및 검증
앞서 소개한 유한요소 해석모델의 검증을 위하여 실물낙하 실험을 모사하여 결과를 서로 비교하였다. 실물낙하 실험에서는 3경간의 낙석방지 울타리에 400 kg의 Fig. 3과 같은 형태의 낙석을 울타리 높이의 1/2지점에 약 15.814 m/s의 속도로 낙하시켜 낙석방지울타리의 성능을 검증하였다. 따라서, 낙석방지울타리에 가해진 충돌 에너지는 50 kJ이다. 실험은 두 가지 경우에 대하여 수행되었다. 첫 번째 실험체는 중간지주와 단부지주 모두 H형 단면(150×75×7×5.5 mm)을 가지며 단부에 사재가 설치되지 않은 경우이며, 두 번째 실험체는 Fig. 2와 같이 단부지주로 각형강관(150×150×4.5 mm)을 사용하고 사재로 보강된 실험체이다. 나머지 철망, 와이어로프, 간격유지대의 제원은 Table 1과 동일하다.
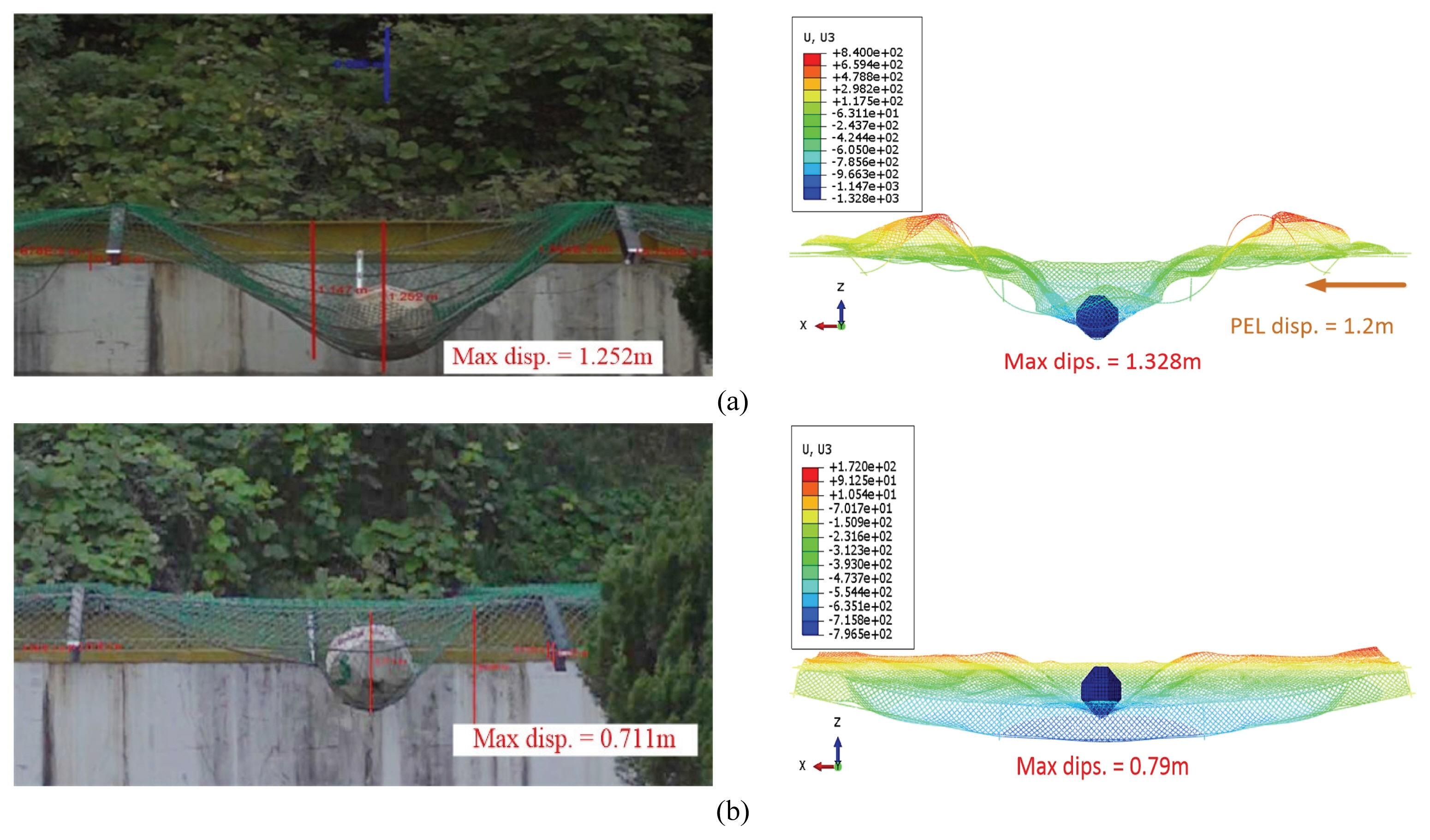
두 실험체에 대하여 유한요소해석을 수행하고 그 결과를 Fig. 4와 같이 비교하였다. Fig. 4(a)와 4(b)는 각각 단부지주 미보강과 보강한 실험체의 결과 나타난 변형 형상을 보여준다. 단부지주 미보강 실험체의 경우, 계측된 최대변위는 1.252 m이었으며 유한요소해석 결과 나타난 최대변위는 1.328 m로 약 6%의 차이를 보였다. 단부 보강 실험체의 경우, 계측된 최대변위는 0.711 m이었으며 유한요소해석 결과로 나타난 최대변위는 0.79 m로 1.1%의 차이가 발생하였다. 실험과 해석결과 나타난 최대 변위는 서로 약 1 ~ 6%의 오차가 발생하였으며, 유한요소해석이 실험결과 나타난 낙석방지울타리의 변형을 잘 모사하고 있는 것으로 판단된다.
또한, 실험에서는 단부 미보강 실험체의 경우, 실험에서 양 끝단 지주(PEL & PER)가 약한 횡방향 강성을 가지며 사재가 미설치 되어있어 중앙(방향)으로 지주 상단이 모아지는 파괴 형상이 발생하였으며 Fig. 4(a)와 같이 유한요소해석에서도 동일한 파괴형상이 관찰되었다. 해석결과, 단부지주 미보강 실험체의 단부상단의 횡방향 변위는 약 1.2 m로 나타났다
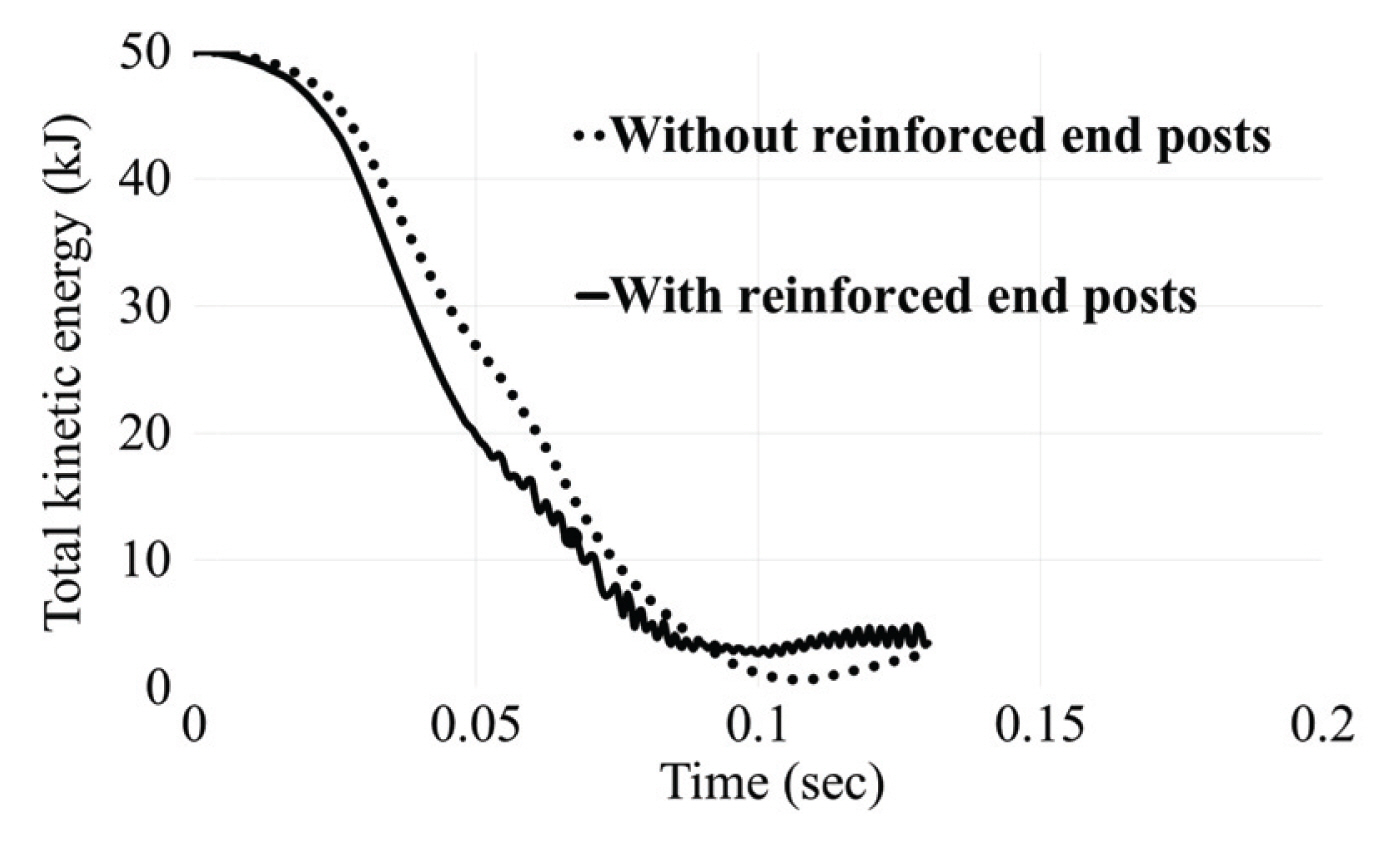
Fig. 5는 해석결과 나타난 해석모델의 운동에너지의 변화를 시간에 따라 나타낸 그림이다. 이 그림에서 알 수 있듯이 단부지주가 보강된 경우, 운동에너지는 보다 빠르게 감소하는 것을 알 수 있다. 단부지주 미보강과 보강된 경우, 운동에너지가 대부분 낙석방지울타리의 변형에 의하여 소산되는 시간은 각각 약 0.1s와 0.15s로 나나났다. 본 연구에서는 부재의 파괴(Fracture)로 인한 요소(element)의 분리는 고려하지 않았으므로 부재의 에너지 소산은 부재의 소성변형과 마찰에 의하여 발생한다.
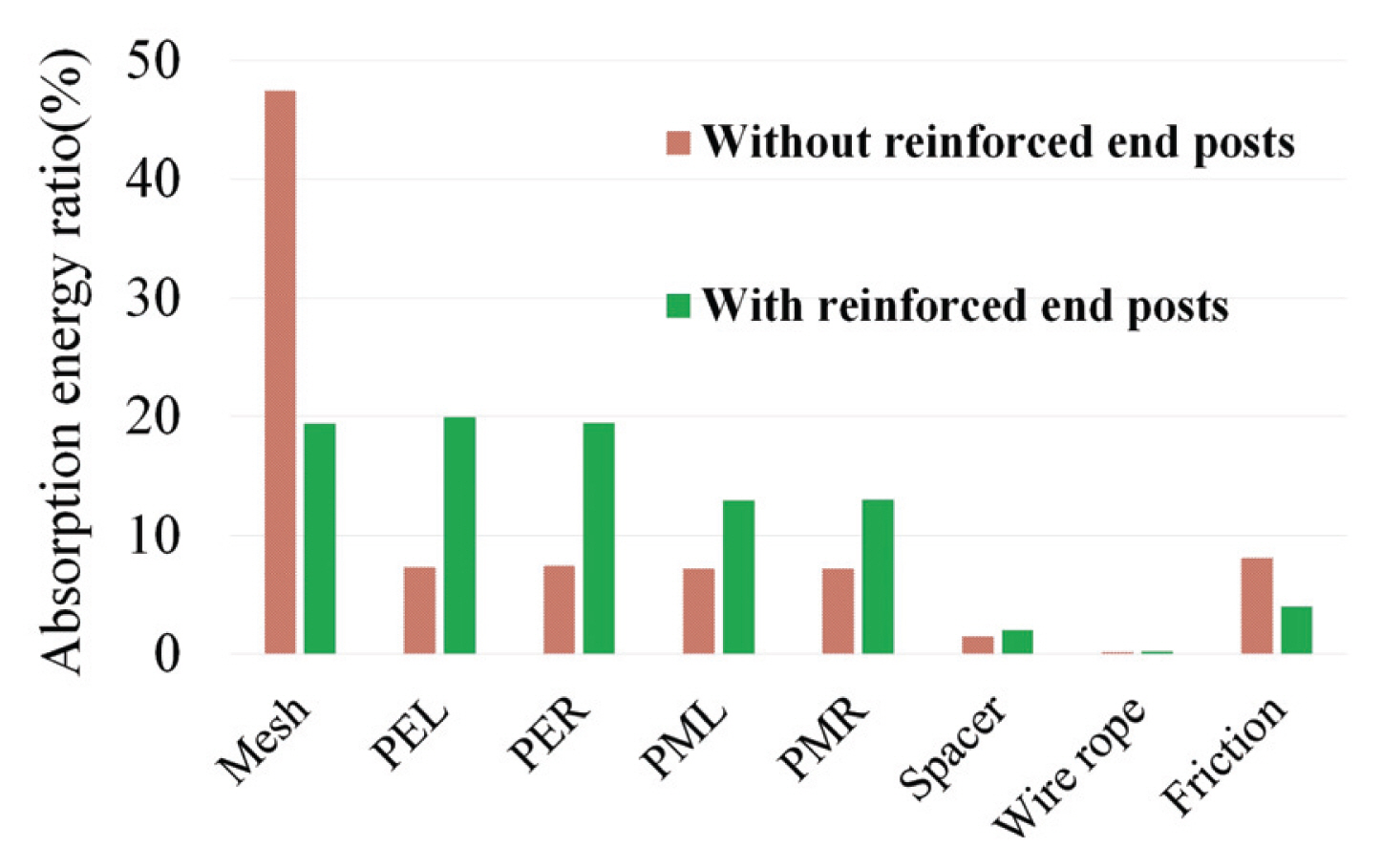
해석시간 동안 발생한 최대변형 발생시간을 기준으로 각 부재의 흡수에너지를 계산하였으며 그 결과는 Table 2와 같다. 또한, 부재별 흡수에너지를 낙석의 초기 충돌 에너지(50 kJ)로 나누어 각 부재별 에너지 소산에 대한 기여도를 표로 나타낼 수 있으며 두 실험체에 대한 결과는 Fig. 6과 같다.
단부 지주가 없는 경우에는 50 kJ의 충격에너지 중 23.7 kJ의 에너지 즉, 약 47%가 철망에서 소산됨을 알 수 있다. 국토교통부 도로안전시설설치관리 지침낙석방지울타리 편람(MLTM, 2008)에 따르면 기존 실험결과를 통하여 낙석방지울타리 설계 시 망의 최대 에너지 흡수능력을 25 kJ로 보고 있어 이 값에 거의 근접하는 것을 알 수 있다. 특히, 단부지주가 보강되지 않은 경우에는 단부지주가 보강된 경우에 비하여 지주의 흡수 능력이 약 36% ~ 56% 정도인 것으로 나타났다. 이는 단부지주 미보강으로 인하여 단부상부가 중앙으로 모아지면서 변형은 크나 에너지 소산에 필요한 항복변형은 상대적으로 작게 발생하기 때문이다. 또한, 두 가지 해석 경우 모두에 대하여 와이어로프의 에너지 흡수능력은 아주 작은 것으로 나타났다. 이러한 이유는 와이어로프의 주된 역할이 낙석에 의한 충격력을 지주에 전달하는 역할을 주로 하며 소성변형은 작기 때문이다.
단부가 보강된 경우는 철망과 단부지주는 약 9.7 kJ ~ 9.97 kJ의 에너지 흡수 능력을 보였으며 중간지주는 약 6.5 kJ의 에너지 흡수 능력을 나타냈다. 이러한 결과로 단부지주 보강을 통하여 에너지 흡수 능력을 고르게 분산 시킬 수 있는 것으로 나타났다.
3. 변수해석
3.1 해석 변수
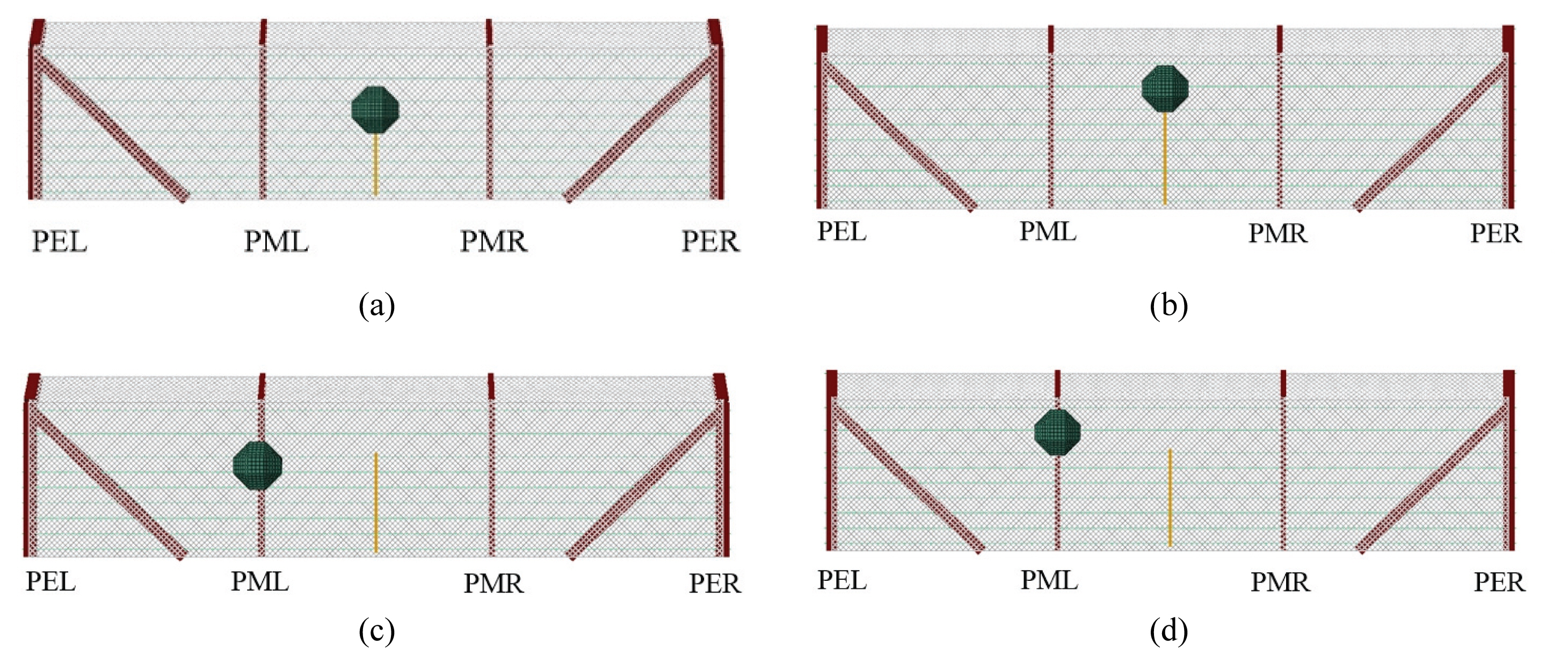
2장에서 검증된 모델을 사용하여 이번 장에서는 변수해석을 수행하였다. 검증 모델 중 단부지주가 보강된 경우가 각 부재별 에너지 흡수능력이 고르게 분포하는 것으로 나타났으므로 단부 보강 모델을 활용하여 변수해석을 수행하였다. 본 연구의 해석 변수는 낙석의 충돌 위치로 Fig. 7과 같다. Fig. 7에서 Case A는 2장의 단부지주 보강 실험체와 동일하며 낙석은 50 kJ의 충돌 에너지를 가지며 충돌 위치는 3경간 낙석방지울타리의 저면으로부터 1/2지점(높이=1.17 m)이다.
Case B는 저면으로부터 2/3지점(높이=1.57 m)에 낙석이 충돌하는 경우로 국내에서 낙석방지 울타리의 설계 시 사용되는 낙석 충돌 위치이다(MLTM, 2008). Case C와 Case D는 각각 높이는 저면으로부터 1/2지점과 2/3지점이며 낙석 충돌은 철망이 아닌 중간 지주에 발생하는 경우이다. 모든 경우에 낙석 충돌 에너지는 50 kJ로 동일하며 충돌 위치에 따른 각 부재별 에너지 소산 능력을 분석하였다.
3.2 변수해석 결과
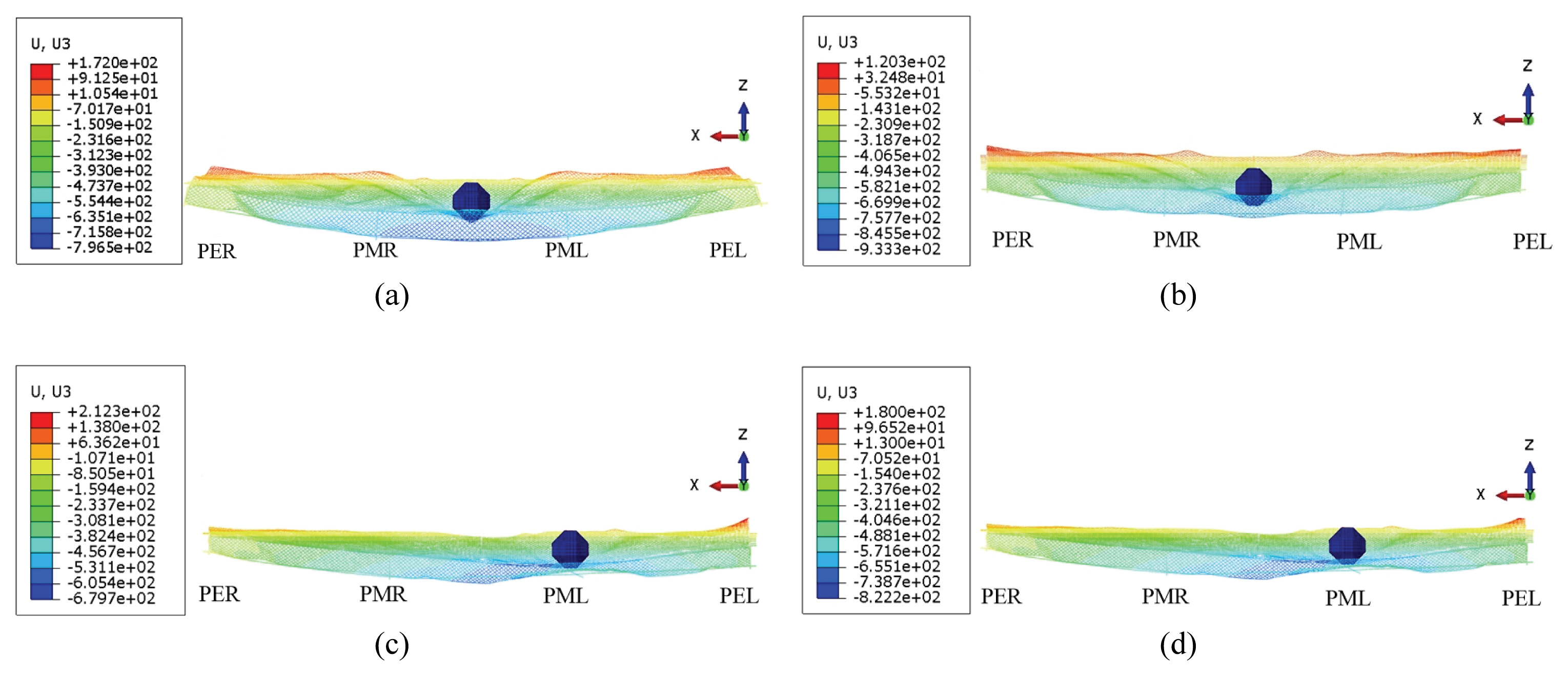
Fig. 8은 각 해석경우에 대하여 z 방향 최대변형 발생 시 변형 형상을 나타낸다. Case A, B, C, D경우에 대하여 최대 변형은 각각 0.72 m, 0.93 m, 0.67 m, 0.82 m 발생하였다. 저면으로부터 2/3지점에 낙석이 충돌하는 경우가 1/2지점에 충돌이 발생하는 경우에 비하여 변형이 약 11% ~ 12% 증가하는 것을 알 수 있었다. 또한, 지주에 낙석이 충돌하는 경우가 철망에 낙성이 충돌하는 경우보다 변형이 약 7% ~ 13% 정도 감소하였다.
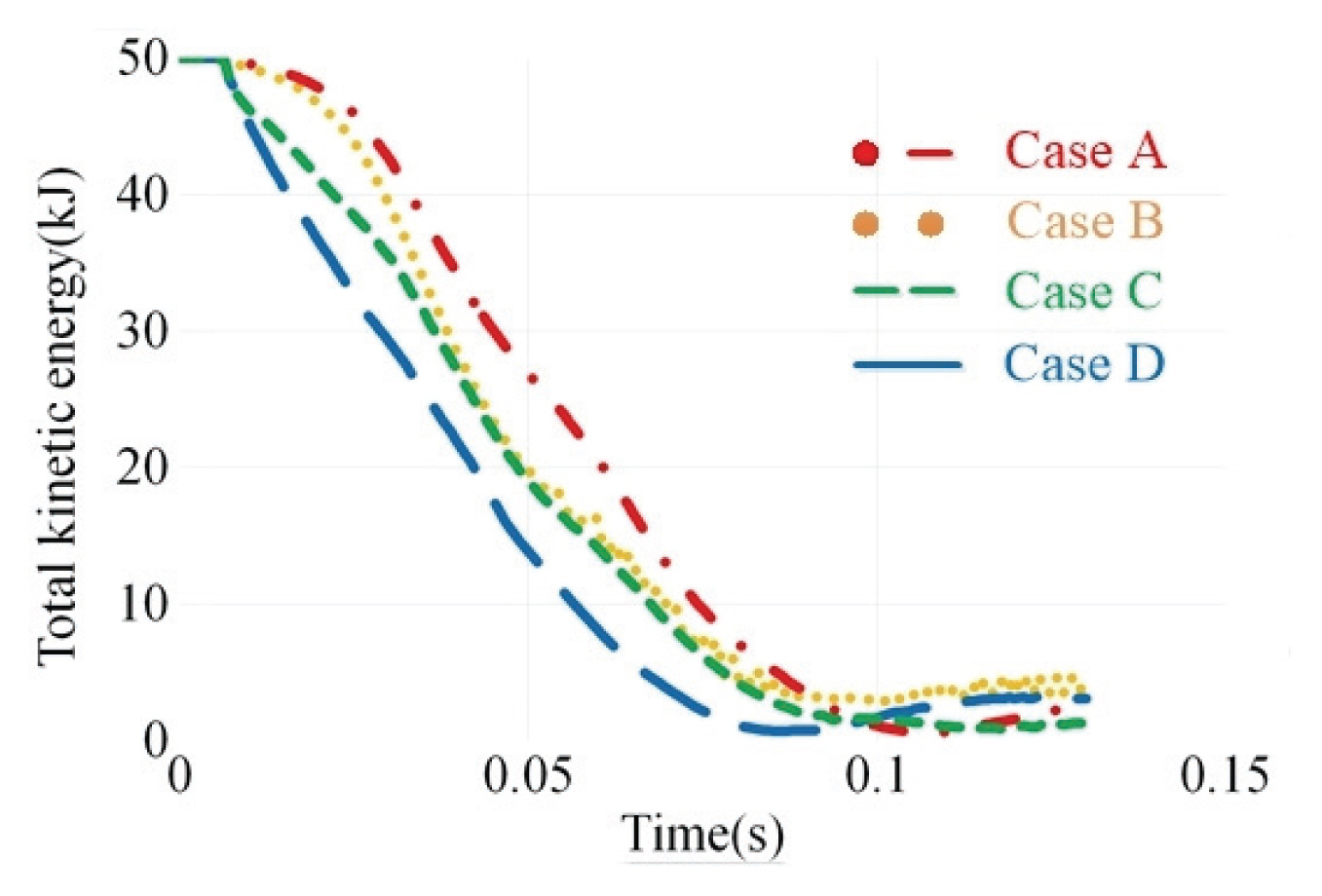
Fig. 9는 해석결과 나타난 Case A ~ D에 대한 총 운동에너지의 시간에 따른 변화를 보여준다. 이 그림에서 알 수 있듯이 저면에서부터 2/3지점에 충돌이 발생하는 경우가 1/2지점에 충격이 가해지는 경우보다 운동에너지가 빨리 감소하는 것을 볼 수 있다. 또한, 철망보다는 지주에 충격이 가해지는 경우에 운동에너지가 빨리 감소하는 것을 알 수 있다. Case A ~ D에서 총 운동에너지는 대부분 0.1s 이후에는 일정한 값으로 수렴하는 것을 알 수 있으며 이 때 대부분의 운동에너지가 부재의 소성변형과 마찰에 의하여 소산되었다.
Fig. 10은 낙석방지 울타리에 최대변형이 발생 한 시점에 각 부재별로 소산한 에너지를 총 충격에너지(50 kJ)로 나누어 백분율로 표시한 그림이다. 이 그림을 통하여 부재별 에너지 소산능력을 비교할 수 있다. Fig. 10에서 알 수 있듯이 낙석이 철망에 충돌하는 Case A와 Case B의 경우, 철망은 19%에서 20%, 중간지주(PML & PMR)는 13%에서 13.9%, 단부지주(PEL & PER)는 17%에서 19%의 충돌에너지를 소산하여 낙석의 충돌 위치에 따른 변화가 크지 않았다. 반면에, 지주에 낙석이 충돌하는 Case C와 Case D의 경우, 각각 철망은 14.7%, 15.5%의 에너지를 흡수하여 서로 유사하나, 충돌 위치의 중간지주의 경우(PML)는 Case C와 Case D에 대하여 각각 42%와 29.7%의 에너지 흡수 능력을 보여 충돌위치에 따른 에너지 소산 정도에 큰 차이를 보였다.
모든 경우에 와이어로프의 에너지 소산 정도에 대한 기여도는 작았으며 50 kJ의 에너지를 대부분 큰 변형 없이 소산하였다(최대 z 방향 변위=0.93 m, Case B, Fig. 8 참조).
변수해석을 종합해 보면 대부분의 충돌에너지는 철망과 지주에 의하여 흡수가 되었으며 2/3지점에 충돌이 발생한 경우가 1/2지점 충돌의 경우보다 더 큰 변형이 발생하였다. 또한, 낙석이 철망에 충돌하는 경우에는 낙석에너지가 각 부재별(철망 및 지주)로 고르게 소산되는 것을 알 수 있었다. 따라서, 극단적으로 지주 자체의 에너지 흡수 능력을 판단할 것이 아니라면 낙석울타리 중앙 경간의 저면으로부터 2/3지점에 낙석을 충돌시켜 낙석방지울타리의 에너지 흡수 능력을 판단하는 것이 바람직한 것으로 판단된다.
마지막으로, 본 연구에서는 단부지주에 고정된 와이어로프에 발생하는 인장력을 해석을 통하여 산출하였다. 그 결과, Case A, B, C, D에 대하여 각각 74.8 kN, 112 kN, 100 kN, 77 kN의 인장력이 발생하였다. 와이어로프의 경우, 그 자체의 에너지 소산 기여도는 작으나 와이어로프는 각 지주에 충격력을 전달하는 역할을 함으로 고정 단부는 계산된 인장력에 충분한 여유를 가지도록 설계를 하여야 할 것으로 판단된다.
4. 결 론
본 연구에서는 낙석방지울타리에 대한 유한요소해석 모델을 실물낙하실험결과와 비교⋅분석하여 정립하고 낙석의 충돌 위치별 낙석방지울타리의 각 구성요소의 충돌에너지 흡수능력에 대하여 연구를 수행하였다. 연구결과 나타난 주요한 결과는 다음과 같다.
(1) 본 연구에서 사용된 유한요소해석 모델과 실물낙하 실험결과 나타난 변형형상은 서로 상당히 유사한 것으로 나타나 해석 모델은 변수해석 모델로서 타당한 것으로 판단된다.
(2) 단부지주가 보강이 되지 않은 경우에는 단부 지주 상단이 안으로 모아지는 파괴 형상이 발생하며 최대 변형 및 철망에 의한 에너지 소산기여도가 증가한다. 따라서, 낙석방지 울타리의 단부지주는 적절히 보강될 필요가 있다.
(3) 단부지주가 보강된 모델에 대하여 변수해석을 수행하였으며, 낙석의 충돌 위치가 지면으로부터 2/3지점의 경우가 1/2지점의 경우보다 최대 변형은 약 11% ~ 12% 증가하였다. 또한, 낙석이 철망에 충돌하는 경우, 낙석 충돌에너지는 철망과 지주에 고르게 분포되는 경향을 보였다.
(4) 모든 해석 경우에 대하여 와이어로프의 에너지소산 능력은 크지 않은 것으로 나타났다. 이는 와이어로프의 주된 역할이 충격력을 지주로 전달하는 것이며 상대적으로 소성 변형은 작게 발생하기 때문이다. 해석결과 단부지주에 연결된 와이어로프에 발생하는 인장력은 최대 112 kN으로 나타났으며 와이어로프의 정착 설계 시 와이어로프에 발생하는 인장력을 적절히 고려하여야 한다.
Acknowledgements
이 논문은 2019년 한국연구재단의 지원을 받아 수행된 연구(NRF-2018R1D1A3B07047459)입니다.