공극 구조의 X-ray microCT 영상화를 이용한 사질토 투수계수 수치적 산정기법
Numerical Computation of Hydraulic Conductivity of Sand Using X-ray Microtomography Imaging of a Pore Structure
Article information
Abstract
다양한 공학 분야에서 다공 매질의 투수계수를 정확하게 예측하는 것은 중요한 사안이다. 최근 X-ray computed tomography (CT) 장비의 발전은 고해상도의 이미지를 해상도 손실 없이 그대로 수치해석에 사용하는 것을 가능하게 했다. 본 연구에서는 X-ray microCT 이미징을 통해 사질토 시료의 공극구조의 고해상도 이미지를 획득한 후, 유한체적법 유체흐름해석에 사용할수 있도록 Python 기반 코드를 이용하여 격자 형식의 메쉬를 생성하였다. 이 메쉬에서 Navier-Stockes 방정식을 CFD코드를 이용하여 수치해석적으로 해석하고, 투수계수를 계산하였다. 수치적으로 계산된 투수계수 결과는 실험결과에 비슷한 값을 보였으며, 26%의 오차를 나타내었다. 유체 벽경계부근에서 높은 해상도의 격자를 구현하지 못하는 한계로 인해, 입력압력조건에 따라 다른 투수계수가 계산됨을 확인하였다. 본 연구에서는 X-ray CT이미징을 통해 수치적으로 다공매질의 투수계수, 투과율 등의 물성을 도출할 수 있다는 가능성을 입증한 연구로써 의의가 있다고 판단된다.
Trans Abstract
Accurate estimation of the permeability of soils plays a major role in many geotechnical engineering practices. Advances in X-ray computed microtomography (X-ray microCT) have facilitated the direct use of high-resolution images for numerical simulation. In this study, a sand column was prepared and its pore-scale images were acquired using X-ray microCT scanning. The resulting images were converted into a finite volume mesh format using Python-based code for computational fluid dynamics. A Navier-Stokes equation was used to solve the flow in the constructed pore structure, and the permeability was computed based on Darcy's law. The computed permeability showed fairly good agreement with the measured value with 26% error. Further improvement in mesh generation technique is necessary because of the insufficient resolution near walls and grain contacts. However, this study suggests the feasibility of using X-ray CT imaging for numerical computation of permeability and the relevant transport properties of porous media.
1. 서 론
지반 물성을 정확하게 예측하는 방법은 핵폐기물 지중처분, 저류암 평가, 이산화탄소 지중저장 등 다양한 지반공학/암반공학에서 쓰이고 있다. 특히 지반공학이나 수리학 분야에서는, 대부분의 지반 물성에 영향을 미치는 투수계수에 대한 연구가 활발하게 진행되고 있다. 투수계수에 영향을 주는 인자로는 유효입경(Hazen, 1892), 공극비 및 비표면적(Kozeny, 1927; Carman, 1956) 등이 알려져 있다. 하지만, 흙 내부의 공극 구조는 무질서하고 불균질하기 때문에 같은 공극비를 가진 구조가 다른 투수계수를 가질 수 있다(Kress et al., 2012). 따라서, 투수계수 평가에서 공극 구조의 형상을 파악하는 것은 매우 중요하다.
공극체의 내부 구조를 확인하는 방법으로서 X-ray computed tomography (CT)가 1967년 발명된 후 활발하게 이용되어왔다. X-ray CT는 한 시료를 회전시키며 여러 각도에서 X-ray를 투사하고 시료 단면에 대한 흡수계수를 사용하여 영상화를 하는 기법이다. 비파괴적으로 공극 구조를 영상화할 수 있다는 장점을 이용하여 최근 다양한 분야에서 활발하게 이용 중이며(Inglis and Pietruszczak, 2003; Iassonov et al., 2009; Chung et al., 2011; Tiwari et al., 2013), 기술의 발달로 μm급 해상도 이상의 이미지를 얻는 것이 가능해짐에 따라 수백 μm 단위의 입경을 가진 입자들을 개별적으로 분석하는 것 또한 가능해졌다. X-ray microCT를 통하여 얻은 이미지를 이용하여 공극비(Perret et al., 1999; Taud et al., 2005; Munkholm et al., 2012; Baek et al., 2019), 거칠기(Fohrer et al., 1999; Kerckhofs et al., 2013), 변형률(Otani et al., 2000, 2002; Alshibli and Hasan, 2008) 등을 확인한 연구들은 많았지만, 투수계수를 구한 연구는 상대적으로 적었다.
이미지를 이용한 투수계수 해석에서 사용 가능한 방법의 하나는 전산 유체 역학과의 연계이다. 지반공학 분야에서는 특히 1956년 개발된 공극 네트워크 모델링(Fatt, 1956)을 이용한 유체의 해석이 이뤄지고 있다. Bryant and Blunt (1992)가 X-ray CT 영상을 이용하여 직접 공극 네트워크를 모델링하는 방법을 개발하였고 일반화 되었으나, 대부분 하드웨어 사양의 한계나 계산시간 단축을 위해 공극 구조를 공극방(Pore chamber)과 공극목(Pore throat)으로 간소화하여 모델링에 사용했다. 그러나, 공극 구조의 형태 또한 공극체의 투수계수에 영향을 줄 수 있으므로 공극 구조를 고해상도로 구현하여 해석에 이용하는 것이 중요하다.
본 연구에서는 투명한 폴리카보네이트 관 안에 사질토 모래 입자들을 다짐하고 X-ray microCT 촬영을 진행하였다. CT 결과 단층 영상은 이진화한 뒤 3차원 영상으로 재구성되었고 3차원 유한 체적 코드의 격자로 만들었다. 변수두 실험을 통하여 사질토 칼럼의 투수계수를 측정하였으며, 같은 압력 조건을 이용하여 수치해석을 진행하고 두 결과를 비교하였다. 분석된 결과를 통하여 개발된 이미지 기반 수치해석방법의 장점 및 한계점 등을 고찰하고자 한다.
2. 재료 및 방법
2.1 재료
조립질 실리카 샌드(Ottawa 20/30, U.S. Silica, Frederick, MD, USA)가 시료로 사용되었으며, Fig. 1에서 볼 수 있듯이 균일한 크기(D50 = 770μm)의 구형 입자들로 이뤄져 있다. 함께 채취된 이물질 등은 실험 전 체가름 시험과 세척을 통하여 제거되었으며, 시편 구축 시에도 균일한 크기 및 종류의 입자들이 사용되었다.
2.2 사질토 시편 설계
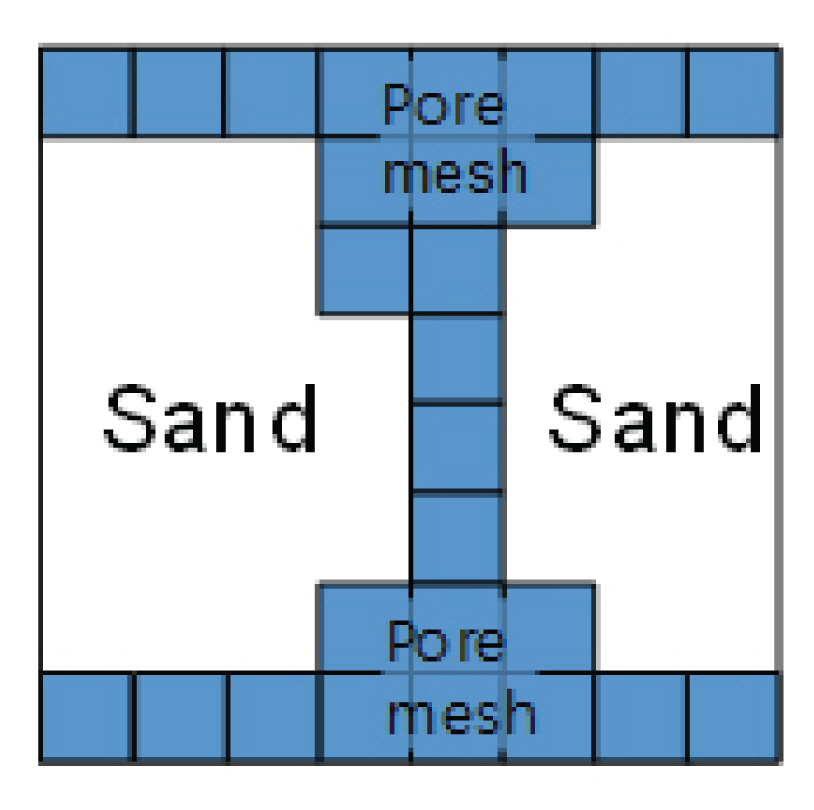
실험에 사용한 사질토 시편은 폴리카보네이트 관, 스테인리스 스프링, 폴리카보네이트 캡으로 구성된다(Fig. 2). 사질토 입자들을 움직이지 않게 고정하면서 유체의 흐름은 자유롭게 하도록 사질토층 상⋅하단부에 500μm의 구멍이 뚫린 폴리카보네이트 캡을 설치하였으며, 스프링을 이용하여 구속조건을 만들었다. 사질토층은 24시간 이상 120도 이상의 오븐에서 건조된 사질토 입자들을 다짐하여 31.9%의 공극비를 가지도록 설계하였다.
2.3 투수계수 측정 실험
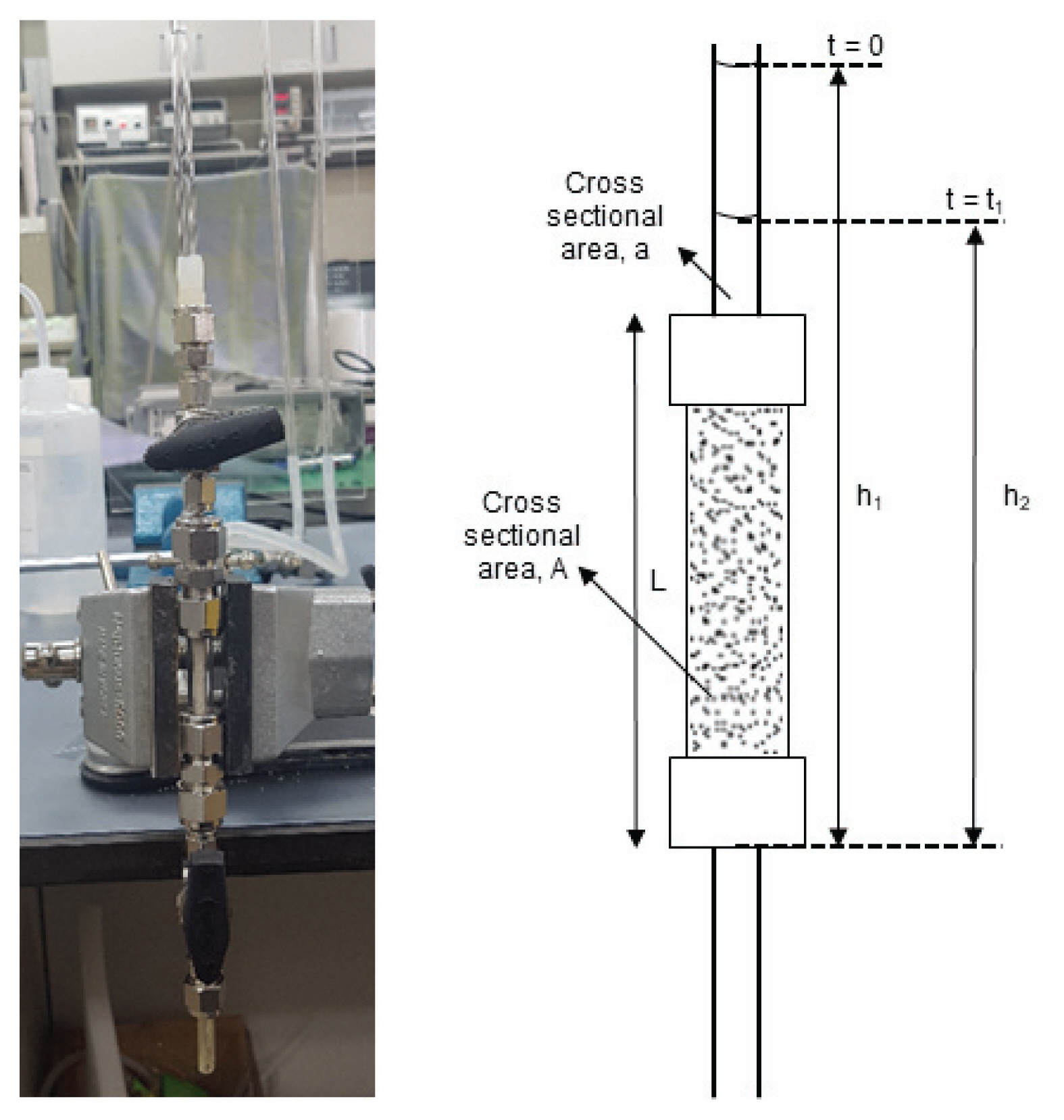
건조 시료를 이용하여 사질토 시편을 구축한 뒤, 변수두 실험(ASTM D5084-16a, 2016)을 통하여 투수계수를 측정하였다(Fig. 3). 공극체 내부에 투수계수에 영향을 줄 수 있는 공기가 차지 않도록 천천히 포화를 시켰으며, 초순수 물을 이용하여 실험하였다. 같은 조건에서 반복성을 검증하기 위하여 5번의 실험을 진행하였고, 가장 근접한 세 값의 평균값을 사용하였다.
2.4 X-ray microCT
투수계수 측정이 완료된 칼럼은 X-선 단층촬영을 위하여 60도의 온도에서 24시간 이상 완전히 건조하였다. 촬영은 건설기술연구원(경기, 대한민국)에서 진행하였으며, 6μm 해상도를 가진 1464장의 단층 이미지를 획득하였다.
2.5 이미지 분석 방법
수치해석용 격자를 만들기 위해서는 이진화 된 단층 이미지가 필요하다. 따라서, 실험적으로 구한 공극비와 이미지의 공극 픽셀 수 계산을 통하여 구한 공극비가 같도록 상 분리를 진행하였다. 임곗값을 설정하여 그 위는 흰색(복셀값 = 1; 사질토), 아래는 검정색(복셀값 = 0; 공극)이 되도록 설정하였으나, 해상도의 한계로 입자 접촉부를 구현하는 것은 오픈소스 소프트웨어인 ImageJ의 MorphoLibJ 플러그인을 이용하였다. 그 결과는 Fig. 4와 같고, 이미지 분석을 통하여 구한 공극비는 32.3%로 실험값과 비교하여 1% 정도의 오차를 보였다.
3. 수치해석 방법
3.1 3차원 격자 생성 및 수치해석 경계조건
X-ray microCT 단층 이미지는 3차원 이미지를 구성하는 최소단위인 복셀로 이뤄져 있으며 각각의 복셀은 정육면체 형태를 띠고 있다. 이진화를 통해서 사질토 복셀에는 1, 공극 복셀에 0을 할당하였고(Fig. 5) 이를 이용하여 격자 생성을 진행하였다. 격자 생성에는 다양한 상용프로그램(Gambit, Gridgen, ICEM, T-grid)이 있으나, 격자 생성이나 수치해석에 사용할 Fluent로 불러오는 시간이 지나치게 많이 드는 단점이 있다. 본 연구에서는 Fluent에서 바로 격자 형태로 불러올 수 있는 텍스트 형태의 파일을 생성하는 코드를 개발하였다. 공극 복셀(복셀값 = 0)의 꼭짓점을 좌푯값으로 변환하는 Python 기반의 코드를 개발하였고, 코드의 결과로 출력되는 텍스트 파일은 Fluent에서 격자 형태로 불러올 수 있도록 하였다. 생성된 격자는 Fig. 6과 같다.
격자를 Fluent로 불러온 후 해석을 위한 경계조건을 설정하였다. 해석에서 wall은 폴리카보네이트 관과 사질토 입자 표면으로 설정하였고, No-slip boundary (wall에서의 속도 = 0)을 부여하였다. Inlet 조건은 pressure inlet, Outlet 조건은 pressure outlet을 부여하였고, 같은 격자를 이용하여 실험조건과 같은 압력 조건 및 다양한 압력 조건에서 수치해석을 수행하였다(Fig. 6). Fluent에서 유체의 흐름은 Navier-Stokes equation에 의해 해석된다. 본 해석에서 유체는 비압축성, 뉴턴 유체로 가정되었고, 층류 유동으로 해석되었으며, 역류는 억제되었다.
3.2 하드웨어 구성
수치해석에 사용된 하드웨어는 두 개의 octa-core Intel Xeon processors (16 threads)과 256GB RAM이 탑재된 워크스테이션이다. 압력 조건에 따라 필요한 메모리 사용량과 해석소요시간의 차이는 있었으나, 최대 메모리 사용량은 210GB였으며, 그때 해석에는 약 6시간이 소요되었다.
4. 결과 및 고찰
4.1 투수계수 실험 및 같은 조건에서의 수치해석 결과
설계한 사질토 시편의 투수계수는 변수두 실험을 통하여 측정하였고, 그 결과 1.23 × 10-9 m2 정도의 일정한 값을 얻었다.
위 수행한 변수두 실험은 모두 같은 수두 차를 이용하여 수행되었으며, 이때의 pressure inlet은 2.34kPa, pressure outlet은 0kPa로 환산된다. 이를 이용하여 수치해석을 진행한 결과, 3.19 × 10-7 m3/s의 질량 유량을 결괏값으로 얻을 수 있었다. 이 결과를 이용하여 투수계수를 계산하기 위해 Darcy’s law를 이용하였다. Darcy’s law는 Eq. (1)과 같다.
Eq. (1)에서 K는 투수계수, Q는 질량 유량, i는 동수경사, A는 유체가 흐르는 매질의 단면적이다. 이를 이용하여 투수계수를 계산한 결과, 1.55 × 10-9 m2로 실험결과와 약 26%의 오차를 보였다.
4.2 수치해석 경계조건에 따른 투수계수 해석 결과 및 고찰
실험과 같은 압력 조건에서의 투수계수 해석결과는 투수계수 측정결과와 큰 차이를 보이지 않음을 확인하였다. 이 투수계수는 공극 구조가 가지는 고유의 물성이다. 또한, 본 연구에서 수행한 해석에서 이용된 이론과 유체의 역류는 억제되는 설정 조건에 따라, 같은 격자로 해석을 진행한 경우 Inlet과 Outlet의 경계조건에 상관없이 같은 투수계수 값을 가져야 한다. 이 이론적 가설을 증명하기 위해서, 실험에 사용된 압력 값에 일정한 배율을 설정하여 pressure inlet을 다양하게 하고, pressure outlet은 0kPa로 고정하여 해석을 진행하였다. 해석에 사용된 값은 Table 1에 나타내었다.
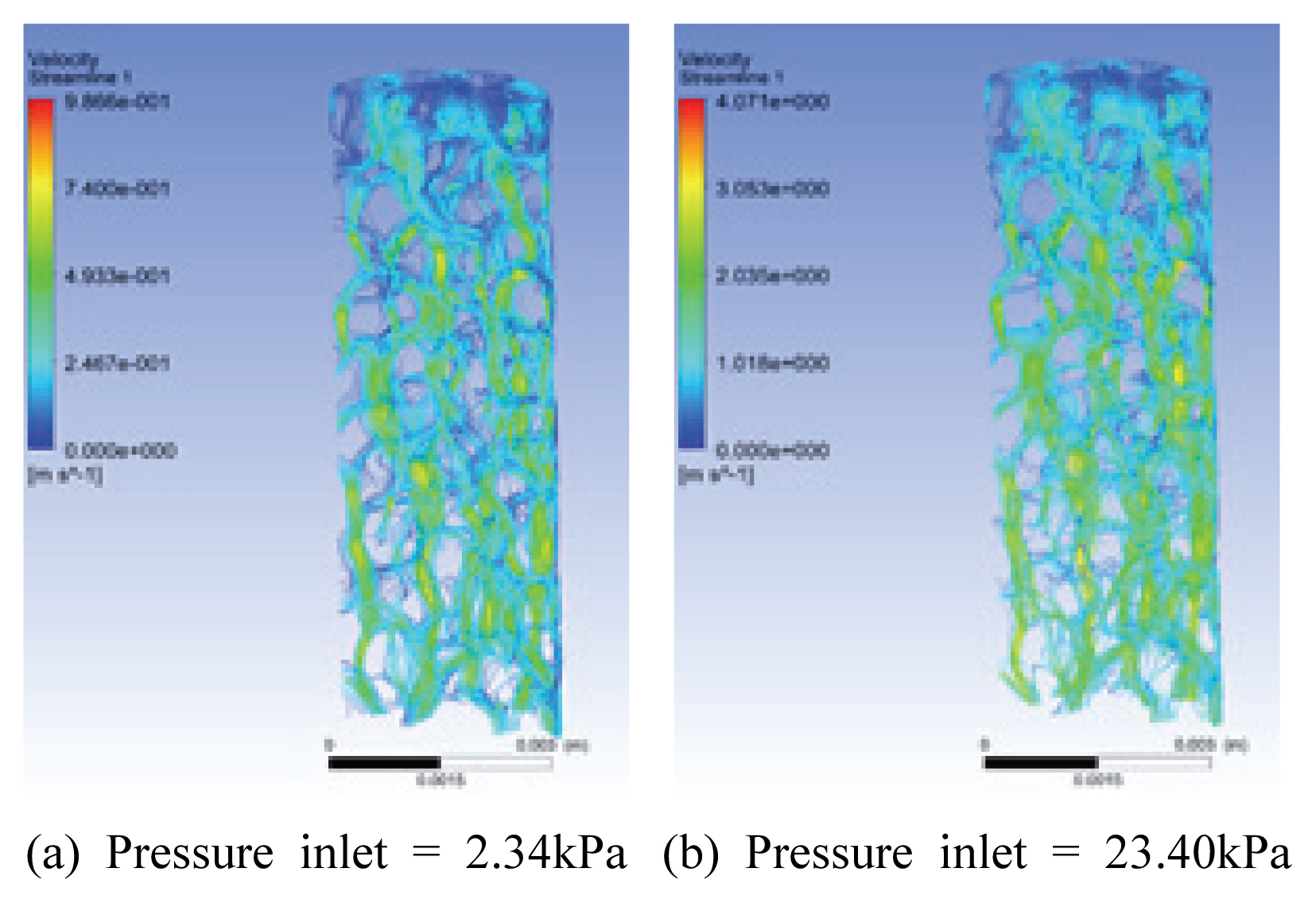
10배율의 pressure inlet을 이용하여 해석하였을 때의 유속 분포 결과는 Fig. 7과 같다. 가장 눈에 띄는 차이점은 pressure inlet에 증가에 따라 특히 좁은 유로에서의 유속이 증가했다는 점이다. 만약 유체의 역류가 억제되지 않았다면, 이 부근에서의 차이가 투수계수 해석결과에 영향이 미쳤을 수 있지만 본 연구에서는 해당하지 않는다.
그러나, 앞서 예상한 결과와는 다르게 pressure inlet 변화에 따른 투수계수 해석결과가 일정하지 않고, 반비례하는 양상을 보였다(Fig. 8). 실험값과 비교하였을 때, 절대 오차범위 26%에서 115%까지의 차이를 보였다.
이런 현상이 나타나는 가장 근본적인 원인은 해석에 이용한 격자에 있다. X-ray microCT 결과로 나온 미가공 이미지를 이진화 이미지로 변환할 때, 가장 먼저 실험을 통해 구한 공극비와 가장 근접한 값을 가지도록 임곗값을 설정하여 진행하였고, 추가로 해상도의 한계로 구현하지 못한 사질토 입자 간의 접촉부를 구현하기 위하여 3D Distance Transform 알고리즘을 이용하였다. 입자 접촉부는 최소 한 복셀(6μm)의 거리를 가진다는 가정하에 공극 복셀이 재생성되었으며 이를 기반으로 수치해석에 필요한 격자가 만들어졌다(Fig. 9).
본 연구에서는 수치해석 경계조건 설정 시 wall을 No-slip boundary로 설정하였기 때문에 wall에 가까운 격자에서의 유속은 0에 가까운 값을 가지게 된다. 따라서 wall 부근에서 정확한 해석을 하기 위해서는 높은 해상도의 격자가 필요하다. 하지만 본 연구에서 개발한 코드는 이를 고려하지 않고, Fig. 9와 같이 공극 구조 전체적으로 같은 크기 및 해상도의 격자를 생성한다. 따라서, wall 부근이나 좁은 유로에서는 정확한 해석이 이뤄지지 않았을 수 있고, 이로 인하여 pressure inlet 설정값에 따라 다른 투수계수 해석결과가 나타난 것으로 확인된다. 따라서 공극 구조 전체적으로 같은 해상도가 아닌, 해석에 사용되는 수식 및 설정에 따라 부분적으로 격자 해상도를 달리하는 방법이 필요하다.
5. 결 론
본 연구에서는 지반공학/암반공학 등 다양한 분야에서 이용될 수 있는 이미지 기반 투수계수 해석 방법을 개발하였다. 기존 이미지 기반 수치해석 방법들은 공극 구조의 형상을 고려하지 않는다는 한계점을 가지고 있다. 따라서 본 연구에서는 이를 극복하기 위하여, μm급 해상도의 이미지를 해상도의 손실 없이 그대로 해석에 필요한 격자 생성에 이용하는 방법을 개발하였다. 변수두 실험을 이용한 투수계수 측정 결과, 1.23 × 10-9 m2의 값을 얻었으며, 실험 조건과 같은 압력 조건을 이용하여 투수계수를 해석했을 때, 1.55 × 10-9 m2 26% 오차를 보이며, 효과적인 이미지 기반 수치해석 방법으로서의 가능성을 보였으나, 이론적 가설을 증명하기 위하여 pressure inlet을 달리하여 해석한 결과에서는 한계점을 보였다. No-slip boundary로 설정된 부근에서의 정확한 해석을 위해서는 부분적으로 고해상도의 격자가 필요하지만, 본 연구에서 개발한 방법으로 생성된 격자는 공극 구조 전체적으로 같은 크기 및 해상도를 가진다. 따라서, 더 정확한 해석을 위해서는 부분적으로, 특히 해석에 사용되는 수식 및 설정에 따라 해상도를 달리할 수 있는 격자생성방법의 개발이 필요하다.
Acknowledgements
본 연구는 국토교통부의 스마트시티 혁신인재육성사업으로 지원되었습니다. 또한, 국토교통부/국토교통과학기술 진흥원의 스마트시티 혁신성장동력 프로젝트 지원으로 수행되었습니다(과제번호 19NSPS-B149840-02). 이에 감사 드립니다.