1. 서 론
수공구조물 설계 문제에 있어 첨두유출량의 산정은 매우 중요한 문제이다(Viessman and Lewis, 2003). 현재 유역의 첨두유출량 및 유출 체적을 산정하기 위한 다양한 방법론들이 존재한다(Chow et al., 1988). 그러나 소규모 유역의 경우에는 주로 합리식이 사용된다(Viessman and Lewis 2003; Hayes and Young, 2006). 중규모의 유역이나 미계측 유역의 경우에도 대략적인 첨두유출량을 가늠하고자 할 때에도 합리식이 종종 사용된다(Rakhecha and Clark, 2000).
합리식은 Mulvany (1851)에 의해 최초로 제안되었다. 합리식의 기본 개념은 강우가 동일한 강도로 내리기 시작하여 무한히 지속된다면 유출량이 도달시간까지는 증가하다 이후에는 평형상태가 된다는 것이다. 이때 유역의 모든 지역이 유출에 기여하게 된다. 합리식은 그 정확성에 대한 의견이 다소 분분하기도 하지만, 사용이 간편하다는 이유로 소규모 유역의 첨두유출량 산정을 위해 선호되는 방법들 중 하나이다(McPherson, 1969; Chow et al., 1988; Haan et al., 1994; Viessman and Lewis, 2003; Dhakal et al., 2011; Grimaldi and Petroselli, 2015).
합리식의 적용상 가장 큰 한계는 강우강도가 일정하게 유지되는 경우에 대한 첨두유출량만을 산정할 수 있다는 데 있다. 비균등한(nonuniform) 강우 분포에 적용하기 어려울 뿐만 아니라 유출 체적과 같은 정보도 알 수 없다(Hua et al., 2003). 이러한 이유로 비균등한 분포의 강우에 대한 적용을 위해 강우 첨두를 전후로 유역의 집중시간에 해당하는 만큼의 시간 구간을 정하고 이 구간의 평균 강우강도를 적용하는 방법이 제안되기도 하였다(이하 평균강우강도 방법이라 칭함; Singh and Cruise, 1992; Guo, 2001). 물론 이 시간 구간의 평균 강우강도는 주어진 호우사상에 대해서 최대가 되어야 한다. 이러한 방법은 특히 직사각형 유역을 가정하는 경우에 유효하다. 유출수문곡선 전체를 얻기 위한 방법으로는 Poertner (1974)가 제시한 수정합리식(modified rational method, MRM)을 들 수 있다. 수정합리식은 일종의 단위도로 삼각형 또는 사다리꼴의 유출수문곡선이다. 이를 수정합리단위도(modified rational unit hydrograph, MRUH)라고도 부른다(Smith and Lee, 1984; Guo, 2001; Bennis and Crobeddu, 2007). 수정합리식은 등분포(uniform)가 아닌 비균등한 강우 분포에도 적용될 수 있을 뿐 아니라, 강우의 지속기간에 상관없이 유출 수문곡선 및 유출 체적을 계산하는 데 이용될 수 있다. 합리식의 또한 그 적용 한계로 제시되고 있는 수 km2 이상의 유역에 대해서도 적용이 가능하다고 알려져 있다(Dhakal et al., 2011).
공교롭게도 두 방법이 모두 합리식에 근거하고 있으나 유도된 첨두유출량이 다를 수 있다는 문제가 있다. 이러한 문제는 대상 유역의 형태가 직사각형이 아니거나 강우의 변동이 더 클 경우에는 더욱 심해질 수 있다. 본 연구는 이와 같이 합리식을 시간 분포된 강우에 적용하여 첨두유출량을 산정하는 경우에 적용할 수 있는 두 가지 방법론, 즉, 평균강우강도 방법과 수정합리식을 적용하는 방법에 대해 그 차이의 정도 및 원인을 파악하는 것을 목적으로 한다. 본 연구에서는 추가로 수정합리식을 적용하여 첨두유출량을 유도할 수 있도록 새로운 적용 방법도 제시하였다.
2. 배경 이론
2.1 합리식
합리식은 Mulvany (1851)에 의해 최초로 제안된 개념이다. 비록 합리식의 정확성에 대한 이견이 있지만, 적용하기가 간편하여 오늘날에도 소규모 유역의 배제시설물 설계 시 가장 널리 사용된다(McPherson, 1969; Chow et al., 1988; Haan et al., 1994; Viessman and Lewis, 2003; Dhakal et al., 2011; Grimaldi and Petroselli, 2015). 합리식의 대표적인 특성은 강우 시간분포와 저류효과(storage effect)를 고려하지 않는다는 점을 들 수 있다(Guo, 2001). 홍수량 산정 결과는 강우강도식에 의존적이며, 강우강도식은 재현기간과 지속기간의 함수로 표현된다. 합리식의 경우 지속기간은 통상 유역의 도달시간으로 가정된다. 따라서, 특정 재현기간의 설계홍수량은 실제 유역의 도달시간에 의해 좌우된다. 이로 인해, 저류 효과를 고려하지 않는 합리식은 유역이 커질 경우 정확성이 떨어진다고 알려져 있다(Biswas, 1971; TxDOT, 2002). 여타 침투손실 모형 대신 유출계수를 사용하여 강우에 직접 적용한다는 점도 합리식의 주요 특성 중 하나이다.
합리식의 기본 개념은 다음과 같다. 만일 강도 I인 강우가 순간적으로 내리기 시작하여 무한히 지속된다면 유출량은 도달시간까지는 계속해서 증가하며, 도달시간 이후에는 유역의 모든 지역이 유역출구 유출에 기여한다. 도달시간 이후에는 강우강도 I와 유역면적 A를 곱한 IA 만큼 일정하게 유입되는 평형상태가 되며, 자연상태의 유역출구에서 발생하는 첨두유출량 Q는 침투 등의 손실량이 있기 때문에 IA 보다 작은 값이 된다. 이와 같은 IA와 Q의 비율을 유출계수 C라 하며 합리식에 의한 첨두유출량(Qp in m3/s in SI units or ft3/s in English units)은 Eq. (1)과 같이 나타낼 수 있다.
여기서, C는 유출계수(0 ≤ C ≤ 1)이다. I는 특정 지속기간에 대한 평균 강우강도(in mm/hr or in./hr)이다. 지속기간은 통상 집중시간으로 가정된다. A는 유역면적(in km2 or acres)이며, mo는 단위 환산계수로 영국식 단위제(English unit)에서는 1, 국제표준단위제(SI unit)에서는 0.2778이다(Hayes and Young, 2006).
2.2 수정합리식
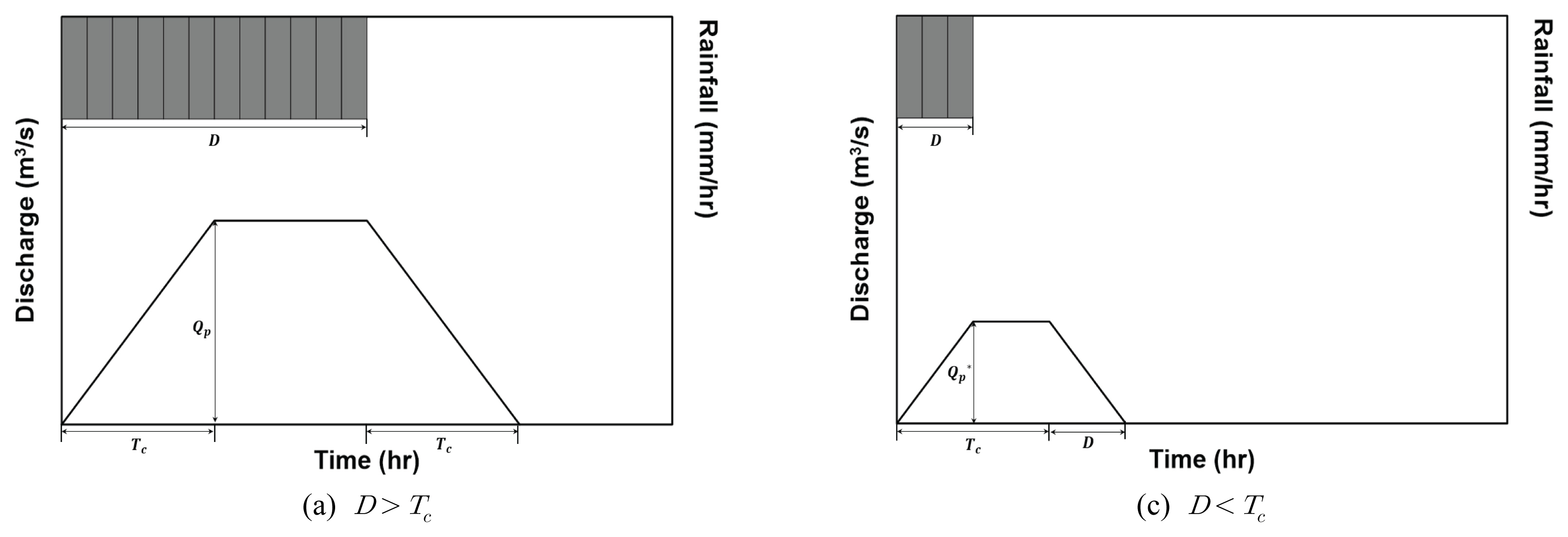
수정합리식이라고 불리는 간단한 삼각형 및 사다리꼴 유출 수문곡선의 유도과정은 다음과 같다. 먼저, 강우의 지속기간이 유역의 집중시간보다 긴 경우에는(D>Tc), 첨두유출량(CIA)이 집중시간(Tc)만큼의 시간이 흐른 뒤에 만들어 진다. 이러한 경우 Fig. 1(a)처럼 유출수문곡선은 사다리꼴의 형태를 가지게 된다. 만일 강우의 지속기간과 유역의 집중시간이 같다면(D = Tc), 유출수문곡선의 형태는 삼각형이 된다. 마지막으로 강우의 지속기간이 유역의 집중시간보다 짧은 경우에는(D < Tc), Fig. 1(b)처럼 유출수문곡선이 사다리꼴의 형태를 가지게 된다. 그러나 이때의 첨두유출량은 CIA (D/Tc)로 작게 산정된다(Smith and Lee, 1984; Walesh, 1989). 이를 정리하면, 먼저, 첨두유출량 Qp는 강우의 지속기간과 집중시간의 대소 조건에 따라 다음과 같이 변하게 된다.
첨두유출량을 전후로 선형적 증가와 감소가 일어나므로(Chien and Saigal, 1974; Singh and Cruise, 1992). 시간에 따른 유량을 첨두유출량과 시간의 항으로 표현할 수 있다. 이를 위해 먼저, 강우의 지속기간이 유역의 집중시간보다 긴 경우(D>Tc), 시간에 따른 유량의 변화 Q(t) 는 Eq. (3)과 같이 표현된다.
한편, 강우의 지속기간이 유역의 집중시간보다 짧은 경우에는(D < Tc), Q(t) 또한 Eq. (4)와 같이 표현할 수 있다.
참고로, 두 번째 경우(D < Tc)의 첨두유출량은 첫 번째 경우의 그것에 D/Tc를 곱한 것과 같으므로, 두 경우의 상승부와 하강부의 기울기, 즉 dQ (t)/dt는 서로 같다는 것을 확인할 수 있다.
2.3 강우 시간분포를 고려한 수정합리식의 첨두유출량 및 첨두시간 산정
2.3.1 강우 시간분포
강우의 시간분포를 위해 고려할 수 있는 모형은 다양하다. 대표적으로 Yen & Chow 모형(Yen and Chow, 1980), Mononobe 모형(Mononobe, 1933), 교호블록(alternating block) 모형(Chow et al., 1988), Huff 4분위 모형(Huff, 1967) 등을 들 수 있다. 먼저, Yen & Chow 모형은 설계 강우의 시간분포를 위해 개발한 방법으로 삼각형 형태의 모형이다. Mononobe 모형 또한 Yen & Chow 모형과 유사하나, 누가강우량을 일련의 식을 통해 축차적으로 산정하여 총 강우량을 분포시킨다. 교호블록 모형은 IDF 곡선 또는 강우강도식을 이용하여 중앙에 최대 강우강도를 위치시키고 좌우로 번갈아 배치시키는 방법이다. 마지막으로 Huff 4분위법의 경우 누가우량곡선을 관찰하여 총 강우지속기간을 4개의 등시간 구간으로 나누고 가장 큰 강우량이 발생하는 부분에 따라 4개의 분위로 구분하여 유도된 무차원 시간별 누가강우량을 이용하여 강우를 분포시키는 방법이다. Mononobe 모형, 교호블록 모형의 경우 첨두 강우는 중앙에 위치하나, Yen & Chow 모형 및 Huff 4분위법은 연구자의 선택에 따라 첨두의 위치가 달라질 수 있다.
본 연구에서는 수정합리식을 이용한 첨두시간 및 첨두유출량 산정을 위한 선제적 시도로, 대칭형의 강우 시간분포를 고려하고자 한다. 앞서 언급된 모형들 중 Yen & Chow 모형에 호우전진계수 0.5를 적용한 경우가 이에 해당한다. 물론, 시간분포를 위해 적용되는 모형에 따라 첨두시간 및 첨두유출량은 달라질 것이다.
2.3.2 수정합리식을 적용한 첨두시간 및 첨두유출량 산정
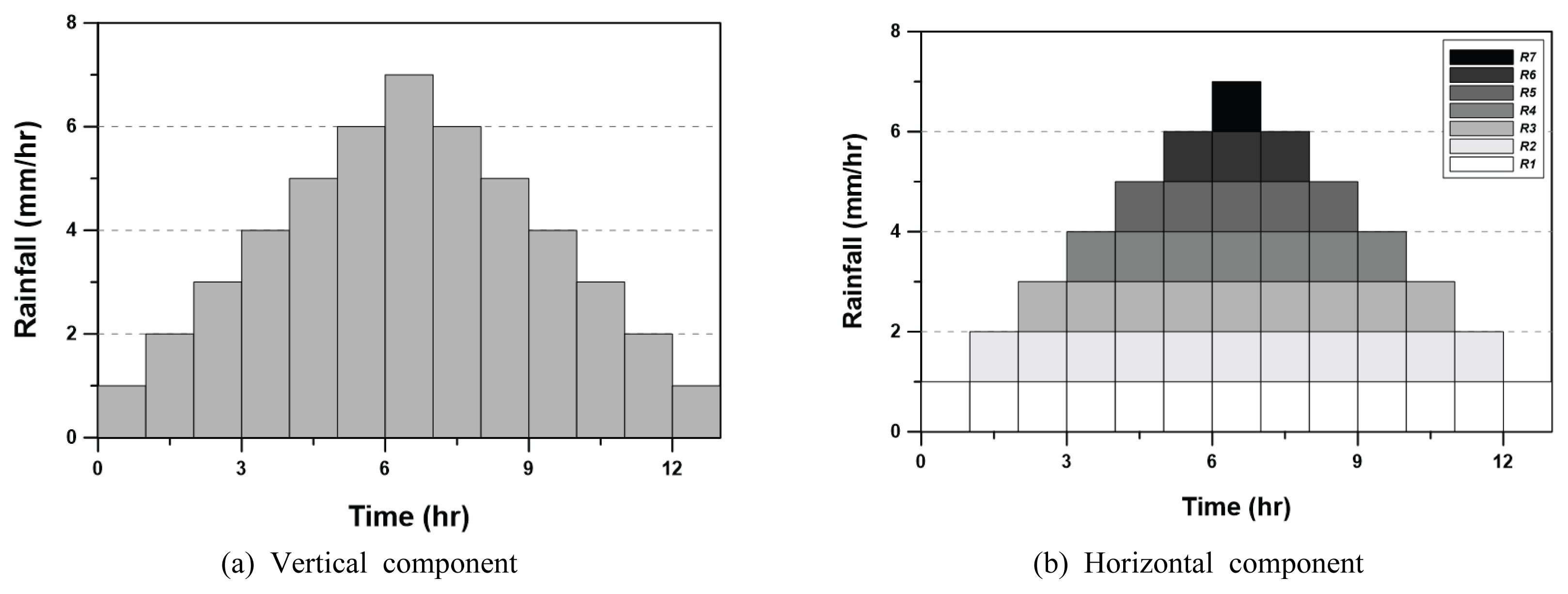
먼저, 다음 Fig. 2(a)와 같은 강우 시간분포를 고려하자. 이 강우 시간분포의 경우 지속기간이 13 hr이며, 매 시간마다 1 mm/hr씩 강우강도가 변하는 형태이다. 이 그림에서 강우강도의 변화는 수직성분으로 표현되어 있다. 이 강우 시간분포는 Fig. 2(b)와 같이 수평성분으로 구분하여 나타낼 수 있다. 이렇게 나타내는 이유는 수정합리식을 적용하기 위함이다. Fig. 2(b)에서 각 수평성분의 높이, 즉, 강우강도를 각각 R1, R2, ..., Rn이라고 하자. 이 그림에서는 각 수평성분의 높이가 동일하게 1이지만 일반적으로 나타내기 위해 기호를 도입하였다.
본 연구에서는 유역의 유출계수를 1.0로 가정하여 계산을 간단하게 하였다. 또한 유역의 집중시간을 5 hr으로 가정하여 유역의 유출계수와 강우의 지속시간과의 다양한 관계가 고려될 수 있도록 하였다. 추가로 분석 과정에 도입되는 기호를 설정하면 다음과 같다. 즉, D 는 강우사상의 총 지속기간(hr), Di는 각 수평성분의 지속기간(hr), Tc는 유역의 집중시간(hr), i는 수평성분의 시점(hr), j는 수평성분의 종점(hr), Ts는 첨두유출의 시점(hr), Te는 첨두유출의 종점(hr) 등이다.
Fig. 2(b)의 각 수평성분은 강우의 분포를 나타내므로 수정합리식을 적용하여 간단히 첨두시간 및 첨두유출량을 산정할 수 있다. 먼저, 각 수평성분에 대한 정보를 정리하면 Table 1과 같다.
첫째, 지속기간이 집중시간보다 긴 경우는 수평성분 R1부터 R4까지이다, 이 경우 첨두유출은 강우가 시작된 후 집중시간만큼 지체된 시점부터 시작되며, 강우가 끝나는 시점에서 첨두유출이 종료된다. 즉, i+Tc에서 첨두유출이 시작(Ts)되며, j에서 첨두유출이 종료(Te)된다(Fig. 3(a) 참고). 두 번째는 지속기간이 집중시간과 같은 경우로 수평성분 R5가 여기에 해당한다. 이 경우 첨두유출의 발생 시점은 i +Tc 또는 j로 표현할 수 있다. 아울러, 이때 수평강우의 강우 시점(i)과 집중시간(Tc), 그리고 지속기간(D)은 D-2i = Tc의 관계를 가진다. 이를 i에 관해 정리하면 i = (D-Tc)/2이다. 참고로, 주어진 유역 및 강우사상의 경우 지속기간(D)은 13 hr, Tc는 5 hr이며, 강우 시점(i)은 4 hr이다. 따라서 첨두시간은 9 hr가 된다(Fig. 3(b) 참고). 마지막으로, 지속기간이 집중시간보다 짧은 경우는 R6부터 R7까지이다. 이 경우 첨두유출은 강우시점에 수평강우 성분의 지속기간을 더한 값 또는 강우의 종점에서 시작하여, 강우의 시점에 집중시간을 더한 시점에서 종료된다. 즉, 첨두유출은 i + Di 또는 j에서 시작하여 i +Tc에 종료된다(Fig. 3(c) 참고).
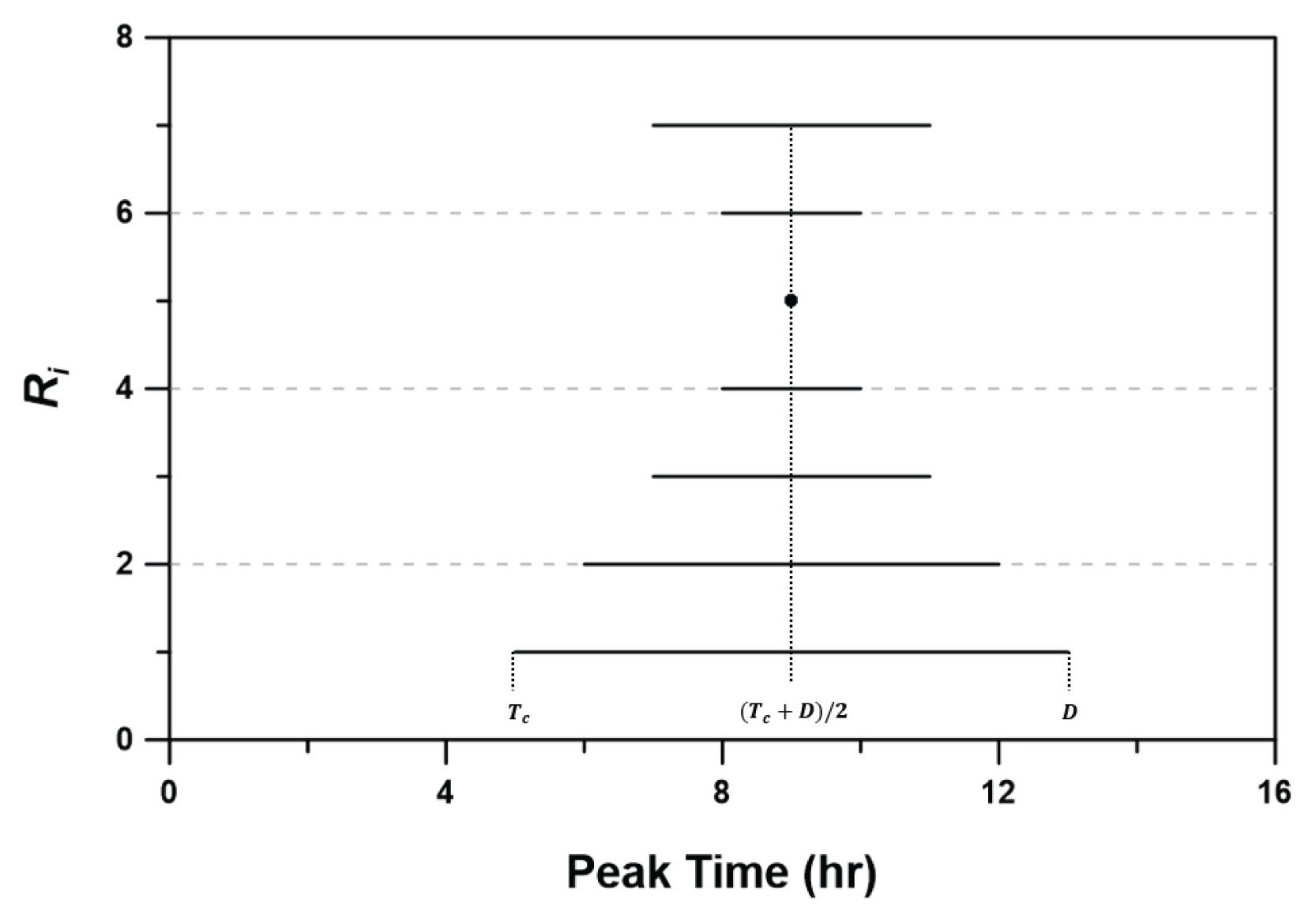
이상의 결과를 종합하여 나타낸 것은 Fig. 4이다. 이 그림을 보면, 전체 강우에 대한 첨두시간은 간단히 (Tc +D)/2로 나타난다. 이러한 결과는 기본적으로 대칭인 강우분포에 대해 유효하다. 그러나 Huff 분포와 같이 왜곡된 분포를 갖는 경우에는 그 정도를 반영하여 다르게 설정될 수 있다. 기본적으로 강우의 첨두를 중심으로 대칭성이 유지되는 최대의 지속기간을 고려하는 것이 필요하다.
결과적으로 이 사례의 경우에는 첨두유출량은 시간 9 hr에서 발생하는 것으로 나타난다. 이러한 결과를 일반화하여 나타내면 Eq. (5)와 같다.
위 식에서, n은 총 수평성분의 수, m은 수평성분의 지속기간이 유역의 집중시간보다 긴 경우의 수, Di는 각 수평성분의 지속기간을 나타낸다.
3. 가상유역 및 강우사상
3.1 가상유역
본 연구에서는 집중시간을 기준으로 1시간부터 24시간까지 총 24개의 가상유역을 고려하였다. 각 가상유역의 면적은 집중시간 산정을 위한 경험식(Kim, 1994)을 이용하여 역산하였다. 사용된 식은 Eq. (6)과 같다.
위 식에서 Tc는 집중시간(hr), A는 유역면적(km2)이다. 이 식을 적용하여 구한 가상유역의 유역면적은 Tc가 1 hr인 경우 2 km2에서 Tc가 24 hr인 경우 8,826 km2까지 다양하다.
3.2 강우사상
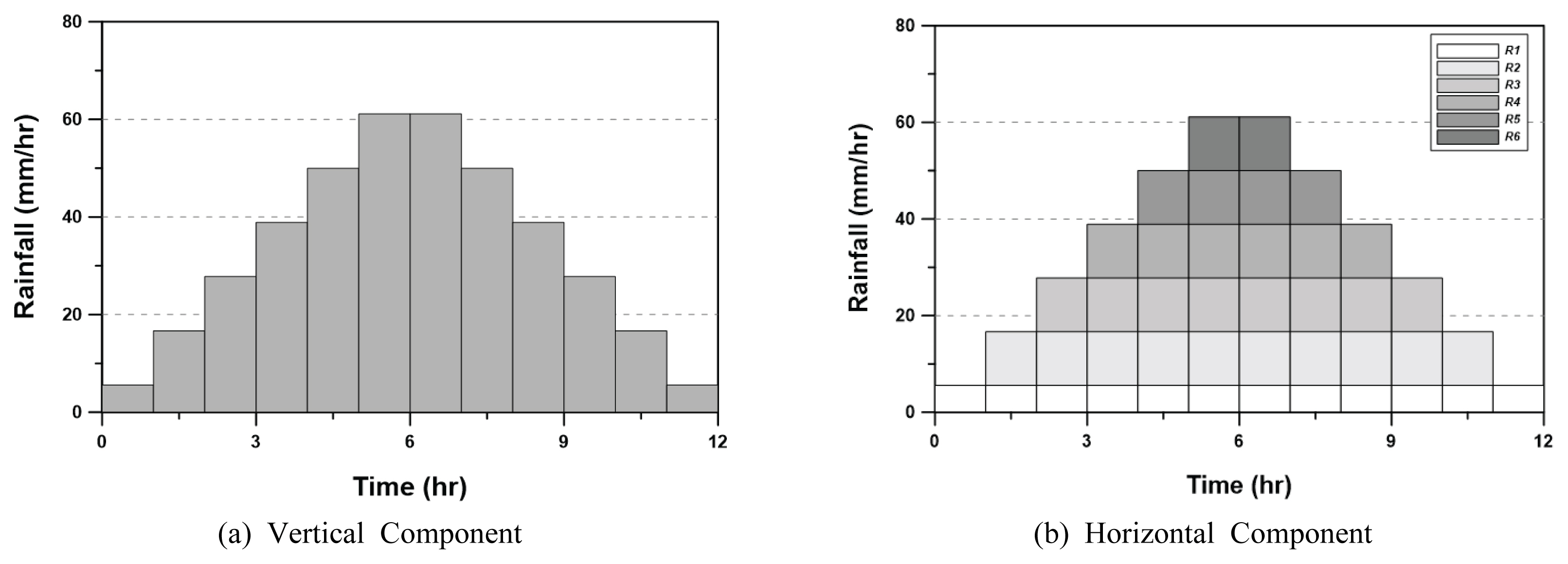
본 연구에서는 12 hr 동안 400 mm의 강우가 내리는 다소 극한 상황을 가정하였다. 아울러 대칭이 되는 시간분포를 위해, 호우전진계수가 0.5인 Yen & Chow 모형을 고려하였다. 해당 분포 또한 역시 중앙부에 첨두부를 가지며, 대칭인 분포이다. 설계강우량이 R (mm)이고 강우지속기간이 D(hr)인 강우사상에 Yen & Chow 모형을 적용하면 면적이 R이고 첨두의 높이 h가 h = 2R/D (mm/hr)인 삼각형 형태의 연속형 우량주상도를 유도할 수 있다. 이 우량주상도는 최종적으로 단위 시간을 가지는 우량주상도로 변환된다. 본 연구의 강우사상을 Yen & Chow 모형으로 시간분포 시킨 결과는 Fig. 5(a)와 같다. 참고로, 지속기간이 홀수가 된다면 단일 첨두를 가지나, 고려되는 지속기간이 짝수이므로 중앙 부분에 두 개의 첨두를 가진다. 평균 강우강도는 33.3 mm/hr, 첨두 강우강도는 61.1 mm/hr이다. Fig. 5(b)에서 지속기간이 긴 수평성분을 R1, 가장 짧은 수평성분을 R6로 표시하였다. 이들 수평성분의 특성은 Table 2와 같다.
4. 시간분포된 강우사상에 대한 수정합리식의 적용
4.1 첨두시간 및 첨두유출량
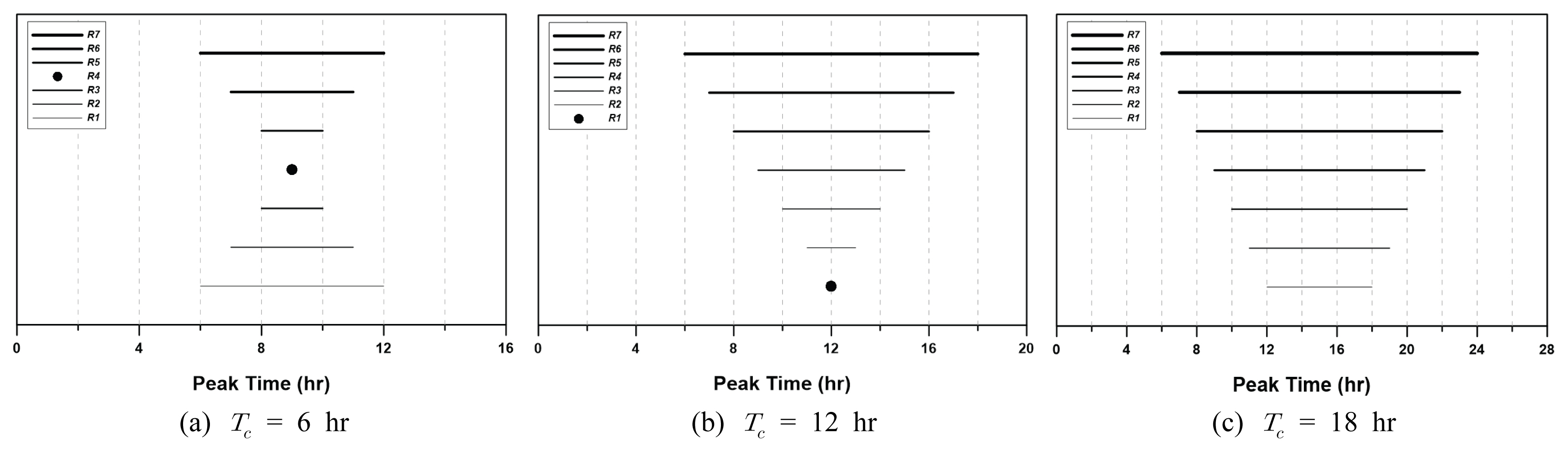
각 유역의 Tc와 D를 알고 있으므로, 앞서 유도한 식인 Tp = (Tc +D)/2를 이용하면 첨두시간을 쉽게 산정할 수 있다. 강우의 집중시간과 지속기간에 따라 총 세 가지 유형, 즉, 강우의 집중시간이 지속기간보다 짧은 경우, 같은 경우, 긴 경우에 해당하는 세 가지 사례를 선정하여 결과를 확인하였다. 고려된 경우(즉, 가상유역)는 #6 (Tc: 6 hr), #12 (Tc: 12 hr), #18 (Tc: 18 hr)이다. 각 가상유역에 대해 산정된 (Tc +D)/2는 9.0, 12.0, 15.0 hr이다. 참고로, 각 가상유역들의 수평강우 성분에 대한 첨두시간 분포는 Fig. 6과 같다. 가상유역 #18의 경우 첨두시간이 12.0-18.0 hr로 나타나나 본 연구에서는 이의 중간인 15.0 hr를 고려하였다.
첨두유출량 산정을 위해서는 먼저 유역의 집중시간(Tc)과 수평강우 지속기간(Di)의 대소 조건을 구분하여야 한다. 먼저, 가상유역 #6 (D>Tc)의 경우, Di ≥ Tc 조건과 Di < Tc조건이 모두 나타난다. 가상유역 #12 (D = Tc)의 경우, 가장 긴 지속기간인 R1만이 Di ≥ Tc 조건을 가지며, 나머지 강우 수평성분은 모두 Di < Tc 조건에 해당한다. 마지막으로 가상유역 #18 (D < Tc)의 경우, 모두 Di < Ti 조건에 해당하게 된다. 앞서 설명한 것과 같이 각 강우 수평성분에 대한 첨두유출량은 Di ≥ Tc 조건의 경우 CIiA, Di < Tc 조건의 경우 CIiA·(Di/Tc) 로 계산된다. 최종적으로, 각 강우 수평성분의 첨두유출량을 합하여 전체 호우사상에 대한 첨두유출량을 산정할 수 있다. 그 결과는 Table 3과 같다. 최종적으로 산정된 첨두유출량은 각 가상유역별로 3,194.7, 13,186.3, 25,557.7 m3/s이 된다.
동일한 방법으로 모든 가상유역의 첨두시간과 첨두유출량을 산정하였다. 그 결과는 Fig. 7과 같다. 대상 호우사상의 지속기간이 12시간이므로 유역의 집중시간이 이 보다 큰 경우에는 첨두유출량이 유역면적이 거의 선형적으로 비례하는 모습을 살펴볼 수 있다.
4.2 합리식의 적용 결과와의 비교
앞서 고려한 유역과 호우사상을 그대로 합리식에 적용하여 첨두유출량을 산정하였다. 물론 유출계수 C도 1.0으로 가정하였다. 그러나 여기서는 합리식의 적용을 위해 등분포된 강우를 고려하였다. 즉, 대상 호우사상은 총 강우량이 400 mm이고, 지속기간이 12 hr, 강우강도가 33.33 mm/hr이다(Fig. 8). 전 장에서의 분석과 동일하게 유역의 집중시간이 12 hr보다 짧은 경우 CI는 33.3 mm/hr로 산정된다. 그러나 유역의 집중시간이 12 hr을 초과하는 경우에는 강우가 유역의 집중시간만큼 지속되지 못하고 중간에 멈추게 된다.
사실 합리식은 강우가 중단 없이 지속되는 경우에 한정된 방법이다. 따라서 강우가 유역의 집중시간보다 짧게 지속되면 합리식의 적용에 문제가 발생하게 된다. 본 연구에서는 이러한 문제를 보완하기 위해 유역의 형상을 직사각형으로 가정하였다. 유역의 형상계수와 관계없이 유역을 직사각형으로 가정할 수 있다면 유역의 집중시간보다 짧은 강우에 대해서도 간단히 합리식을 적용할 수 있다. 즉, 간단히 주어진 강우의 지속기간을 유역의 집중시간으로 늘려주고 반대로 강우강도를 줄여주면 된다. 물론 총 강우량은 동일하게 유지되어야 한다. 예를 들어, 집중시간 24시간인 경우를 가정하면 당초 지속기간 12시간에 해당하는 강우강도 33.3 mm/hr를 절반에 해당하는 16.7 mm/hr로 줄여주면 된다. 이러한 방식으로 합리식을 적용한 결과는 Fig. 9(a)와 같다. 참고로 첨두유출량의 발생시점은 유역의 집중시간이 강우의 지속기간인 12시간보다 짧은 경우에는 유역의 집중시간이 되고, 유역의 집중시간이 강우의 지속기간보다 짧은 경우에는 강우가 끝나는 시점이 된다.
Fig. 9(a)에 나타난 첨두유출량 산정결과를 살펴보면 다음과 같은 특징을 확인할 수 있다. 먼저, D ≥ Tc인 경우, 첨두유출량 산정을 위해 동일한 강우강도(즉, 33.33 mm/hr)가 적용되므로 이 경우 첨두유출량은 정확이 유역면적(A)에 비례하는 형태가 된다. 그러나 D < Tc인 경우에는 유역의 집중시간 증가에 따라 유역면적이 증가하기는 하지만 반대로 고려되는 강우강도가 이에 반비례하여 감소되므로 첨두유출량의 증가는 좀 더 완만한 형태로 바뀌게 된다.
이러한 결과를 수정합리식의 적용 결과와 비교한 것이 Fig. 9(b)이다. 보다 효과적인 시각적 비교를 위해 전대수지에 나타내었다. 두 경우를 비교하는 경우 가장 큰 차이는 강우 지속기간이 유역 집중시간보다 긴 경우 합리식을 적용하여 산정한 첨두유출량이 수정합리식을 적용하여 산정한 첨두유출량보다 더 작다는 점이다. 물론 이러한 결과는 강우의 시간분포에 따른 영향이다. 만일, 수정합리식의 적용이 있어 강우를 시간 분포시키지 않았다면 그 결과는 합리식의 적용 결과와 정확히 일치할 것이다. 결과적으로 합리식의 적용에 있어 강우 시간분포의 영향은 강우의 지속기간이 유역의 집중시간보다 긴 경우에 크게 나타난다. 이 결과는 합리식의 적용에 큰 문제가 있을 수 있다는 것을 의미한다. 합리식 적용의 기본 가정이 강우가 중단 없이 일정한 강도로 지속되어야 한다는 것이기 때문이다. 합리식을 적용하여 추정한 첨두유출량은 시간분포가 고려되는 실제 첨두유출량보다 크게 과소 추정될 수 있다.
이러한 문제는 모의된 또는 관측된 강우사상에 합리식을 적용하여 첨두유출량을 산정하는 경우에도 그대로 나타난다. 강우사상의 지속기간이 긴 경우에도 마찬가지이다. 예를 들어, 강우사상의 지속기간이 유역의 집중시간보다 긴 경우 합리식을 적용하여 첨두유출량을 산정하는 방법은 강우의 첨두 전후로 유역의 집중시간 만큼 가장 큰 강우량을 만들어주는 부분을 선택하고 이때의 평균강우강도를 그대로 합리식에 적용하는 것이다. 그러나 이렇게 만들어진 첨두유출량은 실제 첨두유출량보다 크게 작을 수 있는 것이다. 물론 강우의 시간분포가 반영되지 못했기 때문이다.
유역의 집중시간이 강우의 지속기간보다 긴 경우에는 두 방법의 첨두유출량이 같은 것으로 확인되었다. 물론 이러한 결과는 유역의 형상이 직사각형이라는 가정하에 얻은 것이다. 만일 보다 실제적인 유역의 형태를 반영한다면 그 결과는 달라질 수 있을 것이다. 이상과 같은 결과는 강우의 지속기간을 달리한 적용에서도 동일하게 확인되었다.
5. 결 론
본 연구에서는 시간 분포된 강우사상에 합리식을 적용하는 두 방법, 즉, 유역의 집중시간 만큼에 해당하는 평균 강우강도를 적용하는 방법(평균 강우강도 방법)과 수정합리식을 비교하였다. 대상 유역으로는 유역의 집중시간을 1시간에서 24시간까지로 하여 고려하였으며, 대상 호우사상은 그 첨두가 중앙에 위치한 Yen & Chow 모형을 이용하여 모의하였다. 강우사상의 지속기간을 12시간으로 하여 강우 지속기간과 유역의 집중시간 사이에 다양한 경우가 반영될 수 있도록 하였다. 추가로 본 연구에서는 수정합리식을 적용하여 첨두유출량을 유도할 수 있도록 새로운 방법도 제시하였다. 본 연구의 결과를 요약하면 다음과 같다.
먼저, 본 연구에서는 시간 분포된 강우사상에 수정합리식을 적용할 수 있도록 강우사상을 수평성분으로 분할하여 적용하는 방법을 제시하였다. 이는 기존의 유출해석 방법이 모두 강우사상을 수직성분으로 분할하여 적용하는 것과 정반대의 방법이다. 이 방법을 적용하는 경우 특히 첨두유출량 및 첨두시간을 쉽게 산정할 수 있음이 확인되었다.
두 번째, 시간 분포된 강우사상에 평균 강우강도 방법과 수정합리식을 적용하는 경우의 가장 큰 차이는 강우의 지속기간이 유역의 집중시간보다 긴 경우에 발생함을 확인하였다. 이 때, 합리식(평균 강우강도 방법)을 적용하여 산정한 첨두유출량이 수정합리식의 적용하여 산정한 첨두유출량보다 훨씬 작게 나타났다. 사실 이러한 결과는 합리식 적용의 기본 가정이 강우가 중단 없이 일정한 강도로 지속되어야 한다는 점에서 문제의 소지가 있다. 즉, 시간분포를 고려하지 않는 합리식의 첨두유출량은 과소 추정의 위험성이 크다. 유역이 특히 작은 경우에 이런 문제가 부각될 가능성이 크다.
마지막으로, 이러한 문제가 유역의 집중시간이 강우의 지속기간보다 긴 경우에는 크게 완화된다는 점이다. 유역의 형상을 직사각형으로 가정할 수 있는 경우에는 두 방법의 차이가 없는 것으로 확인되었다. 물론 유역의 형상이 직사각형이 아닌 경우에는 다른 결과가 유도될 수 있다.