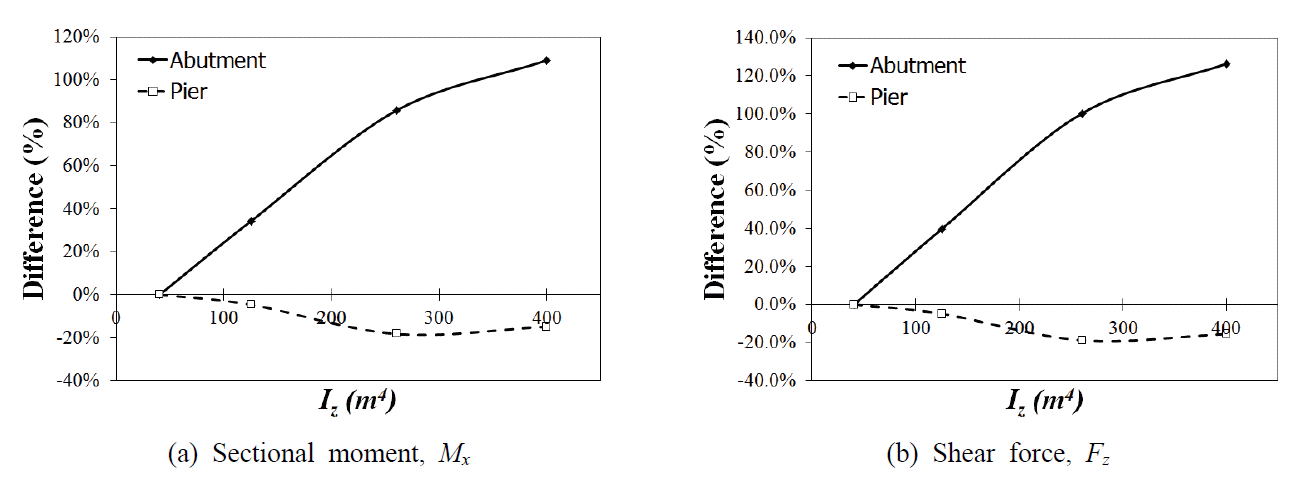|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(2); 2018 > Article |
|
Abstract
Since the fully integral bridge constructed without any expansion joint or bridge bearing integrates the substructure and the superstructure. Thus, feasible horizontal force effects due to earthquake or vehicle braking for example is mainly prevented by the end restraining abutment, and it makes piers and superstructures slimmer and the economics and aesthetics of the bridge system can be greatly improved. This study examines the behavior of fully integral abutment bridges through response spectrum method and parametric studies, and then it assesses the appropriate stiffness of the end-restraining abutments. The horizontal displacements and the sectional member forces like moments and shear force are well restrained in the intermediate piers. It is confirmed that the fully integrated bridge design developed in the study meets the allowable stress requirements suggested by Korean Railroad Design Standards through installing the end restraining abutments with a proper stiffness and prestressed tendon arrangement.
요지
완전일체형 연속교는 상부구조와 하부구조를 일체로 강결시킨 구조형식의 교량으로, 지진하중 등의 수평하중을 강성이 큰 교대가 직접 부담하게 함으로써 교대 외의 모든 부재를 슬림하게 만들어 경관성과 경제성, 내진 성능을 획기적으로 향상시킨 교량형식이다. 이 연구에서는 최대 수평하중(지진하중)을 적용하여, 교대 강성에 따른 구조 해석적 변수해석을 통하여 상부구조, 변위제어 교대 및 중간교각 간 상호작용에 따른 수평하중의 분배특성을 분석하였다. 교대의 강성에 따른 변수해석을 통해 효과적으로 수평변위를 제어하는데 필요한 강성을 파악하였다. 교각이 부담하는 밑면전단력 및 전도모멘트가 크게 감소하므로 교각과 상부구조가 슬림하게 구현될 수 있어 경제성뿐만 아니라 미관 향상에도 효과적일 것으로 보인다. 교대와 상부구조물의연결조건을 시공단계별로 달리하고 변위제어 교대와 강연선을 적절히 배치하여 설계기준이 제시하는 허용응력을 만족하는 것을 확인하였다.
완전일체형 연속교(Integral Continuous Bridge)는 교량 상부구조와 교대, 교각 및 기초 등 교량의 기본 구성요소인 상부구조와 하부구조 전체가 일체로 거동하도록 강결시킨 것을 특징으로 하는 교량형식이다. 교량의 모든 구조 요소를 강결함에 따라 지진하중 등의 수평하중을 강성이 큰 교대가 직접 부담하게 함으로써 교대 외의 모든 하부구조를 슬림하게 만들 수 있고 이로써 경제성과 내진 성능, 미관 등을 향상시킨다. 뿐만 아니라, 완전일체형 연속교량은 교량 받침, 받침점검시설, 신축이음 등 고가의 교량 부속품을 생략할 수 있는데, 이러한 부속품의 잦은 파손에 의한 수리 및 반복 교체로 인해 유발되는 유지관리 생애주기 비용을 최소화할 수 있는 저비용⋅고성능 교량이다. 유지보수도 다른 교량에 비해 편리하여 일상적인 교량점검이 어렵거나 유지보수의 주기가 긴 지역에 유리하다.
이러한 완전일체형 연속교량은 세계적으로 확대 적용 추세에 있다. 일본에서는 교각을 상부구조에 모두 강결시킨 5경간 규모의 라멘형 PSC 박스거더교가 상용화되었고, 독일의 경우 편측 교대를 제외한 구조 부재 전체를 일체화한 총연장 530 m의 세미-일체형교량이 최근 상용화되었다. 하지만 현재까지 국내에서는 철도교의 경우 연속교 사용이 극히 제한적이고, 도로교마저도 받침을 배제한 라멘구조는 거의 사용되지 않는 추세이다. 이러한 실정은 교량 기술의 발전과 건설비의 절감을 어렵게 할 뿐만 아니라, 지속적인 유지관리비를 발생 시킨다. 또한 우리나라 실정에 맞는 일체식 교량 설계시공 사례가 제한적이며, 일체식 교량의 거동특성 및 하중분배 효과의 영향에 대한 연구가 부족한 실정이다. 따라서 본 논문에서는 완전일체형 교량에서 핵심 기능을 담당하는 변위제어 교대의 구조 및 강성에 따른 변수해석적 구조해석을 수행하여 수평하중의 영향에 따른 변위, 모멘트 및 밑면전단력의 분배특성을 분석하고, 변위제어 효과를 정량적으로 평가하고자 한다. 이때 지진하중에 대한 교축방향 및 교축직각방향의 거동을 단일모드 스펙트럼법과 다중모드 스펙트럼법을 사용하여 교대의 적정 강성에 대한 평가를 수행하였다. 이와 같이 정해진 연속교 모형에 대해 시공단계별 해석을 진행하고 시공단계별 응력과 변위를 검토하여 국내 설계기준을 만족하는 설계안을 구성하였다. 이에 따라 교각과 상부구조가 슬림하게 형성될 수 있음을 확인하였고, 이로 인해 경제성과 미관이 향상될 것으로 기대된다.
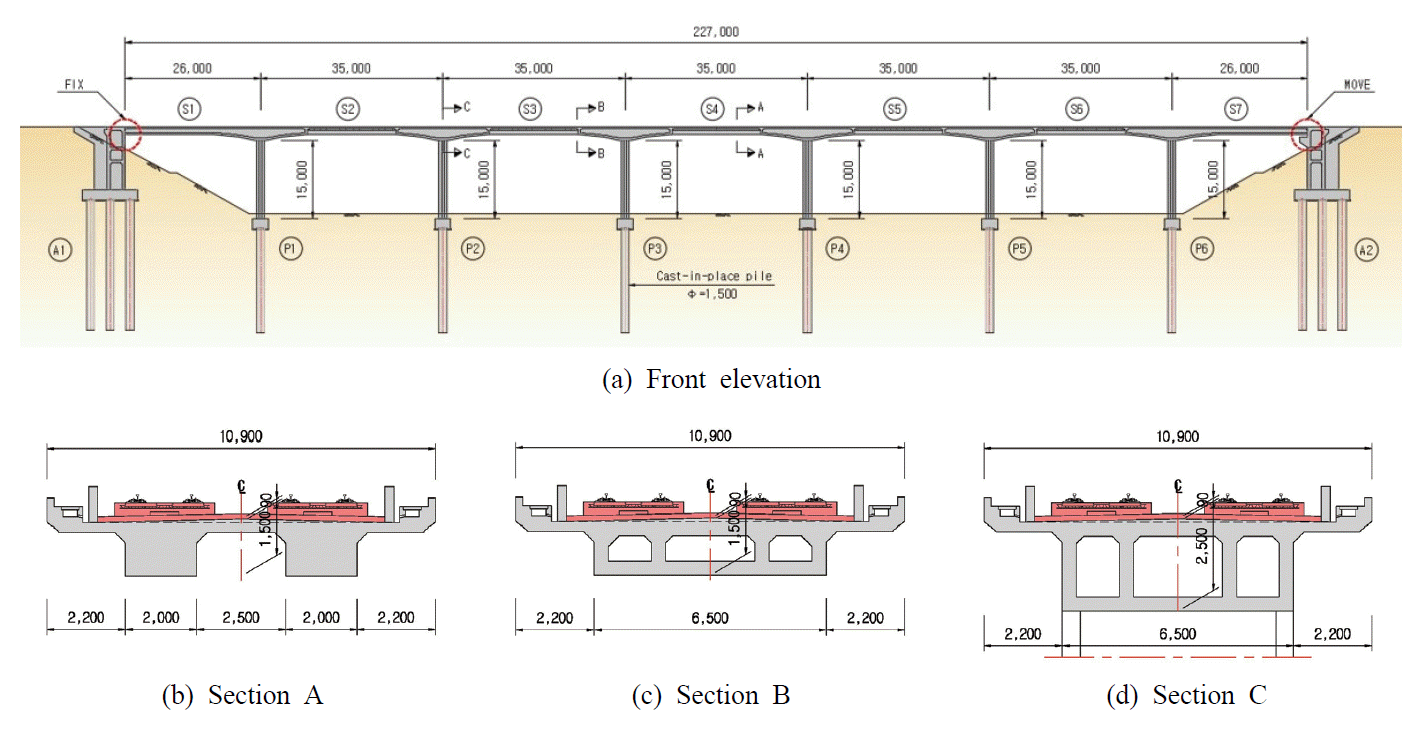
이 연구의 대상이 되는 완전일체형 교량은 Fig. 1(a)와 같이 각 지간은 26.0~35.0 m이고 총 7경간으로 구성되어 연장은 227 m에 달하며 교폭은 10.9 m인 철도교이다. 이는 국내 철도교설계기준(2016)에 의거하여 검토되었다. 앞서 언급된 바와 같이 하부구조와 상부구조는 서로 강결된 구조 형식이며, Fig. 1(a)에서 보이는 바와 같이 하부구조는 양단에 대칭으로 설치된 변위제어 교대와 그 사이 6개의 중간 교각으로 형성된다. 상부구조는 각 구간의 소요 강성과 형고에 따라 총 3가지의 프리스트레스트 콘크리트 거더로써 구현되는데 Figs. 1(b), 1(c) 및 1(d)와 같이 각기 박스형 단면이나 충실 단면을 갖는다. 상부구조와 하부구조의 단면제원은 각각 Table 1과 같고, 구성요소별로 사용된 재료특성은 Table 2와 같다.
교각의 강성이 감소할수록 하중 분담이 감소하는 것을 감안하여 교각의 기초는 현장타설말뚝 Φ1,500 3개를 교축직각방향으로 1열 배치하여 종방향 수평력 분담을 최소화하고, 변위제어 교대의 경우 다주 가구의 말뚝 배치로 종방향 수평력에 대해 저항하도록 계획하였다.
교대 강성에 따른 완전일체형 연속교량의 거동 특성 분석을 수행하였다. 교량에 재하되는 수평하중의 가장 지배적인 인자로 예상되는 지진하중을 적용하여, 교대 구조 및 강성에 따른 하부구조와 상부구조의 상호작용과 수평하중 분배특성 및 변위제어 효과를 정량적으로 평가하고자 한다. 이를 통해 변위제어 교대의 소요 강성과 규모, 수평변위의 적정 제한 수준을 결정하고자 한다. 이로부터 일체형 교량시스템 형성을 위한 목표성능의 정량적 도출이 가능해 질 것으로 기대되고, 순차적으로 주로 수직하중에 대해 저항하는 슬림형 교각의 단면도 추정될 수 있게 된다.
최대 수평하중(지진하중)에 의한 변위제어 교대를 포함한 교량시스템의 수평방향 및 횡방향 거동해석을 단일모드/다중모드 스펙트럼 해석법으로 진행하였다. 현재 우리나라 도로교 설계기준 한계상태설계법(2015)에서는 내진설계를 위한 기본적인 해석법으로 단일모드 스펙트럼 해석법을 사용하는 것을 기본으로 하고 있으며, 정밀한 해석이 요구되는 교량에 대해 다중모드 스펙트럼 해석법을 추천한다.
단일모드 스펙트럼 해석법은 하나의 진동모드만을 사용하는 스펙트럼 해석법으로, 교량을 교축방향과 교축직각방향에 대해 각각의 고유주기를 계산하여 간단하게 탄성력과 탄성변위를 구하고 교량에 적용할 등가정적 지진하중을 산정하는 방법이다. 단일모드 스펙트럼법에 의한 해석 시 설계하중의 결정에 쓰이는 탄성지진응답계수 Cs는 다음 식 Eq. (1)로 구한다.
여기서, 가속도 계수 A는 재현주기 1000년에 해당하는 0.154, 지반특성계수 S는 지반종류Ⅱ에 해당하는 1.2 값을 이용하였다. 교량의 주기는 다음 Eq. (2)와 같이 정해진다.
종방향 및 횡방향 지진에 의한 단일모드스펙트럼에 의해 평가된 단위길이당 등가정적 지진하중 pe는 다음 Eq. (6)으로 산정된다.
여기서, w(x)는 교량 상부구조와 이의 동적거동에 영향을 주는 하부구조의 단위길이당 고정하중이고, vs(x)는 균일한 등분포하중 p0를 적용하여 유한요소 해석 모델링을 통해 구한 정적처짐(변위)이다.
당해 교량시스템의 하부구조는 서로 상이한 강성을 갖는 변위제어 교대와 교각이 일체화된 것이어서 교량 각 위치의 종방향 변위 vs(x)는 유한요소모형을 이용한 수치해석을 통해 우선 구해야 한다. 이때 전체 교량의 등가강성 개념을 적용하여 평균적으로 적용할 수도 있다. 위와 같이 산정된 등가정적지진하중을 유한요소모형에 교축방향 및 교축직각방향으로 적용하여 수평 변위, 밑면전단력 및 전도모멘트 등 지진응답을 분석한다.
다중모드 스펙트럼 해석은 여러 개의 진동모드를 사용하는 스펙트럼 구조해석법으로, 일체형 교량의 교대와 교각이 균일하지 않기 때문에 강성차이의 영향을 살펴보기 위해 비교 해석하였다. 교량의 모델링은 그 구조물의 강성과 관성효과를 설계에 가깝게 하기 위해 3차원 공간뼈대구조물로 모델링하며, 각 모드의 복합연계효과 및 최종응답의 기여도를 결정하기 위한 공간뼈대요소의 선형 동적해석을 수행해야 한다. 따라서 교량 모델링은 각 연결부와 절점이 6개의 자유도를 가진 3차원 공간뼈대구조물로써 모형화하였으며, 각 부재별로 명시된 질량을 고려하여 관성효과를 포함한다. 응답해석 시 고려되는 모드 수는 총 30개이며, 부재의 단면력과 변위는 개별모드로부터 각각의 응답에 90% 이상의 질량 참여율을 확보하였다. 교대 강성에 따른 변수해석적 연구의 유한요소 수치해석은 범용구조해석프로그램인 Abaqus를 이용하여 진행하였다.
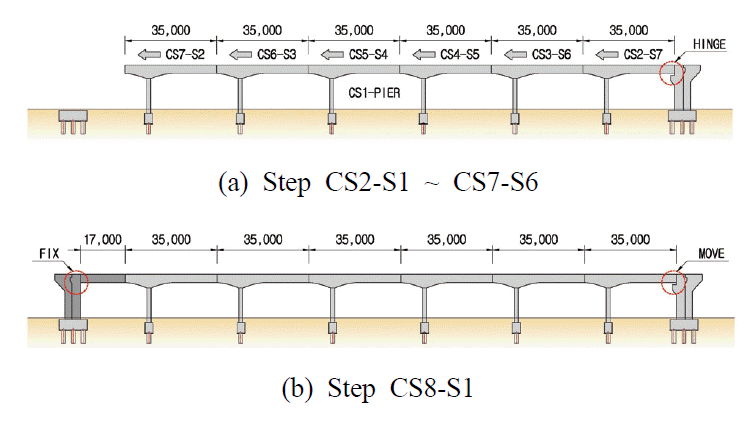
완전일체형 연속교 개발을 위한 교량의 거동 특성 분석을 위한 시공 단계별 변수해석이 요구된다. 이에, 제작단계를 고려한 수치 해석적 모형을 수립하였다. 변수해석을 위한 콘크리트 타설 순서 및 교대부 지점 조건은 Fig. 3과 같으며, 이에 따른 시공단계별 수치 해석을 수행하였다. 시공단계에 따른 일체식 교량의 유한요소해석 모델링은 주거더와 슬래브 전체를 6자유도 보요소로 Midas Civil을 이용하여 수행하였으며, 작용하중은 자중, 2차고정하중, 충격을 고려한 열차하중, 크리프 및 건조수축 등을 고려하였으며 보요소에 긴장재를 모델링하여 해석을 수행하였다. 완성계 모델에서는 자유단인 교대 A2를 시공 시 가고정점(hinge)으로 적용하여 상부 거더 완료시까지 크리프 및 건조수축에 의한 변위를 교대 A2방향으로 유도하였으며, 최종 단계에서는 교대 A1을 고정시키고 교대 A2를 다시 자유단으로 변경하여 공용 중 크리프 및 건조수축에 의한 변위를 교대 A1방향으로 유도함으로써 크리프 및 건조수축에 의한 구조물의 응력을 최소화하였다.
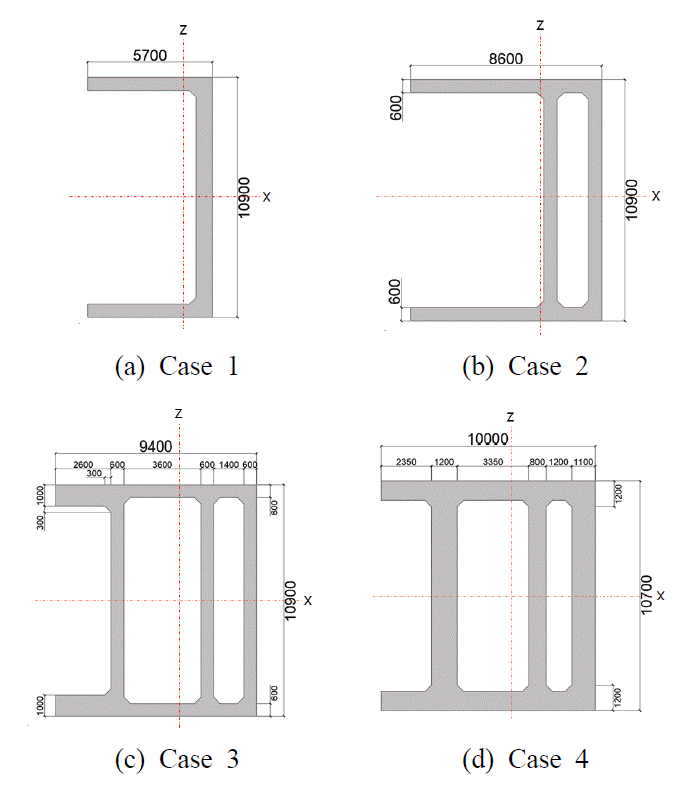
변위제어 교대의 소요 강성 기준을 정립하고 구조성능을 검증하기 위해 교대의 구조 및 강성에 따른 변수해석 모델을 수립하였다. 유한요소해석 모델링은 범용 구조해석 프로그램인 ABAQUS를 이용하여 수행하였으며, B31 보요소를 이용하여 Fig. 4와 같은 프레임구조의 유한요소 모델을 구성하였다. 각 지점의 경계조건은 Table 5와 같이 고정지지 조건을 적용하였고, 하중은 교축방향(종방향)거동의 검토 시에는 x-축 방향으로, 교축직각방향(횡방향) 거동의 검토를 위해서는 z-축 방향으로 균일한 등분포하중을 재하하였다. 토사는 모래부터 자갈까지 다양한 크기를 형성하고 있으며, 그 중 강우로 인해 배수로로 유입되어 퇴적된 토사의 입자를 명확히 규정짓기에는 어려움이 있다. 또한, 다양한 토사분류 기준에서도 대략적인 직경만을 제시하였을 뿐 명확한 크기에 대한 기준은 제시되지 않았다.
완전일체형 연속교의 기본 설계안은 콘크리트 부재에 작용하는 인장응력을 최소화하고 시공성의 향상을 고려해서 상기 Table 4와 같이 정해졌다. 정해진 제작단계에 따른 시공단계별 선형해석을 수행하였다. 해석 모델링은 Fig. 5와 같이 기초의 강성을 적절히 고려하기 위해 현장타설말뚝을 모델링에 반영하였으며, 타설 순서와 양생 시간 등이 반영될 수 있도록 시공단계별 하중 조건을 구성하였다.
각 응력의 평가 결과는 Tables 6 and 7에 제시된 바와 같다. 단계별로 거더 타설 및 긴장력의 도입에 따른 프리스트레스 도입 시 압축강도 30 MPa의 허용압축응력 16.5 MPa, 허용인장응력 2.739 MPa의 만족 여부를 확인하고, 사용하중(열차하중 및 온도하중) 재하 시 상부 거더의 무인장화(허용 인장응력 0 MPa)가 가능하도록 검증하였다.
시공단계별 해석결과를 살펴보면 첫 번째 경간 S7의 타설 및 긴장력의 도입 시 단면에 가장 큰 인장응력이 발생하나 이는 시공 중 허용응력 범위 내에 분포하고 있으므로 구조물의 안전에는 영향이 없을 것으로 판단된다. S6에서 S2타설까지는 S7의 타설과 유사한 응력 분포가 형성되며, 구조물의 시종점부의 지점 조건 변경 및 최종 긴장작업이 완료되는 CS8-S1 단계에서는 압축응력의 증가로 거더의 무인장화가 형성되며, 이때 압축응력은 허용응력을 만족한다. 최종 사용 하중 단계에서는 열차하중 및 온도하중의 영향으로 거더상단의 압축응력은 감소하나, 거더 하단의 압축응력이 미소하게 증가된다. 이는 허용압축응력인 16 MPa 범위 이내에 해당되므로 관련 기준을 충족한다.
상부 거더와 하부 구조가 강결된 라멘 구조는 시간 종속적 응력인 크리프 및 건조 수축에 의해 하부구조의 수평력 및 전도 모멘트가 크게 발생하며, 이를 최소화하기 위해 시공단계별로 교대부지지 조건을 변경하여 해석을 수행하였다. 크리프 및 건조수축에 의한 시공단계별 하부구조에 나타난 단면력은 Fig. 6과 같으며, CS2-S7~CS7-S2 시공단계와 CS8-S1 시공단계의 단면력 방향이 서로 상반되는 것을 볼 수 있다. 이는 지점조건 변경에 의한 영향을 적절히 반영된 것으로써 시공단계별 지점조건의 변경에 의해 하부구조에 발생하는 단면력을 줄일 수 있으므로 이와 같은 효과를 적절히 활용하면 하부구조 소요 단면의 저감이 기대된다.
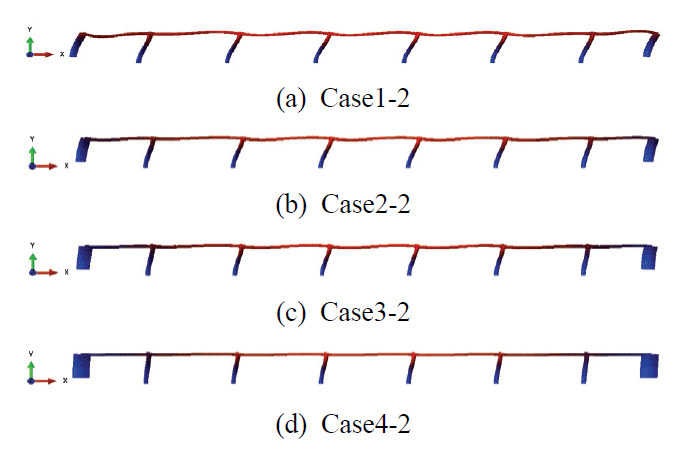
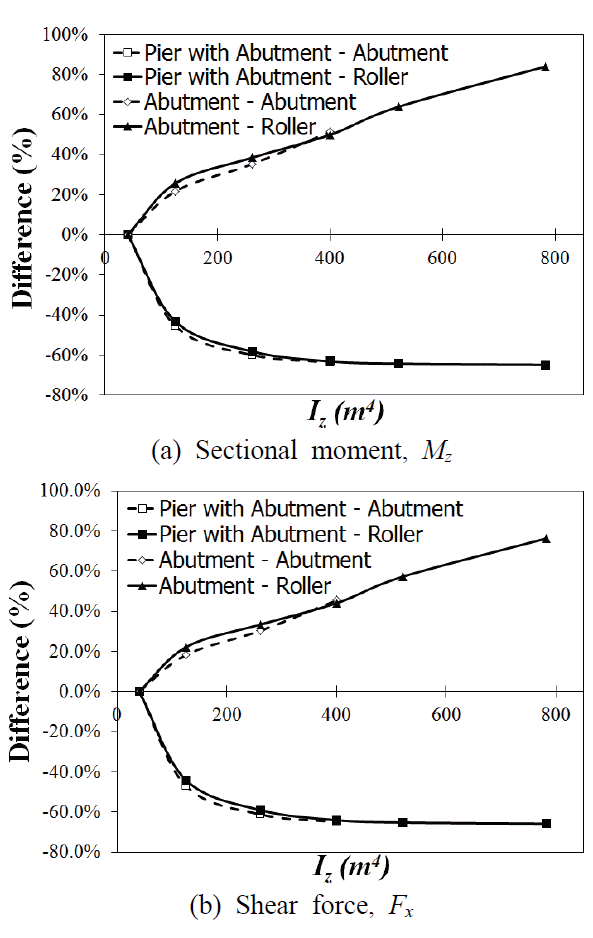
종방향 거동을 유효지진하중을 재하하는 유한요소해석을 수행하여 Fig. 7과 Table 8과 같은 변위제어교대의 구조 및 강성에 따른 교량시스템의 구조적 거동형상 및 변위와 밑면전단력, 모멘트 등 수평하중의 분배 경향을 확인하였다. 이는 단일모드 스펙트럼 해석법에 의거하여 평가된 것으로, 수평지진하중에 의한 각 Case에 따라 교각과 교대의 단면력 발생량을 분석하여 Fig. 9의 도표에 각각 나타내었다. 유한요소해석을 수행하였으며, Case 1~6은 일측교대 일체형 교량(Abutment-Roller), Case 1-2~4-2는 양측교대 일체형 교량(Abutment-Abut ment)이다.
Fig. 8(a)는 각 Case별 교대의 교축직각방향축(z축)에 대한 휨강성 차이를 나타내며, Case 1을 기준으로 단면2차모멘트(Iz)를 최소 2배에서 18배로 증가시켜가면서 변수연구를 수행하였다. 이와 같이 교대의 교축직각방향 단면2차모멘트에 따라 변수연구를 수행한 결과, 교대에 발생하는 최대 전단력과 모멘트는 교각에 비해 10배에서 최대 24배 정도 크게 작용하는 것으로 나타났다. 이에 따른 교축방향 변위응답을 Fig. 8(b)에서 볼 수 있는데 교대의 강성이 증가함에 교대와 교각의 변위가 줄어든다. 교각의 단면에 작용하는 전도모멘트는 Fig. 9(a)에 보이듯이 줄어드는 경향을 보이다가 Case 4에서 점차 수렴하여 최대 65% 감소한다. 일례로, Case 1과 비교했을 때, Case 4에서 63% 차이로 다소 급격히 줄어들다가 Case 6에서는 불과 65% 정도가 된다. 교각의 밑면전단력도 유사한 감소 경향을 보이는데 Fig. 9(b)에서 볼 수 있듯이 Case 4에서 점차 수렴하여 최대 66% 감소한다. 따라서 구조적 응답이 수렴된 범위 이상으로 교대의 강성(Iz)을 늘리는 것은 무의미해 보이며, 오히려 질량 성분의 증가로 불리한 결과를 초래할 수도 있다. 또한 변위제어 교대의 z축 휨강성이 교량 전체의 수평 거동에 대해 민감한 영향을 갖는 설계인자임을 알 수 있으며, 해당 축에 관한 단면2차모멘트 Iz가 200 m4 수준에 도달하면 교각에 발생하는 밑면전단력 및 전도모멘트가 각각 60% 가까이 감소하면서 수렴구간을 형성한다. 즉, Case 2와 3의 범위에서 구조적 응답의 수렴구간이 나타나므로, 이를 감안하여 적절히 채택하면 교량의 수평변위를 효과적으로 제어하고 그에 상응한 수준으로 교각의 단면과 상부구조의 형상을 슬림하게 줄일 수 있을 것으로 기대된다.
유사하게 양측교대 일체형 교량 모델은 Case1-2를 기준으로 교대의 단면2차모멘트를 최소 2배에서 10배까지 증가시켜가면서 변수연구를 진행하였다. 이에 따른 교축방향 변위 응답은 Figs. 7 and 8(c)에서 볼 수 있는데, 교대의 강성이 증가함에 교대와 교각의 변위가 줄어든다. 교각의 단면에 작용하는 전도모멘트와 밑면전단력은 각각 최대 64% 및 65%까지 감소한다. 일측교대를 적용한 경우(Abutment-Roller)와 비교해 보면 교대강성 증가에 따라 거의 유사한 수준으로 감소하는 경향을 볼 수 있다. 교각의 변위는 양측교대가 일측교대의 경우에 비해 1.5~2배 정도 작다.
단일모드스펙트럼 해석(SSA) 및 다중모드스펙트럼 해석(MSA) 등 각기 해석법에 따른 결과를 비교하였다. Table 9를 보면 수평변위량은 MSA에 비해 SSA방법이 10% 내외의 오차범위로 다소 크게 평가하고 있다. 최대모멘트와 밑면전단력은 교대에서는 SSA가 MSA에 비해 다소 보수적으로 평가하고 있으나, 교각에서는 오히려 SSA보다 MSA가 과다한 평가를 하고 있다. 따라서 슬림한 교각의 설계에서는 다중모드 스펙트럼 해석법을 따르는 것이 바람직할 것으로 보인다.
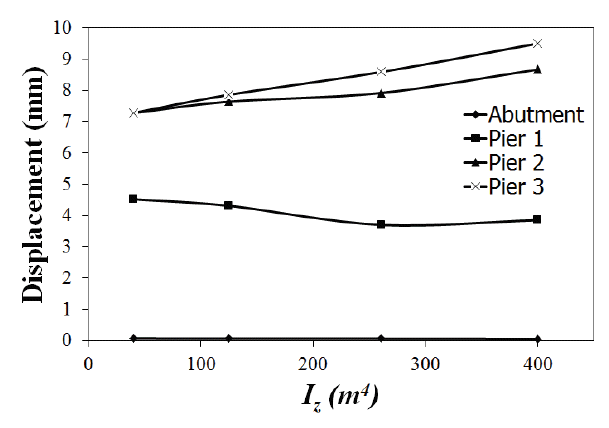
완전일체형 교량에 횡방향으로 유효지진하중을 재하했을 때 수평방향 거동은 Fig. 10과 같고, 교대 강성에 따른 교각과 교대에서의 변위응답은 Fig. 11에서 볼 수 있다. 교각과 교대의 단면력은 Table 10과 Fig. 12의 도표에 각각 나타내었다.
앞서 설명된 바와 마찬가지로 교대의 단면2차모멘트(Iz)를 최대 18배까지 증가해가며 변수연구를 수행하였다. Fig. 12(a)에서 볼 수 있듯이 교대에 작용하는 전도모멘트는 종방향 거동과 같이 유사한 추세로 최대 109%까지 증가했고, 교각에서의 변동은 상대적으로 그 차이가 크지 않았다. 교각의 전도모멘트는 Fig. 12(a)에서 보이듯이 Case1-2를 기준으로 해서 그 차이가 15% 내외 정도였다. 교각의 밑면전단력에서도 모멘트의 변동양상과 유사한 경향을 보인다. 밑면전단력도 Case1-2에 비교하여 교대에서는 최대 125% 늘어나지만, 교각에서는 Case1-2를 기준으로 해서 15% 내외 정도였다.
구조적 특성상 횡방향 변위와 단면력은 교대로부터 멀리 떨어진 위치일수록 증가하며, Fig. 11에서 보이는 바와 같이 교대강성이 증가하더라도 Pier3과 같이 가장 멀리 떨어진 위치의 교각에서는 오히려 단면력이 늘어난다. 이는 스펙트럼해석법에서 교대 질량의 증가를 균일하게 모사하기 때문인 것으로 유추된다. 보다 엄밀한 해석을 수행하면 다소 달리 평가될 수도 있지만 일체형 교량이더라도 교대강성의 횡방향 거동에 대한 제어에 한계는 자명한 것으로 판단된다. 이에 따라, 완전일체형 교량이더라도 횡방향 거동에 대한 교각의 소요강성은 기존의 교각과 유사한 수준을 유지해야 할 것으로 사료된다. 또는 경간 중앙에 위치한 교각의 횡방향 강성을 높이는 것도 횡방향 거동을 저감하는 데 효과가 있을 것으로 추정된다.
이 논문에서는 완전일체형 철도 연속교의 시공단계별 단면력과 교대 강성에 따른 수평하중 분배특성을 수치해석적으로 분석하였다. 국내 설계기준에서 예상되는 지진하중효과에 의거한 최대 수평하중을 적용하여 상부구조와 변위 제어교대 및 교각 간의 상호작용을 확인하였다. 교대의 강성에 따른 변수해석을 통해, 교각의 전도모멘트와 밑면전단력 값이 선형적으로 감소하다가 일정한 수준으로 수렴하는 경향을 확인하였다. 즉, 효과적인 변위제어를 위한 적정한 교대강성이 도출되었다. 이를 감안하여 교량의 수평변위를 효과적으로 제어하고 그에 상응한 수준으로 교각의 단면과 상부구조의 형상을 날렵하고 슬림하게 줄인 구성안이 제시되었다. 교대와 상부구조물의 연결조건을 시공단계별로 달리하고 변위제어 교대와 강연선을 적절히 배치하면 국내 철도설계기준이 제시하는 허용응력을 만족하는 것을 확인하였다. 추후, 궤도-교량 상호작용, 비선형 거동 및 지반과의 상호작용을 고려하는 엄밀한 해석기법을 통해 비교연구를 수행하면 완전일체형 교량의 유리한 특성을 극대화하는 방안과 현행 설계기준의 합리적인 적용 방안 등이 면밀하게 정립될 수 있을 것으로 사료된다.
Table 1.
Dimensions of Structures
Table 2.
Properties of Concrete
| Type | fck (MPa) | E (MPa) | G (MPa) | w (kN/m3) |
|---|---|---|---|---|
| Super-structure | 40 | 30008 | 12857 | 24.5 |
|
|
||||
| Sub-structure | 30 | 27537 | 11798 | 24.5 |
Table 3.
Dimension and Properties of Abutment for Parametric Study Cases
Table 4.
Construction Procedure of Fully Integral Bridge System
Table 7.
Construction Procedure Stress Reiview ((+)tension, (-)compression, MPa)
Table 8.
Parametric Analysis Results in the Longitudinal Direction
Table 9.
Comparison of Response Spectrum Analysis Methods
Table 10.
Parametric Analysis Results in the Lateral Direction
References
Ahn, J.H., Yoon, J.H., Choi, W.J., Jang, J.W., Kim, S.H., and Lee, S.W. (2009). Application and Behavior of Integral Abutment Bridge on Multi-span PSC Girder Bridge. Proceedings of Korean Society of Civil Engineers Conference. pp. 138-141.

Ahn, J.H., Yoon, J.H., Kim, S.H., and Kim, J.H. (2010) Evaluation on Behavioral Characteristics of PSC Integral Abutment Bridge. Journal of Korean Society of Civil Engineers, Vol. 30, No. 4A, pp. 361-373.

Korean Construction Standards Center (KDS 24 17 11) (2016). Guidelines for the Bridge Seismic Design Standard (LSD).

Korean Institute of Bridge and Structural Engineers (2015). Highway Bridge Design Standard Explanation (LSD).

- TOOLS
-
METRICS

-
- 1 Crossref
- 4,789 View
- 92 Download
- Related article in KOSHAM