1. 서 론
공용중인 철근콘크리트 구조부재의 방재 성능은 작용하중과 단면의 저항강도를 비교하여 안전성을 확보하고 있는지 검토하는 것을 평가의 기본 원칙으로 한다. 이와 함께 사용하중 단계에서 발생하는 처짐, 균열폭, 피로 등이 허용하는 사용한계 범위내에 존재하는지 조사하고 계산하는 사용성능 검토도 반드시 수행해야 한다. 콘크리트 구조물의 성능 진단이나 평가 시 균열에 대한 검토를 규정하는 중요한 이유들은 심미적 안정성, 유체의 차폐를 위한 수밀성, 철근의 부식 방지를 위한 내구성 및 콘크리트 재료의 불확실성 등에 있다. 그러나 균열과 철근 부식 또는 심미적 안정성 관점에서의 원인에 대한 명확한 자료들이 상대적으로 부족하기 때문에 콘크리트구조기준(이하, KCI-12), 도로교설계기준(한계상태설계법)(이하, KHBDC)의 설계기준에서는 강도 안전성에 비하여 비교적 간단한 규정들로 기준을 제시하고 있다(KCI, 2012; KRA, 2012, 2015; Kim, 2014; KIBSE and KBRC, 2015).
현행 설계기준에서는 균열과 관련된 사용성능 검토에 대해서 균열폭을 계산하여 허용 균열폭의 초과 여부를 검증하는 직접 균열제어와 철근의 인장응력 수준에 따라 균열폭 계산없이 한계 균열폭 이내에 있다고 간주할 수 있는 최대 철근간격과 철근지름으로 규정하는 간접 균열제어로 구분한다.
직접 균열제어와 관련하여 철근콘크리트 구조물의 균열폭 계산을 위한 역학적인 개념은 균열간격 내에서 발생하는 두 재료의 변형률 차이의 누적합으로 정의되며, 이를 계산하기 위해서는 철근과 콘크리트의 부착특성에 따른 균열간격과 인장강화효과(tension stiffening effect)를 고려한 철근과 콘크리트의 변형률을 각각 계산해야 하는 복잡한 과정이 필요하다.
이와는 다르게 간접 균열제어에 따른 최대 철근간격에 대한 현행 설계기준의 규정은 KHBDC의 경우 2차식 형태의 인장강화효과 모델을 이용함으로서 단면치수에 상관없이 일정한 값을 얻지 못하기 때문에 단면깊이의 변화를 추가적으로 고려해야 한다. KCI-12의 경우 ACI 318에서 규정하는 Frosch (1999)가 제안한 경험적 균열간격 모델을 차용하므로 균열간격이나 인장강화효과와 같은 철근콘크리트 부재의 균열거동과 부착특성을 반영하지 못한다는 단점이 있다.
한편, 콘크리트구조설계기준(KCI, 2007), KCI-12 (KCI, 2012), ACI 318(ACI Committee 318, 2008), CEB-FIP Model Code 1990 및 Eurocode 2(이하, EC 2; CEN, 2002) 등의 설계기준에서 각각 규정하고 있는 균열폭, 균열간격, 인장강화효과에 대한 식들을 이용하여 철근간격 또는 철근지름을 각각 유도하고, 이로부터 철근 응력 단계별 값들을 각각 계산하여 적용성을 검토하거나 간접 균열제어 방법을 제안한 연구가 수행되었다(Choi and Kim, 2011, Min, 2012). 그러나, 이들 연구에서는 KHBDC에서 규정하는 최대 철근간격이나 철근지름을 직접적으로 제시하지 못하고, 현행 설계기준의 간접 균열제어 규정에 대한 적용성 검토, 산정식 유도 및 정성적 모델만을 제안하였다.
이 연구에서는 대표적인 철근콘크리트 구조물인 보를 기준으로 사용성능 진단 및 평가에 중요한 역할을 하는 균열에 대해서 직접 계산을 하지 않고도 허용 균열폭 초과 여부를 판정할 수 있는 간접균열제어 규정인 최대 철근간격을 새롭게 제안하는 것을 목표로 한다. 이를 통하여 KHBDC와 KCI -12의 단점들을 보완할 수 있도록 균열거동과 부착특성을 반영하고, 단면 깊이에 대한 추가적인 보정이 필요 없으며, 콘크리트 압축강도 증가를 반영할 수 있는 수정된 보정계수를 도입하여 간접 균열제어에 의한 사용성능 평가의 적용성을 개선하였다.
2. 균열제어 규정의 고찰
2.1 직접균열제어
2.1.1 균열폭 기반이론
2.1.2 설계기준 규정
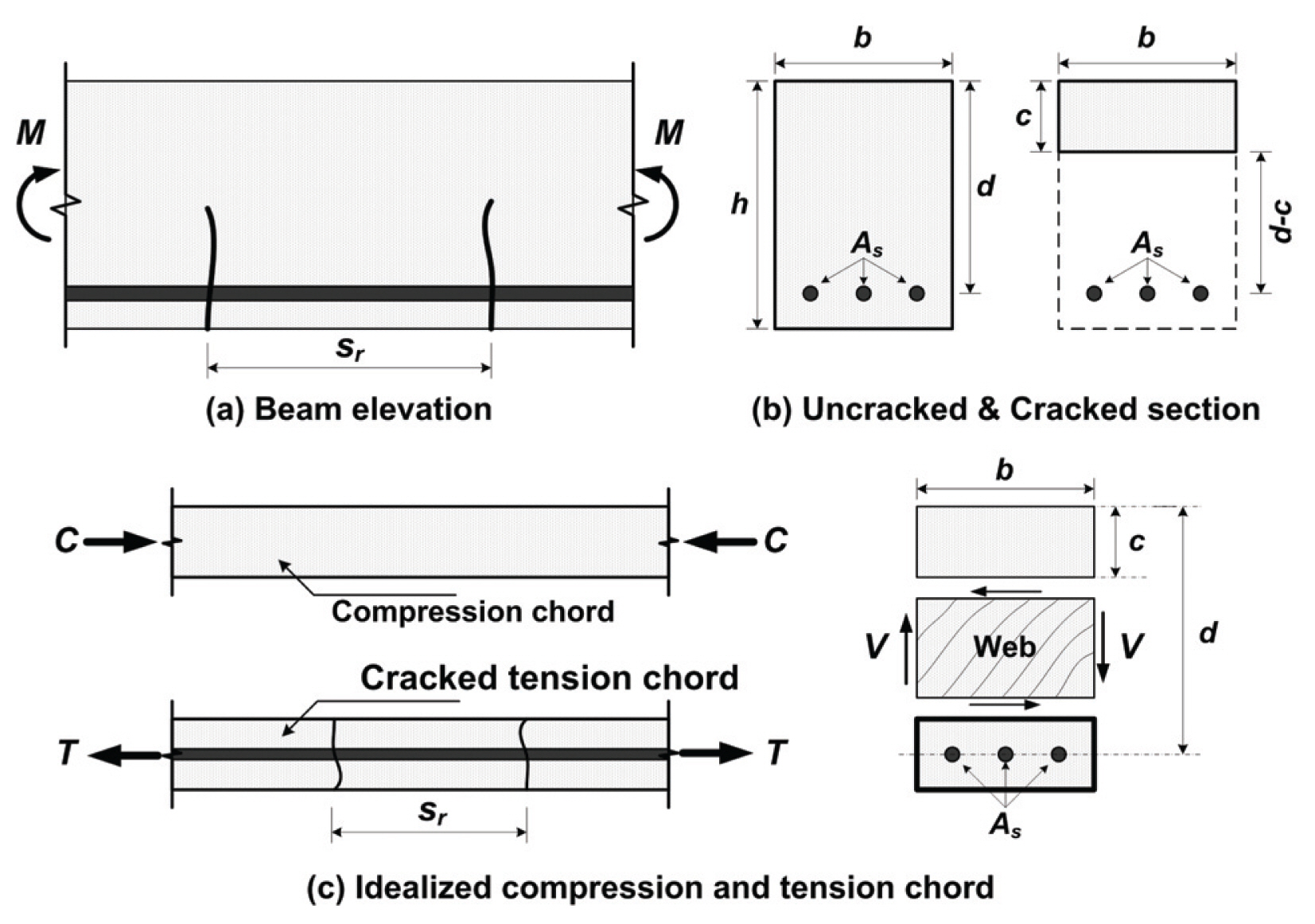
KCI-12와 KHBDC에서는 Eq. (1)을 기반이론으로 하여 Fig. 1(d)와 같이 평균변형률 개념을 이용하여 균열폭 계산식을 규정한다. 즉, 인접한 균열 사이에서의 철근 변형률 εsm과 콘크리트의 변형률 εcm의 차이와 전달길이로부터 정의되는 최대 균열간격 sr, max 또는 평균 균열간격 Sr, m을 곱하여 설계균열폭 wk를 계산하도록 다음과 같이 규정한다.
여기서, Kst는 KCI-12에서 규정하는 균열폭 평가계수로서, 평균 균열폭일때는 1.0, 최대 균열폭일때는 1.7을 적용한다. 따라서, KCI-12의 경우에는 균열폭 평가계수의 적용에 따라 최대 및 평균 균열폭을 모두 계산할 수 있다.
Eq. (2)대해서 철근과 콘크리트의 평균 변형률 차이는 인장강화효과를 이용하여 KHBDC에서는 1차식으로, KCI-12에서는 2차식 형태로 다음과 같이 정의한다.
여기서, fso는 균열면에서 철근응력(MPa), fsr은 균열 발생 직후 균열면에서 계산한 철근응력(MPa), fct는 콘크리트 평균 인장강도(MPa), Es는 철근의 탄성계수(MPa), n은 탄성계수 비이다. β1은 부착특성 계수로서 이형철근이면 1.0, 원형철근이나 강연선이면 0.5이다. β2은 하중조건에 따른 계수로서 반복하중이면 0.5, 그 외의 경우 1.0이다. ni는 콘크리트 초기접선탄성계수에 대한 철근 탄성계수의 비이다.
균열간격 sr은 Fig. 1(d)에 해당하는 균열안정화단계를 기준으로 KCI-12에서는 Eq. (4a)와 같은 평균 균열간격 sr, m으로, KHBDC에서는 최대 균열간격 sr, max로서 2012년에는 Eq. (4b), 이후 개정된 2015년에는 Eq. (4c)로서 다음과 같이 정의한다. 그런데, KHBDC의 균열간격은 EC 2와 동일한데, Eq. (4b)는 Part 2, Eq. (4c)는 Part 1에 해당한다.
여기서, db는 철근직경(mm), cc는 피복두께(mm), k1은 철근의 부착특성 계수로서 이형철근이면 0.8, 원형철근이면 1.6이고, k2는 부재의 하중작용에 따른 계수로서 휨일 때 0.5, 순수 인장일 때 1.0이다.
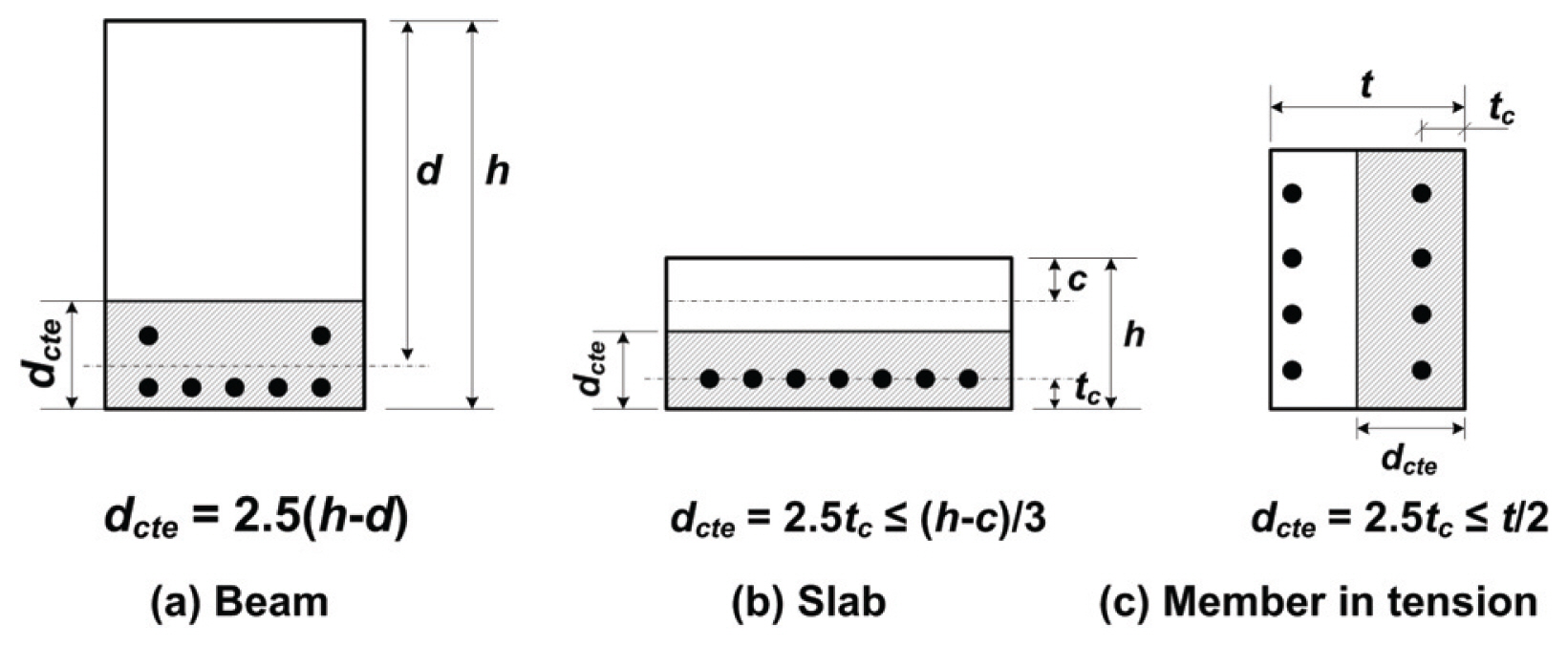
그런데, Eqs. (3)과 (4)는 Figs. 2(a)와 2(b)에 보인 것과 같이 균열이 발생한 철근콘크리트 부재의 인장영역 일부를 Fig. 2(c)와 같이 인장 현재(tension chord)로 이상화하여 앞에서 설명한 일축인장부재의 거동을 적용한 것이다. 따라서 이 식을 단면 깊이에 따라 응력과 변형률이 변하는 휨부재의 인장 현재에 적용하기 위해서는 Fig. 2(c)에 보인 인장철근을 포함하는 인장 현재에 대해서 Fig. 3과 같이 유효 인장면적의 깊이 dcte를 갖는 음영으로 표시한 콘크리트 유효 인장단면적 Acte로 정의해야 한다. 따라서 유효 인장철근비 ρe는 콘크리트 유효 인장단면적을 이용하여 다음과 같이 정의할 수 있다.
여기서, b는 단면폭(mm), As는 인장철근 단면적(mm2)이다.
2.2 간접균열제어
앞 절에서 설명한 바와 같이 균열폭을 직접 계산하고 한계값과 비교하여 사용성을 검증하는 것은 상당히 복잡한 계산과정을 거쳐야 하는 어려움이 있다. 이러한 문제점을 해결하기 위하여 실제 사용성능 평가 및 설계 실무에서는 한계 균열폭 이내에 있다고 간주할 수 있는 일정 기준을 만족한다면 균열폭 계산을 통한 검증 과정을 피할 수 있는 간접균열제어를 주로 이용한다. 즉, 최소 철근량 조건을 만족하고, 배치된 철근이 최대 지름 및 간격 중 하나를 만족한다면 균열폭이 허용 한계값 이내에 있다고 간주할 수 있다.
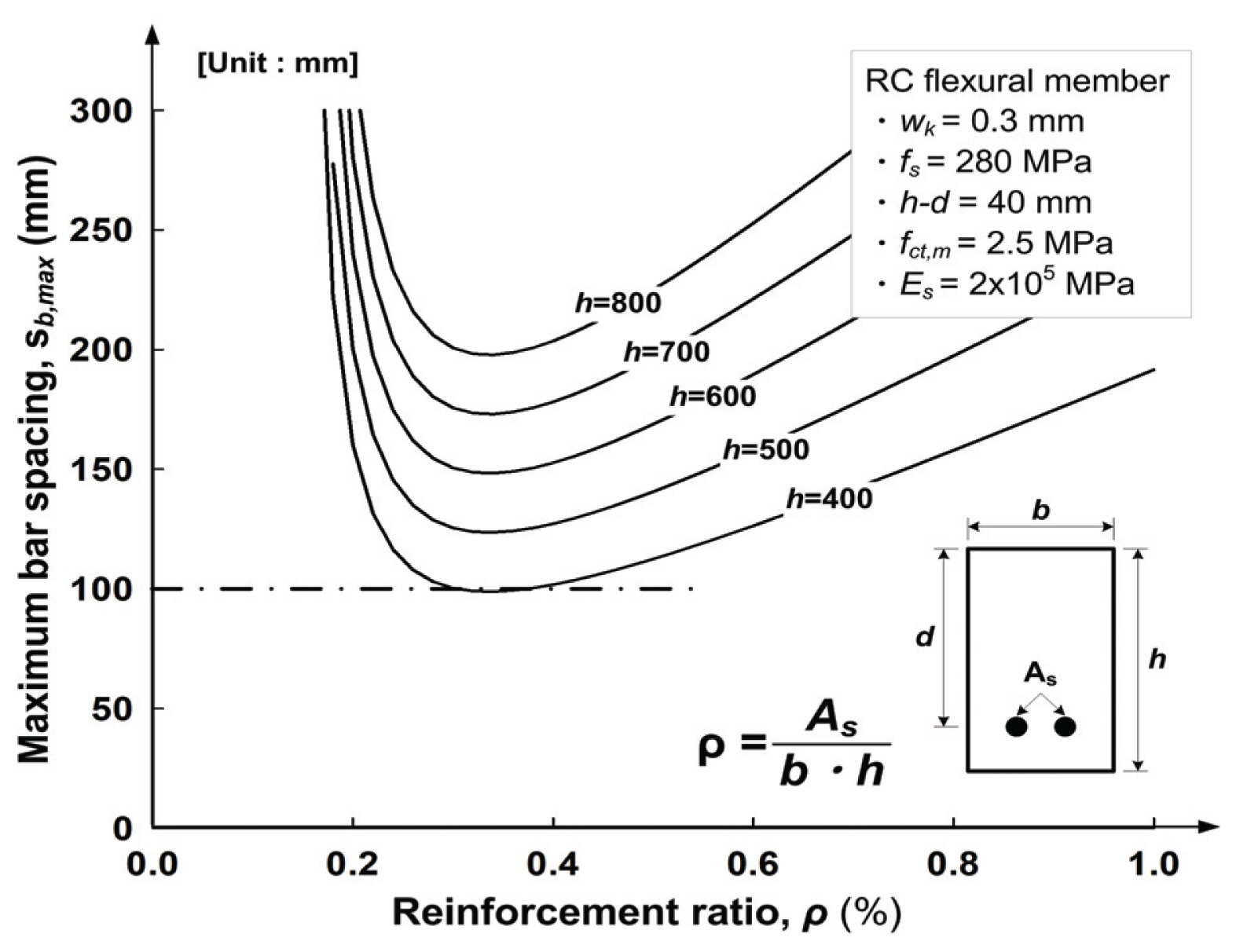
이를 위하여 KHBDC에서는 EC 2 및 Euro-Design Handbook (Eibl, 1994)과 동일하게 앞 절의 균열폭 계산식을 철근 지름과 철근 간격에 대한 식으로 변환한 후, 철근콘크리트 구조물의 한계균열폭 0.3mm를 만족하도록 Fig. 4와 같은 방법에 의해 철근의 각 응력 수준에서 필요한 최대 지름과 간격을 Table 1과 같이 각각 규정하고 있다.
Euro-Design Handbook에 따르면 이 표의 값들은 사각형 단면 부재를 기준으로 콘크리트 인장강도 fct가 2.5 MPa(fck = 27 MPa에 해당)이고, 피복두께를 0.1h(=h-d)로 고정한 후, 미리 정한 철근응력 수준마다 단면 깊이 h를 변화시켜가면서 한계균열폭에 해당하는 철근간격을 각각 계산하여 정리한 것이다. 그런데, 이렇게 계산된 철근간격은 Fig. 4에서 보인 것과 같이 단면의 깊이에 따라 값이 변화한다.
따라서 이에 대한 보정이 필요한데 KHBDC에서는 이에 대한 별도의 규정이 없는 반면, EC 2에서는 동일한 방법으로 산정된 최대 철근지름에 대해서 다음과 같은 식을 이용하여 단면 깊이와 콘크리트 강도 변화에 대한 보정을 하도록 규정하고 있다. 따라서 최대 철근간격 sb, max도 이와 동일한 조건에 따른 보정이 필요하다고 하겠다.
여기서, s*b, max는 Table 1에 따른 최대 철근간격이고, hcr은 균열 발생에 따른 인장영역의 깊이이고, h와 d는 Fig. 3(a)에 보인 단면 깊이와 유효깊이이다. 그리고 kc는 다음 식으로 정의되는 균열 발생 직전의 단면 내 응력분포상태와 균열 발생 직후의 팔길이 변화를 반영하는 계수이다.
여기서, fc는 콘크리트 단면응력(MPa), k1은 축력이 응력분포에 미치는 영향을 반영하는 계수로서, 축력이 압축력이면 1.5, 인장력이면 2h*/3h를 적용하고, h*는 부재 높이 h < 1.0m 이면 h* = h이고, h ≥ 1.0m 이면 h* = 1.0m 을 적용한다.
이와는 다르게 KCI-12에서는 간접균열제어에 대해서 콘크리트 인장연단에 가장 가까이에 배치된 철근의 중심간격 s가 다음 두 식에 의해 계산된 값 중에서 작은값 이하로 되도록 규정한다. 단, 부록 Ⅲ의 규정에 따라 균열폭을 직접 계산하는 경우에는 이 규정을 따르지 않을 수 있다.
여기서, kcr은 부록 Ⅲ에서 정의된 건조환경에 노출되는 경우에는 280, 그 외의 환경에 노출되는 경우에는 210이다. cc는 인장철근의 표면과 콘크리트 표면 사이의 최소 두께이다. fs는 사용하중 상태에서 인장연단에 가장 가까이에 위치한 철근의 응력이다.
이상과 같이 고찰한 설계기준별 균열제어 규정들을 Table 2에 정리하였다. 균열폭을 계산하여 허용 균열폭과 비교하는 직접 균열제어는 KCI-12, KHBDC 및 EC 2에서 도입하고 있는데, 이들 규정은 균열간격 및 철근과 콘크리트의 평균변형률 차이에 대한 각 기준별 식을 이용하여 균열폭을 직접 계산할 수 있도록 한다. 그리고, 간접 균열제어는 ACI 318을 포함하여 모든 설계기준에서 도입하고 있는데, ACI 318과 KCI-12에서는 Eq. (8)에 의한 철근간격으로, KHBDC와 EC 2에서는 Table 1과 같은 철근 응력 수준별 최대 철근간격 및 철근지름으로 규정하고 있다.
3. 철근간격 산정식 유도
이 연구에서 제안하는 최대 철근간격은 Eq. (2)의 균열폭 계산식을 철근간격에 대한 식으로 유도하여 산정할 수 있다. 먼저, KHBDC에서 규정하는 Eq. (3a)의 인장강화효과를 고려한 철근과 콘크리트의 변형률 차이와 Eq. (4b)의 균열간격을 고려하여 균열폭 계산에 따른 허용균열폭 조건을 다음과 같이 정의한다.
Eq. (9)에서 균열간격을 EC 2-Part 2에서 규정하는 Eq. (4b)로 적용한 이유는 앞 절에서 설명한 것과 같이 최대 철근간격 산정 시 0.1 h로 피복두께가 고정되어 있으므로 직접적인 변수로 선정하기가 어려우며, 최대 철근간격 산정을 위한 계산식을 단순화하기 위함이다.
다음으로, 균열폭에 대한 Eq. (9)를 철근지름 db의 항으로 정리하면 다음과 같다.
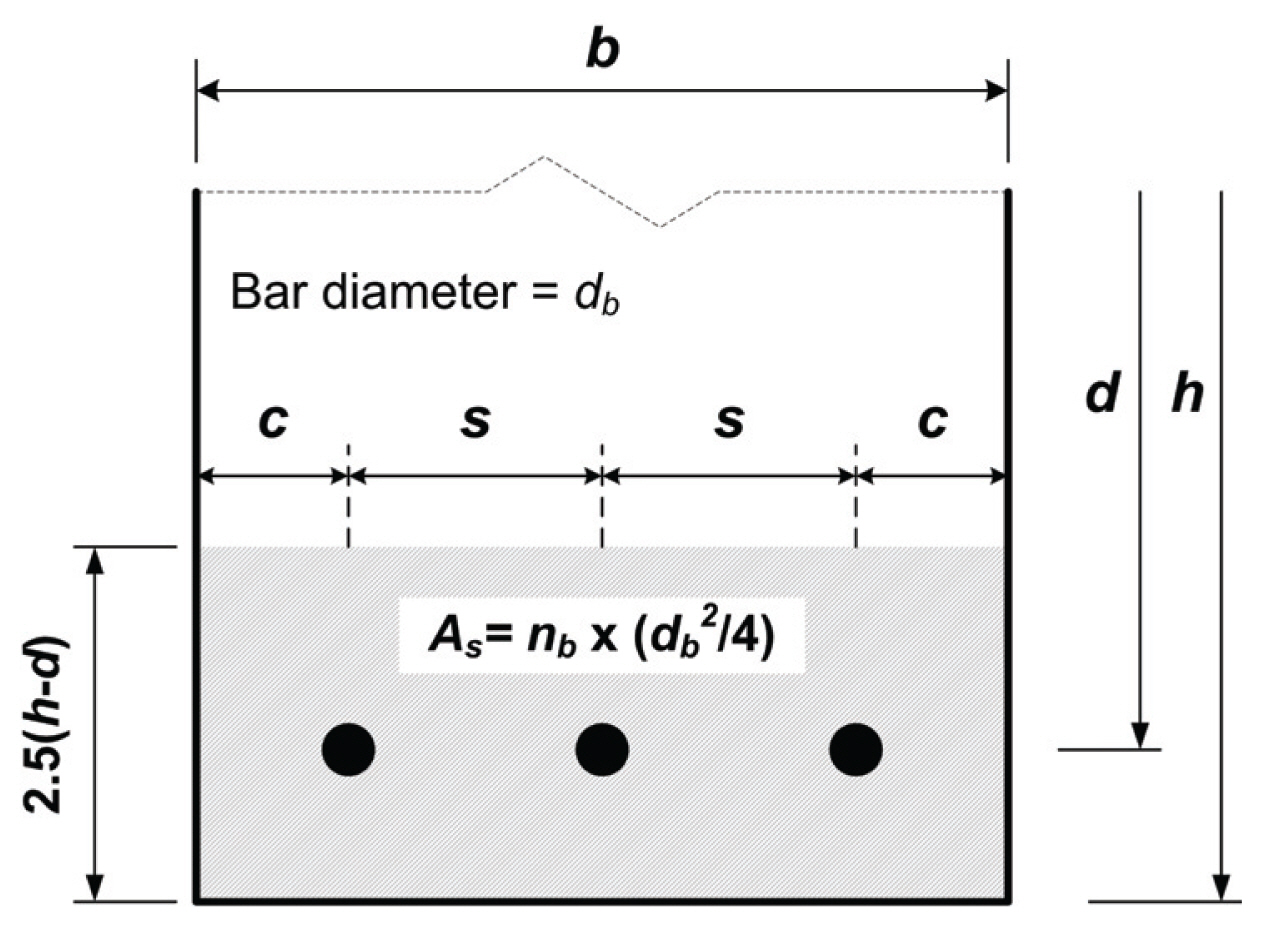
한편, 철근콘크리트 부재의 균열거동과 관련된 평가를 위해서는 앞 절에서 설명한 바와 같이 인장 현재를 기준으로 하는 유효인장단면적을 이용한다. 그런데, 이 연구에서 제안하는 최대철근간격에 대한 규정은 철근콘크리트 부재의 성능 진단이나 사용성 평가에 직접 적용이 되므로, 유효인장단면적이 아닌 기하적인 전체 단면적으로 고려를 해야 한다. 따라서, Fig. 3(a)에 보인 것과 같은 보를 기준으로 Fig. 5에 도해한 것과 같이 인장철근의 간격 s를 기준으로 단면 폭 b에 대해서 배치된 철근의 개수 nb와 간격 s의 곱으로 정의한다.
그리고, Fig. 5에서 측면 피복두께 c는 철근콘크리트 보에 적용하는 철근의 수평 순간격과 피복두께에 대한 설계기준의 규정 및 일반적인 보 설계조건을 고려하고, Choi and Kim (2011)의 연구를 참고로 하여 인장철근 간격 s의 1/2로 가정하였다.
이와 함께, Eq. (10)의 유효 인장철근비 ρe는 전체 단면적을 고려할 수 있는 기하적 철근비 ρ로 변형을 해야 하는데, KCI-12, KHBDC 및 EC 2에서 모두 동일하게 규정하고 있는 Fig. 3(a)에 보인 보의 유효 인장단면적을 이용하여 두 철근비간의 관계를 다음과 같이 정의하고,
Eq. (12)로부터 유효 인장철근비 ρe를 다음과 같이 정의한다.
따라서, 기하적 철근비를 반영할 수 있도록 수정된 유효 인장철근비 ρe를 Eq. (10)에 대입하여 다시 정리하면 다음과 같다.
Eq. (15)를 이용하여 철근간격 s를 유도할 수 있도록 철근지름 db항으로 다음과 같이 정리한 후,
4. 최대 철근간격 제안
4.1 최대 철근간격 산정
이상과 같이 유도된 철근간격 식을 이용하면, 사용하중 구간에 해당하는 철근응력 단계별로 철근콘크리트 보의 단면 깊이에 상관없는 간접 균열제어를 위한 최대 철근간격을 얻을 수 있다.
이를 위하여 Fig. 4 및 앞 절에서 설명한 것과 같이 철근콘크리트 보의 간접 균열제어를 위한 최대 철근간격 및 최대 철근지름을 산정하기 위해 적용한 한계 허용 균열폭에 대해서 KHBDC에서 규정하고 있는 wk = 0.3mm를 적용하였다. 그리고, 콘크리트 인장강도 fct는 Euro-Design Handbook에서 적용한 2.5 MPa에 해당하는 콘크리트 압축강도가 27 MPa이므로, KHBDC에서 규정하는 콘크리트 인장강도 식으로 다시 환산하여 계산한 2.9 MPa을 적용하였다. 콘크리트 인장강도를 KHBDC의 규정에 의한 값으로 재환산한 이유는 국내에서 생산되는 콘크리트의 특성을 반영할 수 있도록 하기 위함이며, 사용성능 평가 및 설계 실무에 직접 적용할 수 있는 설계기준이 KHBDC 뿐이기 때문이다. 이와 함께 피복두께는 40 mm, 철근 탄성계수 Es는 2×105 MPa, 탄성계수비 n은 8을 Eq. (17)에 적용하였다.
이 값들을 적용하여 설계 실무에서 적용하는 철근비인 2% 범위내에서 단면깊이 h를 400 mm에서 800 mm까지 100 mm씩 변화시켜가면서 철근간격을 계산하고, 사용하중 구간에 해당한다고 간주할 수 있으며 KHBDC의 규정과 같은 160∼360 MPa의 철근응력을 40 MPa 단계별로 Fig. 6에 도해하였다.
Fig. 6에 도해한 철근응력 단계별 최대 철근간격 계산 결과에 따르면, Fig. 4에 보인 것과 같은Euro-Design Handbook이나 KHBDC와 다르게 단면 깊이 h의 변화에 상관없이 일정한 값에 수렴하는 것을 확인할 수 있다. 또한, 철근응력이 증가할수록 최대 철근간격은 감소하는 것으로 나타났으며, 이러한 결과는 Table 1에 정리한 KHBDC의 규정과 동일한 경향을 나타내는 것이라고 할 수 있다.
한편, 간접 균열제어를 위한 최대 철근간격과 최대 철근지름은 휨부재 설계의 안전성 확보를 위하여 최소 철근비 규정을 만족하여야 한다. 철근콘크리트 보에 사용되는 철근의 항복강도를 300∼500 MPa로 간주한다면, KHBDC에서 규정하는 최소철근비를 적용하였을 때 0.23∼0.47% 범위에 있으므로 이 연구에서는 이들 값의 평균인 0.35%를 최대 철근간격 산정을 위한 최소값으로 정하였다.
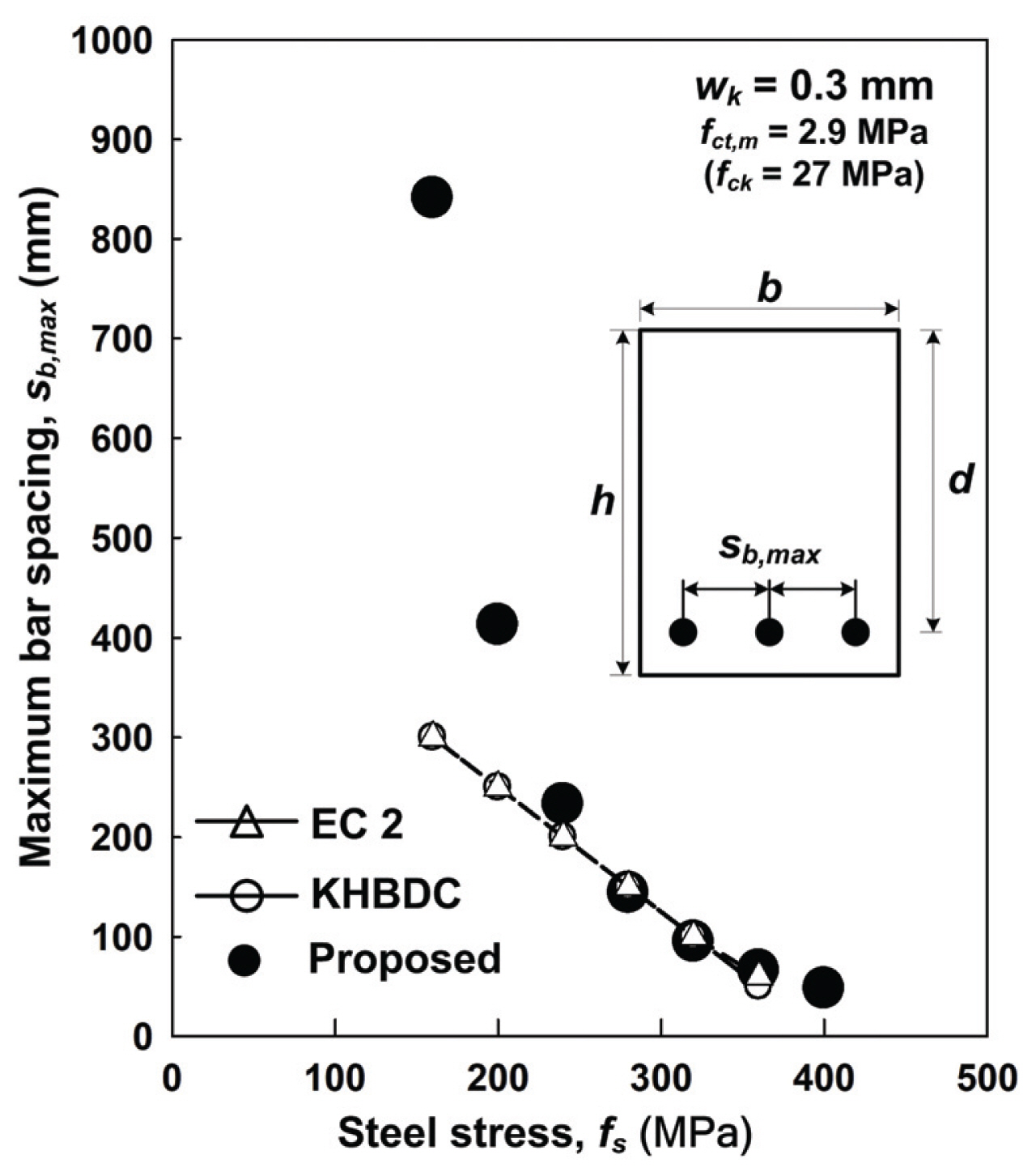
이상과 같은 분석결과를 바탕으로 이 연구에서는 철근콘크리트 보의 간접 균열제어를 위한 최대 철근간격을 철근응력 수준별로 산정하여 제안하고, 이 값들을 KHBDC와 동일한 조건으로 하여 Table 3에 정리하였으며, KHBDC에서 규정하는 값들과 비교하여 Fig. 7에 도해하였다.
이에 따르면 철근응력이 낮은 200 MPa 이하에서는 KHBDC의 값과 비교하여 40% 이상의 큰 차이가 발생하고, 상대적으로 높은 응력 단계인 360 MPa 에서는 약 25% 정도의 차이가 발생한다. 그러나, 철근콘크리트 휨부재의 사용한계상태 또는 사용성능 검증이 필요한 철근응력 단계는 일반적으로 철근 항복강도 fy의 2/3 수준을 기준으로 한다(Frosch, 1999; Choi and Kim, 2011). 따라서 철근콘크리트 휨부재에 사용하는 철근의 항복강도 fy가 400, 500 MPa이라고 하면, 사용하중 수준에 해당하는 철근의 응력은 각각 267, 333 MPa이 되므로, 이 응력 단계를 포함하는 240∼360 MPa 범위에서는 대체적으로 KHBDC와 유사한 결과를 나타낸다고 할 수 있다.
4.2 콘크리트 압축강도 보정
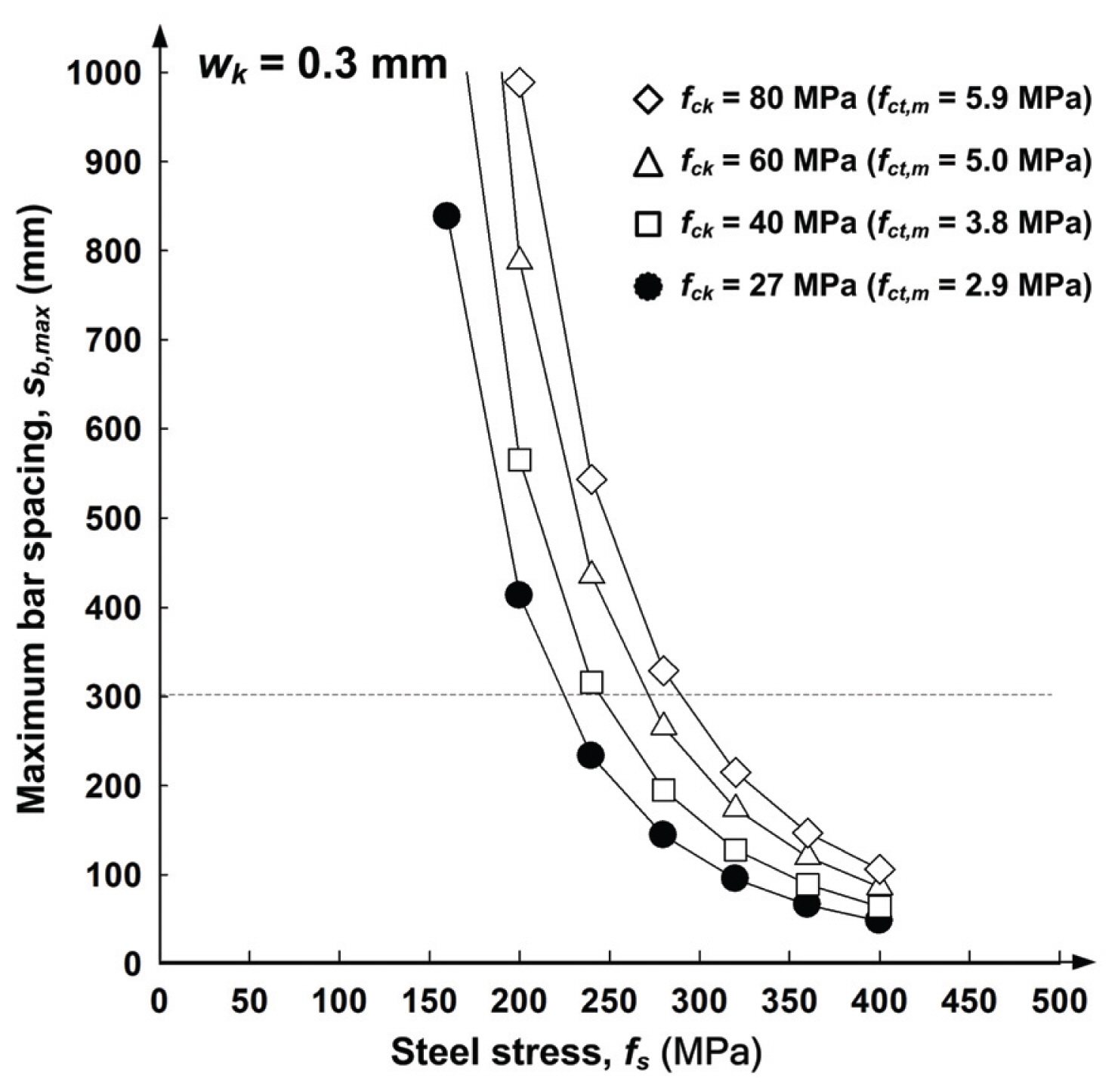
철근콘크리트 보의 간접 균열제어를 위하여 이 연구에서 제안하는 최대 철근간격은 KHBDC에서 도입할 필요성이 있는 EC 2의 보정계수들을 표현한 Eq. (6) 중 단면깊이에 대한 보정이 필요 없는 장점이 있다. 그러나, 앞 절에서 유도한 철근간격 산정을 위한 Eq. (17)은 콘크리트 압축강도가 27 MPa을 기준으로 유도가 되었으므로, 이 식을 이용하여 산정된 Table 3의 값들은 Fig. 8에 보인 것과 같이비교적 일정하게 증가하게 된다. 따라서, 콘크리트 압축강도가 증가함에 따라서 철근응력 단계별로 최대 철근간격의 변화를 적절히 반영할 수 있는 압축강도에 대한 보정은 필요하다고 하겠다.
이와 관련하여 KHBDC에서는 단면 깊이와 마찬가지로 별도의 보정계수를 규정하고 있지 않지만, EC 2에서는 Eq. (6)과 같이 콘크리트 인장강도 fct를 변수로 하는 콘크리트 압축강도에 따른 보정계수를 규정하고 있다.
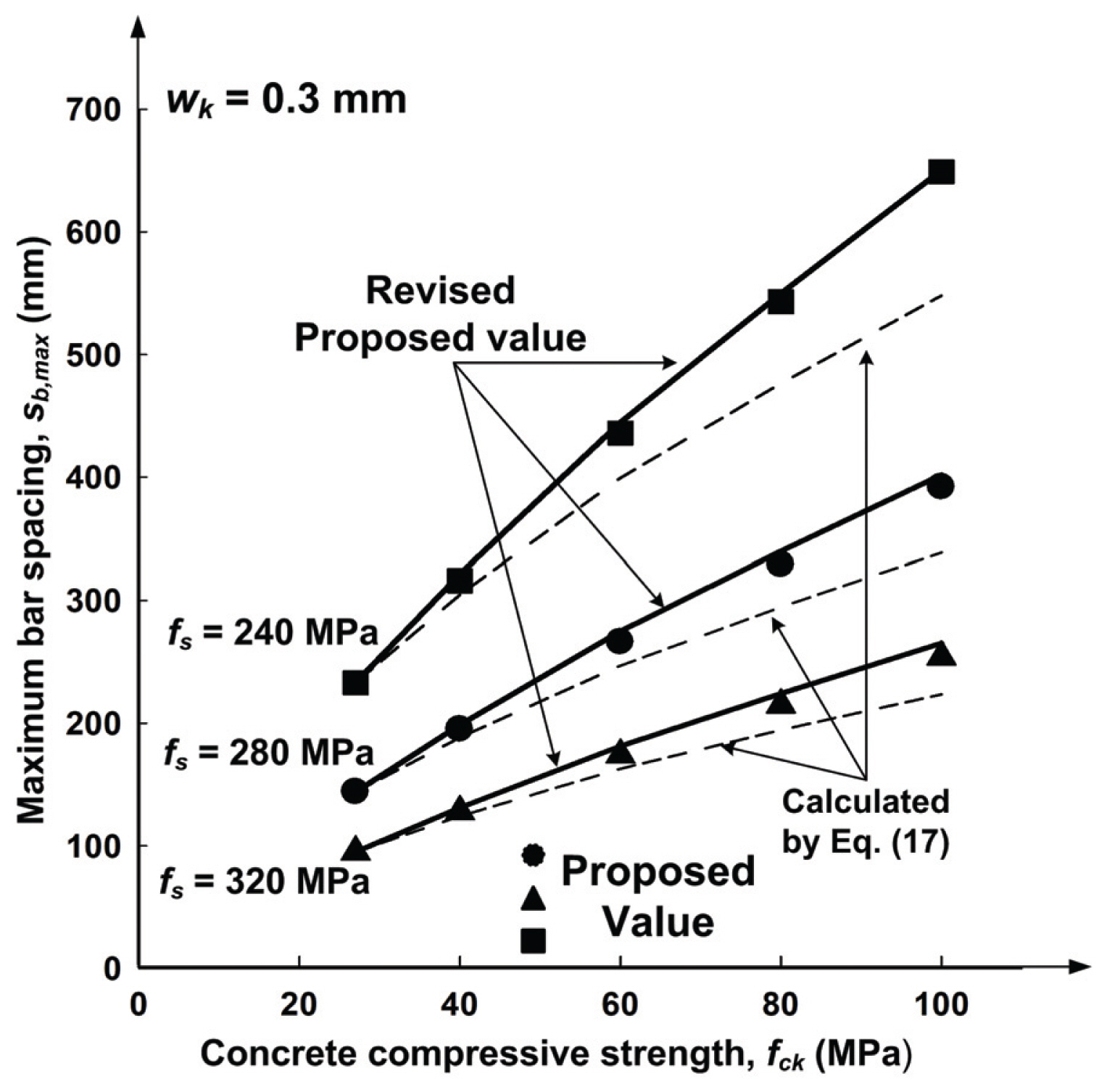
이 연구에서는 콘크리트 설계기준 압축강도 fck를 기준강도 27 MPa부터 40, 60, 80 MPa까지 반영하여 각 강도별 최대 철근간격을 계산한 후, 이 값들을 이용하여 KHBDC의 근간이 되는 EC 2에서 규정하는 보정계수와 동일한 형태를 갖도록 콘크리트 압축강도를 반영하는 항인 fct/2.9를 기본식으로 선정하였다. 그리고, 이 식에 콘크리트 압축강도의 영향을 반영할 수 있는 지수를 도입하여 이 값들을 압축강도별로 계산한 후, 사용하중 수준에 해당하는 철근 응력인 240∼320 MPa의 범위에 대해서 통계분석을 실시하여 다음과 같은 보정계수를 제안하였다.
5. 결 론
이 연구에서는 철근콘크리트 보의 사용성능 진단 및 평가와 관련하여 균열폭을 직접계산하지 않고도 사용성 검토를 할 수 있는 간접균열제어 방법의 일환으로 설계 균열폭 산정식을 이용하여 한계 균열폭 0.3 mm를 만족하도록 사용하중 구간의 철근 응력 수준에서 필요한 최대철근간격을 제안하였다. 이 값들은 철근비 0.35∼2.0%와 단면 깊이 400∼800 mm 범위 내에서 단면 깊이의 변화에 대한 보정이 필요 없도록 1차식 형태의 인장강화효과와 유효인장철근비와 철근지름만을 변수로 하는 균열간격을 이용하였다. 또한 콘크리트 압축강도 변화에 대한 정확한 보정이 될 수 있도록 콘크리트 강도 보정계수를 함께 제안하였다. 이상과 같은 연구결과에 따라 다음과 같은 결론을 얻었다.
(1) 현행 도로교설계기준(한계상태설계법)의 간접균열제어 규정 중 최대철근간격은 단면의 깊이에 따라서 기준값이 변화하므로 이에 대한 보정이 필요하다.
(2) 단면 깊이의 변화에 따른 별도의 보정계수가 필요 없도록 1차식 형태의 인장강화효과를 이용하여 사용하중 구간에 해당하는 철근의 응력 수준별 최대철근간격을 새롭게 제안하였다.
(3) 이와 함께 현행 도로교설계기준(한계상태설계법)의 최대철근간격 규정에서 반영하고 있지 않는 콘크리트 압축강도의 증가에 따른 변화를 반영할 수 있도록 Eurocode 2의 보정계수를 수정하여 제안하였다.