혼합분포형을 이용한 한국의 연최대 풍속 분석
Frequency Analysis of Annual Maximum Wind Speed in Korea using Mixture Distribution
Article information
Abstract
최근 풍속자료의 빈도해석 연구에서 풍속자료의 분포형으로 혼합확률분포이 적합하다는 결과가 보고되고 있다. 연 최대 풍속자료는 풍속자료 중에서 연 최대 값을 뽑아 낸 자료로, 풍속자료의 특성에 따라 연 최대 풍속자료의 특성이 결정될 가능성이 높다. 그래서, 본 연구에서는 국내 연 최대 풍속자료에 대한 혼합분포형의 적합성을 평가였다. 혼합분포형으로는 Gumbel 분포형을 두 개를 합성한 분포형을 사용하였고, 혼합분포형의 매개변수를 추정하기 위해서, expectation-maximization 알고리즘을 적용하였다. 추정된 혼합분포형은 다양한 적합도 평가 기준을 토대로 Gumbel, Weibul, Generalized Extreme Value, Kappa 분포형과 국내 풍속자료에 대한 적합도를 비교하였다. 평가결과, 혼합분포형이 극치 분석에 사용되는 분포형들보다 국내 연 최대 풍속자료에 적합한 것으로 나타났고, 혼합분포모형이 최적분포형으로 선정되지 않은 지점에서도 높은 적합도를 보이는 것으로 확인하였다.
Trans Abstract
Recently, many studies on wind speed frequency analysis reported that mixture distribution is appropriate for the distribution of wind speed data. Since the annual maximum wind speed data are a subsample of wind speed data, the characteristics of the annual maximum wind speed data are highly likely related to those of wind speed data. Hence, in this study, the fit of mixture distribution for annual maximum wind speed data measured in Korea was assessed. A two-component Gumbel mixture distribution was employed, and an expectation-maximization algorithm was used as fitting method. The fit of the mixture distribution was compared with those of the Gumbel, Weibull, Generalized Extreme Value, and Kappa distributions, based on several goodness-of-fit measurements. The results show that the fit of the mixture distribution for the annual maximum wind speed in Korea was superior to the fits of other distributions. Additionally, the mixture distribution led to good fits also at those stations where it was not selected as the most appropriate distribution.
1. 서 론
극치 풍속자료의 빈도해석은 초고층건출물, 풍속발전기 등과 같은 다양한 구조물의 설계 기준으로 널리 사용되고 있다. 정확한 극치 풍속자료의 빈도해석은 구조물의 안전성을 높이고, 과대설계를 막아 건설비용을 절약할 수 있다. 그러나 풍속자료는 다른 자연현상보다 높은 변동성과 지역성을 가지고 있는 변수로 적절한 통계분석 기법을 이용하여 정확한 빈도해석결과를 얻는 것이 매우 중요하다. 특히 우리나라는 극치 풍속자료들이 태풍으로 인하여 발생하고 산간지역이 많아 다른 나라와 비교하여 높은 공간 및 시간 변동성을 가지고 있다. 정확한 국내 극치 풍속자료의 빈도해석을 위하여 다양한 연구가 진행되었다.
Ha and Kim (2002)는 초고층건축물이나 관광타워용 탑상 구조물 살계를 위해 풍향과 풍속을 동시에 고려할 수 있는 풍향⋅풍속 결합 확률분포 모형을 활용하여 풍향별 재현기대풍속을 평가하였다. 이를 위해 전국 32개 지역 기상관측소의 10년간 연최대 풍속 발생 시의 풍향과 풍속 기록을 사용하였으며 이를 통해 우리나라에서 발생하는 짧은 재현기간에 해당하는 강풍의 풍향에 대한 전반적인 특성 및 지역별 특성을 살펴보고 풍향 발생빈도와 풍속의 세기 등을 분석하였다. Lee et al. (2010)은 우리나라의 주요 풍력발전 지역 15곳을 대상으로 풍력발전기 허브의 구조적 안정성을 확보하기 위해 국가바람지도를 활용한 극한풍속을 추청한 바 있다. 이를 위해서 2005년부터 2007년까지 3년간의 시계열 풍속으로부터 일최대 풍속과 월최대 풍속자료를 생성하였고, 이를 바탕으로 극치분석을 통한 극한풍속을 추정한 결과 월최대 풍속자료가 적합할 것으로 분석하였다. Shin et al. (2011)은 건축물 설계 시 풍하중을 산정하기 위해서 필요한 기본풍속을 위해 서울, 부산, 그리고 제주를 대상으로 1, 2, 3년 간의 일최대 풍속자료와 1970년부터 2009년까지의 40년간의 연최대 풍속자료를 활용하여 극치통계분석을 수행한 바 있다. Kim and Kim (2017)은 지형 및 지표면 조도를 고려한 기본풍속 산정 방안에 대한 연구를 진행하였다. 실제 내풍설계시 대상 지형에 맞게 풍속자료를 보정 및 외삽을 실시하여야 한다. Kim and Kim (2017)은 보정 및 외삽에 영향을 주는 지형 및 지표면 조도가 최대풍속분포에 주는 영향에 대하여 연구를 실시하였다. 보정 전후로 100년 재현기간의 연최대풍속의 경우 평균적으로 약 0.33 m/s 차이가 나는 것을 확인 하였다. Ha, Y.-C. (2018)은 건축물의 내풍설계시 반영되는 극한강도 풍하중을 산정하기 위하여 우리나라 기상관측소의 연최대 풍속자료를 활용하여 재현기간에 따른 기대풍속을 산정하고 한국형 강도설계용으로 기본풍속지도를 제시한바 있다.
일반적인 풍속자료의 빈도해석에서는 Weibull (WBL) 분포형이 널리 적용되고 있으나, 많은 지역에서 WBL 분포형으로는 적절한 빈도해석이 불가능한 것으로 나타났다(Ouarda et al., 2015). WBL 분포형의 한계성을 극복하고자 다양한 확률분포형을 이용한 풍속자료의 빈도해석을 실시하였으나, 현재는 혼합분포모형이 기존 확률분포형의 대안으로 널리 적용되고 있다.
Ouarda et al. (2015)은 아랍에미리트의 10분 평균 풍속자료의 최적분포형 선정에 대한 연구를 수행하였다. 연구 결과 WBL-WBL 혼합분포형이 최적분포형으로 선정되었다. Shin et al. (2016)은 Ouarda et al. (2015)에서 분석하지 못한 다양한 혼합분포모형의 아랍에미리트 10분 평균 풍속자료에 대한 적합도를 평가하였다. 평가결과, WBL-Gumbel (WBL-GUM) 분포형이 최적분포형으로 선정되었다. WBL-GUM 분포형은 다른 혼합분포형보다 높은 적합도를 보였다. 특히, 기존에 널리 사용되었던 WBL 분포형과 같은 비혼합분포형들보다 높은 적합도를 보이는 것으로 나타났다.
이러한 풍속자료의 혼합분포모형을 따르는 특성으로 인하여, 극치 풍속자료에 대해서도 혼합분포형의 적합성을 평가 할 필요가 있다. 극치 자료들의 빈도해석을 위해서도 많은 혼합분포모형이 적용되고 있다. Shin and Lee (2014)은 혼합분포모형을 위한 새로운 매개변수 추정방법을 제안하였으며, 제안된 방법의 성능을 평가하기 위해서, 극치 자료의 빈도해석에 제안된 방법을 적용하였다. 그 결과 혼합분포모형이 극치 빈도해석에 적용 가능한 것으로 나타났다. Shin et al. (2015)은 한국의 연최대 강우량 자료의 빈도해석에 동종 및 이종 혼합분포모형의 적합도를 평가하였다. Gamma 분포와 GUM 분포를 혼합한 Gamma-GUM 혼합분포형이 다른 비혼합분포형과 동종 혼합분포형보다 높은 적합도를 보이는 것으로 나타났다.
혼합분포모형을 이용하여 연최대 풍속자료의 빈도해석을 실시할 경우 높은 정확도의 결과를 얻을 수 있을 것으로 예상되어, 본 연구에서는 국내 연최대 풍속자료의 빈도해석에 대한 혼합분포모형의 적합도를 평가하였다. 적합도 평가를 위하여 다양한 적합도 평가 기준을 적용하였다. 적합도 비교를 위해 기존에 극치 풍속 빈도해석에서 사용된 확률분포형들과의 성능을 비교 분석하였다.
2. 이 론
2.1 확률분포모형
2.1.1 혼합분포모형
혼합분포모형은 한 개 이상의 확률분포형 모형의 가중합으로 구성되어있으며, 다음과 같이 정의할 수 있다.
θi는 각 분포형 모형의 매개변수이고, g는 혼합분포에 포함되어 있는 분포형의 수이고, πi는 각 분포형의 가중치이며, 가중치의 합은 1이고, 가중치는 양의 값을 가진다. 본 연구에서는 혼합분포모형으로 GUM 분포형 두 개를 합성한 혼합분포모형을 사용하였다. GUM 분포형은 2개의 매개변수를 가진 극치 확률분포형으로, 극한 풍속, 극한 강우, 홍수량과 같은 극치자료를 분석하는데 널리 사용되고 있다. 또한, GUM-GUM 혼합분포형은 극치자료의 빈도해석 많이 적용되고 있다(Shin et al., 2015). Generalized extreme value (GEV) 분포형도 극치자료 빈도해석에 널리 사용되고 있으나, GEV- GEV 혼합분포형의 경우 7개의 매개변수를 가지게 되어 가용 자료수에 비하여 많은 매개변수를 가진 것으로 생각되어 본 연구에는 5개의 매개변수를 가지는 GUM-GUM 혼합분포형을 적용하였다. GUM-GUM 혼합분포형의 확률밀도함수는 Eq. (3)과 같다.
2.1.2 기존의 확률분포모형
연최대 풍속자료의 빈도해석에 대한 혼합분포모형의 성능을 평가하기 위해서는, 기존에 사용된 확률분포모형들과 성능을 비교하는 것이 필요하다. 본 연구에서는 기존에 적용된 확률분포형으로 GUM, GEV, WBL, Kappa (KAP) 분포형을 사용하였다. WBL 분포형은 극치분포형은 아니나, 풍속자료를 분석하는데 널리 사용되기 때문에 적용하였다. KAP 분포형은 네 개의 매개변수를 가진 확률분포형으로 다른 확률분포형들 보다 다양한 극치자료 분석에 용이하다. 극치 빈도해석에서 널리 사용되는 GEV와 generalized pareto 분포형은 KAP 분포형의 특수한 형태로 KAP 분포형은 3변수 극치 분포형이 적절히 분석이 안되는 자료의 확률분포형으로 널리 사용되고 있다. Table 1은 기존에 사용되어온 확률분포형의 누적분포함수를 정리하여 놓은 표이다.
2.2 매개변수 추정방법
본 연구에서는 기존의 확률분포형의 매개변수를 추정하기 위하여, 최우도법(maximum likelihood method)을 적용하였다. KAP 분포형의 매개변수 추정방법으로는 L-moment법을 이용하였다(Hosking and Wallis, 2005). 혼합분포형의 경우 Expectation-Maximization 알고리즘을 적용하였다.
혼합분포는 다른 두 개 이상의 확률분포형이 가중 합으로 구성되어 일반적인 최우도법을 사용하여 매개변수를 추정하기에 문제가 어려움이 있다. Expectation-Maximization (EM) 알고리즘은 이런 최우도법의 문제점을 해결하고 혼합분포형의 매개변수를 추정하기 위하여 개발되었다(Dempster et al., 1977). EM 알고리즘은 완전한 관측값이 있다는 가정하에 혼합분포모형의 매개변수를 추정한다. EM 알고리즘은 추정(expectation)과 최대화(maximization)의 두 개의 단계로 구성되어 있다. 첫 번째 단계는 추정 단계로 각 관측값이 각 확률분포형 모형에서 알지 못하는 변수의 발생할 확률값을 추정한다. 두 번째 단계는 최대화 단계로 추정단계에서 추정 된 확률값을 이용하여 혼합분포모형 안에 각 확률분포형의 우도함수 값이 최대값이 되는 확률분포형의 매개변수를 찾는 다. 정해진 수렴기준을 만족하는 매개변수가 추정될 때까지 추정단계와 최대화 단계를 반복한다.
2.3 적합성 평가 지표
본 연구에서는 확률분포형의 적합성을 평가하기 위해서 Akaike Information Criterion (AIC), 평균제곱근오차(root mean square error, RMSE), 결정계수(R2), Kolmogorov-Smirnov (KS) 통계치를 사용하였다. AIC를 산정하는 공식은 Eq. (4)와 같다.
Femp(xi)는 경험적인 누적확률값으로 Cunnane, C. 도시위치공식을 이용하여 추정하였다(Cunnane, C., 1973).
3. 자 료
3.1 기상관측소 및 자료 정보
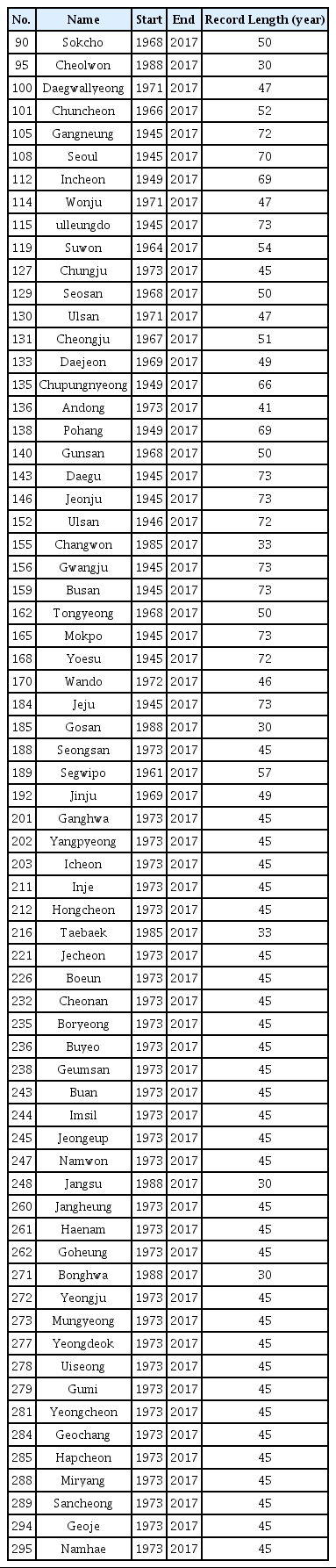
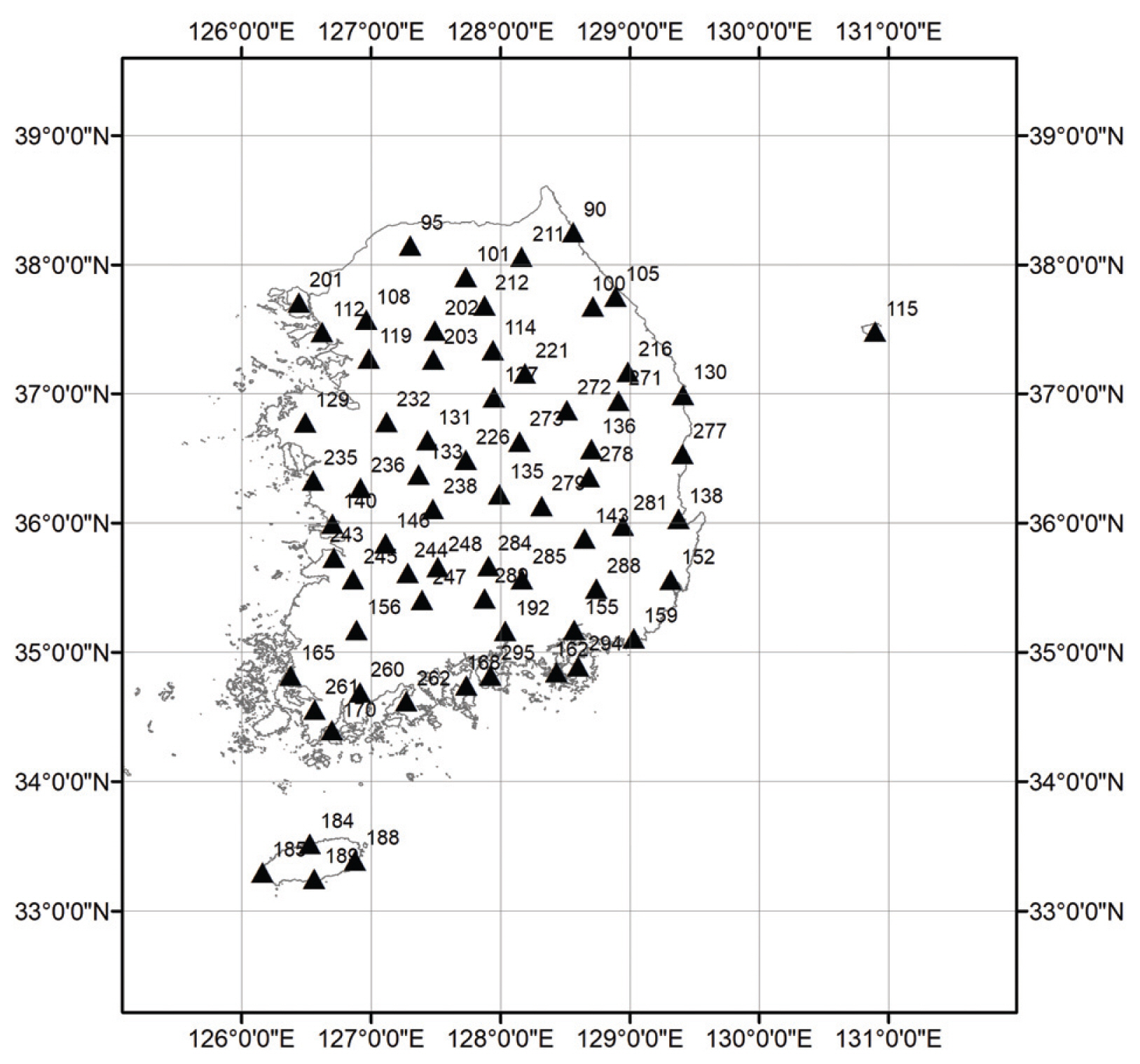
연 최대 풍속자료로는 매년 일 최대 풍속자료의 최대값을 사용하였다. 일 최대 풍속자료는 기상청 유인관측소 지점의 일 최대 풍속 관측자료를 사용하였다. 현재 기상청에서 94개 유인관측소를 운영하고 있으나, 본 연구에서는 30년 이상의 기록을 가지고 있는 67지점의 자료를 사용하였다. 67개 기상관측소의 정보는 Table 2에 나타나 있고, 기상관측소의 위치는 Fig. 1에 표시 되어 있다.
3.2 연 최대 풍속 자료 특성
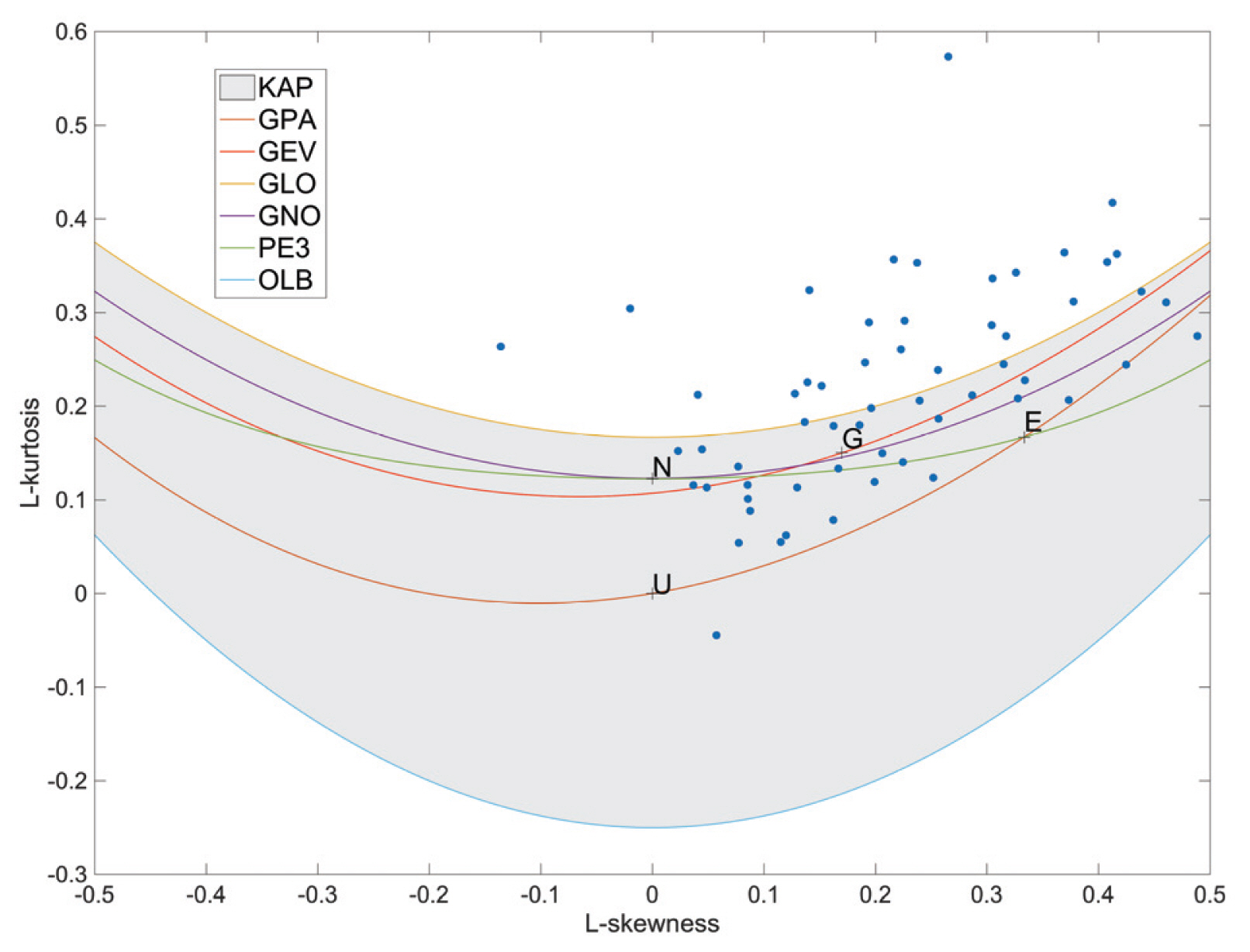
연 최대 풍속자료의 빈도해석을 실시하기 전에 국내 연 최대 풍속자료의 통계적인 특성을 분석하였다. 연 최대 풍속자료를 모의하기에 적합한 확률분포형은 도시적으로 확인해 보고자, 각 지점의 연 최대 풍속자료에 대해서 L-moment ratio diagram을 Fig. 2에 도시 하였다. L-moment ratio diagram은 관측 자료의 표본 L-moment ratio를 계산하고, 확률분포형의 이론적인 L-moment ratio와 도시적인 비교를 통하여 주어진 자료의 적합한 확률분포형을 도시적으로 판단하는 분석 방법이다(Hosking and Wallis, 2005). L-moment diagram을 보면 많은 지점의 연 최대 풍속자료가 회색범위 밖에 존재하는 것을 확인할 수 있다. 회색 범위는 Kappa분포형으로 적절히 재현이 가능한 자료의 범위를 나타낸다. 극치 빈도해석 널리 쓰이는 Gumbel과 GEV 분포형이 Kappa 분포형에 특수한 형태인 것으로 미루어 보아, 기존에 사용되어 오던 극치 확률분포형으로는 연최대 풍속자료를 적절히 모의가 안 되는 것으로 판단된다.
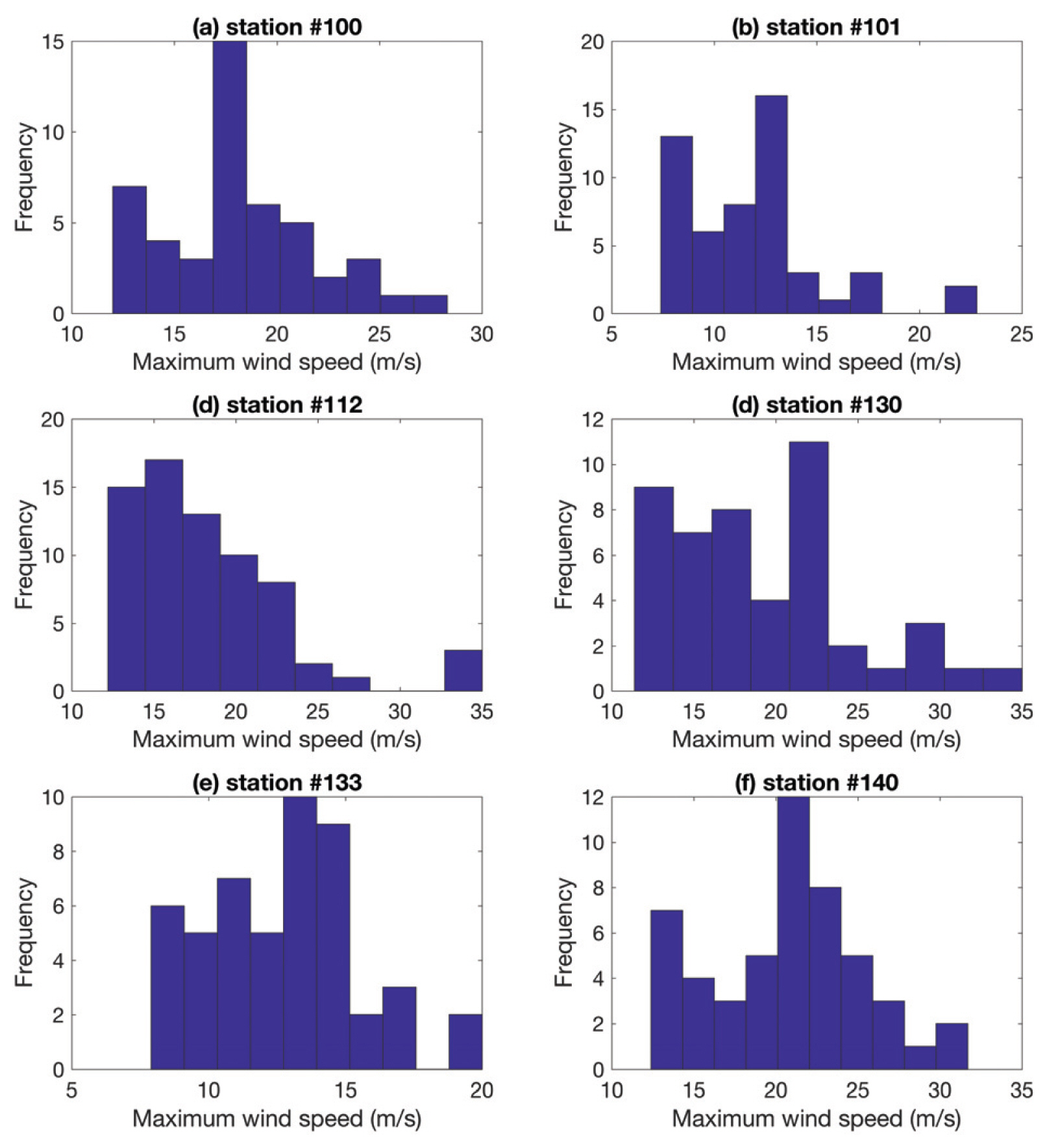
회색 범위 밖에 있는 자료들의 자세한 특성을 알아보고자 범위 밖에 있는 6개 지점의 히스토그램을 Fig. 3에 도시하였다. Fig. 3을 보면 일반적인 극치 확률분포형이 보이는 작은 값을 가지는 자료의 높은 빈도수가 보이지 않는 것을 확인 할 수 있다. 대부분의 최빈도를 보이는 값이 전체 풍속자료 범위에서 중간에 위치하거나, 여러곳으로 나누어져 있는 것을 확인 할 수 있다. 춘천(101)지점과 군산(140)지점의 히스토그램을 보면 두 개의 봉우리가 존재하는 것을 확인 할 수 있다. 이런 두 개의 봉우리를 보이는 것은 혼합분포형의 가장 큰 특징으로 국내의 많은 지점의 연 최대 풍속자료의 확률분포형이 혼합분포형을 따를 것으로 추정된다.
4. 결과 분석
4.1 적합도 결과
국내 연 최대 풍속자료에 대해서 GUM-GUM 혼합분포형의 적합도를 평가하기 위해, AIC, RMSE, 결정계수, KS 통계치를 적합도 평가기준을 이용하여 기존에 사용되어 온 확률분포형들과의 적합도를 비교하였다.
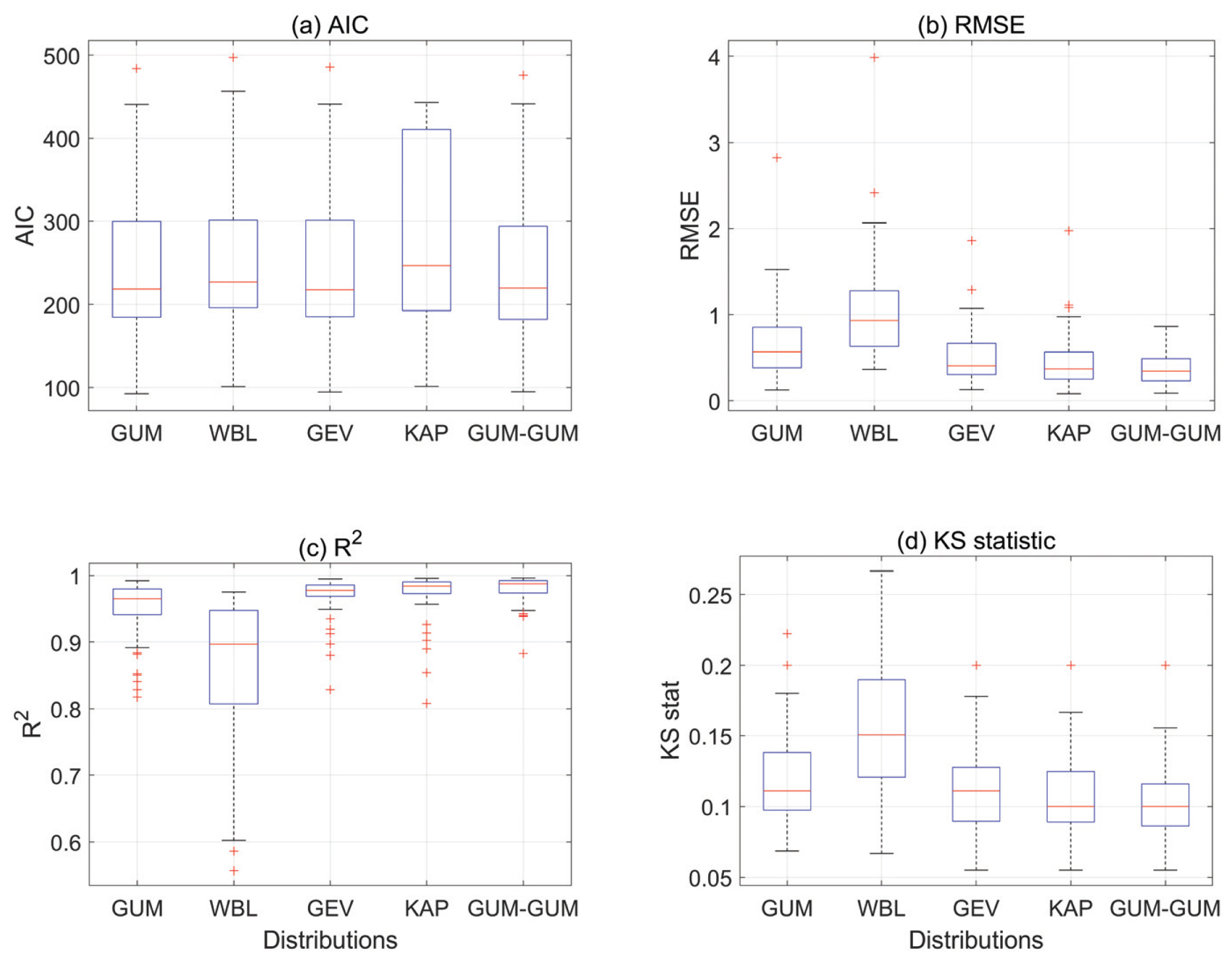
국내 전체 기상관측소에 대한 각 확률분포형의 적합도를 비교하고자, 각 적합도 평가지수별로 boxplot를 Fig. 4에 도시하였다. AIC를 기준으로는 Gumbel (GUM)과 GUM-GUM 분포형이 전체적으로 낮은 AIC를 보였다. AIC는 모형내의 매개변수 개수를 고려하는 항이 포함하고 있다. 이러한 이유로 GUM 분포형이 GEV나 Kappa 분포형보다 낮은 AIC값을 가지는 것으로 보인다. GUM-GUM 분포형의 매개변수 개수는 5개로 적용된 확률분포형 중에서는 가장 많은 수의 매개변수를 가지고 있다. GUM-GUM 분포형이 많은 매개변수를 가지고 있음에도 낮은 AIC 값을 가지는 것을 보면, GUM-GUM 분포형이 연 최대 풍속 자료를 모의하기에 매우 적합한 것을 확인할 수 있다. RMSE, 결정계수, KS 통계치를 기준으로는 Kappa와 GUM-GUM 분포형이 높은 적합성을 보이는 것을 확인할 수 있다. RMSE와 결정계수는 각 확률분포형의 확률풍속량이 관측 확률풍속량과 얼마나 비슷한지를 평가하는 지수로, Kappa와 GUM-GUM 분포형이 풍속확률량을 가장 적절히 모의하는 것으로 나타났다.
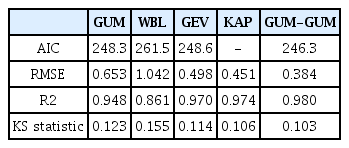
Table 3은 각 확률분포형에 대한 각 적합도 평가 지수의 평균값을 정리한 표이다. Kappa 분포형의 경우 하한 한계치가 있기 때문에, 몇몇 지점에 대해서는 AIC 값을 산정할 수 가 없었다. 이러한 이유로 Table 3에 Kappa 분포형의 AIC 평균값을 표기 하지 않았다. 모든 지수에서 GUM-GUM 분포형이 가장 높은 적합도를 보이는 것을 확인 할 수 있다. AIC를 기준으로는 GUM이 GUM-GUM 분포형 다음으로 좋은 값을 보였다. RMSE를 기준으로는 Weibull 분포형이 가장 높은 RMSE를 보였고, GUM-GUM 분포형이 가장 낮은 RMSE를 보였다. 결정계수와 KS 통계치는 RMSE와 비슷한 결과가 나타난 것을 확인 할 수 있었다. Weibull 분포형은 풍속자료를 분석하는데 가장 널리 쓰이고 있으나, 연최대 풍속자료를 분석하기에는 적절하지 않은 것으로 나타났다. Weibull 분포형을 제외한 다른 분포형들의 경우, 극치분포형들로 극치자료를 분석하기 위해 개발된 분포형들이기 때문에, 연최대 풍속자료에 대해서 Weibull 분포형보다 월등히 높은 적합도를 보이는 것을 확인 할 수 있었다.
자료에 대한 최적분포형을 선정하기 위해서는 적합도 평가 기준들의 전체 지점에 대한 분포나 평균값을 사용할 수 있으나, 지점별로 자료의 특성이 다를 경우 평균적으로 가장 적합한 분포형이 적절하지 않을 경우가 있다. 연 최대 풍속자료의 지점별 분포형적인 특성을 알아보고자, 지점별로 가장 적합하다고 선택된 분포형을 정리하였다. Table 4는 각 적합도 평가 기준에 따른 최적분포형으로 선택된 숫자료를 정리해 놓은 표이다. AIC를 기준으로는 GUM-GUM 분포형이 35개 지점에서 최적분포형으로 선택되었고, GUM 분포형이 23개 지점, GEV 분포형이 6개 지점, Kappa 분포형이 3개 지점에서 선택되었다.
AIC는 모형의 매개변수 개수를 평가할 때 고려하기 때문에, GUM분포형이 GUM-GUM 분포형 다음으로 많이 선택된 것 같다. GUM-GUM 분포형은 가장 많은 매개변수 개수를 가지고 있는 모형임에도 불구하고 가장 많은 지점에서 최적분포형으로 선택되었다. 매개변수 개수가 4개인 Kappa 분포형은 단 3개 지점에서만 최적분포형으로 선택되었다. 연 최대 풍속자료의 분포가 일반적인 단일 봉우리 형태를 가지고 있다면, AIC를 기준으로 하였을 때 GUM-GUM 분포형보다 매개변수 개수가 적은 Kappa분포형이 보다 많은 지점에서 선택되어 한다. Kappa 분포형이 아닌 GUM-GUM 분포형이 많은 지점에서 최적분포형으로 선택된 것은 많은 지점의 연 최대 풍속자료의 분포가 혼합분포형태를 갖는 다는 것을 의미한다. RMSE와 결정계수를 기준으로는 GUM-GUM 분포형과 Kappa 분포형이 비슷한 숫자로 최적분포형으로 선택되었다. GUM 분포형은 1개 지점에서 최적분포형으로 선택되었다. 37개 지점에 대해서는 비혼합분포가 최적분포형으로 선택되었고, 30개 지점에서는 혼합분포형이 최적분포형으로 선택되었다.
모든 적합도 평가 기준의 결과를 종합해 보면 GUM-GUM 분포형이 국내 연 최대 풍속자료에 대해서 가장 높은 적합도를 보이는 것을 확인 할 수 있었다. 물론, GUM-GUM 분포형이 모든 지점에서 최적분포형은 아니였으나, 전체적인 적합도 평가 기준과, 최적분포형으로 선택된 지점의 수로 보았을 때, GUM-GUM 분포형을 이용하여 연 최대 풍속자료를 분석하는 것이 적절한 것으로 판단된다.
GUM-GUM 분포형은 두 GUM 분포형을 결합한 분포형으로 한 분포형에서 상이한 통계학적인 특성을 가지는 한 분포형으로 표현할 수 있는 장점이 있다. 일반적으로 저풍속 구간을 대표하는 GUM분포형과 고풍속 구간을 대표하는 GUM분포형으로 나누어진다. 저풍속 구간의 최대풍속과 고풍속 구간의 최대풍속의 통계적인 특성이 같을 경우 GUM-GUM 분포형은 GEV나 GUM분포형과 같은 성능을 보인다. Table 4를 보면 GUM-GUM 분포형이 AIC를 기준으로 35개 지점에서 가장 적합한 분포형으로 판단되었다. 즉, 35개 지점의 최대풍속자료는 두 구간에 대하여 상이한 통계적 특성을 가지고 있는 것으로 판단된다.
4.2 확률최대풍속 비교
연 최대 풍속 빈도해석의 목적은 정확한 확률최대풍속을 추정하는데 있다. 확률최대풍속의 참값을 알 수 없기 때문에, 도시위치공식을 이용한 경험적인 확률최대풍속과 확률분포형을 통하여 산정된 확률최대풍속의 비교하여 대략적인 정확도를 평가 할 수 있다. 6개 지점의 경험적인 확률최대풍속과 확률분포형을 통하여 산정된 확률최대풍속을 Fig. 5에 도시하여 놓았다. 도시된 지점들은 GUM-GUM 분포형이 최적분포형으로 선택된 지점들이다.

Quantiles Plots of Observations, Gumbel, GEV, Kappa, Gum-Gum mixture distribution for stations Gangneung (105), Gunsan (140), Boeun (226), Jeongeup (245), Jangsu (248), and Bonghwa (271)
Fig. 5를 보면 GUM-GUM 분포형이 다른 분포형들 보다 경험적인 확률최대풍속과 가장 가까운 값을 보여주는 것을 확인 할 수 있다. 105, 226, 245, 248번 지점의 경우 높은 재현기간에서 GUM-GUM 분포형으로부터 산정된 확률최대풍속이 경험적인 확률최대풍속과 가장 흡사한 것으로 나타났다. 다른 분포형들의 경우 실제 값보다 낮은 값을 산정하거나, 매우 높은 값을 산정하는 것을 확인 할 수 있었다. 특히 GUM-GUM 분포형은 낮은 재현기간의 확률최대풍속에 대해서도 다른 분포형들보다 높은 정확도를 보이는 것으로 나타났다.
140과 271번 지점의 경우 높은 재현기간에 대하여 다른 분포형들이 과대추정하는 것을 확인 할 수 있으나, GUM-GUM 분포형의 경우 경험적인 확률최대풍속과 비슷한 값을 산정하는 것을 확인 할 수 있었다. GUM-GUM 분포형은 지점에 대하여 낮은 재현기간을 가지는 확률최대풍속에 대하여 정확도가 다른 분포형들보다 월등히 높은 것을 확인 할 수 있다. 140번 지점의 경우 재현기간이 2년 미만에 자료에 대하여 다른 분포형들보다 높은 정확도를 보였고, 271번 지점에 대해서는 재현기간 2년에서 10년 사이인 확률최대풍속에 대하여 높은 정확도를 보였다.
도시적인 해석을 통한 GUM-GUM 분포형의 적합도를 분석해 보았을 때에도, GUM-GUM 분포형이 다른 분포형보다 연 최대 풍속자료를 분석하기에 적합한 분포형으로 판단된다. 본 논문에서는 도시하지 않았지만, GUM-GUM 분포형이 최적분포형으로 선정되지 않은 지점에서는 GUM-GUM 분포형이 Kappa와 GEV 분포형과 비슷한 확률최대풍속를 산정하는 것을 확인하였다. 이런 지점들에 대해서는 GUMGUM 분포형이 다른 분포형들보다 매개변수 개수가 많기 때문에 Kappa나 GEV 분포형이 적절한 확률분포형으로 판단되나, GUM-GUM 분포형이 Kappa나 GEV 분포형과의 정확도 차이가 크지 않기 때문에 빈도해석의 편의성을 높이기 위해서는 GUM-GUM 분포형을 통일해서 사용하여도 무방할 것으로 판단된다.
5. 결 론
전체적인 적합도 평가 기준들의 결과와 도시적인 해석결과를 종합해 보면, GUM-GUM 분포형이 가장 높은 적합도를 보이는 것을 확인 할 수 있었다. 두 번째로 높은 적합도를 보인 것은 KAP 분포형인 것을 확인할 수 있었다. 확률분포형의 매개변수 개수를 고려한 적합도 평가 기준인 AIC에서도 GUM-GUM 분포형이 가장 높은 적합도를 보이는 것으로 나타났다. AIC를 기준으로는 GUM 분포형이 두 번째로 적합한 분포으로 나타났다. 또한, GUM-GUM 분포형을 이용하여 연최대 풍속자료의 빈도해석을 실시할 경우, 기존 분포형에서 나타나는 과대 및 과소 추정이 적게 일어나는 것을 확인하였다. 과대추정의 경우 설계구조물의 과대설계를 유발시켜 건설비용을 증가시키는 문제가 있다. 과소추정의 경우 구조물의 안전성에 문제를 야기 시킬 수 있다. GUM-GUM 분포형을 이용할 경우 다른 분포형 보다 이런 문제가 적게 발생할 것으로 판단된다.
연최대 풍속자료의 빈도해석에서 GUM-GUM 분포형을 사용하는 것이 적절한 것으로 판단되었다. GUM-GUM 분포형이 전체적으로는 가장 적합한 분포형으로 선택되었으나, 개별 지점을 대상으로 높은 정확도의 연최대 풍속자료의 빈도해석 결과가 필요할 경우, 다양한 분포형을 검토하여, 최적분포형을 선정하는 것이 필요할 것으로 판단된다. 극한푹속 추정시 주변지형에 따른 노풍도를 산정하여야 하고 기본풍속 산출고도로 외삽보정을 실시하여야 합니다. 후속 연구로는 이러한 외부 요인과 최대풍속의 확률분포간의 관계에 대한 연구가 진행되면 좋을 것으로 판단된다.
Acknowledgements
본 연구는 행정안전부 극한 재난대응 기반기술개발사업 의 연구비 지원(2017-MOIS31-001)에 의해 수행되었습니다.