|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(7); 2018 > Article |
|
Abstract
Although corrugated steel plate structures have largely been applied in Korea as well as globally due to their structural efficiency, the causes of damage occurring at bolted connections should be examined. In this study, detailed finite element models for a bolted connection were formed, and the stress distribution around the connection was evaluated for various parameters, such as the number and arrangement of bolts, loads, edge length, and the spacing of bolts, by considering the cross-sectional forces of actual structures. As a consequence of the analyses, the cracks observed at the plate near a bolt hole can be attributed to very high local stresses that occur at the contact surface between the bolt head or nut and the curved plate when fastening the bolt. When the cross-sectional forces induced by external loads are applied to these local stresses, stresses in excess of the yield strength can occur. Furthermore, larger stresses occurred in an incorrect joint lap than those occurring in a correct joint lap, regardless of the number of bolts, when subjected to a bending moment. In regard to the edge length and spacing of bolts, the current specifications are appropriate in terms of the stress level. Several countermeasures to reduce the local stress around a bolt hole during fastening were also discussed, such as the use of the washers with a curved surface. It is expected that this study can contribute to the extended use of corrugated steel plate structures by clarifying the causes of damage and proposing possible improvements.
мҡ”м§Җ
нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҖ кө¬мЎ°м Ғмқё нҡЁмңЁм„ұмңјлЎң мқён•ҳм—¬ көӯлӮҙмҷём—җм„ң нҷңл°ңнһҲ м Ғмҡ©лҗҳм–ҙ мҷ”мңјлӮҳ, ліјнҠё мқҙмқҢл¶Җмқҳ мҶҗмғҒ мӮ¬лЎҖм—җ лҢҖн•ң мӣҗмқё к·ңлӘ…мқҙ н•„мҡ”н•ң мӢӨм •мқҙлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” ліјнҠё мқҙмқҢл¶Җмқҳ мғҒм„ён•ң мң н•ңмҡ”мҶҢ лӘЁлҚёмқ„ кө¬м„ұн•ҳкі мӢӨкө¬мЎ°л¬јмқҳ лӢЁл©ҙл Ҙмқ„ кі л Өн•ҳм—¬ ліјнҠё к°ңмҲҳ, ліјнҠё л°°м—ҙ, н•ҳмӨ‘, м—°лӢЁкұ°лҰ¬, ліјнҠё к°„кІ©кіј к°ҷмқҖ лӢӨм–‘н•ң ліҖмҲҳм—җ лҢҖн•ҳм—¬ мқҙмқҢл¶Җм—җм„ң л°ңмғқн•ҳлҠ” мқ‘л Ҙ мғҒнғңлҘј мҳҲмёЎн•ҙ ліҙм•ҳлӢӨ. к·ё кІ°кіј ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗмқҳ к· м—ҙмқҖ мқҙлҜё ліјнҠё мІҙкІ° лӢЁкі„м—җм„ң ліјнҠё лЁёлҰ¬ лҳҗлҠ” л„ҲнҠёмҷҖ кіЎл©ҙ нҳ•мғҒмқҳ к°•нҢҗмқҙ м ‘мҙүн•ҳлҠ” л¶Җмң„м—җм„ң л°ңмғқн•ң нҒ° көӯл¶Җ мқ‘л Ҙ л•Ңл¬ёмңјлЎң нҢҗлӢЁлҗңлӢӨ. мқҙлҹ¬н•ң көӯл¶Җ мқ‘л Ҙм—җ мҷёл¶Җн•ҳмӨ‘м—җ мқҳн•ң лӢЁл©ҙл Ҙмқҙ лҚ”н•ҙм§Ҳ кІҪмҡ° к°•нҢҗ н•ӯліөк°•лҸ„ мқҙмғҒмқҳ мқ‘л ҘлҸ„ л°ңмғқн• мҲҳ мһҲлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ. лҳҗн•ң нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н• л•Ңм—җлҠ” ліјнҠё к°ңмҲҳм—җ кҙҖкі„ м—Ҷмқҙ м •л°°м—ҙліҙлӢӨ л¶Җл°°м—ҙлҗң ліјнҠём—җм„ң лҚ” нҒ° мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖлӢӨ. ліјнҠё мқҙмқҢл¶Җ м—°лӢЁкұ°лҰ¬ л°Ҹ ліјнҠё к°„кІ©мқҳ кІҪмҡ° мқ‘л Ҙ мҲҳмӨҖмңјлЎң нҢҗлӢЁн• л•Ң нҳ„н–ү к·ңм •мқҖ м Ғм Ҳн•ң кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ. н•ңнҺё кіЎл©ҙ мҷҖм…” мӮ¬мҡ© л“ұ ліјнҠё мІҙкІ° мӢңмқҳ көӯл¶Җ мқ‘л Ҙмқ„ м Җк°җн• мҲҳ мһҲлҠ” л°©м•Ҳм—җ лҢҖн•ҙм„ңлҸ„ л…јмқҳн•ҳмҳҖлӢӨ. мқҙ м—°кө¬лҠ” нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҳ мҶҗмғҒ мӣҗмқёмқ„ к·ңлӘ…н•ҳкі к°ңм„ л°©м•Ҳмқ„ м ңм•Ҳн•ЁмңјлЎңмҚЁ к·ё м Ғмҡ©мқҙ нҷ•лҢҖлҗҳлҠ”лҚ° кё°м—¬н• мҲҳ мһҲмқ„ кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ.
нҢҢнҳ•к°•нҢҗ(corrugated steel plate)мқҖ к°•нҢҗмқ„ м •н•ҙ진 к·ңкІ©мқҳ мЈјлҰ„мқ„ к°–лҸ„лЎқ м„ұнҳ•н•ҳм—¬ к°•м„ұмқ„ мҰқк°ҖмӢңнӮЁ кІғмңјлЎңм„ң, м§ҖмӨ‘кө¬мЎ°л¬јлЎң мӮ¬мҡ©лҗ кІҪмҡ° м„ёк·ёлЁјнҠё лӢЁмң„лЎң м ңмһ‘лҗҳм–ҙ нҳ„мһҘм—җм„ң мқҙмқҢл¶ҖлҘј ліјнҠёлЎң мІҙкІ°н•ң нӣ„ м–‘м§Ҳмқҳ нқҷмңјлЎң л’Өмұ„мӣҖн•ҳкІҢ лҗңлӢӨ. мқҙл•Ң мҷёл¶Җн•ҳмӨ‘м—җ лҢҖн•ҳм—¬ нҢҢнҳ•к°•нҢҗмқҖ м—°м„ұкө¬мЎ°л¬јлЎң кұ°лҸҷн•ҳл©°, л’Өмұ„мӣҖ м§Җл°ҳкіј нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬ј к°„мқҳ мғҒнҳёмһ‘мҡ©мқ„ нҶөн•ҙ к°•нҢҗ лӮҙм—җлҠ” мЈјлЎң мӣҗнҷҳл°©н–Ҙмқҳ 압축л Ҙмқҙ л°ңмғқн•ҳм—¬ кө¬мЎ°м Ғмқё нҡЁмңЁм„ұмқ„ лҸ„лӘЁн• мҲҳ мһҲлӢӨ. мқҙлҹ¬н•ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҖ кІҪм ңм„ұкіј мӢңкіөм„ұмқҙ мҡ°мҲҳн•ҳм—¬ лҸ„лЎң л°Ҹ мІ лҸ„мқҳ н„°л„җ, м•”кұ°, мҲҳлЎң, мғқнғң көҗлҹүкіј к°ҷмқҖ мҶҢк·ңлӘЁ көҗлҹү л“ұ лӢӨм–‘н•ң л°©л©ҙм—җм„ң нҷңмҡ©лҗҳкі мһҲлӢӨ. Fig. 1мқҖ лҸ„лЎңкөҗм—җм„ң нҢҢнҳ•к°•нҢҗмқҙ н„°л„җлЎң мӮ¬мҡ©лҗң мӮ¬лЎҖлҘј ліҙм—¬мЈјкі мһҲлӢӨ.
н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ё(KEC, 2001)кіј к°ҷмқҖ нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬ј м„Өкі„кё°мӨҖм—җлҠ” мқҙмқҢл¶Җ мғҒм„ё к·ңм • л°Ҹ мқҙмқҢл¶Җ м•Ҳм „лҸ„ кІҖнҶ м Ҳм°Ёк°Җ м ңмӢңлҗҳм–ҙ мһҲлӢӨ. н•ҳм§Җл§Ң нҢҢнҳ•к°•нҢҗ ліјнҠё мқҙмқҢл¶Җм—җм„ң Fig. 2мҷҖ к°ҷмқҙ к°•нҢҗмқҳ к· м—ҙ, м°ўк№Җ, лҲ„мҲҳ л°Ҹ л…№мқҙ л°ңмғқн•ҳлҠ” мӮ¬лЎҖк°Җ к°„к°„нһҲ ліҙкі лҗҳкі мһҲлӢӨ.
кё°мЎҙ м—°кө¬м—җм„ңлҠ” мӢӨн—ҳмқҙлӮҳ н•ҙм„қмқ„ нҶөн•ҙ мқҙлҹ¬н•ң нҢҢнҳ•к°•нҢҗ ліјнҠё мқҙмқҢл¶Җмқҳ мҶҗмғҒ мӣҗмқёмқ„ к·ңлӘ…н•ҳкі к°ңм„ м•Ҳмқ„ м ңм•Ҳн•ҙ ліҙкі мһҗ л…ёл Ҙн•ң л°” мһҲлӢӨ. н•ҳм§Җл§Ң мӢӨн—ҳм Ғ м—°кө¬м—җ мһҲм–ҙм„ңлҠ” мӢӨн—ҳ비мҡ©мқҙлӮҳ мһҘ비 л“ұмқҳ м ңм•ҪмңјлЎң мқён•ҙ ліјнҠё мқҙмқҢл¶Җмқҳ лӢӨм–‘н•ң л°°м—ҙ л°Ҹ мғҒм„ёлҘј мӢӨн—ҳ ліҖмҲҳлЎң 충분нһҲ л°ҳмҳҒн•ҳм§Җ лӘ»н•ң н•ңкі„к°Җ мһҲлӢӨ(Mikhailovsky et al., 1992; Choi, 2005; Lee et al., 2007; Oh and Nam, 2012). н•ңнҺё мЈјлЎң мң н•ңмҡ”мҶҢлІ•мқ„ мқҙмҡ©н•ң н•ҙм„қм Ғ м—°кө¬м—җм„ң мһҲм–ҙм„ңлҸ„ ліјнҠё мқҙмқҢл¶Җмқҳ кө¬мЎ° кұ°лҸҷмқ„ н•©лҰ¬м ҒмңјлЎң лӘЁмӮ¬н• мҲҳ мһҲлҠ” мң н•ңмҡ”мҶҢ лӘЁлҚёмқ„ лҸ„м¶ңн•ҳл ӨлҠ” м—°кө¬к°Җ лҜёнқЎн–ҲлӢӨкі нҢҗлӢЁлҗңлӢӨ(Kang, 2004; Lee, 2012).
мқҙ м—°кө¬м—җм„ңлҠ” кё°мЎҙ м—°кө¬ліҙлӢӨ мўҖ лҚ” лӢӨм–‘н•ң ліҖмҲҳлҘј л°ҳмҳҒн•ҳкі мғҒм„ён•ң лӘЁлҚёмқ„ кө¬м„ұн•ҳм—¬ нҢҢнҳ•к°•нҢҗ ліјнҠё мқҙмқҢл¶Җмқҳ мң н•ңмҡ”мҶҢн•ҙм„қмқ„ мӢӨмӢңн•ҳкі , к·ё кІ°кіјлҘј 분м„қн•ҳм—¬ нҳ„мһ¬ мӮ¬мҡ©лҗҳкі мһҲлҠ” ліјнҠё мқҙмқҢл¶Җмқҳ нғҖлӢ№м„ұмқ„ нҸүк°Җн•ҳкі к°ңм„ м•Ҳмқ„ м ңм•Ҳн•ҙ ліҙм•ҳлӢӨ.
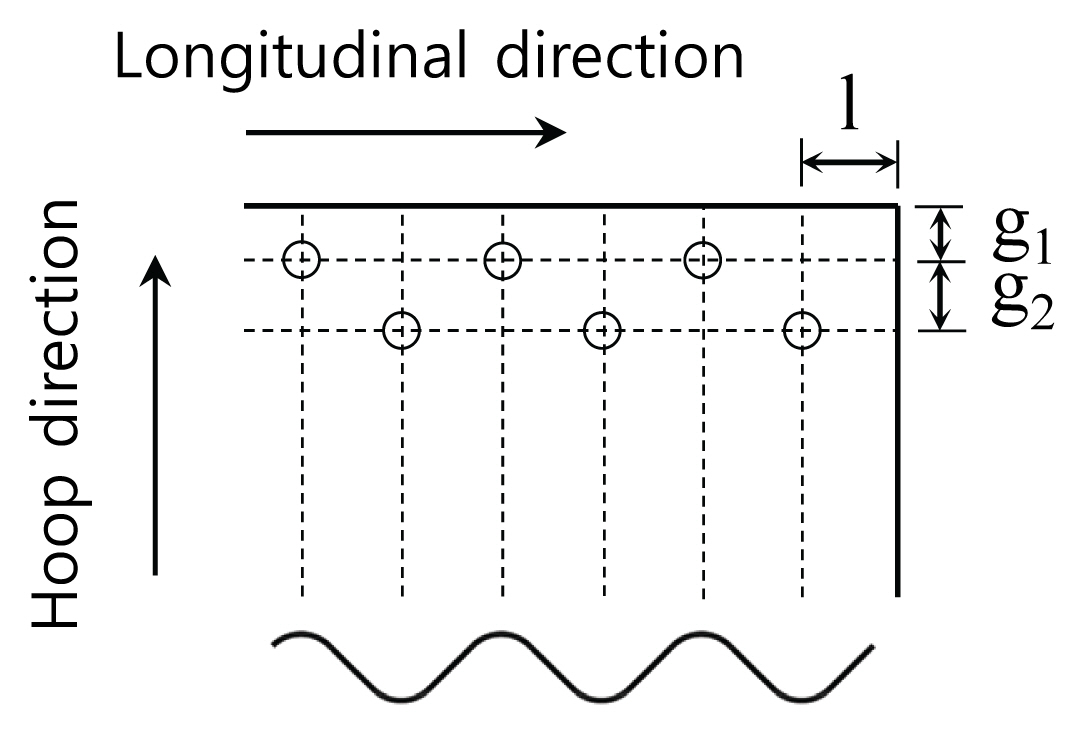
нҢҢнҳ•к°•нҢҗмқҖ к·ңкІ©м—җ л”°лқј н‘ңмӨҖнҳ• л°Ҹ лҢҖкіЁнҳ•мқҙ мӮ¬мҡ©лҗҳкі мһҲмңјл©°, көӯлӮҙм—җм„ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬ј м„Өкі„лҘј мң„н•ҙ к°ҖмһҘ лІ”мҡ©м ҒмңјлЎң м°ёмЎ°н•ҳлҠ” к·ңм •мқҖ н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ё(KEC, 2001)мқҙлӢӨ. мқҙм—җ л”°лҘҙл©ҙ н‘ңмӨҖнҳ•мқҳ к°•нҢҗ л‘җк»ҳлҠ” 2.7вҲј7 mm, кіЁмқҳ н”јм№ҳ л°Ҹ к№ҠмқҙлҠ” к°Ғк°Ғ 150 mm л°Ҹ 50 mmмқҙл©°, нҢҢнҳ•мқҳ көҪнһҳл°ҳм§ҖлҰ„мқҖ 28 mmмқҙлӢӨ. н•ңнҺё нҢҢнҳ•к°•нҢҗ ліјнҠё мқҙмқҢл¶Җм—җм„ң ліјнҠё мЎ°мһ„ нҶ нҒ¬ лІ”мң„лҠ” 200вҲј400 NВ·mлЎң к·ңм •н•ҳкі мһҲлӢӨ. лҳҗн•ң ліјнҠё мқҙмқҢл¶Җмқҳ к°•лҸ„лҘј м§ҒкІҪ 20 mm ліјнҠёлҘј кё°мӨҖмңјлЎң к°•нҢҗ л‘җк»ҳ л°Ҹ ліјнҠё к°ңмҲҳм—җ л”°лқј м ңкіөн•ҳкі мһҲлӢӨ.
ліјнҠё мқҙмқҢл¶Җм—җм„ң к°•нҢҗл“Өмқҳ кІ№м№Ёкіј кҙҖл Ёлҗң к·ңм •мқҖ Fig. 3мқ„ м°ёмЎ°н• л•Ң н‘ңмӨҖнҳ•мқҳ кІҪмҡ° 축방н–Ҙ м—°лӢЁкұ°лҰ¬ l = 50 mm, мӣҗнҷҳл°©н–Ҙ м—°лӢЁкұ°лҰ¬ g1 = 35 mm, мӣҗнҷҳл°©н–Ҙ ліјнҠё к°„кІ© g2 = 50 mmмқҙлӢӨ. мқҙлҠ” KS D 3590 (2017) кё°мӨҖкіј лҸҷмқјн•ҳлӢӨ. н•ңнҺё мәҗлӮҳлӢӨмқҳ CHBDC (CSA, 2006) л°Ҹ лҜёкөӯмқҳ AISI (2002) к·ңм •м—җм„ңлҠ” l = 50 mm мқҙмғҒ, g1 = 32 mm мқҙмғҒ, g2 = 50.8 mm мқҙмғҒмңјлЎң к·ңм •н•ҳкі мһҲмңјлҜҖлЎң көӯлӮҙ к·ңм •кіј мң мӮ¬н•ҳлӢӨ. Fig. 3мқҖ н‘ңмӨҖнҳ•м—җм„ң н”јм№ҳлӢ№ 2ліјнҠёк°Җ мӮ¬мҡ©лҗң кІҪмҡ°мқҙл©°, 3ліјнҠё л°Ҹ 4ліјнҠёмқҳ кІҪмҡ°м—җлҸ„ 2ліјнҠё л°°м—ҙ мӮ¬мқҙм—җ ліјнҠёл§Ң 추к°Җлҗ лҝҗ кҙҖл Ё к·ңм •мқҖ лҸҷмқјн•ҳлӢӨ.
Bakht and Agarwal (1988)мқҖ Fig. 4(a)мҷҖ к°ҷмқҙ ліјнҠё мқҙмқҢл¶Җм—җ нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н• кІҪмҡ° B-Bм—ҙліҙлӢӨлҠ” C-Cм—ҙм—җ мң„м№ҳн•ң ліјнҠёк°Җ лҚ” нҒ° нһҳмқ„ л°ӣкІҢ лҗҳлҜҖлЎң C-Cм—ҙ ліјнҠё кө¬л©Қ мЈјліҖмқҳ к°•нҢҗмқҙ мҶҗмғҒлҗ к°ҖлҠҘм„ұмқҙ лҚ” нҒ¬лӢӨкі м§Җм Ғн•ҳмҳҖлӢӨ. н•ңнҺё Mikhailovsky et al. (1992)мқҖ Fig. 4(b)мҷҖ к°ҷмқҙ нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н• л•Ң ліјнҠёмқҳ м •л°°м—ҙ(correct joint lap)кіј л¶Җл°°м—ҙ(incorrect joint lap) мӨ‘м—җм„ң л¶Җл°°м—ҙ ліјнҠё мЈјліҖ к°•нҢҗм—җ к· м—ҙмқҙ л°ңмғқн• нҷ•лҘ мқҙ лҚ” нҒ¬лӢӨкі м§Җм Ғн•ҳмҳҖлӢӨ. кІ°көӯ Bakht and AgarwalмқҖ Mikhailovsky et al.кіј лҸҷмқјн•ң нҳ„мғҒмқ„ м–ёкёүн•ҳкі мһҲлӢӨ. мқҙ л…јл¬ём—җм„ң м •л¶Җл°°м—ҙмқҙлқјлҠ” мҡ©м–ҙлҠ” ліјнҠё л°°м—ҙмқҳ мҳікі к·ёлҰ„ліҙлӢӨлҠ” нңЁлӘЁл©ҳнҠё м Җн•ӯм„ұмқҳ мң л¶ҲлҰ¬мқҳ мқҳлҜёлЎң мӮ¬мҡ©лҗҳм—ҲлӢӨ.
Kang (2004)мқҖ көӯлӮҙмҷё м„Өкі„кё°мӨҖм—җ м ңмӢңлҗң нҢҢнҳ•к°•нҢҗмқҳ кІ№м№ЁкёёмқҙлӮҳ м—°лӢЁкұ°лҰ¬ к·ңм •мқҖ кІҪн—ҳм—җ мқҳмЎҙн•ҳкі мһҲмңјл©° мқҙм—җ лҢҖн•ң мқҙлЎ м Ғ, н•ҙм„қм Ғ м—°кө¬к°Җ л¶ҖмЎұн•ҳлӢӨкі м§Җм Ғн•ҳмҳҖлӢӨ. мқҙм—җ ABAQUSмқҳ мүҳмҡ”мҶҢлҘј мӮ¬мҡ©н•ң н•ҙм„қмқ„ мӢӨмӢңн•ҳмҳҖмңјл©°, ліҖмҲҳлҠ” к°•нҢҗ нҳ•нғң(н‘ңмӨҖнҳ•, лҢҖкіЁнҳ•), 축방н–Ҙ м—°лӢЁкұ°лҰ¬ l (25вҲј50 mm), к°•нҢҗ л‘җк»ҳ(3.2вҲј7 mm), мӣҗнҷҳл°©н–Ҙ м—°лӢЁкұ°лҰ¬ g1 (15вҲј50 mm), мӣҗнҷҳл°©н–Ҙ ліјнҠё к°„кІ© g2 (48вҲј90 mm)мҳҖлӢӨ. н•ҙм„қ кІ°кіјм—җ к·јкұ°н•ҳм—¬ н‘ңмӨҖнҳ•мқҳ кІҪмҡ° м Ғм Ҳн•ң мқҙмқҢл¶Җ нҳ•мғҒмңјлЎң l вүҘ 35 mm, g1 вүҘ 35 mm, g2 вүҘ 50 mmлҘј м ңм•Ҳн•ҳмҳҖмңјл©°, л”°лқјм„ң нҳ„мһ¬ мӮ¬мҡ©лҗҳлҠ” н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ёмқҙ нғҖлӢ№н•ҳлӢӨкі мЈјмһҘн•ҳмҳҖлӢӨ. н•ҳм§Җл§Ң мқҙлҠ” 압축л Ҙм—җ лҢҖн•ҙм„ңл§Ң кІҖнҶ н•ң кІ°кіјлЎңм„ң нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н•ҳлҠ” кІҪмҡ°к№Ңм§Җ мң нҡЁн•ң кІ°лЎ мңјлЎң ліҙкё°лҠ” м–ҙл өлӢӨ.
Lee et al. (2007)мқҖ 2ліјнҠё л°°м—ҙм—җ лҢҖн•ҳм—¬ мқҙмқҢл¶Җ мӮ¬мқҙмқҳ к°ңмҠӨнӮ· мң л¬ҙ, ліјнҠё м ‘н•© мӢң мҷҖм…” мң л¬ҙ, ліјнҠё кө¬л©Қ мІңкіө мӢң лҸҢм¶ңл¶Җ мң л¬ҙ, м •л°°м—ҙ л°Ҹ л¶Җл°°м—ҙ, к°•нҢҗ л‘җк»ҳ(3.2вҲј6 mm)лҘј ліҖмҲҳлЎң 압축мӢңн—ҳ л°Ҹ нңЁмӢңн—ҳмқ„ лі„лҸ„лЎң мӢӨмӢңн•ҳмҳҖлӢӨ. к·ё кІ°кіј к°ңмҠӨнӮ·мқҙ мқҙмқҢл¶Җ кұ°лҸҷм—җ лҜём№ҳлҠ” мҳҒн–ҘмқҖ нҒ¬м§Җ м•ҠмқҖ кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ. мҷҖм…”мқҳ кІҪмҡ° 압축 лҳҗлҠ” нңЁ кұ°лҸҷ м—¬л¶Җ л°Ҹ к°•нҢҗ л‘җк»ҳм—җ л”°лқј м°Ёмқҙк°Җ мһҲм—Ҳм§Җл§Ң к·№н•ңн•ҳмӨ‘ мёЎл©ҙм—җм„ң лӘ…нҷ•н•ң нҡЁкіјлҠ” м—Ҷм—ҲлӢӨ. лҳҗн•ң ліјнҠё кө¬л©Қ лҸҢм¶ңл¶Җ мң л¬ҙлҸ„ к·№н•ңн•ҳмӨ‘м—җ кұ°мқҳ мҳҒн–Ҙмқ„ лҜём№ҳм§Җ м•Ҡм•ҳлӢӨ. мЈјлӘ©н• л§Ңн•ң м җмңјлЎң нңЁ кұ°лҸҷ мӢң ліјнҠёмқҳ м •л°°м—ҙкіј л¶Җл°°м—ҙмқҙ к·№н•ңн•ҳмӨ‘м—җ лҜём№ҳлҠ” мҳҒн–ҘмқҖ нҒ¬м§Җ м•Ҡм•ҳмңјлӮҳ, л¶Җл°°м—ҙм—җм„ңлҠ” к·№н•ңн•ҳмӨ‘ мқҙнӣ„ ліјнҠёл¶Җ мЈјліҖ к°•нҢҗм—җ к· м—ҙмқҙ л°ңмғқн•ҳм—¬ н•ҳмӨ‘мқҙ кёүкІ©нһҲ к°җмҶҢн•ҳлҠ” кІҪн–Ҙмқҙ кҙҖм°°лҗҳм—Ҳмңјл©°, мқҙлҹ¬н•ң нҳ„мғҒмқҖ нҠ№нһҲ л‘җк»ҳк°Җ 6 mmлЎң л‘җкәјмҡё л•Ң л‘җл“ңлҹ¬м§„ кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ.
Lee (2012)лҠ” лҢҖкіЁнҳ• нҢҢнҳ•к°•нҢҗмқҳ л‘җк»ҳ л°Ҹ ліјнҠё м§ҒкІҪмқ„ ліҖмҲҳлЎң н•ң мӢӨн—ҳ кІ°кіјмҷҖ LS-DYNAмқҳ мҶ”лҰ¬л“ңмҡ”мҶҢлҘј мқҙмҡ©н•ң н•ҙм„қ кІ°кіјлҘј 비көҗн•ҳм—¬ мҲҳм№ҳн•ҙм„қ лӘЁлҚёмқҳ нғҖлӢ№м„ұмқ„ кІҖмҰқн•ҳмҳҖмңјл©°, мҲҳм№ҳн•ҙм„қмқ„ нҶөн•ҳм—¬ мӢӨм ң кұ°лҸҷмқ„ л§Өмҡ° мң мӮ¬н•ҳкІҢ мҳҲмёЎн• мҲҳ мһҲмқҢмқ„ мЈјмһҘн•ҳмҳҖлӢӨ. н•ҳм§Җл§Ң мқҙ м—°кө¬ лҳҗн•ң 압축л Ҙм—җ лҢҖн•ҙм„ңл§Ң кІҖнҶ н•ҳмҳҖлӢӨлҠ” м ңн•ңм җмқҙ мһҲлӢӨ.
к·ё мҷё кё°мЎҙмқҳ мӢӨн—ҳм Ғ м—°кө¬лҘј мӮҙнҺҙліҙл©ҙ нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬ј м„Өкі„ мӢң мЈјмҡ” к°Җм •мқё 압축л Ҙм—җ лҢҖн•ҙм„ңл§Ң мӢӨн—ҳмқ„ мӢӨмӢңн•ң кІҪмҡ°л“Өмқҙ мһҲм—ҲлӢӨ(Oh and Nam, 2012). н•ҳм§Җл§Ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬ј ліјнҠё мқҙмқҢл¶Җм—җм„ң л°ңмғқн•ҳлҠ” мҶҗмғҒмқҳ мЈјмҡ” мӣҗмқёмқҙ 압축 кұ°лҸҷліҙлӢӨлҠ” нңЁ кұ°лҸҷкіј кҙҖл ЁлҗңлӢӨлҠ” м җмқҙ нҢҢм•…лҗЁм—җ л”°лқј ліјнҠё мқҙмқҢл¶Җ кІҖнҶ лҘј мң„н•ҙм„ң 압축 мӢӨн—ҳкіј лҚ”л¶Ҳм–ҙ нңЁ мӢӨн—ҳмқ„ мӢӨмӢңн•ҳлҠ” кІҪмҡ°к°Җ мҰқк°Җн•ҳмҳҖлӢӨ(Choi, 2005; Lee et al., 2007). н•ҳм§Җл§Ң, мӢӨм ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҳ кұ°лҸҷмқҖ 압축л Ҙкіј нңЁлӘЁл©ҳнҠёлҘј лҸҷмӢңм—җ л°ӣкі мһҲм§Җл§Ң мӢӨн—ҳм—җм„ңлҠ” лҢҖл¶Җ분 압축 мӢӨн—ҳкіј нңЁ мӢӨн—ҳмқ„ лі„лҸ„лЎң мӢӨмӢңн•ҳм—¬ мӢӨкө¬мЎ°л¬јмқҳ кұ°лҸҷмқ„ 충분нһҲ лӘЁмӮ¬н•ҳкі мһҲм§Җ лӘ»н•ң лӢЁм җмқҙ мһҲлӢӨкі мғқк°ҒлҗңлӢӨ. мқҙмІҳлҹј мӢӨн—ҳмІҙм—җ 압축л Ҙкіј нңЁлӘЁл©ҳнҠёлҘј лҸҷмӢңм—җ к°Җн•ҳм§Җ лӘ»н•ң кІғмқҖ мӢӨн—ҳ мһҘм№ҳмқҳ м ңм•ҪмқҙлӮҳ мӢӨн—ҳ мӢң н•ҳмӨ‘ лҳҗлҠ” ліҖмң„ м ңм–ҙмқҳ м–ҙл ӨмӣҖм—җ кё°мқён•ң кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ. мқҙлҹ¬н•ң мӢӨн—ҳ мӢңмқҳ м• лЎңм җл“ӨмқҖ н•©лҰ¬м Ғмқё мҲҳм№ҳн•ҙм„қ лӘЁлҚёмқҙ кө¬м„ұлҗҳм—ҲлӢӨлҠ” м „м ңн•ҳм—җ мң н•ңмҡ”мҶҢлІ• л“ұ м „мӮ°кө¬мЎ°н•ҙм„қмқ„ нҶөн•ң м ‘к·јмқ„ нҶөн•ҙ н•ҙкІ° к°ҖлҠҘн• кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ.
көӯлӮҙ нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҳ мқҙмқҢл¶Җ м„Өкі„м—җ мӮ¬мҡ©лҗҳлҠ” н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ё(KEC, 2001)мқҳ мқҙмқҢл¶Җ к°•лҸ„ к·ңм •мқҖ к°ҖмһҘ мқҙмғҒм Ғмқё мғҒнҷ©мқ„ к°Җм •н•ҳм—¬ нҢҢнҳ•к°•нҢҗм—җ нңЁлӘЁл©ҳнҠёлҠ” л°ңмғқн•ҳм§Җ м•Ҡкі м••м¶•л Ҙл§Ң мһ‘мҡ©н• л•Ңмқҳ к°•лҸ„мқҙл©°, мӢӨн—ҳм—җ к·јкұ°н•ҳм—¬ лҸ„м¶ңлҗң кІғмңјлЎң м•Ңл Өм ё мһҲлӢӨ. н•ҳм§Җл§Ң мӢӨм ңлЎңлҠ” мӢңкіөмӨ‘ лҳҗлҠ” кіөмҡ©мӨ‘м—җ 압축л Ҙкіј лҚ”л¶Ҳм–ҙ л¶Ҳк°Җн”јн•ң нңЁлӘЁл©ҳнҠёлҸ„ л°ңмғқн•ҳлҠ” кІҪмҡ°к°Җ лҢҖл¶Җ분мқҙлҜҖлЎң мқҙлҹ¬н•ң мқҙмқҢл¶Җ к°•лҸ„ к·ңм •мқҙ 충분н•ң м•Ҳм „м„ұмқ„ лӢҙліҙн•ҳкі мһҲм§ҖлҠ” лӘ»н•ҳлӢӨкі мғқк°ҒлҗңлӢӨ. нҠ№нһҲ нңЁлӘЁл©ҳнҠё мһ‘мҡ© мӢң кё°мЎҙм—җ л¬ём ңк°Җ м ңкё°лҗҳм—ҲлҚҳ ліјнҠёмқҳ м •л°°м—ҙмқҙлӮҳ л¶Җл°°м—ҙ(Bakht and Agarwal, 1988; Mikhailovsky et al., 1992) м—¬л¶Җк°Җ ліјнҠё мқҙмқҢл¶Җ кұ°лҸҷмқҳ мЈјмҡ” мҳҒн–Ҙмқёмһҗлқјл©ҙ нҶөмғҒм ҒмңјлЎң мӮ¬мҡ©н•ҳлҚҳ м—°лӢЁкұ°лҰ¬ к·ңм •мқҙлӮҳ ліјнҠё к°„кІ© к·ңм •м—җ лҢҖн•ң мһ¬кі мқҳ м—¬м§Җк°Җ мһҲлӢӨ. л”°лқјм„ң ліјнҠё мқҙмқҢл¶Җмқҳ мҶҗмғҒ л©”м»ӨлӢҲмҰҳмқ„ мҳ¬л°”лЎң л°қнһҲкё° мң„н•ҙм„ңлҠ” мӢӨн—ҳм Ғ лҳҗлҠ” н•ҙм„қм Ғмқё 추к°Җ кІҖмҰқмқҙ н•„мҡ”н•ҳлӢӨ.
мқҙ м—°кө¬м—җм„ңлҠ” мӢӨм ң л°ңмғқн• к°ҖлҠҘм„ұмқҙ нҒ° мҲҳмӨҖмқҳ 압축л Ҙкіј нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н• л•Ң ліјнҠё мқҙмқҢл¶Җ мЈјліҖмқҳ к°•нҢҗм—җм„ң л°ңмғқн•ҳлҠ” мқ‘л Ҙмқҳ нҒ¬кё°лҘј кІҖнҶ н•ЁмңјлЎңмҚЁ нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җм„ң кҙҖм°°лҗҳлҠ” ліјнҠё мқҙмқҢл¶Җмқҳ к· м—ҙмқҙлӮҳ мҶҗмғҒмқҳ мӣҗмқём—җ лҢҖн•ҙ кі м°°н•ҙ ліҙм•ҳлӢӨ. лҳҗн•ң, ліјнҠё к°ңмҲҳ, ліјнҠёмқҳ м •л°°м—ҙ л°Ҹ л¶Җл°°м—ҙ, м—°лӢЁкұ°лҰ¬, ліјнҠё к°„кІ©мқ„ ліҖмҲҳлЎң н•ҳм—¬ н•ҙм„қмқ„ мҲҳн–үн•ЁмңјлЎңмҚЁ мқҙлҹ¬н•ң ліјнҠё мқҙмқҢл¶Җ к°•нҢҗ мҶҗмғҒмқ„ мҷ„нҷ”н• мҲҳ мһҲлҠ” л°©м•Ҳмқ„ нҢҢм•…н•ҙ ліҙм•ҳлӢӨ. н•ҙм„қм—җлҠ” м „м„ёкі„м ҒмңјлЎң нҶөмҡ©лҗҳлҠ” л№„м„ нҳ• мң н•ңмҡ”мҶҢн•ҙм„қ н”„лЎңк·ёлһЁмқё ABAQUS (Dassault SystГЁmes Simulia, 2015)лҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ.
мҲҳм№ҳн•ҙм„қмқ„ нҶөн•ң 분м„қ лҢҖмғҒмқҖ к·ёк°„ ліјнҠё мқҙмқҢл¶Җ мҶҗмғҒ мӮ¬лЎҖк°Җ лҚ” л§Һмқҙ ліҙкі лҗҳм—ҲлҚҳ н‘ңмӨҖнҳ• нҢҢнҳ•к°•нҢҗмқҙл©°, к°•нҢҗ л‘җк»ҳлҠ” к·ёк°„ мӮ¬мҡ©лҗҳм—ҲлҚҳ 2.7вҲј7 mm лІ”мң„ мӨ‘ 비көҗм Ғ л№ҲлІҲнһҲ мӮ¬мҡ©лҗҳкі л‘җк»ҳк°Җ м–ҮмқҖ нҺём—җ мҶҚн•ҳм—¬ мҶҗмғҒм—җ м·Ём•Ҫн• кІғмңјлЎң мҳҲмғҒлҗҳлҠ” 4 mmлҘј кі л Өн•ҳмҳҖлӢӨ. мӣҗнҷҳл°©н–Ҙ кіЎлҘ л°ҳкІҪ(R)мқҖ кө¬мЎ°л¬ј к·ңлӘЁм—җ л”°лқј ліҖлҸҷн•ҳм§Җл§Ң мӢӨм ң л№ҲлІҲнһҲ мӮ¬мҡ©лҗҳлҠ” R = 3.25 mлҘј лҢҖмғҒмңјлЎң н•ҳмҳҖлӢӨ. н‘ңмӨҖнҳ• нҢҢнҳ•к°•нҢҗмқҳ кІҪмҡ° нҶ н”јк°Җ л§Өмҡ° к№ҠмқҖ кІҪмҡ°лҘј м ңмҷён•ҳкі лҠ” кұ°мқҳ лҢҖл¶Җ분 н”јм№ҳлӢ№ 2к°ңмқҳ ліјнҠёлҘј л°°м№ҳн•ҳлҠ” 2ліјнҠё мӢңмҠӨн…ңмқҙ мӮ¬мҡ©лҗҳкі мһҲмңјлҜҖлЎң мқҙлҘј кё°ліём•ҲмңјлЎң н•ҳмҳҖлӢӨ. н•ҙм„қ кё°ліём•Ҳм—җлҠ” н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ёмқҳ м—°лӢЁкұ°лҰ¬ л°Ҹ ліјнҠё к°„кІ© к·ңм •мқ„ м Ғмҡ©н–Ҳмңјл©°, 3.3м Ҳм—җм„ң м–ёкёүн• ліҖмҲҳ н•ҙм„қм—җм„ңлҠ” мқҙлҹ¬н•ң ліјнҠё к°ңмҲҳлӮҳ кҙҖл Ё к·ңм •л“Өмқ„ ліҖлҸҷмӢңмјң ліҙм•ҳлӢӨ.
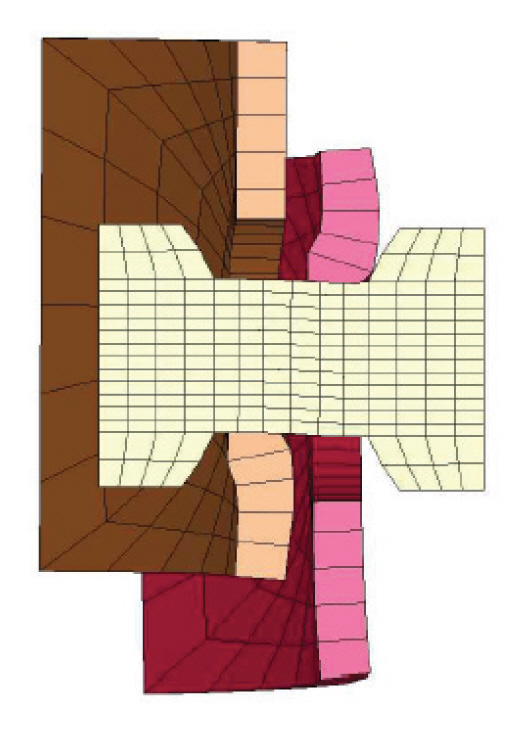
ліјнҠё, л„ҲнҠё л°Ҹ к°•нҢҗ мӮ¬мқҙм—җлҠ” м ‘мҙүл©ҙмқҙ мЎҙмһ¬н•ҳкі м ‘мҙүл©ҙм—җм„ңлҠ” ліјнҠёмқҳ нҶ нҒ¬, нңЁ кұ°лҸҷ л°Ҹ мқёмһҘ/압축 кұ°лҸҷ л“ұм—җ мқҳн•ҳм—¬ л§Ҳм°°мқҙ мЎҙмһ¬н•ҳкі мһҲмңјлҜҖлЎң мҲҳм№ҳн•ҙм„қ мӢң м ‘мҙүл©ҙмқҳ м •мқҳ л°Ҹ м„ұм§Ҳ л¶Җм—¬ л“ұ м ‘мҙү н•ҙм„қ(contact analysis) кё°лІ•мқҙ н•„мҡ”н•ҳлӢӨ. н•ҳм§Җл§Ң кё°мЎҙмқҳ н•ҙм„қм Ғ м—°кө¬лҘј мӮҙнҺҙліҙл©ҙ мң н•ңмҡ”мҶҢ лӘЁлҚём—җм„ң к°ңм„ мқҙ н•„мҡ”н•ң м җл“Өмқҙ л°ңкІ¬лҗңлӢӨ. мҳҲлҘј л“Өм–ҙ, Fig. 5мҷҖ к°ҷмқҖ кё°мЎҙ м—°кө¬(Lee, 2012)м—җм„ңлҠ” к°•нҢҗмқ„ мҶ”лҰ¬л“ңмҡ”мҶҢлЎң лӘЁлҚёл§Ғн•ҳмҳҖлҠ”лҚ°, к°•нҢҗ л‘җк»ҳ л°©н–ҘмңјлЎң 1мёөмңјлЎңл§Ң л¶„н• н•ЁмңјлЎңм„ң мҶ”лҰ¬л“ңмҡ”мҶҢмқҳ нҠ№м„ұмқ„ кі л Өн• л•Ң нңЁлӘЁл©ҳнҠё мһ‘мҡ© мӢң к°•нҢҗмқҳ нңЁ кұ°лҸҷмқ„ мҳ¬л°”лЎң лӘЁмӮ¬н• мҲҳ м—ҶлӢӨлҠ” лӢЁм җмқҙ мһҲлӢӨ. лҳҗн•ң ліјнҠёмқҳ мһҗмң лЎңмҡҙ нҡҢм „мқ„ ліјнҠё мғҒн•ҳл©ҙ кІҪкі„мЎ°кұҙмқ„ нҶөн•ҙ кө¬мҶҚн•ҳм—¬ мӢӨм ң кұ°лҸҷкіјмқҳ м°Ёмқҙк°Җ мҳҲмғҒлҗңлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” мқҙлҹ¬н•ң нҢҢнҳ•к°•нҢҗ ліјнҠё мқҙмқҢл¶Җмқҳ кё°мЎҙ мҲҳм№ҳн•ҙм„қ лӘЁлҚёмқҳ лӢЁм җл“Өмқ„ к°ңм„ н•ҳм—¬ мӢ лў°м„ұ мһҲкі н•©лҰ¬м Ғмқё лӘЁлҚёмқ„ кө¬м„ұн•ҳкі мһҗ л…ёл Ҙн•ҳмҳҖлӢӨ.
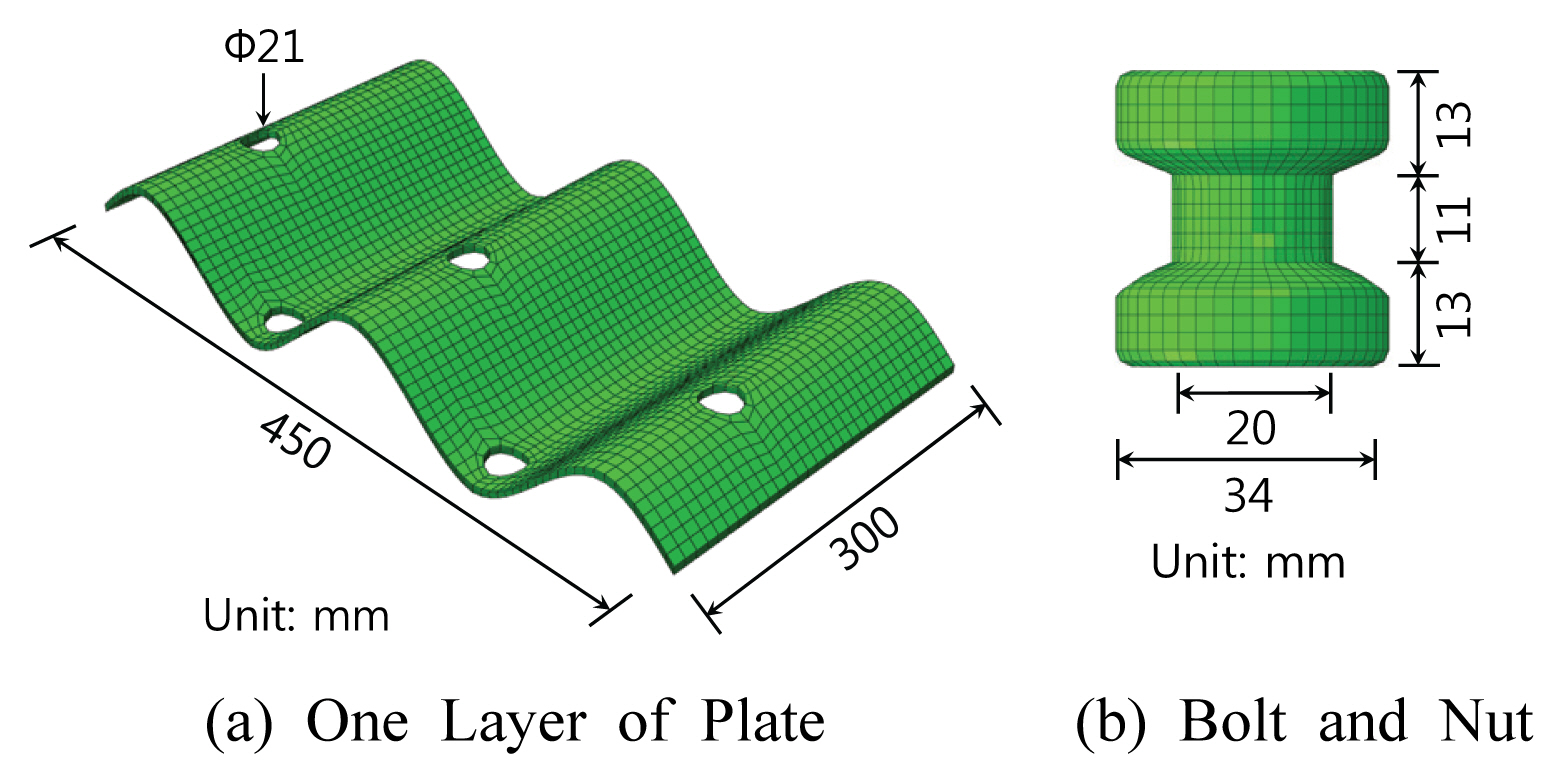
충분нһҲ 세분нҷ”н•ң мң н•ңмҡ”мҶҢл§қмқ„ мқҙмҡ©н•ҳм—¬ м •л°Җн•ң н•ҙм„қмқ„ мҲҳн–үн•ҳкі мһҗ нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҳ л¶Җ분 лӘЁлҚёмқ„ кө¬м„ұн•ҳмҳҖлӢӨ. м—„л°Җн•ң нҳ•мғҒ лӘЁлҚёл§Ғмқ„ мң„н•ҳм—¬ н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ё(KEC, 2001)м—җ м ңмӢңлҗң нҢҢнҳ• нҳ•мғҒмқ„ м°ёмЎ°н•ҳлҗҳ, мқҙм—җ л¶Җк°Җн•ҳм—¬ Fig. 6кіј к°ҷмқҙ мӢӨм ң нҢҢнҳ•к°•нҢҗ л°Ҹ кө¬м„ұн’Ҳмқ„ м°ёмЎ°н•ҳм—¬ нҳ•мғҒмқҙлӮҳ м№ҳмҲҳлҘј кІҖмҰқн•ҳмҳҖлӢӨ.
л¶Җ분 лӘЁлҚёмқҖ Fig. 7(a)мқҳ нҢҢнҳ•к°•нҢҗмқҙ 2мһҘ кІ№м№ң нҳ•нғңмқҙлӢӨ. мқҙл•Ң нҢҢнҳ•мқҖ көҪнһҳл°ҳм§ҖлҰ„ к·ңм •к№Ңм§Җ кі л Өн•ҳм—¬ м—„л°Җн•ң нҳ•мғҒмңјлЎң лӘЁлҚёл§Ғн•ҳмҳҖлӢӨ. л¶Җ분 лӘЁлҚёмқҖ м—°мҶҚлҗң м „мІҙ кө¬мЎ°л¬ј мӨ‘ мқјл¶ҖлҘј мһҳлқј лӮё кІғмқҙлҜҖлЎң мһҳлҰ° лӢЁл©ҙм—җ мһ‘мҡ©н•ҳлҠ” мқ‘л ҘмқҙлӮҳ лӢЁл©ҙл Ҙмқ„ мҳ¬л°”лЎң лӘЁмӮ¬н•ҙм•ј мӢӨм ң кұ°лҸҷкіј мң мӮ¬н•ҳкІҢ лҗңлӢӨ. лҳҗн•ң мһҳлҰ° лӢЁл©ҙмқ„ кө¬мҶҚн•ҳлҠ” кІҪкі„мЎ°кұҙм—җ л”°лқј мӢӨм ң кұ°лҸҷкіј м°Ёмқҙк°Җ л°ңмғқн• мҲҳ мһҲмңјлҜҖлЎң к°Җкёүм Ғ л¶Җ분 лӘЁлҚёмқҳ ліҖнҳ•мқҙ мһҗмң лЎӯкІҢ л°ңмғқн• мҲҳ мһҲлҸ„лЎқ кІҪкі„мқҳ кө¬мҶҚмЎ°кұҙмқҖ мөңмҶҢнҷ”н•ҳлҠ” кІғмқҙ л°”лһҢм§Ғн•ҳлӢӨ. нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҖ мў…л°©н–Ҙ(нҶөлЎңл°©н–Ҙ)мңјлЎң кёёмқҙк°Җ кёҙ кө¬мЎ°л¬јлЎңм„ң мў…л°©н–ҘмңјлЎңлҠ” нҶ м•• л“ұ мҷёл¶Җн•ҳмӨ‘м—җ лҢҖн•ҙ мң мӮ¬н•ң кө¬мЎ° кұ°лҸҷмқ„ ліҙмқҙлҜҖлЎң мў…л°©н–Ҙ кёёмқҙк°Җ мӨ‘мҡ”н•ң кІғмқҖ м•„лӢҲм§Җл§Ң, м•һм„ң м–ёкёүн–Ҳл“Ҝ л¶Җ분 лӘЁлҚёмқҳ кІҪкі„мЎ°кұҙ мҳҒн–Ҙмқ„ кі л Өн•ҳм—¬ мў…л°©н–Ҙ кёёмқҙлҠ” 3к°ң н”јм№ҳм—җ н•ҙлӢ№н•ҳлҠ” 450 mmлЎң н•ҳмҳҖлӢӨ. 1к°ң к°•нҢҗмқҳ нҡЎл°©н–Ҙ(мӣҗнҷҳл°©н–Ҙ) кёёмқҙлҠ” 300 mmлЎң л‘җм—Ҳмңјл©°, к°•нҢҗ 2мһҘмқҙ кІ№міҗм ё мһҲмңјлҜҖлЎң м—°лӢЁкұ°лҰ¬лӮҳ ліјнҠё к°„кІ© к·ңм •мқ„ кі л Өн•ҳл©ҙ кё°ліём•Ҳмқҳ кІҪмҡ° 2ліјнҠё, 3ліјнҠё л°Ҹ 4ліјнҠё л¶Җл°°м—ҙмқҖ 480 mm, 4ліјнҠё м •л°°м—ҙмқҳ кІҪмҡ° 430 mmк°Җ лҗңлӢӨ. нҡЎл°©н–Ҙ кІҪкі„м—җлҠ” 압축л ҘмқҙлӮҳ нңЁлӘЁл©ҳнҠёлҘј к°Җн•ҳкІҢ лҗҳлҠ”лҚ°, нҡЎл°©н–Ҙ кёёмқҙк°Җ л„Ҳл¬ҙ кёё кІҪмҡ° мүҳ мқҙлЎ (Calladine, 1983)м—җ л”°лҘҙл©ҙ нҢҢнҳ• кіЎлҘ мқҳ мҳҒн–ҘмңјлЎң мқён•ҙ кІҪкі„лЎңл¶Җн„° л©Җм–ҙм§ҲмҲҳлЎқ нңЁлӘЁл©ҳнҠёк°Җ к°җмҶҢн•ҳм—¬ л¶Җ분 лӘЁлҚёмқҳ мӨ‘мӢ¬л¶Җм—җм„ңлҠ” мқҳлҸ„н•ң нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н•ҳм§Җ м•Ҡмқ„ мҡ°л Өк°Җ мһҲлӢӨ. л”°лқјм„ң мқҙ м—°кө¬м—җм„ңлҠ” мқҙлҹ¬н•ң мҳҒн–Ҙмқ„ кі л Өн•ҳм—¬ мөңмҶҢлЎң н•„мҡ”н•ң нҡЎл°©н–Ҙ кёёмқҙлҘј м·Ён•ҳмҳҖлӢӨ. лҳҗн•ң мӢӨм ңлЎңлҠ” нҡЎл°©н–Ҙ кіЎлҘ мқҙ мһҲлҚ”лқјлҸ„ мқҙмІҳлҹј 짧мқҖ нҡЎл°©н–Ҙ кёёмқҙлҘј к°Җ진 л¶Җ분 лӘЁлҚём—җм„ңлҠ” мҳҒн–Ҙмқҙ лҜёлҜён•ҳлҜҖлЎң к·ёлҹ¬н•ң нҡЎл°©н–Ҙ кіЎлҘ мқ„ кі л Өн•ҳм§Җ м•Ҡм•ҳлӢӨ.
ліјнҠёлҠ” Fig. 7(b)мҷҖ к°ҷмқҙ нҶөмғҒм ҒмңјлЎң мӮ¬мҡ©лҗҳлҠ” 20 mm м§ҒкІҪмқҳ ліјнҠё мӨ„кё°лҘј к°Җ진 ліјнҠёлҘј лӘЁлҚёл§Ғн•ҳмҳҖлӢӨ. мӢӨм ңлЎңлҠ” Fig. 6(b)мҷҖ к°ҷмқҙ ліјнҠё лЁёлҰ¬ л°Ҹ мӨ„кё°, л„ҲнҠёлЎң кө¬м„ұлҗҳм§Җл§Ң ліјнҠё лЁёлҰ¬мҷҖ л„ҲнҠёлҠ” мң мӮ¬н•ң нҳ•мғҒмқ„ к°Җм§ҖлҜҖлЎң лҸҷмқјн•ң нҳ•нғңлЎң мқјмІҙлЎң лӘЁлҚёл§Ғн•ҳмҳҖлӢӨ. ліјнҠё кө¬л©Қмқҳ м§ҒкІҪмқҖ мӢңкіө мҳӨм°Ё л°Ҹ ліјнҠёмҷҖ л„ҲнҠё мІҙкІ° мӢңмқҳ мһ‘м—…м„ұмқ„ кі л Өн•ҳм—¬ ліјнҠё мӨ„кё° м§ҒкІҪліҙлӢӨ м•Ҫк°„ нҒ¬кІҢ м—¬мң лҘј л‘җлҠ”лҚ°, мқҙ н•ҙм„қм—җм„ңлҠ” 21 mmлЎң м„Өм •н•ҳмҳҖлӢӨ.
мң н•ңмҡ”мҶҢлҠ” к°•нҢҗ, ліјнҠё л°Ҹ л„ҲнҠё лӘЁл‘җ ABAQUSм—җм„ң м ңкіөн•ҳлҠ” лӢӨм–‘н•ң мў…лҘҳмқҳ мҶ”лҰ¬л“ңмҡ”мҶҢ мӨ‘ C3D8Rмқ„ мӮ¬мҡ©н•ҳмҳҖлӢӨ. мқҙлҠ” 8к°ңмқҳ м Ҳм җмқ„ к°–лҠ” мңЎл©ҙмІҙ лӘЁм–‘мқҙкі , к°җм°Ём Ғ분(reduced integration)мқ„ м Ғмҡ©н•ң мҡ”мҶҢмқҙлӢӨ. к°җм°Ём Ғ분мқҖ м „лӢЁ мһ к№Җ(shear locking) нҳ„мғҒкіј к°ҷмқҖ мң н•ңмҡ”мҶҢн•ҙм„қ мӢңмқҳ л¶Җмһ‘мҡ©мқ„ л°©м§Җн• мҲҳ мһҲкі н•ҙм„қмӢңк°„мқҙ лӢЁм¶•лҗҳлҠ” мһҘм җлҸ„ мһҲлӢӨ. мҡ”мҶҢмқҳ нҸүл©ҙмғҒ н•ң ліҖ кёёмқҙлҠ” мөңлҢҖ 10 mm мқҙн•ҳлЎң 비көҗм Ғ мЎ°л°Җн•ҳкІҢ кө¬м„ұн•ҳм—¬ н•ҙмқҳ м •нҷ•м„ұмқ„ мң м§Җн•ҳмҳҖлӢӨ. н•ңнҺё нҡҢм „ мһҗмң лҸ„к°Җ м—ҶлҠ” мҶ”лҰ¬л“ңмҡ”мҶҢмқҳ лӢЁм җмқ„ ліҙмҷ„н•ҳм—¬ нңЁ кұ°лҸҷмқ„ мҳ¬л°”лЎң лӘЁмӮ¬н• мҲҳ мһҲлҸ„лЎқ к°•нҢҗ л‘җк»ҳ л°©н–ҘмңјлЎңлҠ” 4к°ң мёөмңјлЎң л¶„н• н•ҳмҳҖлӢӨ.
мғҒн•ҳ нҢҢнҳ•к°•нҢҗ мӮ¬мқҙмқҳ м ‘мҙүл©ҙ, к·ёлҰ¬кі к°•нҢҗкіј ліјнҠё л°Ҹ л„ҲнҠёк°Җ м„ңлЎң м ‘мҙүн•ҳлҠ” кұ°лҸҷмқ„ кө¬нҳ„н•ҳкё° мң„н•ҙ ABAQUSмқҳ лӢӨм–‘н•ң м ‘мҙү н•ҙм„қ лӘЁлҚёл§Ғ л°©лІ• мӨ‘м—җм„ң general contact кё°лҠҘмқ„ м Ғмҡ©н•ҳмҳҖлӢӨ. м ‘мҙү н•ҙм„қм—җм„ңлҠ” м ‘мҙүл©ҙ к°„мқҳ м ‘м„ л°©н–Ҙ л§Ҳм°° кұ°лҸҷм—җ лҢҖн•ң лӘЁлҚёл§ҒлҸ„ к°ҖлҠҘн•ңлҚ°, мқҙ м—°кө¬м—җм„ңлҠ” Fig. 6(b)мҷҖ к°ҷмқҙ мғҒн•ҳ нҢҢнҳ•к°•нҢҗ мӮ¬мқҙм—җ лҒјмӣҢ л„Јм–ҙ м••м°©лҗҳлҠ” мң м—°н•ң мһ¬м§Ҳмқҳ к°ңмҠӨнӮ·мқҳ мҳҒн–Ҙмқ„ кі л Өн•ҳм—¬ л§Ҳм°°мқҙ м—ҶлҠ” мЎ°кұҙмңјлЎң ліҙм•ҳлӢӨ. мҰү, к°ңмҠӨнӮ·мқ„ м§Ғм ‘ лӘЁлҚёл§Ғн•ҳм§Җ м•Ҡкі к·ё мҳҒн–Ҙмқ„ к°„м ‘м ҒмңјлЎң кі л Өн•ҳмҳҖлӢӨ.
Fig. 8кіј к°ҷмқҙ н•ҳмӨ‘мңјлЎңлҠ” 3.3м Ҳм—җм„ң м–ёкёүн• м¶•л Ҙкіј нңЁлӘЁл©ҳнҠёлҘј мһ‘мҡ©мӢңмј°мңјл©°, кІҪкі„мЎ°кұҙмңјлЎң н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳлҠ” мёЎл©ҙмқҖ мһҗмң лЎңмҡҙ ліҖмң„лҘј н—Ҳмҡ©н•ҳмҳҖкі , н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳлҠ” м•ҠлҠ” мёЎл©ҙмқҖ ліҖнҳ• мӢң кө¬мҶҚмқ„ мөңмҶҢнҷ”н•ҳм—¬ мӢӨм ң кө¬мЎ°л¬јкіј мң мӮ¬н•ҳкІҢ кұ°лҸҷн• мҲҳ мһҲлҸ„лЎқ н•ҳмҳҖлӢӨ. мҰү, Fig. 8м—җм„ң мқҢмҳҒ н‘ңмӢңлҗң мёЎл©ҙмқҳ кІҪмҡ° x л°©н–ҘмңјлЎңлҠ” кө¬мҶҚн•ҳлҗҳ, y л°Ҹ z л°©н–ҘмңјлЎңлҠ” мөңмҶҢн•ңмқҳ мң„м№ҳл§Ң кө¬мҶҚн•ҳмҳҖлӢӨ. н•ңнҺё м—ӯмӢң мӢӨм ң кұ°лҸҷмқ„ лӘЁмӮ¬н•ҳкё° мң„н•ҙ ліјнҠём—җлҠ” м–ҙл– н•ң кө¬мҶҚмЎ°кұҙлҸ„ л¶Җм—¬н•ҳм§Җ м•Ҡм•ҳлӢӨ. Fig. 8мқҖ мғҒнҢҗ л°Ҹ н•ҳнҢҗмқҙ ліјнҠё м ‘н•©мқ„ нҶөн•ҙ кІ°н•©лҗң н•ҙм„қлӘЁлҚёмқ„ ліҙм—¬мЈјкі мһҲмңјл©°, м—°лӢЁкұ°лҰ¬ л°Ҹ ліјнҠё к°„кІ©мқҳ м •мқҳлҸ„ н•Ёк»ҳ лӮҳнғҖлӮҙм—ҲлӢӨ.
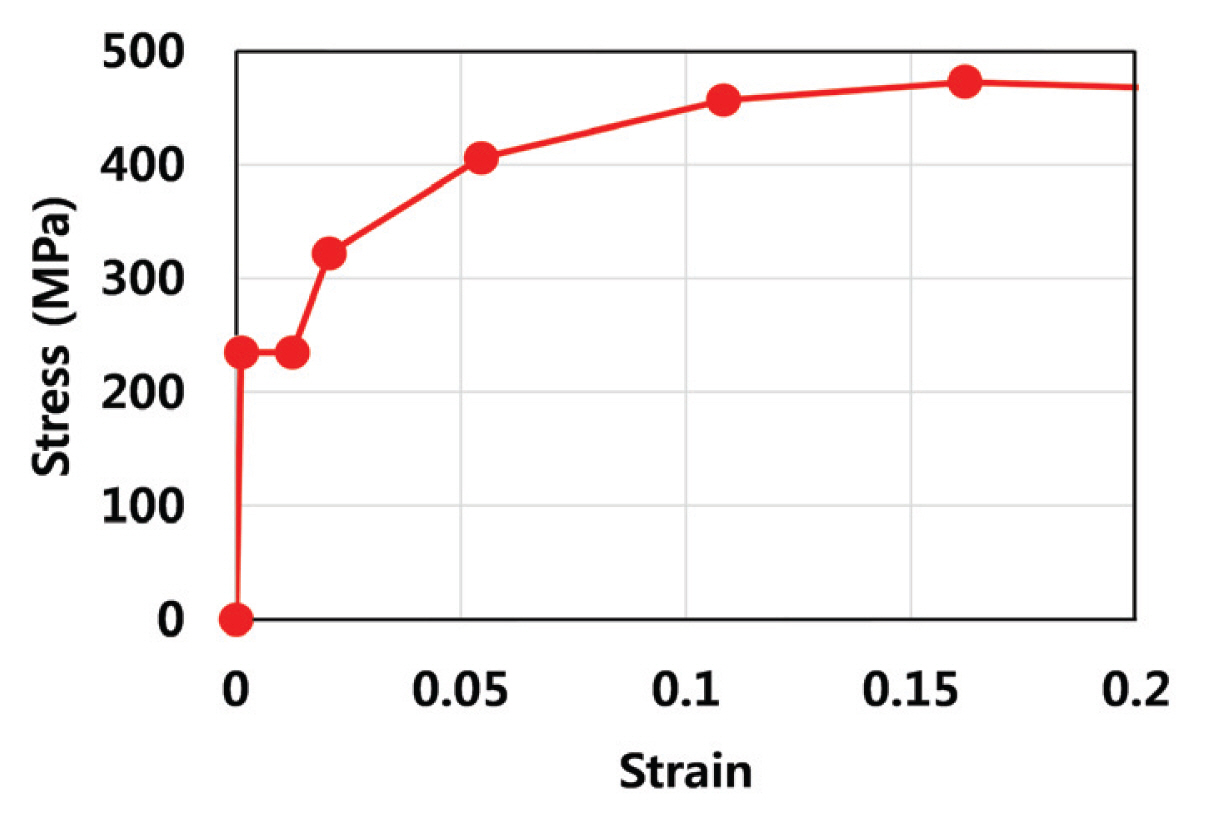
нҢҢнҳ•к°•нҢҗмқҳ мһ¬лЈҢл¬јм„ұмқҖ Fig. 9мҷҖ к°ҷмқҙ мһ¬лЈҢмқҳ л№„м„ нҳ•м„ұмқ„ л°ҳмҳҒн•ң м—„л°Җн•ң мқ‘л Ҙ-ліҖнҳ•лҘ кіЎм„ мқ„ кі л Өн•ҳмҳҖлӢӨ. н‘ңмӨҖнҳ• нҢҢнҳ•к°•нҢҗм—җлҠ” SS400мқҳ к°•мһ¬ к·ңкІ©мқҙ мӮ¬мҡ©лҗҳл©°, н•ӯліөк°•лҸ„лҠ” 235 MPa, мқёмһҘк°•лҸ„лҠ” 400 MPa, нғ„м„ұкі„мҲҳлҠ” 2.05Г—105 MPa, нҸ¬м•„мҶЎл№„лҠ” 0.3мқҙлӢӨ. к°•нҢҗмқҖ к°ҖмһҘ ліҙнҺём ҒмңјлЎң мӮ¬мҡ©лҗҳлҠ” нҸ° лҜём ңмҠӨ(von Mises)мқҳ н•ӯліөкё°мӨҖмқ„ л”°лҘҙлҠ” кІғмңјлЎң н•ҳмҳҖлӢӨ. н•ңнҺё ліјнҠёмқҳ кІҪмҡ° мқёмһҘк°•лҸ„ 800 MPaмқҳ кі мһҘл Ҙ ліјнҠёмқҙлҜҖлЎң ліјнҠём—җм„ң нҢҢлӢЁмқҙ л°ңмғқн•ҳм§ҖлҠ” м•ҠлҠ”лӢӨкі ліҙкі , нғ„м„ұкі„мҲҳ 2.05Г—105 MPaмқҳ м„ нҳ•нғ„м„ұмңјлЎң лӘЁлҚёл§Ғн•ҳмҳҖлӢӨ.
мқҙлҹ¬н•ң нҢҢнҳ•к°•нҢҗ ліјнҠё мқҙмқҢл¶Җ н•ҙм„қмқҳ кІҪмҡ° ліјнҠёмқҳ мІҙкІ°м—җ лҢҖн•ң лӘЁлҚёл§Ғмқҙ н•ҙм„қ кІ°кіјм—җ мӨ‘мҡ”н•ң мҳҒн–Ҙмқ„ лҜём№ңлӢӨ. кё°мЎҙ м—°кө¬лҘј мӮҙнҺҙліҙл©ҙ ліјнҠё мІҙкІ°л Ҙмқҳ мҳҒн–Ҙмқҙ нҒ¬м§Җ м•ҠлӢӨкі ліҙкі мқҙлҘј л¬ҙмӢңн•ҳкі н•ҙм„қн•ң кІҪмҡ°к°Җ мһҲлӢӨ(Kang, 2004; Lee, 2012). н•ҳм§Җл§Ң мқҙл•Ңм—җлҠ” ліјнҠёмқҳ мІҙкІ°м—җ мқҳн•ҙ к°•нҢҗ л‘җк»ҳ л°©н–ҘмңјлЎң мһ‘мҡ©н•ҳлҠ” 압축мқ‘л Ҙмқҙ кі л Өлҗҳм§Җ м•Ҡм•„ мҳ¬л°”лҘё мқ‘л Ҙ мғҒнғңлҘј лӘЁмӮ¬н• мҲҳ м—ҶлҠ” нҒ° лӢЁм җмқҙ мһҲмңјлҜҖлЎң ліјнҠё мІҙкІ°л ҘмқҖ кі л Өлҗҳм–ҙм•ј н•ңлӢӨ. лҳҗн•ң ліјнҠёмқҳ мІҙкІ°мқ„ лӘЁлҚёл§Ғн•ҳм§Җ м•Ҡмңјл©ҙ, мғҒнҢҗ, н•ҳнҢҗ, ліјнҠё л°Ҹ л„ҲнҠёк°Җ м„ңлЎң кІ°н•©лҗҳм§Җ м•ҠмқҖ кө¬мЎ°м ҒмңјлЎң л¶Ҳм•Ҳм •н•ң мғҒнғңк°Җ лҗҳлҜҖлЎң мӢӨм ңмҷҖлҠ” лӢӨлҘё 추к°Җм Ғмқё кө¬мҶҚмЎ°кұҙмқҙ н•„мҡ”н•ҳлӢӨ. н•ңнҺё ліјнҠём—җ мІҙкІ°л Ҙмқҙ мһ‘мҡ©н• л•Ң м•Ҳм •м Ғмқё н•ҙм„қмқ„ мң„н•ҙ ліјнҠёмқҳ нҠ№м • мң„м№ҳм—җ мӢӨм ңмҷҖ лӢӨлҘё кө¬мҶҚмЎ°кұҙмқ„ л¶Җм—¬н•ҙлҸ„ м•Ҳ лҗңлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” мӢӨм ңмҷҖ к°ҖмһҘ мң мӮ¬н•ң мғҒнҷ©мқҙ лӘЁмӮ¬лҗ мҲҳ мһҲлҸ„лЎқ мҙҲкё°мқ‘л Ҙ(initial stress)мқ„ ліјнҠём—җ к°Җн•ҳм—¬ ліјнҠё 축л Ҙ, мҰү, ліјнҠё мІҙкІ°л Ҙмқ„ кө¬нҳ„н•ҳмҳҖлӢӨ. н•ҙм„қмқҖ 1м°Ём ҒмңјлЎң ліјнҠё мІҙкІ°мқ„ нҶөн•ҙ ліјнҠё мқҙмқҢл¶Җмқҳ 2к°ң нҢҢнҳ•к°•нҢҗмқҙ кІ°н•©лҗҳкі , мқҙл ҮкІҢ кІ°н•©лҗң нҢҢнҳ•к°•нҢҗм—җ 추к°Җм ҒмңјлЎң 압축л ҘмқҙлӮҳ нңЁлӘЁл©ҳнҠёк°Җ к°Җн•ҙм§ҖлҠ” лӢЁкі„лі„ н•ҙм„қмқ„ мҲҳн–үн•ҳмҳҖлӢӨ. мқҙл•Ң ліјнҠё мІҙкІ°л ҘмқҖ нӣ„мҶҚ н•ҳмӨ‘мқҙ к°Җн•ҙм§Ҳ л•Ңм—җлҸ„ мҳ¬л°”лЎң мң м§Җлҗҳкі мһҲмқҢмқ„ нҷ•мқён•ҳмҳҖлӢӨ.
мӢӨм ң мӢңкіө мӢң м°ёмЎ°лҗҳлҠ” н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ёмқҳ ліјнҠё мЎ°мһ„ нҶ нҒ¬ лІ”мң„мқё 200вҲј400 NВ·mлҘј ліјнҠё 축л ҘмңјлЎң ліҖнҷҳн•ҳкё° мң„н•ҙм„ң нҶөмғҒм ҒмңјлЎң мӮ¬мҡ©н•ҳлҠ” Eq. (1)(Han et al., 2008) л°Ҹ Eq. (2)(Sindo ILS, 2018)лҘј м Ғмҡ©н•ҳмҳҖлӢӨ. мқҙлҹ¬н•ң мҲҳмӢқмңјлЎң кІҖнҶ н•ҙ ліҙл©ҙ нҢҢнҳ•к°•нҢҗ ліјнҠёмқҳ мІҙкІ°л ҘмқҖ 60вҲј120 kN лІ”мң„мқҙл©°, мқҙ н•ҙм„қм—җ мӮ¬мҡ©лҗң 20 mm м§ҒкІҪ ліјнҠёмқҳ лӢЁл©ҙм ҒмңјлЎң лӮҳлҲ„м–ҙ мқ‘л ҘмңјлЎң нҷҳмӮ°н•ҙ ліҙл©ҙ 191вҲј382 MPaмқҙ мӮ°м¶ңлҗңлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” мқҙлҹ¬н•ң лІ”мң„мқҳ нҸүк· к°’ліҙлӢӨ м•Ҫк°„ мһ‘мқҖ 240 MPaмқҳ мҙҲкё°мқ‘л Ҙмқ„ ліјнҠём—җ лҸ„мһ…н•ҳмҳҖлӢӨ.
м—¬кё°м„ң, T: нҶ нҒ¬, K: нҶ нҒ¬ кі„мҲҳк°’(Type A: 0.11вҲј0.15, Type B: 0.15вҲј0.19, мқҙ н•ҙм„қм—җм„ңлҠ” Type B мӮ¬мҡ©), d: ліјнҠё мҷёкІҪ, N: ліјнҠё мЎ°мһ„ 축л Ҙ.
м—¬кё°м„ң, T: нҶ нҒ¬, Ki: 0.75вҲј0.9(л°ҳліөмІҙкІ°: 0.75, мҳҒкө¬мІҙкІ°: 0.9), As: ліјнҠё мң нҡЁлӢЁл©ҙм Ғ, SP: ліјнҠё ліҙмҰқк°•лҸ„(н•ӯліөк°•лҸ„ мқҙн•ҳмқҙл©°, мқјл°ҳм ҒмңјлЎң н•ӯліөк°•лҸ„мқҳ 90%).
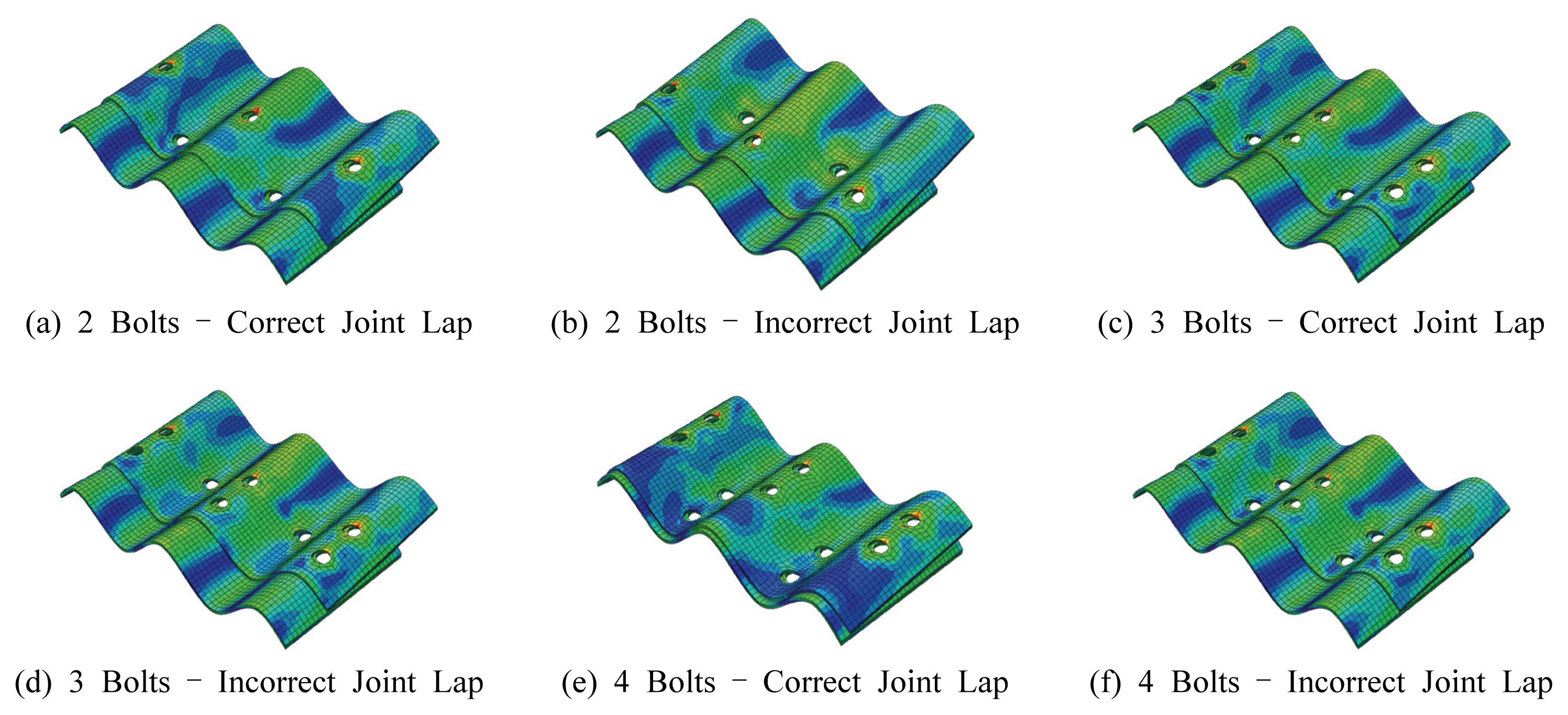
н•ҙм„қ ліҖмҲҳлҠ” Table 1кіј к°ҷмқҙ н”јм№ҳлӢ№ ліјнҠё к°ңмҲҳ, ліјнҠё л°°м—ҙ, н•ҳмӨ‘, м—°лӢЁкұ°лҰ¬, ліјнҠё к°„кІ©мқҙлӢӨ. ліјнҠё к°ңмҲҳлҠ” нҶөмғҒм Ғмқё 2ліјнҠё мқҙмҷём—җ 3ліјнҠё л°Ҹ 4ліјнҠём—җ лҢҖн•ҙм„ңлҸ„ кІҖнҶ н•ҳмҳҖкі , ліјнҠё л°°м—ҙмқҖ м •л°°м—ҙ л°Ҹ л¶Җл°°м—ҙмқ„ кі л Өн•ҳмҳҖлӢӨ. Table 2лҠ” 2, 3, 4ліјнҠё мӢңмҠӨн…ң к°Ғк°Ғм—җ лҢҖн•ҳм—¬ м •л°°м—ҙ л°Ҹ л¶Җл°°м—ҙлЎң ліјнҠёк°Җ л°°м№ҳлҗң мң н•ңмҡ”мҶҢ лӘЁлҚёмқ„ ліҙм—¬мЈјкі мһҲмңјл©°, кө¬л¶„мқ„ мң„н•ҙ мғҒнҢҗмқҖ м§ҷмқҖ мғүмңјлЎң, н•ҳнҢҗмқҖ мҳ…мқҖ мғүмңјлЎң н‘ңнҳ„н•ҳмҳҖлӢӨ.
кё°мЎҙмқҳ н•ҙм„қм Ғ м—°кө¬(Kang, 2004; Lee, 2012)м—җм„ңлҠ” 압축л Ҙл§Ңмқ„ кІҖнҶ н•ҳкі , нңЁлӘЁл©ҳнҠёлҠ” кі л Өн•ҳм§Җ м•Ҡм•ҳмңјлҜҖлЎң мӢӨм ң ліјнҠё мқҙмқҢл¶Җ м—ҙнҷ”мқҳ мЈјлҗң мӣҗмқёмңјлЎң м•Ңл Ө진 нңЁлӘЁл©ҳнҠёмқҳ мҳҒн–Ҙмқҙ 분м„қлҗҳм§Җ лӘ»н–Ҳм—ҲлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” кё°мЎҙ м—°кө¬мқҳ лӢЁм җмқ„ к°ңм„ н•ҳм—¬ 압축л Ҙ л°Ҹ нңЁлӘЁл©ҳнҠёмқҳ к°ңлі„м Ғмқё мҳҒн–Ҙ л°Ҹ ліөн•©м Ғмқё мҳҒн–Ҙмқ„ лҸҷмӢңм—җ 분м„қн•ҙ ліҙм•ҳмңјл©°, мӢӨм ң кө¬мЎ°л¬јмқҳ мқ‘л Ҙ л°ңмғқ мҲҳмӨҖмқ„ мҳҲмёЎн•ҳкё° мң„н•ҙ кё°мЎҙ мһҗлЈҢ 분м„қмқ„ нҶөн•ҙ мӢӨм ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җ л°ңмғқн–Ҳкұ°лӮҳ л°ңмғқн•ң кІғмңјлЎң мҳҲмёЎлҗҳлҠ” н•ҳмӨ‘к°’мқ„ м Ғмҡ©н•ҳмҳҖлӢӨ(Daewoo E&C and Ajou University, 2017). 압축л ҘмқҖ мӢңкіө мӮ¬лЎҖ 분м„қмқ„ нҶөн•ҙ 비көҗм Ғ л‘җкәјмҡҙ нҶ н”јлҘј к°Җ진 кІҪмҡ° л°ңмғқн• мҲҳ мһҲлҠ” к°’мқ„ кі л Өн•ҳмҳҖлӢӨ. мқҙл•Ң мғҒмһ¬нҶ м••мқ„ нҢҢнҳ•к°•нҢҗ 압축л ҘмңјлЎң ліҖнҷҳн•ҳкё° мң„н•ҙм„ң кұ°мқҳ лӘЁл“ кҙҖл Ё м„Өкі„кё°мӨҖ(KEC, 2001; AISI, 2002; CSA, 2006)м—җм„ң мұ„нғқн•ҳкі мһҲлҠ” Eq. (3)кіј к°ҷмқҖ 압축л§Ғ мқҙлЎ мқ„ м Ғмҡ©н•ҳмҳҖлӢӨ. лӢӨл§Ң м„Өкі„кё°мӨҖм—җ л”°лқј м•„м№ӯ нҡЁкіјмқҳ кі л Ө м—¬л¶Җ л°Ҹ л°©лІ•м—җ мһҲм–ҙм„ңлҠ” м°Ёмқҙк°Җ мһҲм§Җл§Ң м—¬кё°м—җм„ңлҠ” н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ём—җ л”°лқј м•„м№ӯ нҡЁкіјлҘј кі л Өн•ҳм§Җ м•Ҡм•ҳлӢӨ. мқҙлҹ¬н•ң 압축л ҘмқҖ 압축мқ‘л ҘмңјлЎң ліҖнҷҳн•ҳм—¬ к°•нҢҗ мёЎл©ҙм—җ к°Җн•ҳмҳҖлӢӨ. лҳҗн•ң нңЁлӘЁл©ҳнҠёмқҳ кІҪмҡ° н•ңкөӯлҸ„лЎңкіөмӮ¬м—җм„ң 3D 진лӢЁ лЎңлҙҮ л°Ҹ л§өн•‘ кё°лІ•мқ„ м Ғмҡ©н•ҳм—¬ к°ңл°ңн•ң ARGOS мӢңмҠӨн…ң(Lee et al., 2014)мқ„ нҶөн•ҳм—¬ көӯлӮҙ нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јл“Өм—җм„ң мӢӨмёЎн•ң лӮҙкіөліҖмң„м—җ к·јкұ°н•ҳм—¬ кі„мӮ°н•ң нңЁлӘЁл©ҳнҠё лҚ°мқҙн„° мӨ‘ м•Ҳм „мёЎмңјлЎң нҒ° к°’мқ„ м·Ён•ҳмҳҖлӢӨ. мқҙл•Ң нңЁлӘЁл©ҳнҠёлҠ” Eq. (4)лҘј нҶөн•ҳм—¬ мӮ°м •н•ҳкІҢ лҗңлӢӨ. мқҙлҹ¬н•ң нңЁлӘЁл©ҳнҠёмҷҖ лҸҷл“ұн•ң нҡЁкіјлҘј л°ңмғқмӢңнӮӨлҸ„лЎқ к°•нҢҗ мёЎл©ҙм—җ мқёмһҘ л°Ҹ 압축мқҳ 집мӨ‘н•ҳмӨ‘мқ„ м Ғм ҲнһҲ к°Җн•ҳмҳҖлӢӨ.
м—¬кё°м„ң, T: 압축л Ҙ, Pv: мғҒмһ¬ н•ҳмӨ‘, S: к°•нҢҗ нҸӯ, Оі: мғҒмһ¬нҶ мқҳ лӢЁмң„мӨ‘лҹү, H: нҶ н”ј.
м—¬кё°м„ң, M: нңЁлӘЁл©ҳнҠё, Ec: нҢҢнҳ•к°•нҢҗ нғ„м„ұкі„мҲҳ, Ic: нҢҢнҳ•к°•нҢҗ лӢЁл©ҙ2м°ЁлӘЁл©ҳнҠё, R: кіЎлҘ л°ҳкІҪ м„Өкі„к°’, RN: ліҖнҳ• нӣ„мқҳ кіЎлҘ л°ҳкІҪ.
н•ңнҺё м—°лӢЁкұ°лҰ¬ л°Ҹ ліјнҠё к°„кІ©м—җ лҢҖн•ҙм„ңлҸ„ ліҖмҲҳ н•ҙм„қмқ„ мӢӨмӢңн•ҳмҳҖмңјл©°, м—°лӢЁкұ°лҰ¬лҠ” н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ём—җ м ңмӢңлҗң 35 mmлҘј кё°мӨҖмңјлЎң 20 mm, 50 mm л°Ҹ 65 mmлЎң ліҖнҷ”мӢңмјң к°Җл©ҙм„ң к·ё мҳҒн–Ҙмқ„ 분м„қн•ҳмҳҖлӢӨ. лҳҗн•ң ліјнҠё к°„кІ©мқҖ м—ӯмӢң лҸҷмқјн•ң кё°мӨҖмқҳ 50 mmлҘј кё°ліёмңјлЎң н•ҳм—¬ 20 mm, 35 mm л°Ҹ 65 mmлЎң ліҖнҷ”мӢңмј°лӢӨ.
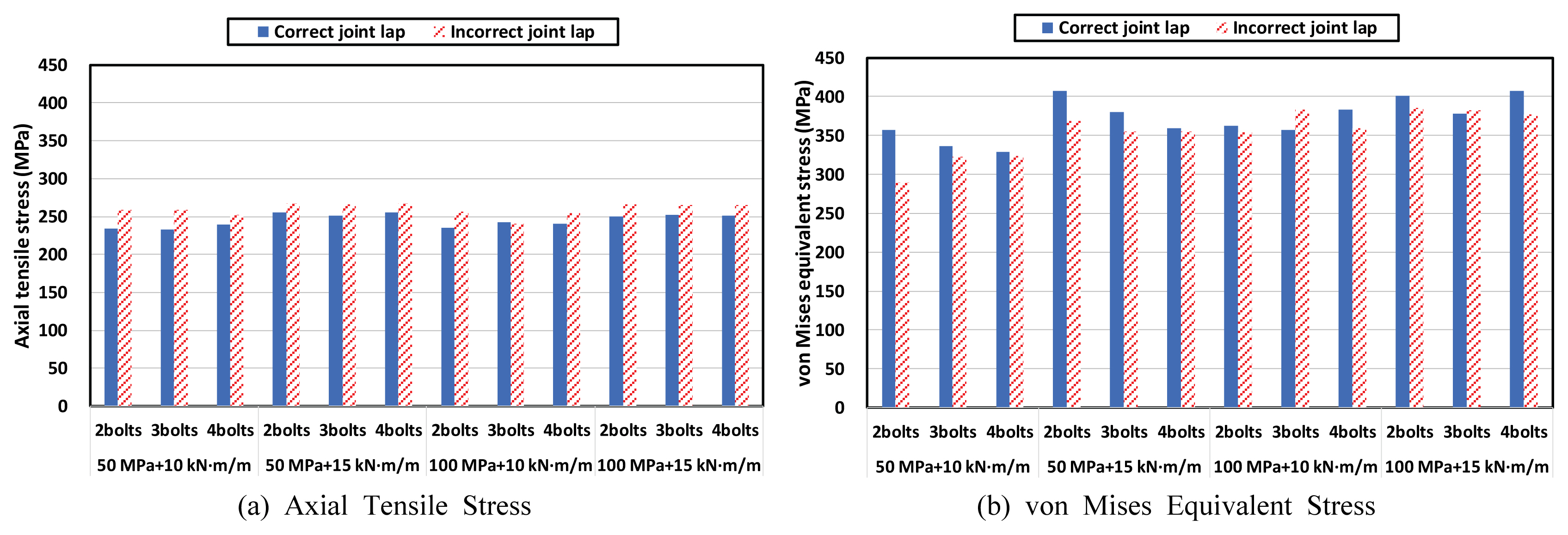
ліјнҠё мІҙкІ°л Ҙ, 압축л Ҙ л°Ҹ нңЁлӘЁл©ҳнҠёлҘј лӢЁкі„лі„лЎң мһ‘мҡ©мӢңмј°мқ„ л•Ң ліјнҠё к°ңмҲҳ л°Ҹ ліјнҠё л°°м—ҙм—җ л”°лҘё ліҖнҳ• нҳ•мғҒ л°Ҹ мқ‘л Ҙ 분нҸ¬лҠ” Fig. 10кіј к°ҷмңјл©°, ліјнҠёліҙлӢӨлҠ” к°•нҢҗмқҳ мқ‘л Ҙмқҙ мЈјмҡ” 분м„қлҢҖмғҒмқҙлҜҖлЎң к°•нҢҗмқҳ мқ‘л Ҙл§Ңмқ„ лӮҳнғҖлӮҙм—ҲлӢӨ. мқҙлҠ” Table 1м—җм„ң лҢҖн‘ңм ҒмңјлЎң 7, 8, 15, 16, 23, 24м—җ лҢҖн•ң н•ҙм„қ кІ°кіјлҘј ліҙм—¬мӨҖ кІғмқҙлӢӨ.
Fig. 10мқҳ ліҖнҳ• нҳ•мғҒмқҖ кө¬л¶„мқ„ мң„н•ҳм—¬ мӢӨм ңмқҳ ліҖнҳ•мқ„ 10л°° мҰқнҸӯн•ҳм—¬ лӮҳнғҖлӮҙм—ҲлӢӨ. ліјнҠё к°ңмҲҳк°Җ мҰқк°Җн• мҲҳлЎқ мғҒнҢҗ л°Ҹ н•ҳнҢҗмқҳ мқјмІҙм„ұмқҙ мҰқлҢҖлҗң мғҒнғңлЎң мҷёл Ҙм—җ м Җн•ӯн• мҲҳ мһҲмңјлҜҖлЎң к°•нҢҗмқҳ ліҖнҳ•мқҙ к°җмҶҢн•ҳлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ. лҳҗн•ң л¶Җл°°м—ҙліҙлӢӨ м •л°°м—ҙм—җм„ң к°•нҢҗмқҳ ліҖнҳ•мқҙ мһ‘кІҢ л°ңмғқн•ҳмҳҖлҠ”лҚ°, мқҙлҠ” кё°мЎҙм—җ м ңм•Ҳлҗң Fig. 4мҷҖ к°ҷмқҖ кұ°лҸҷмқҙ м–ҙлҠҗм •лҸ„ мң нҡЁн•Ёмқ„ мқҳлҜён•ңлӢӨ.
н•ңнҺё мқ‘л Ҙмқҳ кІҪмҡ° Eq. (5)мҷҖ к°ҷмқҖ нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙ(von Mises equivalent stress)мңјлЎң 분м„қн•ҙ ліҙм•ҳлӢӨ. мқҙлҠ” нҸ° лҜём ңмҠӨ н•ӯліөкё°мӨҖм—җ к·јкұ°н•ҳм—¬ мӢӨм ңмқҳ лӢӨ축 мқ‘л ҘмғҒнғңлҘј мқјм¶•мқҳ мқ‘л Ҙ-ліҖнҳ•лҘ кіЎм„ кіј мң мӮ¬н•ҳкІҢ н‘ңнҳ„н•ң кІғмқҙлӢӨ. мҳҲлҘј л“Өм–ҙ мқҙ к°’мқҙ к°•нҢҗмқҳ н•ӯліөк°•лҸ„кіј мң мӮ¬н•ҳл©ҙ 3м°Ёмӣҗ нҸ° лҜём ңмҠӨ н•ӯліөкё°мӨҖмғҒмқҳ н•ӯліө мӢңм җм—җ лҸ„лӢ¬н–ҲмқҢмқ„ мқҳлҜён•ңлӢӨ. н•ӯліө мқҙнӣ„м—җлҸ„ мқёмһҘк°•лҸ„м—җ лӢӨлӢӨлҘј л•Ңк№Ңм§ҖлҠ” ліҖнҳ•лҘ кІҪнҷ” нҳ„мғҒм—җ мқҳн•ҙ нҸ° лҜём ңмҠӨ н•ӯліөкё°мӨҖ лҳҗлҠ” нҢҢкҙҙнҸ¬лқҪм„ мқҙ нҷ•мһҘлҗҳкі нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘлҸ„ мҰқк°Җн•ҳкІҢ лҗңлӢӨ.
м—¬кё°м„ң, ПғvлҠ” нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙмқҙкі , Пғ i j '
н•ҳмӨ‘ лӢЁкі„м—җ л”°лҘё мқ‘л Ҙмқҳ 분нҸ¬лҠ” Fig. 11кіј к°ҷмңјл©°, лҢҖн‘ңм ҒмңјлЎң Table 1мқҳ 7 л°Ҹ 8м—җ н•ҙлӢ№лҗҳлҠ” 2ліјнҠё м •л°°м—ҙм—җм„ң мғҒнҢҗмқҳ мғҒл©ҙ мқ‘л Ҙ 분нҸ¬лҘј ліјнҠёлҘј м ңмҷён•ҳкі лӮҳнғҖлӮҙм—ҲлӢӨ. нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘмңјлЎң кІҖнҶ н•ң кІ°кіј мқҙлҜё ліјнҠё мІҙкІ° мӢң ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗм—җм„ң ліјнҠё лЁёлҰ¬ лҳҗлҠ” л„ҲнҠёмҷҖ л§һлӢҝлҠ” көӯл¶Җм Ғмқё л¶Җ분мқҙ н•ӯліөк°•лҸ„ к°Җк№Ңмқҙ лҸ„лӢ¬лҗЁмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ. мқҙлҠ” кіЎл©ҙ нҳ•мғҒмқҳ нҢҢнҳ•к°•нҢҗмқ„ ліјнҠёлЎң мІҙкІ°н•ҳлҠ” кіјм •м—җм„ң ліјнҠё лЁёлҰ¬ лҳҗлҠ” л„ҲнҠёмҷҖ к°•нҢҗмқҙ көӯл¶Җм ҒмңјлЎң м ‘мҙүн•ҳлҠ” л¶Җмң„м—җ мқ‘л Ҙмқҙ 집мӨ‘лҗҳкё° л•Ңл¬ёмңјлЎң нҢҗлӢЁлҗңлӢӨ. лҳҗн•ң 압축л Ҙкіј нңЁлӘЁл©ҳнҠёк°Җ 추к°ҖлЎң мһ‘мҡ©лҗҳл©ҙ мқҙлҹ¬н•ң ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗмқҳ көӯл¶Җ мқ‘л Ҙмқҙ н•ӯліөк°•лҸ„ мқҙмғҒмңјлЎң лҚ”мҡұ мҰқк°Җн•ҳкІҢ лҗңлӢӨ. лӢӨл§Ң мқҙ н•ҙм„қ кІ°кіјлҠ” мӢӨм ңлЎң мһ‘мҡ©н• к°ҖлҠҘм„ұмқҙ мһҲлҠ” 압축л ҘмқҙлӮҳ нңЁлӘЁл©ҳнҠё мӨ‘ к°ҖмһҘ лҶ’мқҖ мҲҳмӨҖмқҳ нҒ¬кё°лҘј к°Җм •н•ң кІғмңјлЎңм„ң, л°ңмғқ к°ҖлҠҘн•ң к°ҖмһҘ л¶ҲлҰ¬н•ң мқ‘л Ҙ мғҒнғңлЎң ліј мҲҳ мһҲмңјл©° мқјл°ҳм ҒмңјлЎңлҠ” мқҙліҙлӢӨ мһ‘мқҖ мҲҳмӨҖмқҳ мқ‘л Ҙмқҙ л°ңмғқн• кІғмңјлЎң мҳҲмёЎлҗңлӢӨ.
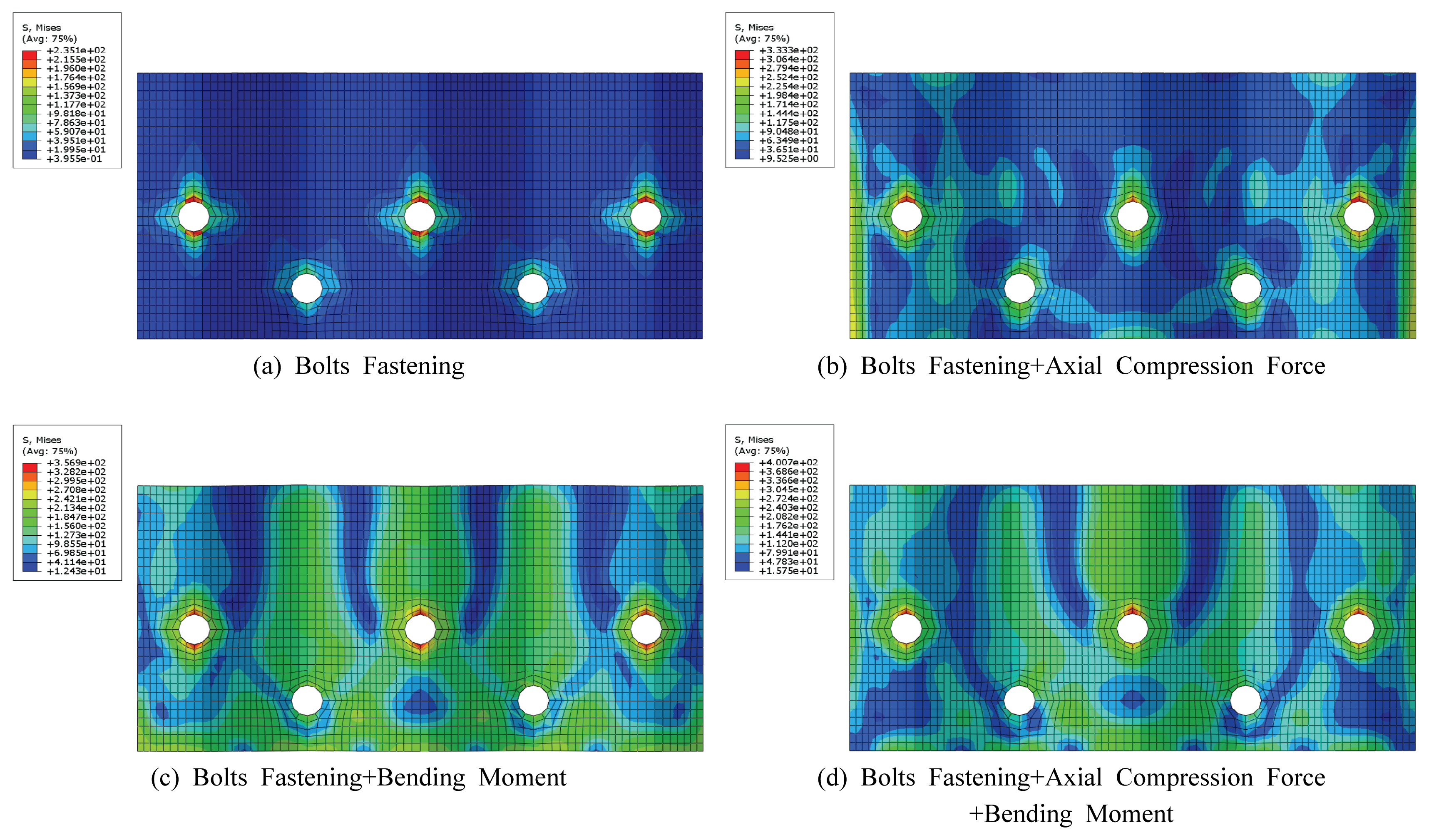
ліјнҠёлЎң мІҙкІ°лҗң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җ 압축л Ҙл§Ң мһ‘мҡ©н•ҳлҠ” кІҪмҡ°мқҳ н•ҙм„қ кІ°кіјлҘј Fig. 12м—җ лӮҳнғҖлӮҙм—ҲлӢӨ. м—¬кё°м—җм„ңлҠ” нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙ мҷём—җлҸ„ Fig. 2мҷҖ к°ҷмқҙ мӢӨм ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җм„ң кҙҖм°°лҗҳлҠ” нҳ•нғңмқҳ к· м—ҙкіј мўҖ лҚ” м§Ғм ‘м ҒмңјлЎң кҙҖл Ёлҗң 축방н–Ҙ мөңлҢҖ мқёмһҘмқ‘л Ҙмқ„ кІҖнҶ н•ҙ ліҙм•ҳлӢӨ. мөңлҢҖ мқ‘л ҘмқҖ ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗм—җм„ң л°ңмғқн•ҳмҳҖлӢӨ.
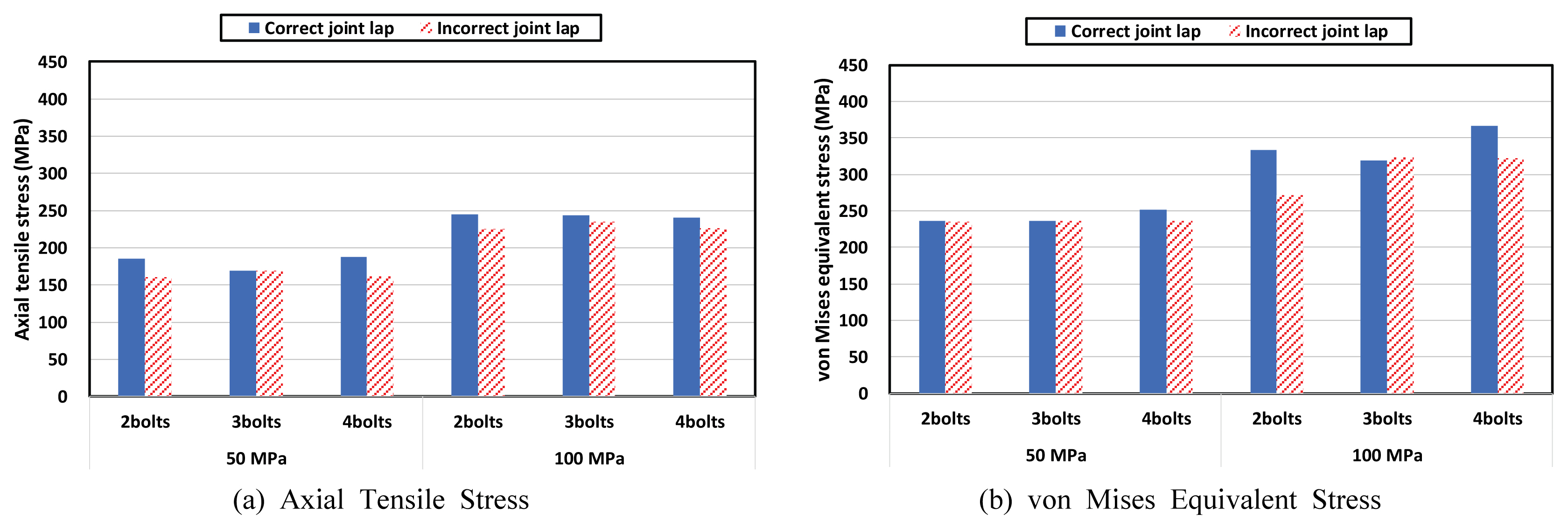
축방н–Ҙ мқ‘л Ҙмқҳ кІҪмҡ° 압축мқ‘л ҘмңјлЎң к°Җн•ҙ진 압축л Ҙмқҙ мһ‘мқҖ кІҪмҡ°м—җ 비н•ҙ нҒҙ л•Ңм—җ к°•нҢҗ мқёмһҘмқ‘л Ҙмқҙ лҚ” нҒ¬кІҢ л°ңмғқн•ҳлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬мңјлӮҳ, ліјнҠё к°ңмҲҳлӮҳ л°°м—ҙм—җ л”°лҘё мқёмһҘмқ‘л Ҙ м°ЁмқҙлҠ” нҒ¬м§Җ м•Ҡм•ҳлӢӨ. ліјнҠёл§ҲлӢӨ 축방н–Ҙ н•ҳмӨ‘мқ„ 분лӢҙн•ҳлҜҖлЎң ліјнҠё к°ңмҲҳк°Җ мҰқк°Җн• мҲҳлЎқ ліјнҠё мЈјліҖ к°•нҢҗмқҳ мқ‘л ҘлҸ„ мһ‘м•„м§Ҳ кІғмңјлЎң мҳҲмғҒн–ҲмңјлӮҳ к·ёлҹ¬н•ң кІҪн–Ҙмқҙ лӘ…нҷ•м№ҳ м•Ҡм•ҳлӢӨ. мқҙлҠ” 압축л Ҙмқҙ мһ‘мҡ©н• л•Ң көӯл¶Җм ҒмңјлЎң нҒ¬кІҢ л°ңмғқн•ҳлҠ” мқ‘л ҘмқҖ ліјнҠё к°ңмҲҳм—җ нҒ° мҳҒн–Ҙмқ„ л°ӣм§Җ м•ҠмқҢмқ„ мқҳлҜён•ҳкі мһҲлӢӨ. лҳҗн•ң мӣҗлһҳ ліјнҠё м •л°°м—ҙкіј л¶Җл°°м—ҙмқҖ Fig. 4мҷҖ к°ҷмқҙ нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н• л•Ңмқҳ кұ°лҸҷ м°ЁмқҙмҷҖ кҙҖл Ёлҗҳм§Җл§Ң, 압축л Ҙ мһ‘мҡ© мӢңм—җлҸ„ лӢӨмҶҢмқҳ мқ‘л Ҙ м°Ёмқҙк°Җ л°ңмғқн–Ҳмңјл©° мқҙл•Ңм—җлҠ” мҳӨнһҲл Ө л¶Җл°°м—ҙм—җ 비н•ҙ м •л°°м—ҙм—җм„ң мқ‘л Ҙмқҙ м•Ҫк°„ лҚ” нҒ° кІҪмҡ°к°Җ л§Һм•ҳлӢӨ. 100 MPaмқҳ 압축мқ‘л Ҙмқҙ мһ‘мҡ©н• л•Ңм—җлҠ” н•ӯліөк°•лҸ„мқё 235 MPaк№Ңм§Җ лҸ„лӢ¬н•ҳлҜҖлЎң ліјнҠё кө¬л©Қ мЈјмң„ к°•нҢҗмқҙ к· м—ҙм—җ лҢҖн•ҙ м·Ём•Ҫн•ҙм§Ҳ к°ҖлҠҘм„ұмқҙ мһҲлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ. л¬јлЎ Fig. 9мқҳ к°•нҢҗ мқ‘л Ҙ-ліҖнҳ•лҘ кіЎм„ мқ„ м°ёмЎ°н• л•Ң н•ӯліөк°•лҸ„м—җ лҸ„лӢ¬н–ҲлӢӨлҠ” мӮ¬мӢӨ мһҗмІҙк°Җ к°•нҢҗмқҳ к· м—ҙмқ„ мқҳлҜён•ҳлҠ” кІғмқҖ м•„лӢҲм§Җл§Ң, м Ғм–ҙлҸ„ к· м—ҙ л°ңмғқ к°ҖлҠҘм„ұмқҙ м»Ө진лӢӨкі ліј мҲҳ мһҲлӢӨ. н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ё(KEC, 2001)м—җ м ңмӢңлҗң мқҙмқҢл¶Җ к°•лҸ„ мӨ‘ мқҙ м—°кө¬мқҳ лҢҖмғҒмқё л‘җк»ҳ 4 mmмқҳ н‘ңмӨҖнҳ• нҢҢнҳ•к°•нҢҗмқҙ 2ліјнҠёлЎң мІҙкІ°лҗҳм—Ҳмқ„ л•Ңмқҳ мқҙмқҢл¶Җ к°•лҸ„лҘј мқ‘л ҘмңјлЎң нҷҳмӮ°н•ҙліҙл©ҙ 218 MPaмқҳ 압축мқ‘л Ҙм—җ н•ҙлӢ№лҗҳлҠ”лҚ°, мқҙ н•ҙм„қм—җ л”°лҘҙл©ҙ к·ёліҙлӢӨ мһ‘мқҖ 압축мқ‘л Ҙн•ҳм—җм„ңлҸ„ көӯл¶Җм ҒмңјлЎң к°•нҢҗмқҙ н•ӯліөн• к°ҖлҠҘм„ұмқҙ мһҲлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ. л”°лқјм„ң, нҢҢнҳ•к°•нҢҗ мў…лҘҳм—җ л”°лқј м°ЁмқҙлҠ” мһҲкІ м§Җл§Ң м Ғм–ҙлҸ„ кІҖнҶ лҢҖмғҒмқҳ кІҪмҡ° нҢҢнҳ•к°•нҢҗ м„Өкі„ мӢң мқҙмқҢл¶Җ к°•лҸ„лҘј л§ҢмЎұн•ңлӢӨлҠ” кі„мӮ°л§ҢмңјлЎңлҠ” ліјнҠё мқҙмқҢл¶Җ к· м—ҙмқ„ мҷ„м „нһҲ л°©м§Җн•ҳкё° м–ҙл Өмҡё кІғмңјлЎң мғқк°ҒлҗңлӢӨ.
нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘмқҖ 축방н–Ҙ мқ‘л ҘліҙлӢӨ нҒ¬кІҢ лӮҳнғҖлӮ¬лҠ”лҚ°, 압축мқ‘л Ҙ 50 MPaм—җм„ңлҠ” нҸ° лҜём ңмҠӨмқҳ н•ӯліөкё°мӨҖм—җ лҸ„лӢ¬н•ң л¶Җ분л“Өмқҙ мһҲм—Ҳкі , 압축мқ‘л Ҙ 100 MPaм—җм„ңлҠ” мқ‘л Ҙмқҙ лҚ”мҡұ мҰқк°Җн•ҳмҳҖмңјлӮҳ к°•нҢҗмқҳ мқёмһҘк°•лҸ„к№Ңм§Җ лҸ„лӢ¬н•ҳм§ҖлҠ” лӘ»н•ҳмҳҖлӢӨ. ліјнҠё к°ңмҲҳлӮҳ м •л¶Җл°°м—ҙ м—¬л¶Җм—җ л”°лҘё кІҪн–ҘмқҖ лӘ…нҷ•м№ҳ м•Ҡм•ҳлӢӨ.
ліјнҠёлЎң мІҙкІ°лҗң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җ нңЁлӘЁл©ҳнҠёл§Ң мһ‘мҡ©н•ҳлҠ” кІҪмҡ°мқҳ н•ҙм„қ кІ°кіјлҘј Fig. 13м—җ лӮҳнғҖлӮҙм—ҲлӢӨ. 압축мқ‘л Ҙ мһ‘мҡ© мӢңмҷҖ л§Ҳм°¬к°Җм§ҖлЎң нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙ мҷём—җлҸ„ 축방н–Ҙ мөңлҢҖ мқёмһҘмқ‘л Ҙмқ„ кІҖнҶ н•ҙ ліҙм•ҳлӢӨ. м—ӯмӢң мөңлҢҖ мқ‘л ҘмқҖ ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗм—җм„ң л°ңмғқн•ҳмҳҖлӢӨ.
축방н–Ҙ мқ‘л Ҙмқҳ кІҪмҡ° к°ҖмһҘ л‘җл“ңлҹ¬м§„ нҠ№м§•мқҖ л¶Җл°°м—ҙм—җм„ңмқҳ мқ‘л Ҙмқҙ м •л°°м—ҙм—җм„ңмқҳ мқ‘л ҘліҙлӢӨ нҒ¬кІҢ л°ңмғқн•ҳмҳҖлӢӨлҠ” м җмқҙлӢӨ. лҳҗн•ң л¶Җл°°м—ҙм—җм„ңлҠ” нңЁлӘЁл©ҳнҠёмқҳ нҒ¬кё°м—җ кҙҖкі„м—Ҷмқҙ н•ӯліөк°•лҸ„ мқҙмғҒмқҳ нҒ° мқ‘л Ҙмқҙ л°ңмғқн•ң л°ҳл©ҙ м •л°°м—ҙм—җм„ңлҠ” нңЁлӘЁл©ҳнҠёк°Җ мһ‘мқҖ кІҪмҡ° н•ӯліөк°•лҸ„ м •лҸ„мқҳ мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖкі нңЁлӘЁл©ҳнҠёк°Җ нҒ° кІҪмҡ° н•ӯліөк°•лҸ„ мқҙмғҒмқҳ мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖлӢӨ. ліјнҠё к°ңмҲҳм—җ л”°лҘё мқ‘л Ҙ м°ЁмқҙлҠ” нҒ¬м§Җ м•Ҡм•ҳмңјл©°, мқҙлҠ” нңЁлӘЁл©ҳнҠёк°Җ мһ‘мҡ©н• л•Ң көӯл¶Җм ҒмңјлЎң нҒ¬кІҢ л°ңмғқн•ҳлҠ” мқ‘л ҘмқҖ ліјнҠё к°ңмҲҳм—җ нҒ° мҳҒн–Ҙмқ„ л°ӣм§Җ м•ҠмқҢмқ„ мқҳлҜён•ңлӢӨ.
нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘмқҖ 축방н–Ҙ мқ‘л ҘліҙлӢӨ лҢҖмІҙлЎң нҒ¬кІҢ лӮҳнғҖлӮ¬лҠ”лҚ°, нҠ№м§•м Ғмқё кІғмқҖ ліјнҠё к°ңмҲҳк°Җ лҠҳм–ҙлӮЁм—җ л”°лқј мқ‘л Ҙмқҙ к°җмҶҢн•ҳлҠ” кІҪн–Ҙмқҙ 비көҗм Ғ лӘ…нҷ•нһҲ лӮҳнғҖлӮ¬лӢӨлҠ” м җмқҙлӢӨ. лҳҗн•ң нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙм—җм„ңлҠ” м •л°°м—ҙ л°Ҹ л¶Җл°°м—ҙм—җ л”°лҘё м°Ёмқҙк°Җ лӘ…нҷ•нһҲ л“ңлҹ¬лӮҳм§Җ м•Ҡм•ҳлӢӨ. нңЁлӘЁл©ҳнҠёмқҳ нҒ¬кё°м—җ л”°лҘё кІҪн–ҘмқҖ 비көҗм Ғ лҡңл ·н•ҳмҳҖлҠ”лҚ°, нңЁлӘЁл©ҳнҠё 10 kNВ·m/mмқҳ кІҪмҡ° 3ліјнҠё л°Ҹ 4ліјнҠём—җм„ңлҠ” нҸ° лҜём ңмҠӨмқҳ н•ӯліөкё°мӨҖ м •лҸ„мқҳ мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖм§Җл§Ң, 2ліјнҠём—җм„ңлҠ” н•ӯліөкё°мӨҖ мқҙмғҒмқҳ нҒ° мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖлӢӨ. л°ҳл©ҙ нңЁлӘЁл©ҳнҠё 15 kNВ·m/mмқҳ кІҪмҡ° лӘЁл“ ліјнҠё к°ңмҲҳм—җ лҢҖн•ҙ н•ӯліөкё°мӨҖмқ„ мҙҲкіјн•ң нҒ° нҒ¬кё°мқҳ мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖлӢӨ.
ліјнҠёлЎң мІҙкІ°лҗң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җ 압축л Ҙкіј нңЁлӘЁл©ҳнҠёк°Җ лҸҷмӢңм—җ мһ‘мҡ©н•ҳлҠ” кІҪмҡ°мқҳ н•ҙм„қ кІ°кіјлҘј Fig. 14м—җ лӮҳнғҖлӮҙм—Ҳмңјл©°, м—ӯмӢң мөңлҢҖ мқ‘л ҘмқҖ ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗм—җм„ң л°ңмғқн•ҳмҳҖлӢӨ.
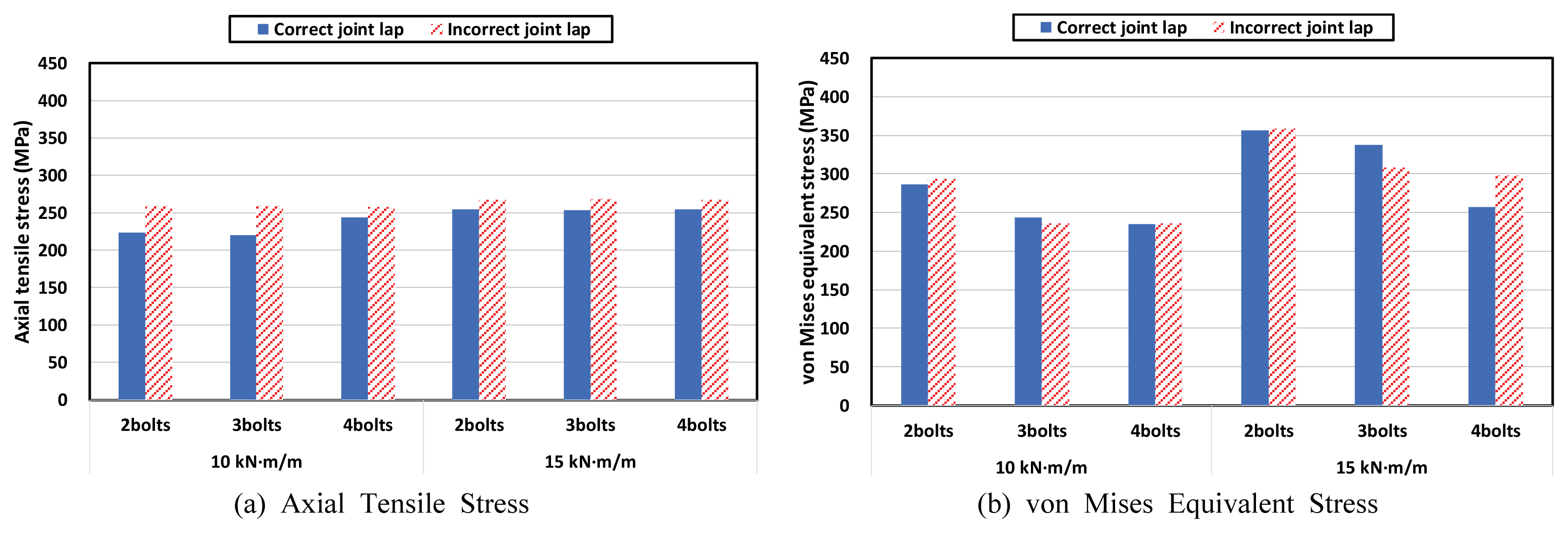
축방н–Ҙ мқ‘л Ҙмқҳ кІҪмҡ° к°ҖмһҘ л‘җл“ңлҹ¬м§„ нҠ№м§•мқҖ м •л°°м—ҙліҙлӢӨ л¶Җл°°м—ҙм—җм„ң мқ‘л Ҙмқҙ нҒ¬кІҢ л°ңмғқн•ҳмҳҖлӢӨлҠ” м җмқҙлӢӨ. мҰү, Fig. 13(a)мҷҖ к°ҷмқҙ нңЁлӘЁл©ҳнҠёл§Ң мһ‘мҡ©н•ң кІҪмҡ°м—җлҸ„ мқҙлҹ¬н•ң кІҪн–Ҙмқҙ лӮҳнғҖлӮ¬лҠ”лҚ°, 압축л Ҙк№Ңм§Җ лҸҷмӢңм—җ мһ‘мҡ©н•ҙлҸ„ мқҙлҹ¬н•ң кІҪн–Ҙмқҙ мң м§Җлҗҳм—ҲлӢӨ. мқҙлҠ” мӢӨм ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җм„ң Fig. 2мҷҖ к°ҷмқҙ м •л°°м—ҙліҙлӢӨлҠ” мЈјлЎң л¶Җл°°м—ҙ ліјнҠёмқҳ кІҪмҡ°м—җ мЈјліҖ к°•нҢҗм—җм„ң мў…л°©н–Ҙ к· м—ҙ л“ұ мҶҗмғҒмқҙ л°ңмғқн•ң кІғмңјлЎң ліҙкі лҗң кІ°кіјмҷҖ л¶Җн•©н•ңлӢӨ. м—ӯмӢң ліјнҠё кө¬л©Қ мЈјліҖ көӯл¶Җ мқ‘л ҘмқҙлҜҖлЎң ліјнҠё к°ңмҲҳм—җ л”°лҘё мқ‘л Ҙ нҒ¬кё°мқҳ кІҪн–Ҙ м°ЁмқҙлҠ” лӘ…нҷ•м№ҳ м•Ҡм•ҳлӢӨ. Fig. 2лҠ” 2ліјнҠё л¶Җл°°м—ҙ мӢңмҠӨн…ңмқҳ мҶҗмғҒ мӮ¬лЎҖлҘј ліҙм—¬мЈјкі мһҲм§Җл§Ң, лӢӨлҘё мһҗлЈҢм—җ л”°лҘҙл©ҙ 3ліјнҠё л°Ҹ 4ліјнҠё лҳҗн•ң Table 2м—җм„ң л¶Җл°°м—ҙлЎң л°°м№ҳлҗң кІҪмҡ° мң мӮ¬н•ң мҶҗмғҒмқҙ л°ңмғқн•ң мӮ¬лЎҖл“Өмқҙ ліҙкі лҗҳкі мһҲмңјл©°, мқҙ н•ҙм„қ кІ°кіјлҠ” мқҙлҹ¬н•ң мӮ¬мӢӨмқ„ л’·л°ӣм№Ён•ҳкі мһҲлӢӨ. м •л°°м—ҙм—җм„ңлҠ” н•ӯліөк°•лҸ„мқё 235 MPa мқҙн•ҳк°Җ л°ңмғқн•ң кІҪмҡ°лҸ„ м Ғм§Җ м•Ҡм•ҳм§Җл§Ң, л¶Җл°°м—ҙм—җм„ңлҠ” 압축л Ҙкіј нңЁлӘЁл©ҳнҠёк°Җ мЎ°н•©лҗң лҢҖл¶Җ분мқҳ кІҪмҡ° н•ӯліөк°•лҸ„лҘј мҙҲкіјн•ҳлҠ” мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖлӢӨ.
нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘмқҖ ліјнҠё к°ңмҲҳм—җ кҙҖкі„ м—Ҷмқҙ мқҙ кІҖнҶ м—җм„ң к°ҖмһҘ мһ‘мқҖ 압축л Ҙкіј нңЁлӘЁл©ҳнҠёмқҳ мЎ°н•©мқё 압축л Ҙ 50 MPa, нңЁлӘЁл©ҳнҠё 10 kNВ·m/mм—җм„ңл§Ң 300вҲј350 MPa м •лҸ„мқҳ мқ‘л Ҙк°’мқ„ мӮ°м¶ңн•ҳмҳҖкі , к·ёліҙлӢӨ нҒ° 압축л Ҙкіј нңЁлӘЁл©ҳнҠёмқҳ мЎ°н•©м—җм„ңлҠ” 350вҲј400 MPa м •лҸ„мқҳ мқ‘л Ҙк°’мқ„ ліҙмҳҖлӢӨ. мқҙлҠ” лӘЁл‘җ нҸ° лҜём ңмҠӨмқҳ н•ӯліөкё°мӨҖмқ„ мҙҲкіјн•ҳм—¬ ліҖнҳ•лҘ кІҪнҷ” нҳ„мғҒм—җ мқҳн•ҙ н•ӯліөкё°мӨҖмқҙ нҷ•мһҘлҗҳлҠ” кіјм •м—җ мһҲлҠ” кІғмңјлЎңм„ң 축방н–Ҙ мқ‘л ҘліҙлӢӨлҠ” л§Өмҡ° нҒ° мҲҳмӨҖмқҙлӢӨ. н•ҳм§Җл§Ң мқҙ кІҖнҶ м—җм„ң к°ҖмһҘ мһ‘мқҖ 압축л Ҙкіј нңЁлӘЁл©ҳнҠёмқҳ нҒ¬кё°мЎ°м°ЁлҸ„ мӢӨм ңлЎң л°ңмғқн• мҲҳ мһҲлҠ” нҒ¬кё° мӨ‘м—җм„ңлҠ” нҒ° нҺём—җ мҶҚн•Ёмқ„ мЈјмқҳн•ҙм•ј н•ңлӢӨ. м •л°°м—ҙ л°Ҹ л¶Җл°°м—ҙм—җ л”°лҘё мқ‘л Ҙ м°ЁмқҙлӮҳ ліјнҠё к°ңмҲҳм—җ л”°лҘё мқ‘л Ҙ к°җмҶҢ кІҪн–ҘмқҖ кІҪн–Ҙмқҙ нҳјмһ¬лҗҳм–ҙ лҡңл ·н•ҳм§Җ м•Ҡм•ҳлӢӨ.
м—¬кё°м—җм„ңлҠ” Table 1кіј к°ҷмқҙ көӯлӮҙ н‘ңмӨҖнҳ• нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җм„ң к°ҖмһҘ л№ҲлІҲнһҲ мӮ¬мҡ©лҗҳкі мһҲлҠ” 2ліјнҠё м •л°°м—ҙ мӢңмҠӨн…ңмқ„ лҢҖмғҒмңјлЎң 압축л Ҙ л°Ҹ нңЁлӘЁл©ҳнҠёк°Җ к°ҖмһҘ нҒ° кІҪмҡ°м—җ лҢҖн•ҳм—¬ ліјнҠё мқҙмқҢл¶Җ м—°лӢЁкұ°лҰ¬ л°Ҹ ліјнҠё к°„кІ©мқ„ ліҖнҷ”мӢңмјң к°Җл©° к·ё мҳҒн–Ҙмқ„ 분м„қн•ҙ ліҙм•ҳлӢӨ. мқ‘л ҘмқҖ мғҒкё°мқҳ 분м„қкіј к°ҷмқҙ 축방н–Ҙ мқёмһҘмқ‘л Ҙ л°Ҹ нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙмқ„ кІҖнҶ н•ҳмҳҖлӢӨ.
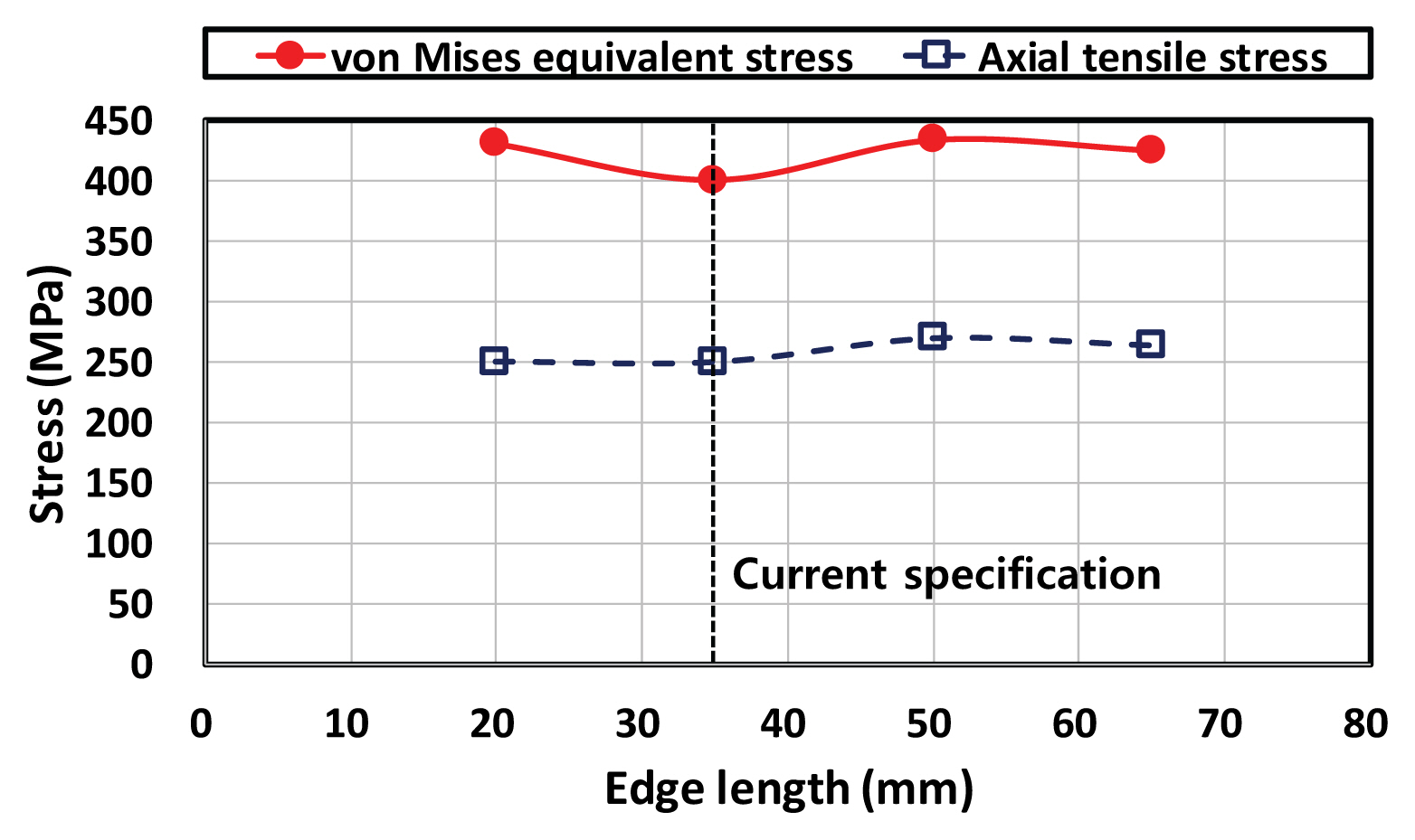
лЁјм Җ нҳ„н–ү н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ё(KEC, 2001)м—җ к·ңм •лҗң м—°лӢЁкұ°лҰ¬мқё 35 mmмқҳ м Ғм Ҳм„ұмқ„ нҢҗлӢЁн•ҳкё° мң„н•ҙ нҳ„н–ү ліјнҠё к°„кІ©мқё 50 mmлҘј мң м§Җн•ң мғҒнғңм—җм„ң м—°лӢЁкұ°лҰ¬ g1мқ„ ліҖкІҪн•ҙ ліҙм•ҳлӢӨ. к·ё кІ°кіј Fig. 15мҷҖ к°ҷмқҙ м—°лӢЁкұ°лҰ¬мҷҖ мқ‘л Ҙ к°„м—җ лҡңл ·н•ң мғҒкҙҖ кҙҖкі„лҘј м°ҫмқ„ мҲҳ м—Ҷм—ҲлӢӨ. мҰү, мқҙ м—°кө¬м—җм„ң кІҖнҶ н•ң 20вҲј65 mm мҲҳмӨҖмқҳ м—°лӢЁкұ°лҰ¬м—җм„ңлҠ” ліјнҠё кө¬л©Қ мЈјліҖмқҳ мқ‘л Ҙмқҙ нҒ¬кІҢ ліҖлҸҷн•ҳм§Җ м•Ҡм•ҳлӢӨ. лҳҗн•ң нҳ„н–ү к·ңм •мқё 35 mmм—җм„ң 축방н–Ҙ мқёмһҘмқ‘л ҘмқҖ мөңмҶҢм—җ к°Җк№Ңмӣ кі , нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘмқҖ мөңмҶҹк°’мқҙм—ҲмңјлҜҖлЎң нҳ„н–ү к·ңм •ліҙлӢӨ м—°лӢЁкұ°лҰ¬лҘј лҠҳл Өм•ј н• н•„мҡ”м„ұмқ„ м°ҫм§ҖлҠ” лӘ»н•ҳмҳҖлӢӨ.
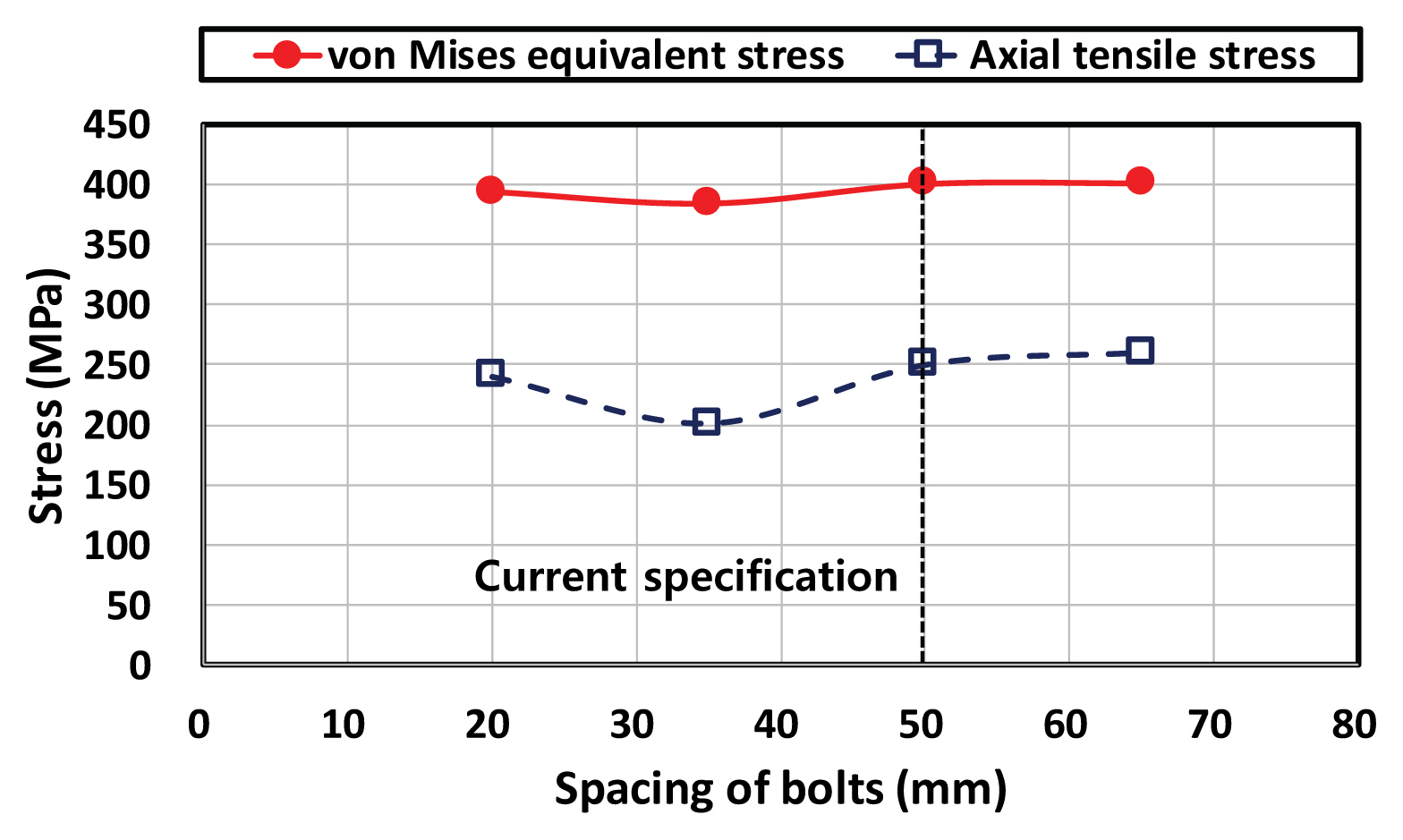
н•ңнҺё нҳ„н–ү н•ңкөӯлҸ„лЎңкіөмӮ¬ м§Җм№Ёмқҳ ліјнҠё к°„кІ©мқё 50 mmмқҳ нғҖлӢ№м„ұмқ„ нҢҗлӢЁн•ҳкё° мң„н•ҙ нҳ„н–ү м—°лӢЁкұ°лҰ¬мқё 35 mmлҘј мң м§Җн•ң мғҒнғңм—җм„ң ліјнҠё к°„кІ© g2лҘј ліҖкІҪн•ҙ ліҙм•ҳлӢӨ. к·ё кІ°кіј Fig. 16кіј к°ҷмқҙ нҳ„н–ү ліјнҠё к°„кІ©мқё 50 mmліҙлӢӨ к°„кІ©мқҙ мўҖ лҚ” мўҒмқҖ 35 mmмқё кІҪмҡ°м—җ к°•нҢҗ ліјнҠё кө¬л©Қ мЈјліҖ мқ‘л Ҙмқҙ мөңмҶҢмҳҖмңјлӮҳ, к·ёліҙлӢӨ лҚ” мўҒмқҖ 20 mm к°„кІ©м—җм„ңлҠ” ліјнҠё кө¬л©Қ мЈјмң„мқҳ нҒ° көӯл¶Җ мқ‘л Ҙмқҙ м„ңлЎң к°„м„ӯлҗҳл©ҙм„ң мқ‘л Ҙмқҙ лӢӨмӢң мҰқк°Җн•ҳлҠ” кІҪн–Ҙмқ„ ліҙмҳҖлӢӨ. н•ңнҺё ліјнҠё к°„кІ©мқҙ 50 mm мқҙмғҒмқё кІҪмҡ° мқ‘л Ҙм—җ нҒ° ліҖлҸҷмқҙ м—Ҷм—ҲлӢӨ. н•ҳм§Җл§Ң ліјнҠё мӨ‘мӢ¬ к°„кІ©мқҙ л„Ҳл¬ҙ мўҒкІҢ лҗҳл©ҙ нҶ нҒ¬ л Ңм№ҳ(torque wrench)лЎң ліјнҠёлҘј мЎ°мқҙлҠ” мһ‘м—…мқҙ м–ҙл өкі , ліјнҠё к°„кІ©мқҙ л„Ҳл¬ҙ л„“кІҢ лҗҳл©ҙ нҢҢнҳ•к°•нҢҗ мқҙмқҢл¶Җ мӮ¬мқҙм—җ л’Өмұ„мӣҖнқҷмңјлЎңл¶Җн„° м§Җн•ҳмҲҳк°Җ м№ЁнҲ¬н•ҳм—¬ к°•нҢҗм—җ л¶ҖмӢқмқҙ л°ңмғқн• мҡ°л Ө л“ұмқҙ мһҲмқ„ кІғмңјлЎң мҳҲмғҒлҗңлӢӨ. л”°лқјм„ң мқҙлҹ¬н•ң мёЎл©ҙм—җм„ңлҸ„ нҳ„н–ү ліјнҠё к°„кІ© кё°мӨҖмқ„ мң м§Җн•ҳлҠ” кІғмқҙ м Ғм Ҳн•ҳлӢӨкі нҢҗлӢЁлҗңлӢӨ.
мқҙмғҒмқҳ 분м„қмңјлЎңл¶Җн„° нҢҗлӢЁн• л•Ң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҳ ліјнҠё мқҙмқҢл¶Җм—җм„ң л°ңмғқн•ҳлҠ” мЈјмҡ” мҶҗмғҒмқё Fig. 2мҷҖ к°ҷмқҖ ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗмқҳ к· м—ҙмқҖ мқҙлҜё ліјнҠё мІҙкІ° лӢЁкі„м—җм„ң ліјнҠё лЁёлҰ¬ лҳҗлҠ” л„ҲнҠёмҷҖ кіЎл©ҙ нҳ•мғҒмқҳ к°•нҢҗмқҙ м ‘мҙүн•ҳлҠ” л¶Җмң„м—җм„ң л°ңмғқн•ң нҒ° көӯл¶Җ мқ‘л Ҙ л°Ҹ мҶҗмғҒ л•Ңл¬ёмңјлЎң мғқк°ҒлҗңлӢӨ. 4.1м Ҳмқҳ 분м„қм—җ мқҳн•ҳл©ҙ мқҙлҹ¬н•ң көӯл¶Җ мқ‘л ҘмқҖ мқҙлҜё н•ӯліөк°•лҸ„ к°Җк№Ңмқҙ л°ңмғқн•ҳкі мһҲлӢӨ. мқҙмІҳлҹј нҢҢнҳ•к°•нҢҗ мӢңкіө лӢЁкі„м—җм„ң л°ңмғқн•ң көӯл¶Җ мқ‘л Ҙм—җ л¶Җк°Җн•ҳм—¬ м„Өкі„ мӢңмқҳ кё°ліё к°Җм •мқё 압축л Ҙ мҷём—җлҸ„ л¶Ҳк°Җн”јн•ң нңЁлӘЁл©ҳнҠёк°Җ л°ңмғқн•Ём—җ л”°лқј нҠ№нһҲ нңЁ кұ°лҸҷм—җ м·Ём•Ҫн•ң л¶Җл°°м—ҙ ліјнҠё кө¬л©Қ мЈјліҖм—җм„ң к·ёлҹ¬н•ң көӯл¶Җ мқ‘л Ҙмқҙ лҚ”мҡұ нҒ¬кІҢ мҰқк°Җн•ҳм—¬ к· м—ҙмқҙ л°ңмғқн•ң кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ. мӢӨм ң ліјнҠёлЎң мІҙкІ°лҗң нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬ј мғҳн”Ңмқ„ н•ҙмІҙн•ҙліҙл©ҙ Fig. 17кіј к°ҷмқҙ к°•нҢҗмқҳ кіЎл©ҙнҳ•мғҒ л•Ңл¬ём—җ ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗ м „мІҙк°Җ ліјнҠё лЁёлҰ¬лӮҳ л„ҲнҠёмҷҖ м ‘н•ҳлҠ” кІғмқҙ м•„лӢҲлқј л‘җ кө°лҚ°л§Ң м ‘н•ҳкІҢ лҗҳл©°, мқҙлҠ” ліјнҠё мІҙкІ° мӢң нҶ нҒ¬м—җ мқҳн•ҙ мғқм„ұлҗң к°•нҢҗ л‘җк»ҳ л°©н–Ҙмқҳ 압축л Ҙмқҙ к·ёлҹ¬н•ң л‘җ мң„м№ҳм—җ 집мӨ‘м Ғмқё көӯл¶Җ мқ‘л Ҙмқ„ мғқм„ұн•Ёмқ„ мқҳлҜён•ңлӢӨ. н•ҳм§Җл§Ң мқҙлҠ” нҢҢнҳ•к°•нҢҗмқҳ нҢҢнҳ•мқҙ нҒ° кіЎлҘ мқ„ к°Җ진 мқҙмғҒ л¶Ҳк°Җн”јн•ң мғҒнҷ©мқҙлӢӨ. мғҒкё°мқҳ 분м„қкіј к°ҷмқҙ ліјнҠё к°ңмҲҳлҘј лҠҳлҰ¬кұ°лӮҳ м—°лӢЁкұ°лҰ¬ лҳҗлҠ” ліјнҠё к°„кІ©мқ„ мЎ°м Ҳн•ҳлҠ” кІғмқҖ ліјнҠё мІҙкІ° мӢң л°ңмғқн•ҳлҠ” көӯл¶Җ мқ‘л ҘкіјлҠ” нҒ° кҙҖл Ём„ұмқҙ м—ҶмңјлҜҖлЎң мөңмў… л°ңмғқн•ҳлҠ” мқ‘л Ҙмқ„ м Җк°җмӢңнӮӨлҠ” лҚ° нҡЁкіјк°Җ нҒ¬м§Җ м•ҠмқҖ кІғмңјлЎң нҢҢм•…лҗҳм—ҲлӢӨ.
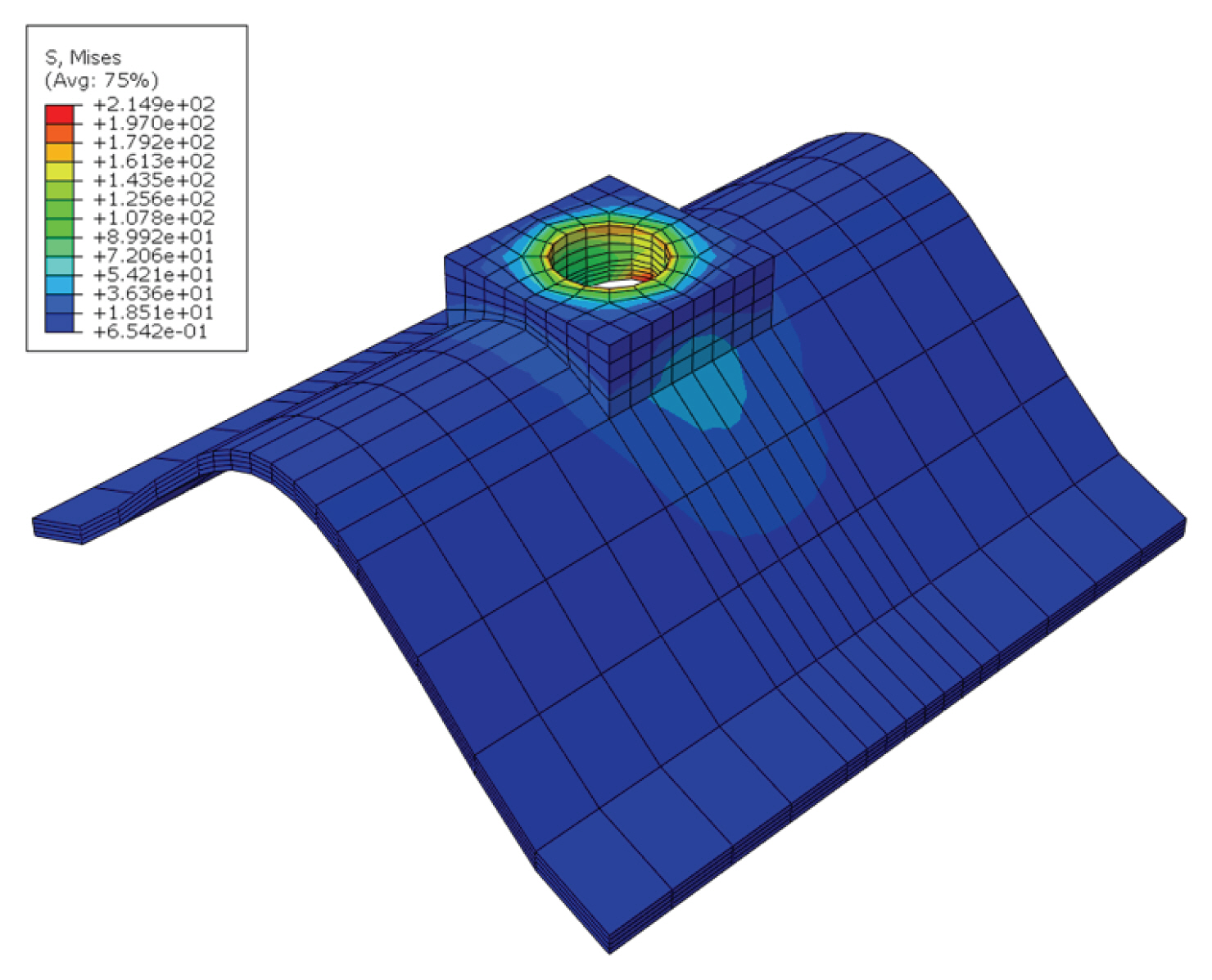
мқҙлҹ¬н•ң көӯл¶Җ мқ‘л Ҙмқ„ мҷ„нҷ”н•ҳкё° мң„н•ҳм—¬ нҶөмғҒм ҒмңјлЎң мӮ¬мҡ©н•ҳлҠ” кІғмқҙ ліјнҠё лЁёлҰ¬ лҳҗлҠ” л„ҲнҠёмҷҖ к°•нҢҗ мӮ¬мқҙм—җ лҒјмӣҢ л„ЈлҠ” мҷҖм…”(washer)мқҙлӢӨ. мқјл°ҳм Ғмқё нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јм—җм„ңлҠ” мҷҖм…”лҘј мӮ¬мҡ©н•ҳм§Җ м•ҠлҠ” кІғмқҙ ліҙнҶөмқҙлӢӨ. н•ҳм§Җл§Ң мҷҖм…” мң л¬ҙлҘј ліҖмҲҳлЎң нҢҢнҳ•к°•нҢҗ мӢӨн—ҳмқ„ мӢӨмӢңн•ң Lee et al. (2007)мқҳ м—°кө¬м—җ мқҳн•ҳл©ҙ к°•нҢҗ л‘җк»ҳм—җ л”°лқј м°Ёмқҙк°Җ мһҲкё°лҠ” н•ҳм§Җл§Ң мҷҖм…”лҘј мӮ¬мҡ©н•ҙлҸ„ к·№н•ңн•ҳмӨ‘мқҖ кұ°мқҳ мң мӮ¬н•ҳл“ к°Җ м•Ҫк°„мқҳ мҰқк°Җм—җ к·ём№ң л°” мһҲлӢӨ. н•ҳм§Җл§Ң мқҙлҠ” нҸүл©ҙ к°•нҢҗм—җ мӮ¬мҡ©н•ҳлҠ” нҸүл©ҙ нҳ•мғҒмқҳ мҷҖм…”лҘј мӮ¬мҡ©н–Ҳкё° л•Ңл¬ёмңјлЎң нҢҗлӢЁлҗңлӢӨ. нҸүл©ҙ мҷҖм…”мқҳ кІҪмҡ° мқҙлҘј м Ғмҡ©н•ҙлҸ„ мғҒкё°м—җм„ң м–ёкёүн•ң к°•нҢҗ кіЎл©ҙкіјмқҳ көӯл¶Җм Ғмқё м ‘мҙүмқ„ н”јн• мҲҳлҠ” м—Ҷкё° л•Ңл¬ёмқҙлӢӨ. л”°лқјм„ң нҢҢнҳ•к°•нҢҗ ліјнҠё мЈјліҖмқҳ көӯл¶Җ мқ‘л Ҙмқ„ мҷ„нҷ”н•ҳкё° мң„н•ҙм„ңлҠ” мқјл°ҳм Ғмқё мҷҖм…”ліҙлӢӨлҠ” к°•нҢҗ кіЎл©ҙкіј л°Җм°©лҗҳлҠ” нҠ№мҲҳн•ң нҳ•нғңмқҳ мҷҖм…”лҘј мӮ¬мҡ©н•ҳлҠ” кІғмқҙ л°”лһҢм§Ғн• кІғмңјлЎң мғқк°Ғлҗҳл©°, кё°мЎҙм—җ кҙҖл Ё нҠ№н—Ҳ(Fixon Inc., 2011)к°Җ м¶ңмӣҗлҗң л°”лҸ„ мһҲлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” 추к°Җм ҒмңјлЎң мқҙлҹ¬н•ң кіЎл©ҙ нҳ•мғҒ мҷҖм…”мқҳ мҳҒн–Ҙмқ„ н•ҙм„қм ҒмңјлЎң кІҖнҶ н•ҙ ліҙм•ҳмңјл©°, к·ё кІ°кіј ліјнҠё мІҙкІ° мӢң мҷҖм…”к°Җ м—Ҷмқ„ л•ҢлҠ” к°•нҢҗмқҳ нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л Ҙмқҙ 235.1 MPaк№Ңм§Җ л°ңмғқн–ҲлҚҳлҚ° л°ҳн•ҙ Fig. 18кіј к°ҷмқҙ кіЎл©ҙ мҷҖм…”лҘј к°•нҢҗ м–‘мӘҪл©ҙм—җ мӮ¬мҡ©н• кІҪмҡ° к·ё к°’мқҙ 214.9 MPaлЎң м•Ҫ 8.6% к°җмҶҢлҗҳлҠ” нҡЁкіјлҘј лӮҳнғҖлӮҙм—ҲлӢӨ. мҷҖм…”мқҳ л‘җк»ҳлӮҳ к°•м„ұ л“ұмқ„ 추к°Җм ҒмңјлЎң мЎ°м Ҳн•ҳл©ҙ нҢҢнҳ•к°•нҢҗмқҳ көӯл¶Җ мқ‘л Ҙмқ„ 추к°ҖлЎң к°җмҶҢмӢңнӮ¬ мҲҳ мһҲмқ„ кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ.
мқҙмҷём—җлҸ„ мқҙлҹ¬н•ң көӯл¶Җ мқ‘л Ҙ к°җмҶҢлҘј мң„н•ң лӘҮк°Җм§Җ лҢҖм•Ҳл“Өмқҙ мһҲмқ„ мҲҳ мһҲлҠ”лҚ°, к·ё мӨ‘ н•ңк°Җм§ҖлҠ” лҸ„лЎңмҡ© мІ м ң к°Җл“ңл Ҳмқјмқҳ мҳҲмҷҖ к°ҷмқҙ нҢҢнҳ•к°•нҢҗ л¶Җмң„ мӨ‘м—җм„ң кіЎл©ҙ нҳ•мғҒмқҙ м•„лӢҢ нҸүл©ҙ нҳ•мғҒмқё мң„м№ҳм—җ ліјнҠёлҘј м„Өм№ҳн•ҳлҠ” кІғмқҙлӢӨ. нҢҢнҳ•к°•нҢҗмқҳ мӮ°кіј кіЁ л¶Җ분мқҙ м•„лӢҢ кІҪмӮ¬л©ҙмқҙ мқҙм—җ н•ҙлӢ№н•ңлӢӨ. н•ҳм§Җл§Ң, нҠ№нһҲ нңЁ кұ°лҸҷ мӢң кІҪмӮ¬л©ҙліҙлӢӨлҠ” мӮ°кіј кіЁм—җм„ң нҒ° мқ‘л Ҙмқҙ л°ңмғқн•ҳкІҢ лҗҳлҜҖлЎң мӮ°кіј кіЁм—җ ліјнҠё мқҙмқҢмқҙ м—Ҷмқ„ кІҪмҡ° мҷёл¶Җн•ҳмӨ‘м—җ лҢҖн•ҳм—¬ к°•нҢҗмқҳ мқјмІҙм„ұмқҙ м Җн•ҳлҗ мҡ°л Өк°Җ мһҲлӢӨ. лҳҗн•ң, нҢҢнҳ•к°•нҢҗмқ„ кіЎл©ҙмқҙ м•„лӢҢ нҸүл©ҙл“Өмқ„ мЎ°н•©н•ҳм—¬ м ҲкіЎлҗң нҳ•нғңлЎң м ңмһ‘н•ҳл©ҙ к·ёлҹ¬н•ң нҸүл©ҙм—җ м„Өм№ҳлҗң ліјнҠё мЈјліҖмқҳ көӯл¶Җ мқ‘л Ҙмқҙ к°җмҶҢлҗ мҲҳ мһҲкІ м§Җл§Ң, кіЎл©ҙкіј 비көҗн• л•Ң м ҲкіЎ нҳ•нғңлҠ” н•ҳмӨ‘ мһ‘мҡ© мӢң кәҪмқё л¶Җмң„м—җ мқ‘л Ҙмқҙ 집мӨ‘лҗҳм–ҙ мўҖ лҚ” нҒ¬кІҢ л°ңмғқн•ҳлҜҖлЎң м·Ём•Ҫл¶Җк°Җ лҗ мҡ°л Өк°Җ мһҲлӢӨ.
нҢҢнҳ•к°•нҢҗ кө¬мЎ°л¬јмқҳ ліјнҠё мқҙмқҢл¶ҖлҠ” м„Өкі„кё°мӨҖмғҒмқҳ к·ңм • л°Ҹ м•Ҳм „лҸ„ кІҖнҶ м Ҳм°Ём—җ л”°лқј м„Өкі„н•ҳкі мһҲм§Җл§Ң, к·ёлҹјм—җлҸ„ л¶Ҳкө¬н•ҳкі мқҙмқҢл¶Җм—җм„ң к°•нҢҗмқҳ к· м—ҙ л“ұ мҶҗмғҒ мӮ¬лЎҖк°Җ ліҙкі лҗҳкі мһҲлӢӨ. мқҙ м—°кө¬м—җм„ңлҠ” кё°мЎҙ н•ҙм„қ лӘЁлҚёмқҳ лӢЁм җл“Өмқ„ нҢҢм•…н•ҳкі к°ңм„ н•ҳм—¬ ліјнҠё мқҙмқҢл¶Җмқҳ мғҒм„ён•ң мң н•ңмҡ”мҶҢ лӘЁлҚёмқ„ кө¬м„ұн•ЁмңјлЎңмҚЁ лӢӨм–‘н•ң ліҖмҲҳм—җ лҢҖн•ң н•ҙм„қм Ғмқё 분м„қмқ„ мӢӨмӢңн•ҳмҳҖмңјл©°, лҸ„м¶ңлҗң мЈјмҡ” кІ°лЎ мқҖ лӢӨмқҢкіј к°ҷлӢӨ.
(1) ліјнҠё мІҙкІ° мӢң к°Ғ ліјнҠё кө¬л©Қ мЈјмң„мқҳ к°•нҢҗм—җм„ң көӯл¶Җ мқ‘л Ҙмқҙ нҒ¬кІҢ л°ңмғқн•ҳмҳҖмңјл©°, нҸ° лҜём ңмҠӨ л“ұк°Җмқ‘л ҘмқҖ н•ӯліөкё°мӨҖм—җ к°Җк№Ңмӣ лӢӨ. мқҙлҠ” кіЎл©ҙ нҳ•мғҒмқҳ нҢҢнҳ•к°•нҢҗмқ„ ліјнҠёлЎң мІҙкІ°н•ҳлҠ” кіјм •м—җм„ң л°ңмғқн•ҳлҠ” ліјнҠёмҷҖ к°•нҢҗмқҳ көӯл¶Җм Ғмқё м ‘мҙүм—җ мқҳн•ң мқ‘л Ҙ 집мӨ‘ л•Ңл¬ёмңјлЎң нҢҗлӢЁлҗңлӢӨ. м—¬кё°м—җ 압축л Ҙ л°Ҹ нңЁлӘЁл©ҳнҠёк°Җ 추к°ҖлЎң мһ‘мҡ©н•Ём—җ л”°лқј к·ёлҹ¬н•ң мқ‘л Ҙмқҙ н•ӯліөк°•лҸ„ мқҙмғҒ лҚ”мҡұ мҰқк°Җн•ҳлҠ” нҳ„мғҒмқ„ ліҙмҳҖлӢӨ. л”°лқјм„ң ліјнҠё кө¬л©Қ мЈјліҖ к°•нҢҗмқҳ к· м—ҙмқҖ мқҙмІҳлҹј ліјнҠё мІҙкІ° мӢң л°ңмғқн•ҳлҠ” нҒ° көӯл¶Җ мқ‘л Ҙм—җ кё°мқён•ң л°”к°Җ нҒ¬лӢӨкі нҢҗлӢЁлҗңлӢӨ.
(2) м„Өкі„м§Җм№ЁмғҒ мқҙмқҢл¶Җ к°•лҸ„ мқҙн•ҳмқҳ 압축л Ҙл§Ң мһ‘мҡ© мӢңм—җлҸ„ ліјнҠё кө¬л©Қ мЈјліҖм—җ көӯл¶Җм ҒмңјлЎң н•ӯліөк°•лҸ„м—җ лҸ„лӢ¬н•ҳлҠ” л¶Җ분мқҙ лӮҳнғҖлӮ¬лӢӨ. л”°лқјм„ң, м„Өкі„ к°Җм •лҢҖлЎң 압축л Ҙл§Ң мһ‘мҡ©н•ҳлҚ”лқјлҸ„ нҳ„мһ¬ к·ңм •мғҒмңјлЎңлҠ” ліјнҠё мқҙмқҢл¶Җ к· м—ҙмқ„ мҷ„м „нһҲ л°©м§Җн•ҳкё° м–ҙл Өмҡҙ кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ.
(3) нңЁлӘЁл©ҳнҠёк°Җ лӢЁлҸ… лҳҗлҠ” мӢӨм ң нҳ„мғҒкіј к°ҷмқҙ 압축л Ҙкіј лҸҷмӢңм—җ мһ‘мҡ©н• л•Ң 축방н–Ҙ мқ‘л Ҙмқҳ кІҪмҡ° л¶Җл°°м—ҙм—җм„ңмқҳ мқ‘л Ҙмқҙ м •л°°м—ҙм—җм„ңмқҳ мқ‘л ҘліҙлӢӨ нҒ¬кІҢ л°ңмғқн•ҳмҳҖлӢӨ. мқҙлҠ” кё°мЎҙм—җ м •л°°м—ҙліҙлӢӨлҠ” л¶Җл°°м—ҙ ліјнҠём—җм„ң мҶҗмғҒмқҙ лҚ” л§Һмқҙ кҙҖм°°лҗң мӮ¬мӢӨкіј л¶Җн•©н•ңлӢӨ. 압축л Ҙкіј нңЁлӘЁл©ҳнҠёмқҳ лҸҷмӢң мһ‘мҡ© мӢң л¶Җл°°м—ҙм—җм„ңлҠ” лҢҖл¶Җ분 н•ӯліөк°•лҸ„лҘј мҙҲкіјн•ҳлҠ” мқ‘л Ҙмқҙ л°ңмғқн•ҳмҳҖлӢӨ. ліјнҠё кө¬л©Қ мЈјліҖмқҳ көӯл¶Җ мқ‘л ҘмқҙлҜҖлЎң ліјнҠё к°ңмҲҳм—җ л”°лҘё 축방н–Ҙ мқ‘л Ҙ нҒ¬кё°мқҳ кІҪн–ҘмқҖ лӘ…нҷ•м№ҳ м•Ҡм•ҳлӢӨ. мқҙлҠ” 2ліјнҠё лҝҗ м•„лӢҲлқј 3ліјнҠё л°Ҹ 4ліјнҠёлҸ„ л¶Җл°°м—ҙлЎң л°°м№ҳлҗҳл©ҙ мҶҗмғҒм—җ м·Ём•Ҫн• мҲҳ мһҲмқҢмқ„ мқҳлҜён•ҳл©°, мӢӨм ң мӮ¬лЎҖмҷҖлҸ„ л¶Җн•©н•ңлӢӨ.
(4) м—°лӢЁкұ°лҰ¬мқҳ кІҪмҡ° нҳ„н–ү 35 mmлҘј нҸ¬н•Ён•ҳм—¬ 20вҲј65 mm мҲҳмӨҖмқҳ м—°лӢЁкұ°лҰ¬м—җм„ңлҠ” ліјнҠё кө¬л©Қ мЈјліҖмқҳ мқ‘л Ҙмқҙ нҒ¬кІҢ ліҖлҸҷлҗҳм§Җ м•Ҡм•ҳмңјлҜҖлЎң нҳ„н–ү к·ңм •мқҖ м Ғм Ҳн•ң мҲҳмӨҖмңјлЎң нҢҢм•…лҗңлӢӨ. н•ңнҺё ліјнҠё к°„кІ©мқҖ нҳ„н–ү 50 mmлҘј нҸ¬н•Ён•ҳм—¬ 20вҲј65 mm лІ”мң„лҘј кІҖнҶ н•ҳмҳҖмңјл©°, м „л°ҳм ҒмңјлЎң мң мқҳлҜён• м •лҸ„лЎң мқ‘л Ҙмқҙ нҒ¬кІҢ ліҖлҸҷн•ҳм§ҖлҠ” м•Ҡм•ҳмңјлҜҖлЎң мӢңкіөм„ұмқҙлӮҳ лӮҙкө¬м„ұмқ„ кі л Өн• л•Ң нҳ„н–ү ліјнҠё к°„кІ©мқҖ м Ғм Ҳн•ҳлӢӨкі нҢҗлӢЁлҗңлӢӨ.
(5) ліјнҠё мІҙкІ° лӢЁкі„м—җм„ң л°ңмғқн•ҳлҠ” нҒ° көӯл¶Җ мқ‘л Ҙмқ„ м Җк°җмӢңнӮӨлҠ” кІғмқҙ ліјнҠё мқҙмқҢл¶Җ мҶҗмғҒмқ„ мӨ„мқҙлҠ”лҚ° нҡЁкіјм Ғмқё кІғмңјлЎң нҢҢм•…лҗҳлҜҖлЎң, лӘҮк°Җм§Җ лҢҖм•Ҳмқ„ м ңмӢңн•ҙ ліҙм•ҳлӢӨ. н•ң мҳҲлЎң к°•нҢҗ кіЎл©ҙм—җ л°Җм°©лҗҳлҠ” нҠ№мҲҳн•ң нҳ•нғңмқҳ мҷҖм…”лҘј мӮ¬мҡ©н• кІҪмҡ° н•ҙм„қмқ„ нҶөн•ҙ ліјнҠё мІҙкІ° мӢңмқҳ көӯл¶Җ мқ‘л Ҙмқҙ к°җмҶҢн•ҳлҠ” кІғмқ„ нҷ•мқён• мҲҳ мһҲм—ҲлӢӨ. н•ңнҺё мғҒкё°мқҳ 분м„қкіј к°ҷмқҙ ліјнҠё к°ңмҲҳлҘј лҠҳлҰ¬кұ°лӮҳ м—°лӢЁкұ°лҰ¬ лҳҗлҠ” ліјнҠё к°„кІ©мқ„ мЎ°м Ҳн•ҳлҠ” кІғмқҖ ліјнҠё мІҙкІ° мӢң л°ңмғқн•ҳлҠ” көӯл¶Җ мқ‘л ҘкіјлҠ” нҒ° кҙҖл Ём„ұмқҙ м—ҶмңјлҜҖлЎң мөңмў… л°ңмғқн•ҳлҠ” мқ‘л Ҙмқ„ м Җк°җмӢңнӮӨлҠ” лҚ° нҡЁкіјк°Җ нҒ¬м§Җ м•ҠмқҖ кІғмңјлЎң нҢҢм•…лҗҳм—ҲлӢӨ.
к°җмӮ¬мқҳ кёҖ
ліё м—°кө¬лҠ” 2017л…„ н•ңкөӯлҸ„лЎңкіөмӮ¬ м—°кө¬мӮ¬м—… вҖңм•”кұ°кө¬мЎ°л¬јмқҳ м•Ҳм „м„ұнҸүк°Җ л°Ҹ ліҙк°•л°©лІ• м—°кө¬вҖқмқҳ кіөлҸҷм—°кө¬л№„лЎң мҲҳн–үлҗҳм—ҲмҠөлӢҲлӢӨ. м—°кө¬м§Җмӣҗм—җ к°җмӮ¬л“ңлҰҪлӢҲлӢӨ.
TableВ 1
Variables in Analyses of Bolted Connection
| # | Number of bolts | Joint lap | Axial compressive stressa) (MPa) | Bending momentb) (kNВ·m/m) | Edge length (mm) | Spacing of bolts (mm) |
|---|---|---|---|---|---|---|
| 1 | 2 | Correct | 50 | 10 | 35 | 50 |
| 2 | Incorrect | |||||
| 3 | Correct | 15 | ||||
| 4 | Incorrect | |||||
| 5 | Correct | 100 | 10 | |||
| 6 | Incorrect | |||||
| 7 | Correct | 15 | ||||
| 8 | Incorrect | |||||
| 9 | 3 | Correct | 50 | 10 | ||
| 10 | Incorrect | |||||
| 11 | Correct | 15 | ||||
| 12 | Incorrect | |||||
| 13 | Correct | 100 | 10 | |||
| 14 | Incorrect | |||||
| 15 | Correct | 15 | ||||
| 16 | Incorrect | |||||
| 17 | 4 | Correct | 50 | 10 | ||
| 18 | Incorrect | |||||
| 19 | Correct | 15 | ||||
| 20 | Incorrect | |||||
| 21 | Correct | 100 | 10 | |||
| 22 | Incorrect | |||||
| 23 | Correct | 15 | ||||
| 24 | Incorrect | |||||
| 25 | 2 | Correct | 100 | 15 | 20 | 50 |
| 26 | 35 | 50 | ||||
| 27 | 50 | 50 | ||||
| 28 | 65 | 50 | ||||
| 29 | 35 | 20 | ||||
| 30 | 35 | 35 | ||||
| 31 | 35 | 65 |
References
AISI (American Iron and Steel Institute) (2002). Handbook of steel drainage & highway construction products. 2nd Canadian ed.

Bakht, B, and Agarwal, AC (1988) On distress in pipe-arches. Canadian Journal of Civil Engineering, Vol. 15, No. 4, pp. 589-595.

Choi, MS (2005). Evaluation of compressive seam strength and flexural strength of corrugated structural plates. MasterвҖҷs thesis. Hanyang University.

Daewoo E&C and Ajou University (2017). Safety assessment, repair and strengthening method of corrugated steel plate structures.

Fixon Inc (2011). A bolt with the attached washer for corrugated steel plates. Design patent. 30-05995740001.

Han, JH, Choi, JK, Heo, IS, and Kim, SB (2008) Slip behavior of high-tension bolted joints subjected to compression force. Journal of Korean Society of Steel Construction, Vol. 20, No. 2, pp. 279-288.

Kang, SP (2004). Evaluation of limitary edge lap and bolt hole spacing for the corrugated plate. MasterвҖҷs thesis. Inha University.

KEC (Korea Expressway Corporation) (2001). Guidelines of design and construction of soil-steel structures. KEC Expressway Research Institute.

Lee, JH (2012). Evaluation of deep corrugated steel plate seam strength using numerical analysis method. MasterвҖҷs thesis. Dankook University.

Lee, JK, Cho, SM, Lee, JG, and Yoon, TY (2007) Analysis of influence factors on the bolt hole tears in soil steel structures. Journal of the Korean Society of Civil Engineers, Vol. 27, No. 2C, pp. 129-137.

Lee, BJ, Yoon, JY, Nam, MS, and Park, YH (2014) Development of performance evaluation method for structures based on 3D geometric information and image processing. Magazine of the Korea Institute for Structural Maintenance and Inspection, Vol. 18, No. 2, pp. 17-25.

Mikhailovsky, L, Kennedy, DJL, and Lee, RWS (1992) Flexural behavior of bolted joints of corrugated steel plates. Canadian Journal of Civil Engineering, Vol. 19, No. 5, pp. 896-905.

- TOOLS
-
METRICS

-
- 0 Crossref
- 4,212 View
- 84 Download
- Related articles in KOSHAM
-
Analytical Study on Thermal Properties of Hollow Slab at Elevated Temperature2015 April;15(2)