왜곡도계수 및 표본크기에 따른 확률 분포형의 극치 수문량 추정에 관한 연구

A Study on the Estimation of the Extreme Quantile of Probability Distribution According to Skewness Coefficient and Sample Size

Article information

J. Korean Soc. Hazard Mitig. 2018;18(7):485-496

Publication date (electronic) : 2018 December 31

doi : https://doi.org/10.9798/KOSHAM.2018.18.7.485

Jinseok Jung ^*, Hyunjun Ahn ^**, Changsam Jung ^***, Jun-Haeng Heo^,^****

^*Member, Engineer, KG Engineering Corporation

^**Ph.D. Candidate, School of Civil and Environmental Engineering, Yonsei University

^***Professor, Department of Civil and Environmental Engineering, Induk University

^****Member, Professor, School of Civil and Environmental Engineering, Yonsei University

정진석^*, 안현준^**, 정창삼^***, 허준행^,^****

^*정회원, KG엔지니어링 종합건축사사무소 공학석사 사원

^**연세대학교 건설환경공학과 석박통합과정

^***인덕대학교 토목환경공학과 공학박사 교수

^****정회원, 연세대학교 건설환경공학과 공학박사 교수

교신저자, 정회원, 연세대학교 건설환경공학과 공학박사 교수(Tel: +82-2-2123-2805, Fax: +82-2-6280-1597, E-mail: jhheo@yonsei.ac.kr)

Received 2018 October 22; Revised 2018 October 24; Accepted 2018 November 12.

Abstract

본 연구에서는 확률 분포에서 오른쪽 꼬리 부분의 극치 수문량 추정 시 안정적인 값을 추정하는 확률분포형을 평가하기 위해 Monte Carlo 모의를 수행하여 그 성능을 비교·분석하였다. 이를 위해 수문자료의 빈도해석에 적합한 것으로 알려진 generalized extreme value (GEV), Gumbel (GUM), generalized logistic (GLO), normal (NOR) 분포 등의 총 4개 확률분포형을 사용하였으며, 매개변수 추정 방법으로는 확률가중모멘트법을 사용하였다. 다양한 왜곡도 범위와 표본 크기를 고려한 임의 표본 생성을 위해 Wakeby 분포를 이용하였다. 왜곡도계수는 우리나라 강우자료에서 관측될 수 있는 0.0에서 4.0사이의 왜곡도계수를 0.5간격으 로 고려하였다. 또한 자료 개수에 따른 성능 평가를 위해 표본크기 20, 30, 50, 70, 100에 대해 분석을 수행하였다. 이와 같은 가정으로 총 45가지의 표본발생 경우에 대하여 4가지 확률분포형을 적용하여 추정한 확률수문량의 결과를 비교·분석하였다. 평가방법으로는 재현기간 10∼1000년의 확률수문량을 도시위치공식을 통해 Gumbel 확률지에 도시화하여 4가지 오차 평가기법을 이용하여 최적 분포형을 선정하였으며, modified Anderson Darling (MAD) 검정 방법을 이용하여 결과를 비교·분석하였다. 모의실험 결과 왜곡도계수와 표본크기 따라 극치 수문량을 가장 잘 추정하는 확률분포형은 다르게 나타났고, 따라서 최적 확률분포형의 결정에 왜곡도계수와 표본크기가 많은 영향을 미치는 것으로 나타났다.

Trans Abstract

In this study, probability distribution selection was assessed for right-tail quantile using Monte Carlo simulation. Four probability distributions, including the generalized extreme value (GEV), Gumbel (GUM), generalized logistic (GLO), and normal (NOR) were used and the probability weighted moments method was used for parameter estimation. The Wakeby distribution was adopted as the random generating model that could consider various skewness values. The skewness coefficients of the Wakeby model were set as 0.0 to +4.0 at intervals of +0.5, which are typical values for South Korea. In addition, the sample size was set to 20, 30, 50, 70, or 100. Using these combinations, a total of 45 cases (9 skewness values and 5 sample sizes) were generated and rainfall quantiles from four probability distributions were analyzed. The rainfall quantiles of the return period from 10 to 1,000 years were calculated and plotted on Gumbel probability paper by plotting position formula. The appropriate probability distribution was selected using four performance criteria and the modified Anderson Darling (MAD) goodness of fit test was used for comparative analysis. The appropriate probability distribution varied with the skewness value and sample size, indicating that the appropriate probability distribution is significantly influenced by the coefficient of skewness and sample size.

Keywords: 극치 분포; Monte Carlo 모의; 오른쪽 꼬리; 왜곡도계수; 확률강우

Keywords: Extreme Distribution; Monte Carlo Simulation; Right-tail; Skewness Cofficients; Rainfall Quantile

1. 서 론

빈도해석은 수문자료의 관측기간이 짧은 경우 추정된 확률강우량의 불확실성이 크므로 지점 내 충분한 표본 크기의 확보가 필수적이다. Benson (1962)은 빈도해석을 통해 자료 크기의 2배보다 작은 재현기간에 대해 신뢰할만한 확률수문추정량을 산정할 수 있다고 주장하였으며, Hosking et al. (1984)은 신뢰성있는 확률 수문량은 비초과확률이 1-1/n (n = 자료기간)보다 작을 경우에만 얻을 수 있다고 주장하였다. 미국의 NOAA Atlas14 (Bonnin et al., 2004)에서는 자료기간이 50년 이상일 경우 지점빈도해석을 적용할 것을 권장하고 있으며, 영국에서 발행한 Flood Estimation Handbook (Institute of Hydrology, 1999)에 의하면 지점빈도해석은 구하려는 재현기간이 작고 대상 자료는 충분히 길 경우 사용할 것을 권장하였다. 따라서 보다 안정적인 확률강우량을 추정하기 위해서는 해당지점의 뚜렷한 통계적 특성을 나타낼 수 있는 긴 관측 자료가 필요하나, 우리나라에서는 비교적 짧은 기간의 강우 관측자료로부터 연 최대치 계열을 구축한 후 강우 빈도해석을 통하여 산정된 확률강우량을 사용하고 있다. 현재 기상청 일부 지점에서는 약 50년 이상의 강우자료를 구축하고 있으나, 이는 선진국과 비교하면 상대적으로 적은 개수의 자료를 이용하여 확률강우량을 산정하고 있는 실정이다. 기상청의 경우 전체 79개 지점에서 평균 40년 정도의 자료가 구축되어 있으며, 이 중 30년 이상의 강우자료가 확보되어 있는 지점은 64개 지점이다. 이처럼 우리나라 수문통계분야에서는 주어진 자료가 한정되어 있는 현실 속에서 표본의 크기나 통계적 특성에 따라 적절한 확률분포형을 찾는 노력을 하는 것이 한계라 할 수 있다.

한편, 전세계적으로 관측된 표본자료를 적절히 표현해줄 수 있는 분포모형에 대한 연구가 활발히 진행되어왔는데, 미국 수자원평의회(U.S. Water Resources Council, 1976)는 홍수 빈도해석 지침서에서 지역화된 왜곡도 계수를 이용한 log-Pearson type Ⅲ 분포를 사용할 것을 추천하였으며, 영국은 Flood Studies Report (NERC, 1975)를 발간하여 general extreme value (GEV) 분포를 홍수 빈도해석시 추천한 바 있으나, 1999년 발간된 Flood Estimation Handbook 지침서에서는 generalized logistic (GLO) 분포를 사용하도록 권장하고 있다. 또한 이탈리아는 two component extreme value (TCEV) 분포의 사용을 추천하고 있으며(Rossi et al., 1984), 중국은 log-Pearson type Ⅲ 분포를 사용하고 있고(Singh, 2012), Haktanir et al. (2013)은 터키의 강우 자료를 기반으로 모의실험을 한 결과 3변수 gamma 분포를 추천하였다. 캐나다의 경우 강우자료를 Gumbel 분포형을 사용하여 모멘트법으로 매개변수를 추정하였고 이를 재현기간별 IDF (Intensity-Duration-Frequency)의 값으로 제시하였으며(Hogg et al., 1989), 스웨덴의 경우 확률가중모멘트법으로 매개변수를 추정한 GEV 분포를 권장하고 있다(Alecandersson et al., 2001). 독일은 재현기간 10∼10,000년까지는 Gumbel 분포를 사용을 추전하고 있으며(Bartels et al., 1997), 뉴질랜드에서는 재현기간 2∼150년까지 확률가중모멘트법으로 매개변수를 추정한 GEV 분포가 가장 적합하다는 연구를 결과를 제시하였다(Thompson, 1992). 이처럼 외국의 경우 다양한 분포형을 사용하고 있지만, 그 중 GEV 분포가 수문빈도해석에서 가장 많이 권장되는 것으로 조사되었다.

우리나라의 경우에는 Heo and Kim (1995)은 우리나라 22개 관측지점의 연 최대 강우자료를 이용하여 지속기간별 확률분포형을 선정하기 위하여 확률가중모멘트법을 이용하여 Gumbel 분포를 우리나라 대표 강수 확률분포형으로 선택한 바 있으며, Lee et al. (2000)도 21개 관측지점의 자료를 이용하여 대표 확률 분포형으로 Gumbel 분포를 선정하였다. 한편, Heo et al. (2007)에 따르면 378개 우량관측지점의 최적분포형을 GLO 분포형으로 선정하여 지역빈도해석을 수행한 바 있으며, Um et al. (2012)은 강원도 지역에서의 최적 확률분포형으로 GLO 분포를 선정한 바 있다.

또한, 확률분포형에 대한 연구 뿐만 아니라 추정된 확률분포형 모형 중 적절한 확률분포형을 가려내고자 하는 연구 역시 활발히 진행되어 왔는데, Shin, Kim, et al. (2010)은 GEV 분포와 GLO 분포에 대해서 표본크기와 매개변수에 따른 modified Anderson-Darling (MAD)의 검정 통계량 값을 제시하였으며, Shin, Sung, et al. (2010)은 극치 분포형 중 하나인 Gumbel 분포에 대하여 MAD 검정 방법을 포함한 다양한 적합도 검정 기법을 적용하여 모의실험을 수행한 결과 MAD 검정 방법이 다른 적합도 검정 방법보다 더 우수한 기각력을 보였다고 주장하였다. 또한 Shin et al. (2012)은 GEV 분포와 GLO 분포에 대해서도 기존 검정방법들 보다 MAD 검정방법의 기각력이 더 우수함을 보였으며, Heo et al. (2013)은 MAD 검정 통계량 값에 대한 회귀 방정식을 제시하고 이를 바탕으로 국내 지점을 대상으로 다른 적합도 검정 기법들과 비교한 결과 다른 검정 방법들보다 MAD 검정 방법의 기각력이 우수한 것을 확인하였다.

본 연구에서는 Monte Carlo 모의실험을 통해 충분한 횟수의 모의자료를 발생시키고 자료가 가지고 있는 왜곡도계수와 표본크기에 따른 확률분포형의 극치 수문량 추정 능력을 비교·평가하고자 한다. 이를 위해 매개변수가 많기 때문에 전체적으로 다른 분포형의 형상을 잘 묘사할 수 있는 Wakeby 분포를 통해 표본 자료를 발생시키고 수문빈도해석에서 많이 사용되는 generalized extreme value (GEV), Gumbel (GUM), generalized logistic (GLO) 분포와 왜곡도가 없는 normal (NOR) 분포에 적용하여 왜곡도 계수(0.0, +1.0, +1.5, +2.0, +2.5, +3.0, +3.5, +4.0)에 따른 확률수문량을 추정하였다. 추정된 확률수문량을 재현기간에 따라 Gumbel 확률지에 도시화하여 평균제곱근오차(root mean square error, RMSE), 편의(bias), 평균상대오차(mean relative difference, MRD), 평균절대상대오차(mean absolute relative difference, MARD) 등 4가지 평가기법을 사용하여 왜곡도계수와 표본크기에 따른 최적 확률분포형을 선정하였다. 또한 이 결과의 비교·검증을 위해 오른쪽 극치값에 가중치를 준 modified Anderson-Darling (MAD) 적합도 검정을 이용하여 왜곡도계수 및 표본크기에 따른 확률분포형을 검증하였다.

2. 기본 이론

2.1 Wakeby 분포

Wakeby 분포의 확률밀도함수는 Eq. (1)과 같이 나타낼수 있으며 Hosking and Wallis (1997)에 따르면 Eq. (2)와 같이 역함수 형태로 정의할 수 있다.

(1) f(x)=1[ab(1-F)b-1+cd(1-F)-d-1]

(2) x=m+a{1-(1-F)b}-c{1-(1-F)-d}

여기서 F는 누가분포함수로서, F=P[X≤x]로 표시된다. Wakeby 분포의 매개변수는 m, a, b, c, d 총 5개로 매개변수가 많아 여러 분포형을 표현하는데 유리하며 b는 분포형의 왼쪽 꼬리부분인 극소치 자료를 제어하고, d는 분포형의 오른쪽 꼬리부분인 극대치 자료를 제어한다(Maeng et al., 2006; Rahman et al., 2015). 이러한 Wakeby 분포를 활용하여 Monte Carlo 모의실험을 하는 연구가 꾸준히 진행되어 오고 있으며(Su et al., 2009; Heo et al., 2013; Oztekin, 2011), 특히 Landwehr et al. (1979a, 1979b)은 Monte Carlo 모의실험을 하는데 있어 여러 가지 형태의 분포형을 잘 형상화 할 수 있는 6가지 Wakeby 분포를 제시한 바 있다.

2.2 확률분포형 및 확률가중모멘트법

본 연구에서는 수문빈도해석에서 많이 사용되는 GEV, GUM, GLO, NOR 분포형을 사용하였으며, 매개변수 추정방법으로는 확률가중모멘트법(probability weighted moment method, PWM)을 사용하였다. 자세한 내용은 Greenwood et al. (1979)을 참고하였다. Table 1에는 각 분포형의 누가분포함수(cumulative distribution function, CDF)와 확률변수의 범위를 정리하였다. 여기서 μ는 위치매개변수(location parameter), α는 규모매개변수(scale parameter), β는 형상매개변수(shape parameter)를 나타낸다.

Table 1

Cumulative Distribution Functions and Ranges of Random Variables

2.3 평가 방법

2.3.1 평균제곱근오차와 편의

본 연구에서는 일반적인 모델의 예측값과 실제 관측값의 차이를 다룰 때 흔히 사용하는 척도인 평균제곱근오차(root mean square error, RMSE)와 편의(bias)를 사용하여 오차에 대한 비교 연구를 수행하였다. RMSE와 bias는 각각 Eqs. (3) and (4)와 같다.

(3) RMSE(θ1,θ)=MSE(θ1,θ)=E((θ1-θ)2)

(4) bias=E(θ^)-θ

여기서 θ₁은 추정값, θ는 관측값, θ^는 편의추정량 (biased estimator)을 나타낸다.

2.3.2 평균상대오차와 평균절대상대오차

또한 본 연구에서는 앞 절의 일반적인 평가 방법과는 달리 평균상대오차(mean relative difference, MRD)와 평균절대상대오차(mean absolute relative difference, MARD)를 활용하여 분석을 수행하였다. MRD와 MARD는 사다리꼴의 면과 면의 오차를 나타내는 2차원적 오차로 Eqs. (5)∼(8)와 같이 나타낼 수 있다.

(5) RDij=AFCij-AFCpdAFCpd

(6) ARDij=|AFCij-AFCpdAFCpd|

(7) MRDj=∑i=1m(RDij)/m

(8) MARDj=∑i=1m(ARDij)/m

여기서 RD_ij는 상대오차(relative difference), ARD_ij는 절대상대오차(absolute relative difference)를 뜻하고 AFC_ij는 i, j년 재현기간 사이의 확률분포 빈도곡선의 사다리꼴 면적, AFC_pd는 모분포의 빈도곡선 사다리꼴 면적을 뜻하며, m은 반복 시행 횟수이다. Fig. 1은 왜곡도계수와 표본크기가 각각 1과 100일 때 모의실험을 이용해 나온 결과값을 Gumbel 확률지에 도시화한 것이다. 음영으로 된 사다리꼴은 RD의 값으로 모분포와 GUM 분포형의 오차를 나타낸다.

Fig. 1

Quantile Curves of the GEV, GUM, GLO, and NOR Distributions for the Wakeby Distribution (C_s = 1.0 and n = 100)

2.4 Modified Anderson-Darling 검정

Ahmad et al. (1988)은 기존의 Anderson-Darling 검정방법에서 가중치 함수를 수정한 modified Anderson-Darling (MAD) 검정 방법을 제안하였다. MAD 검정은 오른쪽 극치 부분에 ψ(x)=[1-F(x)]^-1와 같은 가중치를 부여하여 왼쪽 극치부분보다 더 큰 가중치를 주는 것으로 검정 통계량은 AU²₂으로 나타내고 Eq. (9)과 같이 쓸 수 있다.

(9) AUn2=n∫-∞+∞[Fn(x)-F(x)]1-F(x)dF(x)

여기서 F(x)는 추정된 매개변수를 포함하는 누가분포함수, F_x(n)은 경험적 누가분포함수, n은 자료개수를 나타낸다. Eq. (9)는 계산의 편의를 위해 다음과 같이 Eq. (10)으로 나타낼 수 있다.

(10) AUn2≈n2-2∑j=1nF(x(j))-∑j=1n{2-(2j-1)n}log{1-F(x(j))}

여기서 x₍₁₎ ≤ x₍₂₎ ≤ ⋯ ≤ x_(n)은 순서통계량이며, n은 자료 기간이다.

3. 적용 및 결과

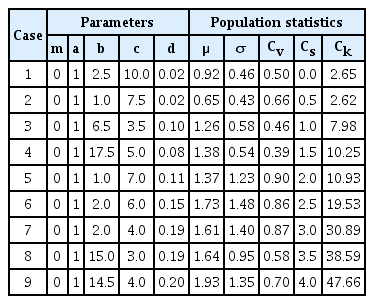
본 연구에서는 극치 분포의 오른쪽 꼬리 부분만을 고려하여 확률수문량만을 추정할 때 보다 안정적인 확률수문량을 산정하는 확률분포형을 알아보기 위해 Monte Carlo 모의를 수행하였다. 우선 모의실험을 수행하기에 앞서 효과적인 실험을 위해 우리나라 30년 이상의 자료를 보유한 기상청 지점의 시 단위 강우자료를 활용하여 지속기간 1, 2, 3, 6, 9, 12, 18, 24, 48, 72시간 자료에 대해 왜곡도계수를 산정하여 Table 2와 같이 정리하였다. Table 2를 살펴보면 음영으로 표시한 청주지점에서 지속기간 1시간 자료의 왜곡도계수가 –0.14로 가장 작은 값을 나타냈으며 보은지점에서는 지속기간 1시간 자료의 왜곡도계수가 4.05로 가장 큰 값을 나타났다. 64개 지점의 지속기간 10개 자료 총 640개 자료세트에 대한 왜곡도계수를 산정해 본 결과, 약 80% 이상의 자료들이 왜곡도계수 범위가 0.5∼1.5에 포함되었으며, 청주, 정읍, 문경, 구미, 남원 등 총 5개 지점에서 음의 왜곡도계수가 나타난 것을 확인 하였다. 따라서 본 연구에서는 우리나라 수문자료로부터 관측될 수 있는 왜곡도계수의 범위인 –0.14부터 +4.05 중에서 왜곡도계수 0.0, +1.0, +1.5, +2.0, +2.5, +3.0, +3.5, +4.0을 모의실험 조건으로 선정하였다. 또한 표본크기에 따른 변화와 불확실성을 고려하기 위하여 표본 크기 또한 20, 30, 50, 70, 100으로 나누어 진행하였다. 일반적으로 극치 분포 모형을 구분 짓는데 가장 영향을 미치는 인자는 형상매개변수(shape parameter)이고, 이러한 형상매개변수는 표본 자료의 왜곡도 계수와 직접적인 연관성이 있다고 알려져 있다. 따라서 본 연구에서는 다른 분포모형들에 비해 상대적으로 많은 매개변수를 가지고 있어 여러가지 분포형들을 표현하는데 있어 유리하고, 다양한 왜곡도를 표현할 수 있는 5변수 Wakeby 분포를 이용하여 왜곡도계수 및 표본크기의 따른 각 경우의 수마다 1000번씩 모의실험을 수행하였다. 이 때 모의실험 조건의 왜곡도를 발생시킬 Wakeby 모형의 매개변수는 Table 3과 같다. 여기서, μ, σ, C_v, C_s, C_k는 각각 평균, 표준편차, 변동계수, 왜곡도계수, 첨예도계수를 나타낸다.

Table 2

Skewness Coefficients of KMA Stations in Korea

Table 3

Parameters of Wake by Distribution According to Skewness Coefficients

적용 분포형은 GEV, GUM, GLO, NOR 분포를 선정하였으며 매개변수 추정방법으로는 PWM을 사용하였다. PWM은 모멘트 방법에 의한 추정보다 편의가 작고 표본크기가 작은 경우 최우도 방법보다 정확도측면에서 안정적이며, 표본 크기나 자료의 이상치가 있는 경우에도 크게 왜곡되지 않는 장점이 있다. 적합도 검정으로는 오른쪽 극치값에 상대적으로 큰 가중치를 주는 modified Anderson-Darling (MAD) 검정 방법을 사용하여 RMSE, bias, MRD, MARD의 결과값과 비교·분석하였다. 다만, MAD 검정 방법은 오른쪽 극치값만을 평가하는 것이 아니라 오른쪽 극치값에 상대적으로 더 큰 가중치를 주는 검정 방법으로 본 연구에서 RMSE, bias, MRD, MARD를 활용하여 오른쪽 꼬리 부분만 평가한 방법과 결과는 다소 다를 수 있으나, 어느 정도 비교척도로 사용가능할 것으로 판단된다.

모의실험결과 왜곡도 계수가 0.0과 +0.5 일때에는 NOR 분포가 다른 분포에 비해 오차의 값이 적게 추정되었다. NOR 분포는 정규분포로 왜곡도가 0인 특징을 가지고 있기 때문에 이와 같은 결과가 나온 것으로 해석할 수 있다. 왜곡도계수가 +1.0과 +1.5 일때에는 대부분 GUM 분포가 가장 오차가 적은 것으로 나왔으며, 왜곡도 계수가 +2.0과 +2.5일때에는 표본크기가 작을 때에는 GUM분포와 GLO분포가 오차가 적었지만, 표본크기가 클 때에는 RMSE, bias, MRD, MARD 모두 GEV 분포가 가장 오차가 적었다. 마지막으로 왜곡도 계수가 +3이상일 때에는 GLO 분포의 극치 수문량 추정능력이 가장 우수한 것으로 판단되었다.

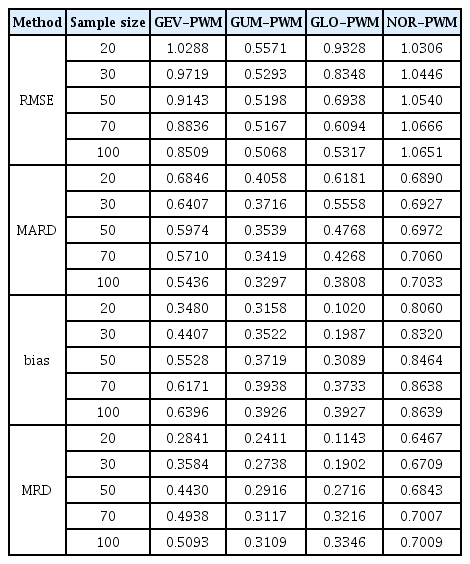
Tables 4∼7은 발생분포를 Wakeby로 하고 왜곡도계수가 각각 +0.5, +1.5, +2.5 그리고 +3.0 일 때 확률분포형에 적용하는 과정을 Monte Carlo 모의실험에 의해 1,000번씩 반복 수행하여 RMSE, bias, MRD, MARD 오차들의 평균값을 정리하였고 음영으로 된 곳은 오차의 평균이 가장 적은 곳을 표시한 것이다.

Table 4

RMSE, MARD, Bias and MRD for C_s = 0.5

Table 5

RMSE, MARD, Bias and MRD for C_s = 1.5

Table 6

RMSE, MARD, Bias and MRD for C_s = 2.5

Table 7

RMSE, MARD, Bias and MRD for C_s = 3.0

Fig. 2는 왜곡도계수에 따라 극치값에 가중치를 주는 MAD 검정 결과를 도시화 하였다. 가로축은 표본크기를 나타내고 세로축은 기각률을 나타낸다. 1에 가까울수록 기각이 가장 적게 된다는 뜻이며, 이는 발생된 자료를 잘 추정한 분포형이라고 할 수 있다. 왜곡도계수 0에 대해서는 실험하지 않았으며, 대부분의 MAD 검정 결과와 4가지의 평가방법의 결과가 일치하는 것을 확인 할 수 있다.

Fig. 2

Modified Anderson-Darling Test for C_s = 0.5 to 4.0

실제 표본자료의 왜곡도의 범위별로 각 적용 분포형의 확률수문량의 추정결과를 비교해보기 위해서 먼저 64개 지점을 대상으로 지속기간 24시간 자료에 대해서 왜곡도를 분석하였다. 분석결과 64개 지점의 지속기간 24시간 자료에서 0.14부터 3.81까지 다양한 왜곡도의 분포가 나타났으며, 영천지점이 0.14로 가장 낮았고 강릉지점이 3.81로 가장 높았다. 이후 모의실험과 같이 NOR, GUM, GEV, GLO 분포형을 적용하여 200년 빈도의 확률수문량을 추정하였다. 모의실험의 결과에서 각 왜곡도의 범위별로 가장 오차가 작은 분포형을 대표 분포형으로 가정하고 나머지 3개의 적용 분포형의 확률수문량과 비교하였다. 즉, C_s 0.5미만에서는 NOR 분포형을, 1.5미만에서는 GUM 분포형을 2.5미만에서는 GEV 분포형을, 마지막으로 4미만에서는 GLO 분포형을 대표 분포형으로 가정하고 나머지 3개의 적용 분포형의 확률수문량 값을 비교하였다.

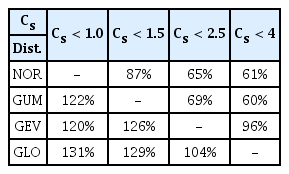
Table 8에서는 표본 자료의 왜곡도 범위 별 대표 분포형과 나머지 적용 분포형들간에 확률수문량의 비율을 정리하였다.

Table 8

Ratio of Estimation of Quantile with each Distribution for Duration 24hrs from 64 Sites

분석결과 C_s < 1.0의 지점들에서는 대표 분포형인 NOR분포형을 기준으로 적용 분포형 GUM, GEV, GLO 분포형 모두가 확률수문량을 크게 추정하였다. C_s < 1.5를 나타내는 지점에서는 GUM 분포형의 확률수문량을 기준으로 GEV와 GLO 분포형이 각각 26%와 29%씩 크게 추정되는 것을 확인하였다. C_s < 2.5의 지역에서는 GEV 분포형의 확률수문량을 기준으로 NOR과 GUM 분포형은 확률수문량이 작게 추정되었으며 GLO 분포의 경우 약간 높게 추정되었다. 마지막으로 C_s< 4인 지역에서는 GLO 분포형을 기준으로 나머지 3개의 분포형의 확률수문량이 모두 작게 추정되었음을 확인하였다. 이는 표본자료의 왜곡도 범위에 따라 여러 지점들의 200년 빈도에 해당하는 확률수문량의 증감율을 평균한 것이기 때문에 모든 지점에서 동일한 비율로 나타난다고 볼 수는 없지만 대체적으로 Table 8과 같은 비율로 나타나고 있음을 확인하였다. 대체적으로 동일 왜곡도의 표본을 대상으로 분포형별로 비교를 해보면 GLO, GEV, GUM, NOR의 순서대로 확률수문량이 추정되는 것을 확인 할 수 있었다. 이는 분포형의 특성으로 파악되며 GLO나 GEV 분포형의 경우 꼬리부분이 두껍게 형상화 되면서 상대적으로 GUM이나 NOR 분포형에 비해 동일 재현기간에 해당하는 확률수문량이 크게 추정되는 것으로 판단된다.

4. 결 론

본 연구에서는 확률분포형의 오른쪽 꼬리부분에 해당하는 극치 수문량 추정능력을 비교·분석하기 위하여 우리나라의 수문자료로부터 관측 될 수 있는 왜곡도 계수가 나타나는 다양한 표본크기의 자료를 Wakeby 분포로 발생시키고, 발생된 표본의 극치값과 추정하고자 하는 분포형의 극치수문량 값과의 오차가 가장 적은 분포형을 추정하기 위해 NOR, GUM, GEV, GLO 모형을 적용하였다. 추정량의 오차 분석 및 결과의 비교·분석을 위하여 네 가지(RMSE, bias, MRD, MARD)의 방법과 MAD 검정 방법을 각각 적용하였다. 모분포에 대한 왜곡도계수가 0과 +0.5일 때는 NOR 분포형이, 왜곡도계수가 +1과 +1.5 일 때는 GUM 분포형이, 왜곡도계수가 +2와 +2.5 일 때는 GEV 분포형이 가장 적합한 것으로 나타났다. 또한 왜곡도계수가 +3 이상일 때는 GLO분포형이 우수한 것으로 나타났으나, 표본 개수가 작을 때에는 왜곡도계수가 커도 GUM 분포가 가장 오차가 적음을 확인할 수 있었다. 왜곡도 0일 때를 제외한 나머지 결과에서는 RMSE, bias, MRD, MARD와 MAD 검정 방법이 유사한 결과를 나타냈으며 MAD 검정 방법 특성상 오른쪽 극치 부분만 검정하는 것이 아니라 오른쪽 극치 부분에 상대적으로 더 큰 가중치를 주고 검정하는 방법으로 표본크기가 작을 경우를 제외하고는 RMSE, bias, MRD, MARD의 결과와 대부분 일치하는 결과를 나타냈다. 이를 통해 본 연구에서 사용된 4가지 평가 기법의 적절성을 확인할 수 있었으며, 표본개수가 커질수록 오차의 크기가 작아짐을 확인 할 수 있었고, 왜곡도계수가 커짐에 따라 오차의 크기가 커짐을 확인 할 수 있었다. 64개 지점의 지속기간 24시간 자료에 대해서 모의실험과 같은 방법으로 각 분포형별로 확률수문량을 추정해 본 결과 GLO 분포형으로 확률수문량 추정시 가장 크게 추정되는 것을 확인하였다.

본 연구에서는 확률분포형의 극치 수문량 추정능력이 왜곡도계수와 표본크기에 따라 각각 다름을 확인하였으며, 이는 확률분포형을 선정하는데 있어 왜곡도계수 및 표본크기가 많은 영향을 끼치는 것을 확인할 수 있었다. 또한 점과 점의 오차를 나타내는 RMSE와 bias의 결과와 재현기간 사이의 사다리꼴 면적의 오차를 나타내는 MARD와 MRD가 서로 유사한 결과를 도출하는 것으로 분석되었다. 이를 통해 우리나라 수문빈도해석에서 오차의 척도로 많이 사용되는 RMSE와 bias 외에 좀 더 확장된 개념으로 2차원 면적 계산방식의 MARD, MRD 또한 오차를 판단하는 하나의 방법이 될 수 있을 것으로 판단된다. 본 연구에서 확인된 내용을 바탕으로 표본의 크기와 통계적 특성을 고려하여 보다 안정적인 확률수문량 추정을 수행한다면 국민의 안전과 재산을 보호하는 방재 및 치수분야에 널리 기여할 수 있을 것으로 기대한다.

Acknowledgements

본 연구는 행정안전부 극한 재난대응 기반기술개발사업의 연구비 지원(2017-MOIS31-001)에 의해 수행되었습니다.

References

Ahmad MI, Sinclair CD, Spurr BD. 1988;Assessment of flood frequency models using empirical distribution function statistics. Water Resources Research 24(8):1323–1328.

Alexandersson H, Førland EJ, Helminen J, Sjöblom N, Tveito OE. 2001. Extreme value analysis in the Nordic countries DNMI Report No. 03/01. KLIMA, Norwegian Meteorological Institute. Oslo, Norway:

Bartels H, Malitz G, Asmus S, Albrecht FM, Dietzer B, Gunther T, Ertel H. 1997. Starkniederschlagshöhen für Deutschland KOSTRA Atlas, Selbstverlag des Deutschen Wetterdienstes, Offenbach am Main.

Benson MA. 1962. Evolution of methods for evaluating the occurrence of floods USGS Water-Supply Paper, 1580-A. U.S. Geological Survey.

Bonnin GM, Todd D, Lin B, Parzybok T, Yekta M, Riley D. 2004. Precipitation-Frequency Atlas of the United States NOAA Atlas 14 (Vol. 2, Ver 2). National Wearther Serviece, Silver Spring. Maryland:

Greenwood JA, Landwehr JM, Matalas NC, Wallis JR. 1979;Probability weighted moments: Definition and relation to parameters of several distributions expressible in inverse form. Water Resources Research 15(5):1049–1054.

Haktanir T, Cobaner M, Gorkemli B. 2013;Assessment of right-tail prediction ability of some distributions by Monte Carlo analyses. Journal of Hydrologic Engineering 18(5):499–517.

Heo J-H, Kim K-D. 1995. A study of the selection of probability distribution for rainfall data in Korea. Journal of the Engineering Research Institute Yonsei University. 29(2)p. 193–200.

Heo J-H, Lee YS, Shin HJ, Kim K-D. 2007;Application of regional rainfall frequency analysis in South Korea(I) : Rainfall quantile estimation. Journal of the Korean Society of Civil Engineers 27(2B):101–111.

Heo J-H, Shin HJ, Nam WS, Om J, Jeong CS. 2013;Approximation of modified Anderson–Darling test statistics for extreme value distributions with unknown shape parameter. Journal of Hydrology 499:41–49.

Hogg WD, Carr DA, Routledge B. 1989. Rainfall intensity-duration-frequency values for Canadian locations Environment Canada, Atmospheric Environment Service.

Hosking JRM, Wallis JR. 1997. Regional Frequency Analysis Cambridge, UK: Cambridge University Press. 0521430453.

Hosking JRM, Wallis JR, Wood EF. 1984;Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 27(3):251–261.

Institute of Hydrology. 1999. Flood Estimation Handbook Wallingford, UK: Institute of Hydrology.

Landwehr JM, Matalas NC, Wallis JR. 1979a;Probability weighted moments compared with some traditional techniques in estimating Gumbel parameters and quantiles. Water Resources Research 15(5):1055–1064.

Landwehr JM, Matalas NC, Wallis JR. 1979b;Estimation of parameters and quantiles of Wakeby distributions: 1. Known lower bounds. Water Resources Research 15(6):1361–1372.

Lee JJ, Lee JS, Kim BI, Park JY. 2000;Derivation of probable rainfall formula of individual zone based on the representative probability distribution. Journal of Korea Water Resources Association 33(S1):124–129.

Maeng SJ, Lee SH, Lee HG, Ryu KS, Song GH. 2006;Flood frequency analysis by Wakeby and Kappa distributions using L-Moments. Journal of the Korean Society of Agricultural Engineers 48(5):17–27.

NERC (Natural Environment Research Council). 1975. Hydrological Studies. Flood studies report 1London: NERC.

Öztekin T. 2011;Estimation of the parameters of Wakeby distribution by a numerical least squares method and applying it to the annual peak flows of Turkish rivers. Water Resources Management 25(5):1299–1313.

Rahman A, Zaman MA, Haddad K, El Adlouni S, Zhang C. 2015;Applicability of Wakeby distribution in flood frequency analysis: A case study for eastern Australia. Hydrological Processes 29(4):602–614.

Rossi F, Fiorentino M, Versace P. 1984;Two-component extreme value distribution for flood frequency analysis. Water Resources Research 20(7):847–856.

Shin HJ, Jung YH, Jeong CS, Heo J-H. 2012;Assessment of modified Anderson-Darling test statistics for the generalized extreme value and generalized logistic distributions. Stochastic Environmental Research and Risk Assessment 26(1):105–114.

Shin HJ, Kim TS, Kim SY, Jung YH, Heo J-H. 2010. Derivation of the modified Anderson-Darling test statistics for the generalized extreme value and generalized logistic distributions. In : World Environmental and Water Resources Congress 2010: Challenges of Change. ASCE; p. 2371–2378.

Shin HJ, Sung KM, Heo J-H. 2010;Derivation of modified Anderson-Darling test statistics and power test for the Gumbel distribution. Journal of Korea Water Resources Association 43(9):813–822.

Singh V. 2012. In : Application of Frequency and Risk in Water Resources: Proceedings of the International Symposium on Flood Frequency and Risk Analyses; 14–17 May 1986; Louisiana State University; Baton Rouge, USA: Springer Science & Business Media;

Su B, Kundzewicz ZW, Jiang T. 2009;Simulation of extreme precipitation over the Yangtze River Basin using Wakeby distribution. Theoretical and Applied Climatology 96(3–4):209–219.

Thompson CS. 1992. HIRDS (Manual and software) New Zealand: National Institute of Water and Atmospheric Research.

Um MJ, Jeong CS, Lee TS. 2012;The optimal spatial analysis of precipitation in the region of Gangwon. J Korean Soc Hazard Mitig 12(1):179–192.

US Water Resources Council. 1976. Guidelines for determining flood flow frequency, Bulletin No. 17 Wasington D.C: U.S. Water Resources Concil.

Distribution	Cumulative distribution function	Range of random variable
GEV	F(x)=exp [-{1-β(x-μ)α}1β]	β = 0, GEV − 1: − ∞ < x < ∞ β < 0, GEV − 2: μ + α/ ≤ x < ∞ β > 0, GEV −3: − ∞ < x ≤ μ + α/β
GLO	F(x)=[1+{1-β(x-μ)α}1β]-1	β = 0, − ∞ < x < ∞ β < 0, μ + α/β ≤ x < ∞ β > 0, ∞ < x ≤ μ + α
GUM	F(x)=exp [-exp-{(x-μ)α}]	− ∞ < x < ∞
NOR	F(x)=12π∫-∞xexp[-12(y-μσ)2]dy	− ∞ < x < ∞

No.	Station	Skewness (min)	Skewness (max)	No.	Station	Skewness (min)	Skewness (max)
1	Sokcho	1.25	2.01	33	Jinju	1.38	2.64
2	Daeqwallyeong	1.21	2.48	34	Ganghwa	0.30	1.42
3	Chuncheon	0.02	1.15	35	Yangpyeong	0.88	1.31
4	Gangneung	2.09	3.81	36	Icheon	0.46	2.08
5	Seoul	0.56	1.26	37	Inje	0.63	1.87
6	Incheon	0.68	1.32	38	Hongcheon	0.58	1.28
7	Wonju	0.61	1.17	39	Taebaek	0.46	1.01
8	Ulleungdo	0.68	1.44	40	Jecheon	1.63	3.16
9	Suwon	1.06	1.59	41	Boeun	0.75	4.05
10	Chungju	0.95	1.70	42	Cheonan	1.03	2.02
11	Seosan	0.18	1.39	43	Boryeong	1.83	3.84
12	Uljin	0.25	1.04	44	Buyeo	0.09	0.91
13	Cheongju	−0.14	1.44	45	Geumsan	0.77	1.61
14	Daejeon	0.19	1.41	46	Buan	0.34	1.07
15	Chupungnyeong	0.55	1.76	47	Imsil	0.82	2.88
16	Andong	0.28	1.58	48	Jeongeup	−0.05	0.92
17	Pohang	2.20	3.78	49	Namwon	−0.08	2.31
18	Gunsan	1.23	1.85	50	Jangheung	0.70	2.65
19	Daegu	0.35	0.74	51	Haenam	0.69	2.40
20	Jeonju	0.45	1.20	52	Goheung	0.79	2.03
21	Ulsan	0.78	2.15	53	Yeongju	0.58	1.56
22	Changwon	0.28	1.33	54	Mungyeong	−0.01	0.82
23	Gwangju	0.47	1.77	55	Yeongdeok	1.03	2.13
24	Busan	0.65	1.33	56	Uiseong	0.16	1.54
25	Tongyeong	0.89	1.71	57	Gumi	−0.01	1.46
26	Mokpo	0.27	3.00	58	Yeongcheon	0.09	1.00
27	Yeosu	0.20	1.20	59	Geochang	0.28	0.87
28	Wando	1.13	1.53	60	Hapcheon	0.37	1.18
29	Suncheon	0.78	1.26	61	Miryang	0.61	1.19
30	Jeju	0.54	0.82	62	Sancheong	0.10	0.81
31	Seongsan	0.97	1.51	63	Geoje	0.08	1.78
32	Seogwipo	0.21	0.69	64	Namhae	0.24	1.19

Case	Parameters					Population statistics
Case	m	a	b	c	d	μ	σ	C_v	C_s	C_k
1	0	1	2.5	10.0	0.02	0.92	0.46	0.50	0.0	2.65
2	0	1	1.0	7.5	0.02	0.65	0.43	0.66	0.5	2.62
3	0	1	6.5	3.5	0.10	1.26	0.58	0.46	1.0	7.98
4	0	1	17.5	5.0	0.08	1.38	0.54	0.39	1.5	10.25
5	0	1	1.0	7.0	0.11	1.37	1.23	0.90	2.0	10.93
6	0	1	2.0	6.0	0.15	1.73	1.48	0.86	2.5	19.53
7	0	1	2.0	4.0	0.19	1.61	1.40	0.87	3.0	30.89
8	0	1	15.0	3.0	0.19	1.64	0.95	0.58	3.5	38.59
9	0	1	14.5	4.0	0.20	1.93	1.35	0.70	4.0	47.66

Method	Sample size	GEV-PWM	GUM-PWM	GLO-PWM	NOR-PWM
RMSE	20	0.2935	0.4627	0.4960	0.1691
	30	0.2386	0.4567	0.4553	0.1453
	50	0.1882	0.4556	0.4230	0.1182
	70	0.1540	0.4514	0.4058	0.1048
	100	0.1356	0.4502	0.4049	0.0937
MARD	20	0.4275	0.6468	0.6283	0.2860
	30	0.3513	0.6302	0.5715	0.2444
	50	0.2803	0.6199	0.5237	0.1959
	70	0.2303	0.6084	0.4953	0.1710
	100	0.2044	0.6035	0.4898	0.1506
bias	20	−0.1115	−0.3589	−0.3289	0.0667
	30	−0.0928	−0.3595	−0.3118	0.0672
	50	−0.0797	−0.3658	−0.3003	0.0628
	70	−0.0729	−0.3651	−0.2938	0.0632
	100	−0.0736	−0.3646	−0.2955	0.0640
MRD	20	−0.1844	−0.5835	−0.5026	0.1098
	30	−0.1567	−0.5843	−0.4779	0.1109
	50	−0.1381	−0.5951	−0.4623	0.1032
	70	−0.1281	−0.5938	−0.4530	0.1038
	100	−0.1298	−0.5930	−0.4560	0.1052

Method	Sample size	GEV-PWM	GUM-PWM	GLO-PWM	NOR-PWM
RMSE	20	1.0288	0.5571	0.9328	1.0306
	30	0.9719	0.5293	0.8348	1.0446
	50	0.9143	0.5198	0.6938	1.0540
	70	0.8836	0.5167	0.6094	1.0666
	100	0.8509	0.5068	0.5317	1.0651
MARD	20	0.6846	0.4058	0.6181	0.6890
	30	0.6407	0.3716	0.5558	0.6927
	50	0.5974	0.3539	0.4768	0.6972
	70	0.5710	0.3419	0.4268	0.7060
	100	0.5436	0.3297	0.3808	0.7033
bias	20	0.3480	0.3158	0.1020	0.8060
	30	0.4407	0.3522	0.1987	0.8320
	50	0.5528	0.3719	0.3089	0.8464
	70	0.6171	0.3938	0.3733	0.8638
	100	0.6396	0.3926	0.3927	0.8639
MRD	20	0.2841	0.2411	0.1143	0.6467
	30	0.3584	0.2738	0.1902	0.6709
	50	0.4430	0.2916	0.2716	0.6843
	70	0.4938	0.3117	0.3216	0.7007
	100	0.5093	0.3109	0.3346	0.7009