POT 방법을 이용한 극치 해수위의 비정상성 빈도해석
Non-stationary Frequency Analysis of Extreme Sea Level Using POT Approach
Article information
Abstract
본 연구에서는 극치 해수위의 비정상성을 반영하기 위하여 Peak-Over-Threshold (POT) 방법에 기초한 빈도해석이 수행되었다. 일반 Pareto 분포(GPD)의 매개변수들 중에서 규모 매개변수가 시간 의존적인 함수로 고려되었다. 부산지점이 연구대상지점으로 선정되었으며, 1976년부터 2015년까지 40년 동안 1시간 단위로 정리된 해수위 자료가 이용되었다. 연 최대치 시계열에 기초한 일반 극치 분포에 의해 추정된 재현기간별 극치 해수위 추정 값과 가장 유사한 결과를 얻을 수 있도록 POT 시계열의 임계값이 결정되었다. 정상성 GPD 모델과 비정상성 GPD 모델을 비교한 결과, 2055년에는 현재보다 재현기간 50년 극치 해수위 추정 값이 83 cm 정도 상승할 가능성이 많은 것으로 분석되었다.
Trans Abstract
In this study, frequency analysis based on the Peak-Over-Threshold (POT) method was performed to reflect the non-stationarity of extreme sea level. Of the parameters of the general Pareto distribution (GPD), the scale parameter was considered as a time-dependent function. The Busan site was selected as a study site, and sea level data from 1976 to 2015 (40 years) were collected at 1-hour intervals. The threshold value of the POT time series was determined to obtain extreme sea level estimates as close to those calculated by the generalized extreme value distribution based on the annual maximum time series. By comparing the stationary GPD model with the non-stationary GPD model, it was determined that the estimate of the extreme sea level for the 50-year return period is likely to be increased by approximately 83 cm in 2055.
1. 서 론
연안지역의 홍수 취약성을 살펴보고자 할 때, 극치 해수위에 대한 재현기간을 추정하기 위하여 빈도해석이 수행된다(Karamouz et al., 2014). 이 때, 빈도해석은 극한 현상의 발생확률을 결정하는 것과 관련이 있으며(Gilroy and McCuen, 2012), 어떤 변량의 초과 확률은 일반적으로 과거 관측된 자료의 극치분석에 의하여 추정된다(Mudersbach and Jensen, 2010). 극치 해수위의 빈도해석은 block maxima라고도 하는 연 최대 시계열(Annual Maximum Series, AMS)과 Peak-Over-Threshold (POT)의 두 가지 접근 방식을 기반으로 한다. AMS 방법은 확률분포를 정의된 시간 간격(주로 1년 단위)에 대한 해수위 최대치 자료에 적합시키는 반면에, POT는 특정 임계값 이상의 모든 독립된 극치 해수위를 선택하여 모형화한다(Lang et al., 1999; Silva et al., 2014). POT 방법에서는 특정 임계값의 정의가 매우 중요한 관심사항으로 부각된다(Li et al., 2012).
극치 해수위가 독립적이고(추정되는 확률분포의 매개변수는 독립적이고 동일하게 분포된 관측자료로부터 유도) 정상상태에 있다고 가정하면(극치 해수위에 영향을 미치는 모든 인자들이 과거 및 미래 어느 시점에서도 불변), Generalized Extreme Value (GEV) Distribution 분포와 Generalized Pareto Distribution (GPD)가 각각 AMS 및 POT 방법으로 선택된 극치 해수위 값에 대한 확률분포로 주로 적용되어왔다(Katz et al., 2002; Hawkes et al., 2008).
극치 해수위에 대한 독립성 가정은 관측자료를 추출하는 시간해상도를 적절하게 조정함으로써 정당화될 수 있으나, 관측자료의 평균 또는 분산에서 발견되는 추세성분은 정상성 가정의 유효성에 심각한 문제제기를 일으키고 있다(Khaliq et al., 2006). 대형 태풍사상에 의해 발생된 연안지역 극치 해수위 자료의 비정상성은 기후변화에 따른 변동성뿐만 아니라, 토지이용의 변화 및 연안지역 관리정책의 변화에 따라 복합적으로 작용하여 발생될 수 있다(Xiong and Guo, 2004; Milly et al., 2005; Ribereau et al., 2008; Salas and Obeysekera, 2014). 확률분포를 자료에 적합시키기 전에, 시계열에 포함되어 있는 비정상성의 여부를 평가하기 위한 추세를 사전에 점검할 필요가 있다(Jaiswal et al., 2015). 관측자료에 유의미한 비정상성이 포함되어 있을 경우에는 정상성 상태를 확보하기 위하여 이러한 비정상성은 반드시 제거되어야 한다(Salas, 1993). 그러나 빈도해석을 수행할 때 이와 같은 비정상성을 직접 고려하려는 시도들이 다수 수행되어왔다(Strupczewski et al., 2001; Villarini et al., 2009). 즉, 비정상성 빈도해석의 한 가지 장점은 관측자료가 추세성분을 가지고 있는 상태에서도 직접 적용될 수 있다는 것이다.
비정상성 빈도해석에서는 시간 의존적인 매개변수가 확률분포함수에 적용된다. 따라서 극치분석의 결과는 시간에 따라 달라진다. 비정상성 빈도해석을 수행하기 위하여 확률분포함수의 다양한 매개변수 형식이 제안되어왔다. 일반적으로 형상 매개변수는 상수로 가정되나(Lopez and Frances, 2013), 나머지 매개변수들, 즉 GEV 분포의 경우 위치 및 규모 매개변수는 시간 또는 공변량에 의존적인 것으로 간주된다. 비정상성 모델은 정상성 모델보다 더 정확한 결과를 제공하는 것으로 보고되고 있으며(Mendez et al., 2007), 지난 10여 년간 비정상성 모델의 성능이 크게 개선되고 있는 추세이다(Tramblay et al., 2013).
이에 본 연구에서는 연안지역 극치 해수위의 비정상성 빈도해석에 대한 방법론을 제공하는 것을 목표로 한다. 이를 위해 부산지점의 과거 극치 해수위 자료가 이용되었다. 잠재적인 추세성분을 감지하기 위해 일반적인 통계방법이 극치해수위 자료에 적용된다. POT 방법에 기초한 GPD가 미래의 극치 해수위를 추정하는데 적용된다. 또한 POT 방법에서 사용될 적절한 임계값을 선택하는 방법에 대한 논의가 수행된다. 최종적으로는 정상성 빈도해석의 극치 해수위와 비정상성 빈도해석을 통한 극치해수위가 서로 비교된다.
2. 연구방법
2.1 자료
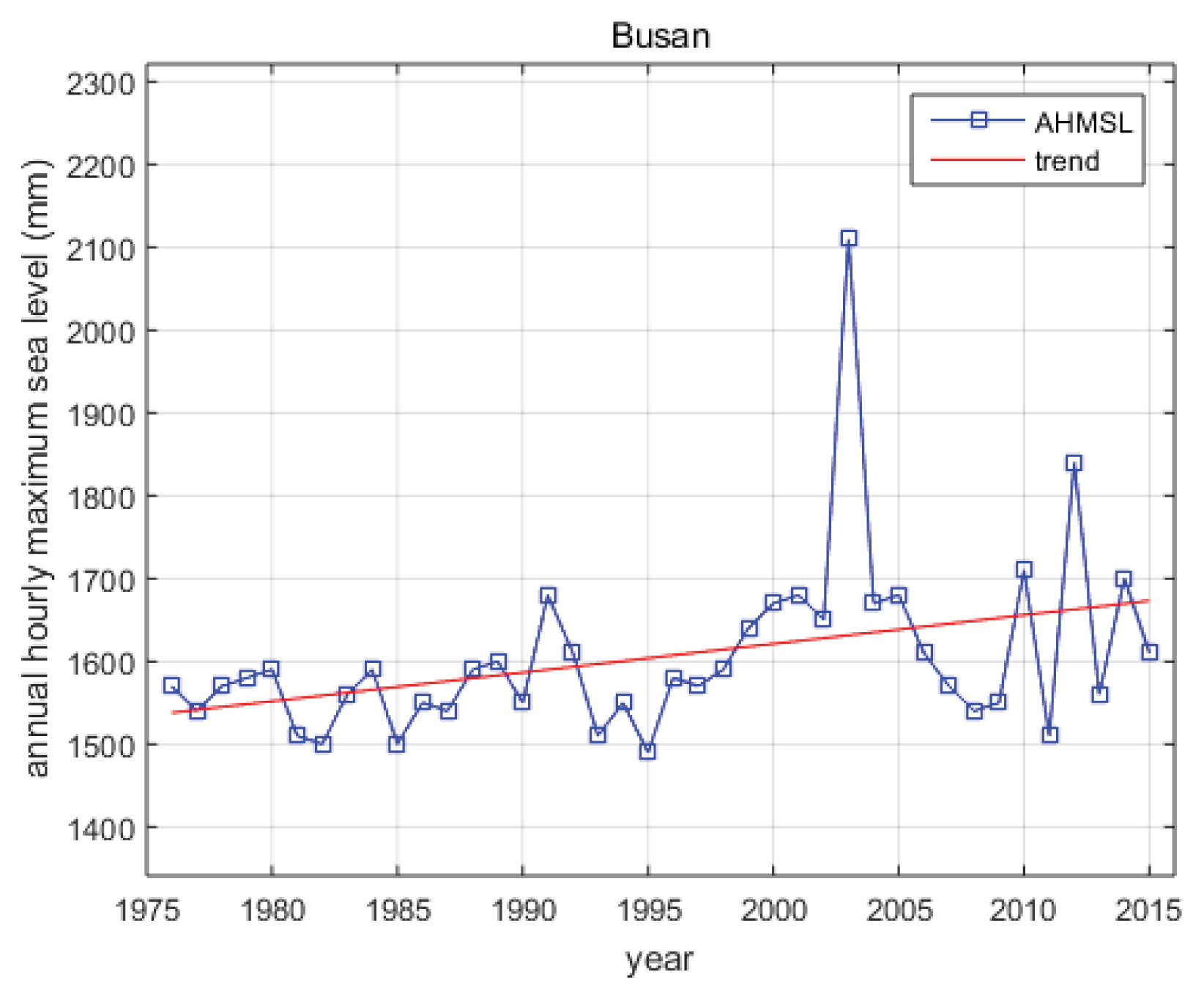
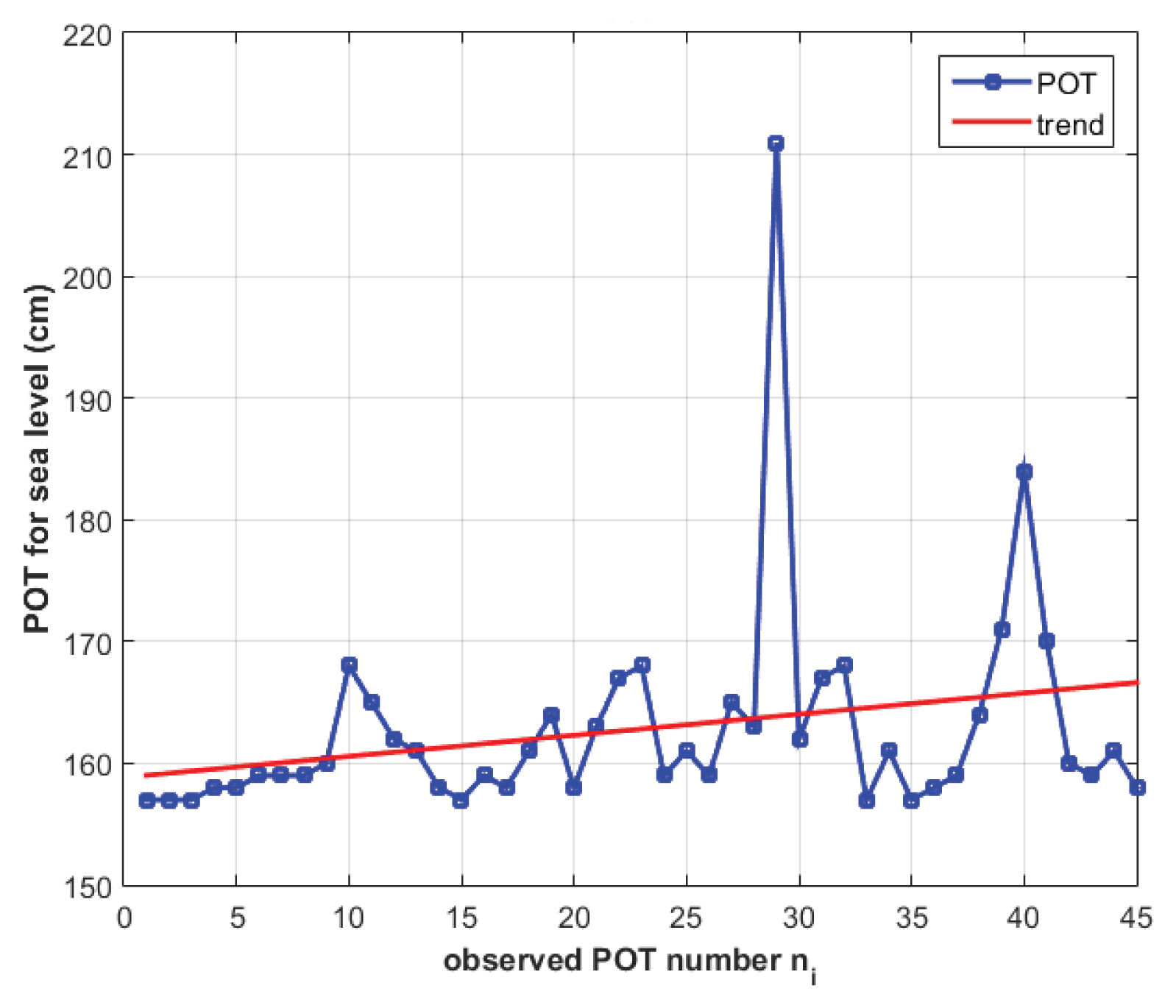
본 연구에서는 국립해양조사원(http://www.khoa.go.kr)에서 제공하는 부산지점의 1시간 과거조위자료를 사용하였다. 자료 기간은 1976년 1월 1일부터 2015년 12월 31일까지 40년이다. Fig. 1에서 사용된 자료의 연 최대 시계열(AMS)을 도시하였다. 부산지점의 극치 해수위 AMS는 강한 선형 추세가 있음을 살펴볼 수 있다. 연 최대치 시계열 중, 2003년의 극조위 211 cm (09.12)에는 태풍매미(0314)의 기상조(기상현상에 의하여 상승하강하는 조석성분) 72.8 cm, 2012년 극조위 184 cm (09.18)에는 태풍산바(1216)의 기상조 37.6 cm가 각각 포함되어 천문조(천체에 의하여 상승하강하는 조석성분)외에 부산인근에 직접적인 영향을 준 태풍에 의한 해수위 상승이 강하게 발생된 것으로 분석되었다. Fig. 1의 붉은 색 선은 극치 해수위 AMS를 단순 선형 회귀 분석한 결과로서, AHMSL (mm) = -5313.2317 + 3.4672 * year의 관계를 가지고 있으며, 기울기 3.4672 mm/year의 95% 신뢰구간은 0.64683 ~ 6.2875 mm/year으로 나타났다. 평균 해수위의 경우 대략적으로 2.5 mm/year의 상승률을 나타내는 것과 비교해보면, 극치 해수위 AMS의 경우 평균 해수위의 상승률을 상회하는 상승률을 보이고 있음을 살펴볼 수 있다. 극치 해수위 AMS의 Mann Kendall 경향성 분석 수행 결과, 추세가 없을 확률이 0.6634%로 나타났으며, AMS에서 단순히 선형 추세를 제거한 후에 Mann Kendall 경향성 분석을 수행하였을 경우에는 추세가 없을 확률이 52.16%로 나타났다. 따라서 부산지점 극치 해수위 AMS는 연도가 진행될수록 증가하는 경향성이 강하게 나타나는 비정상성 시계열임을 살펴볼 수 있다.
2.2 Generalized Pareto Distribution
GPD의 누가확률분포함수 F(x)은 Eq. (1)과 같이 정의된다(Hosking and Wallice, 1987).
여기서 확률변수 x의 범위는 xo<x<∞이며, α은 규모 매개변수, k은 형상 매개변수(k<0)이다. 임계값 xo은 사전에 결정되어야 한다. 이 때, 확률변수 x은 xo보다 큰 값을 갖게 되는데, x의 발생은 연간 발생률 λ로 설명되는 Poisson 분포를 따르는 것으로 가정된다. 연간 발생률 λ은 x >xo인 선택된 관측자료들의 개수를 관측 연수로 나눈 값으로 정의된다. 이 때, 선택된 자료들의 독립성을 보장하기 위하여 xo보다 큰 관측자료들이 연속적으로 선택되지 않도록 설정되어야 한다. 본 연구에서는 먼저 시간 조위자료 z로부터 일 최대조위자료 y을 구성한 뒤에 y>xo인 자료들 중에서 yt-1 < yt 및 yt≧yt+1인 자료만 선택하여 시계열 x을 구성함으로써 선택된 자료들의 독립성을 확보하고자 하였다.
여러 가지 방법들이 GPD의 매개변수를 추정하기 위하여 사용될 수 있으나, 본 연구에서는 추후 규모 매개변수 α가 시간 의존적일 경우에도 매개변수를 추정하기에 상대적으로 용이하다고 판단된 최우도법을 적용하였다. 매개변수들은 Eq. (2)과 같은 음의 대수 우도 함수(negative log likelihood) nllh을 최소화하는 최적화 기법을 이용하여 추정되는데, 본 연구에서는 매개변수 추정을 위한 최적화 기법으로 유전자 알고리즘이 이용된다.
여기서 n의 GPD에 적합되는 자료 개수이다. 매개변수들이 추정되고 나면, 재현기간 T-year에 대응하는 극치 해수위 xT은 Eq. (1)의 역함수를 구한 후, 연간 발생률 λ을 적용하여 Eq. (3)과 같이 계산될 수 있다.
전통적으로 GPD는 관측자료가 정상성을 가지고 있다고 가정하지만, 이 가정은 비정상성을 설명하기 위하여 매개변수들 중 하나 또는 두 개 모두가 시계열의 발생 순서에 의존적이라고 가정함으로써 완화될 수 있다. 즉, GPD 매개변수는 시계열의 발생순서에 따라 변하는 것으로 표현될 수 있다. 이론적으로 GPD의 모든 매개변수들이 시계열의 발생순서의 함수로 적용될 수 있으나, 본 연구에서는 Eqs. (4) ~ (6)의 형태를 갖는 규모 매개변수 α을 각각 적용되었다(Um et al., 2017).
여기서 ni은 시계열의 발생순서(1부터 n까지)이며, A, B, C은 Eq. (7)의 음의 대수 우도 함수를 최소화하는 과정에서 추정된다. 이로부터 도출되는 GPD는 시계열의 발생순서에 따라 다양한 분포형태를 갖게 된다.
비정상성 모델 1의 경우에는 규모 매개변수의 증가율이 시간이 흐를수록 감소되는 형태이며, 비정상성 모델 2의 경우에는 선형, 비정상성 모델 3의 경우에는 시간이 흐를수록 규모 매개변수의 증가율이 증폭되는 형태를 가진다.
정상성 GPD 모델과 비정상성 GPD 모델이 구성되며, 구성된 4개 모델들 중에서 Akaike Information Criterion (AIC)를 최소화하는 모델이 최적 모델로 선정된다. AIC는 Eq. (8)과 같이 계산된다(Akaike, 1974).
여기서 nllh은 정상성 모델의 경우에는 Eq. (2)을, 비정상성 모델의 경우에는 Eq. (7)로부터 결정되며, K은 모델의 매개변수의 개수로서 정상성 모델의 경우에는 K=2, 비정상성 모델 1의 경우에는 K=4, 비정상성 모델 2와 3의 경우에는 K=3이다.
3. 연구결과
3.1 임계값의 설정
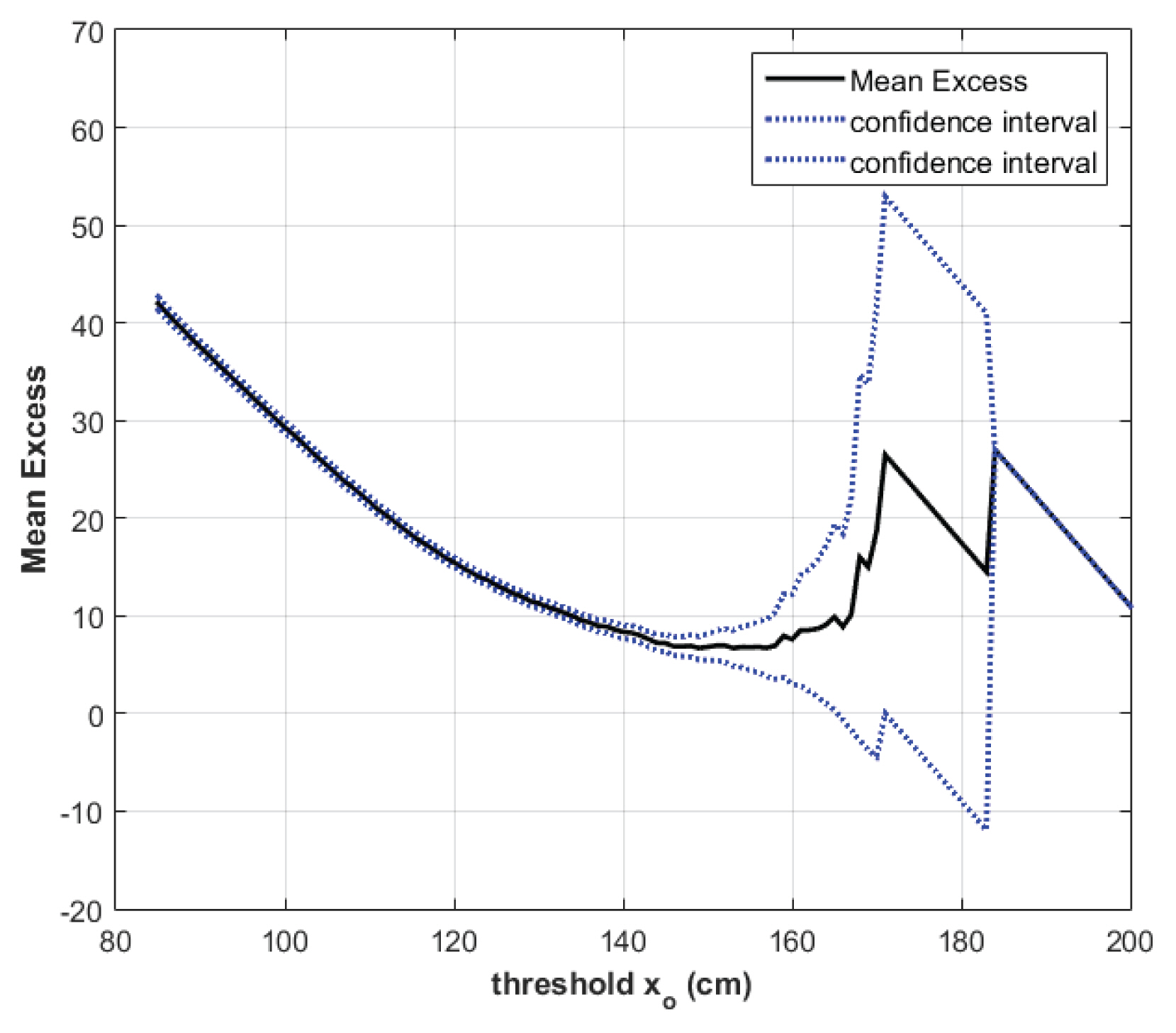
극치 해수위 자료를 해석하는 POT 접근방식에서는 특정 임계값 xo보다 큰 독립된 극치 해수위 자료를 선택하여 분석에 이용하기 때문에, xo의 설정이 매우 중요하다. 적절한 xo을 설정하는 방법들 중에서 가장 많이 이용되는 방법들 중 하나는 mean residual life plot이며(Coles, 2001), 이를 부산지점 해수위 자료에 적용한 결과를 Fig. 2에 도시하였다. 일반적으로 작은 xo에서는 비선형적인 곡선이 나타나며, xo가 증가하면서 대략적인 직선이 나타나게 되는데, 이러한 직선 구간에 있는 xo을 설정하는 것이 추천된다. Fig. 2로부터 적절한 xo의 범위는 대략 150~160 cm임을 살펴볼 수 있다.
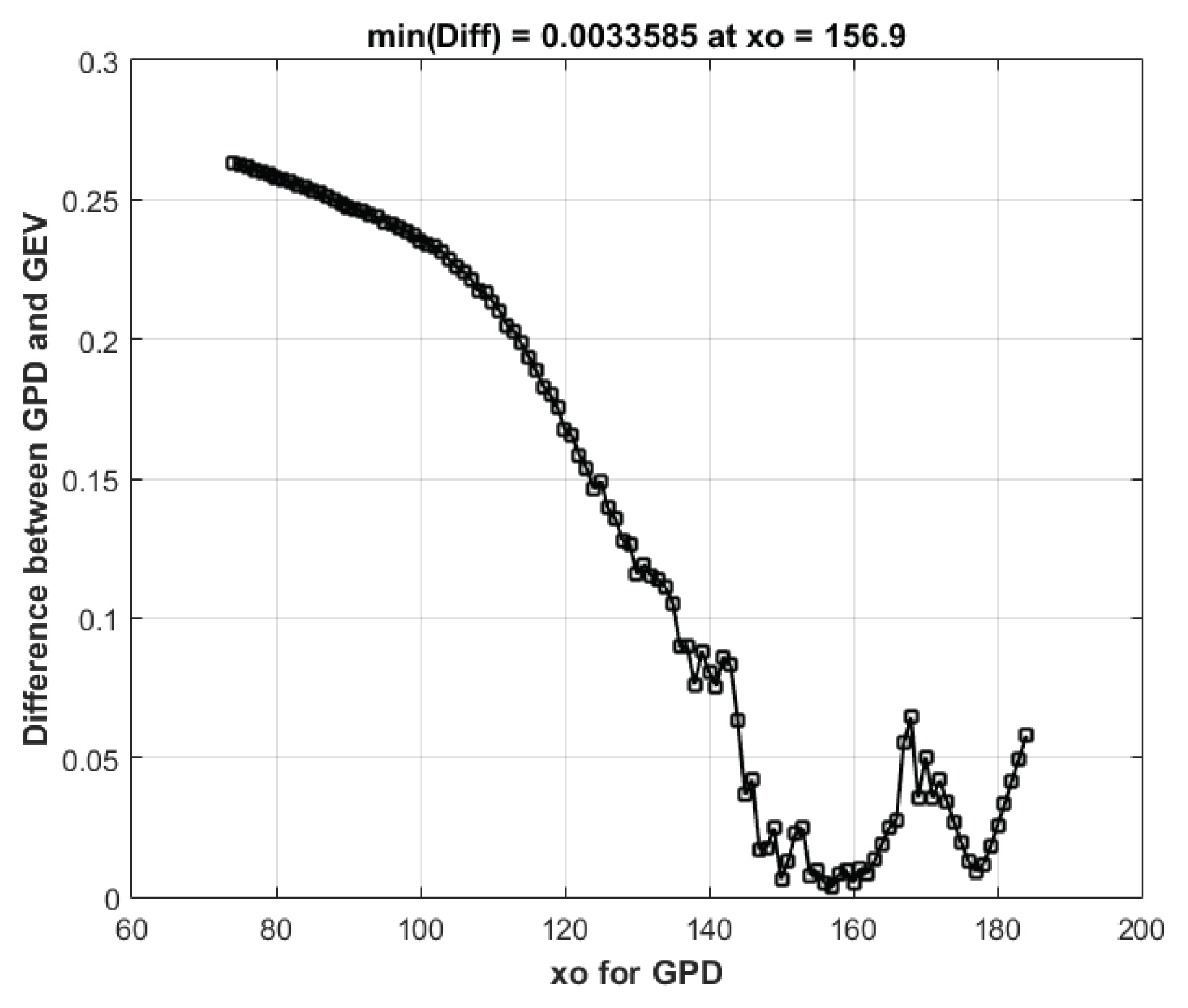
극치 해수위 빈도해석은 본 연구에서 적용하고 있는 POT 방법의 GPD 모델과 더불어서 AMS 방법의 GEV 모델이 주로 적용되므로, 본 연구에서는 연 최대 극치 해수위 자료를 GEV 모델(정상성 가정)에 적합시켜 도출한 재현기간별 극치 해수위 값들을 가장 잘 재현할 수 있는 임계값 xo을 설정하는 것이 타당할 것이라 판단하였다. 이에 다양한 xo을 적용하여 구축된 POT 시계열을 GPD 모델(정상성 가정)에 적합시켜 도출한 재현기간별 극치 해수위를 계산하였으며, 이를 AMS의 GEV 모델 결과와 비교하여 그 편차를 Fig. 3과 같이 도시하였다. 두 모델 사이의 편차 Diff은 아래와 같이 계산된다.
여기서
3.2 비정상성 빈도해석
임계값 xo = 156.9 cm를 적용하여 구성된 POT 시계열 x-xo을 Fig. 5에 도시하였다. Fig. 5의 붉은 색 실선은 POT 시계열의 선형 회귀 분석으로 도출된 선형 추세선으로, AMS와 마찬가지로 POT 사상의 발생순서에 따라 증가하는 경향성이 있음을 살펴볼 수 있다.
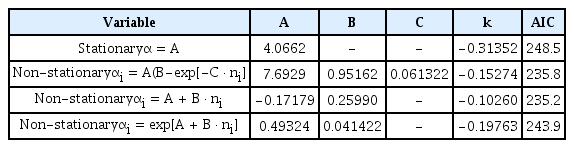
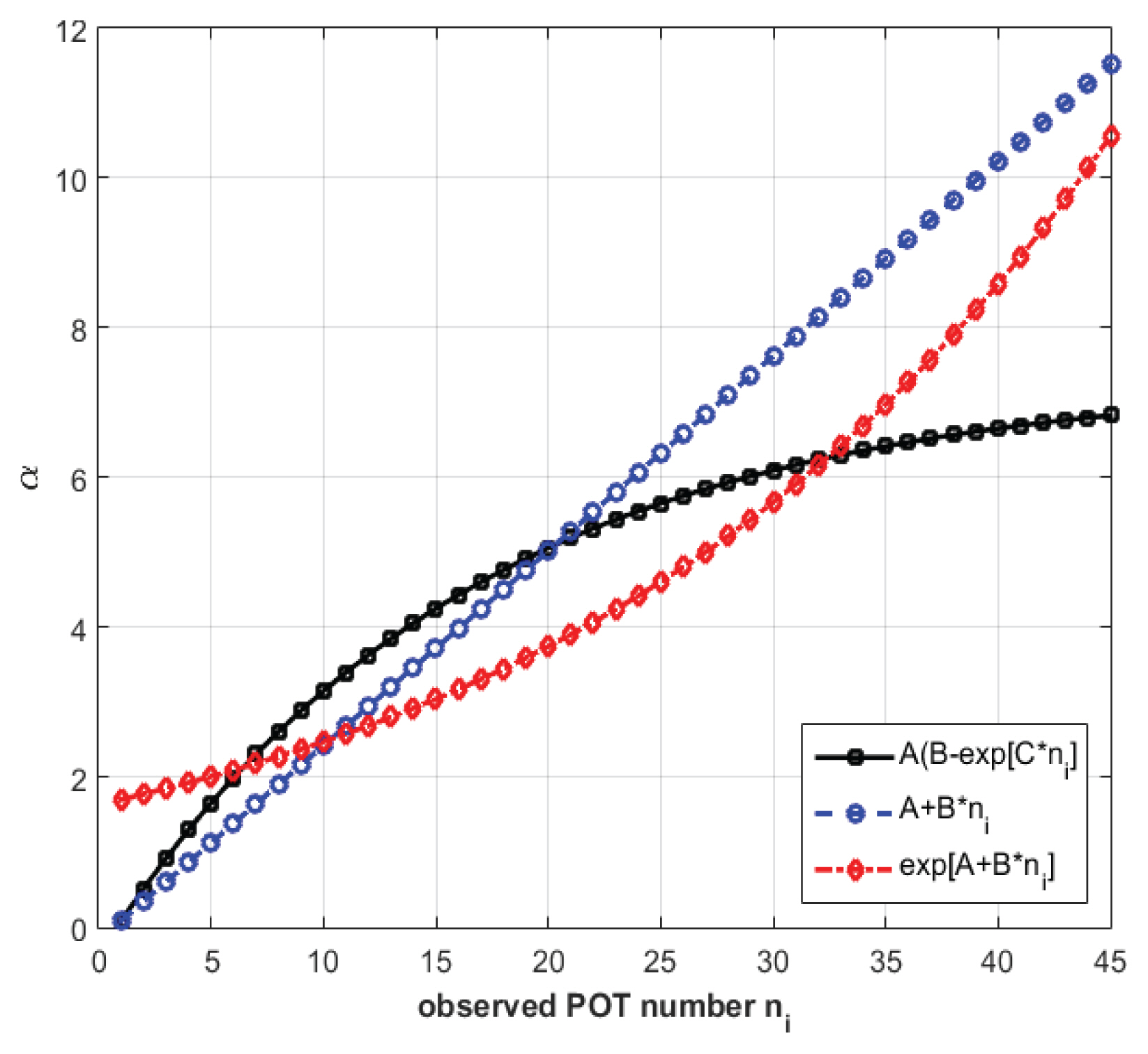
극치 해수위의 비정상성 빈도해석을 위하여 Eqs. (4) ~(6)과 같이 규모 매개변수를 시간 의존적인 함수로 구성한 GPD가 부산지점 극치 해수위 POT 시계열에 대하여 적합되었다. 정상성 모델과 비정상성 모델에 대한 매개변수와 AIC을 Table 1에 나타내었으며, Eqs. (4) ~ (6)의 형태로 추정된 규모 매개변수 α을 Fig. 6에 도시하였다. Table 1의 AIC 결과로부터 정상성 모델보다는 비정상성 모델이 부산지점 극치 해수위 자료를 더 잘 설명하고 있으며, 규모 매개변수를 선형으로 취할 때 더 우수한 모델이 구성되고 있음을 살펴볼 수 있다. 따라서 비정상성 모델 2를 이용하여 이후 분석을 수행하였다. Fig. 6의 규모 매개변수 α의 거동으로 볼 때 시간이 흐를수록 극치 해수위의 평균과 표준편차는 증가하고 있는 것으로 파악된다.
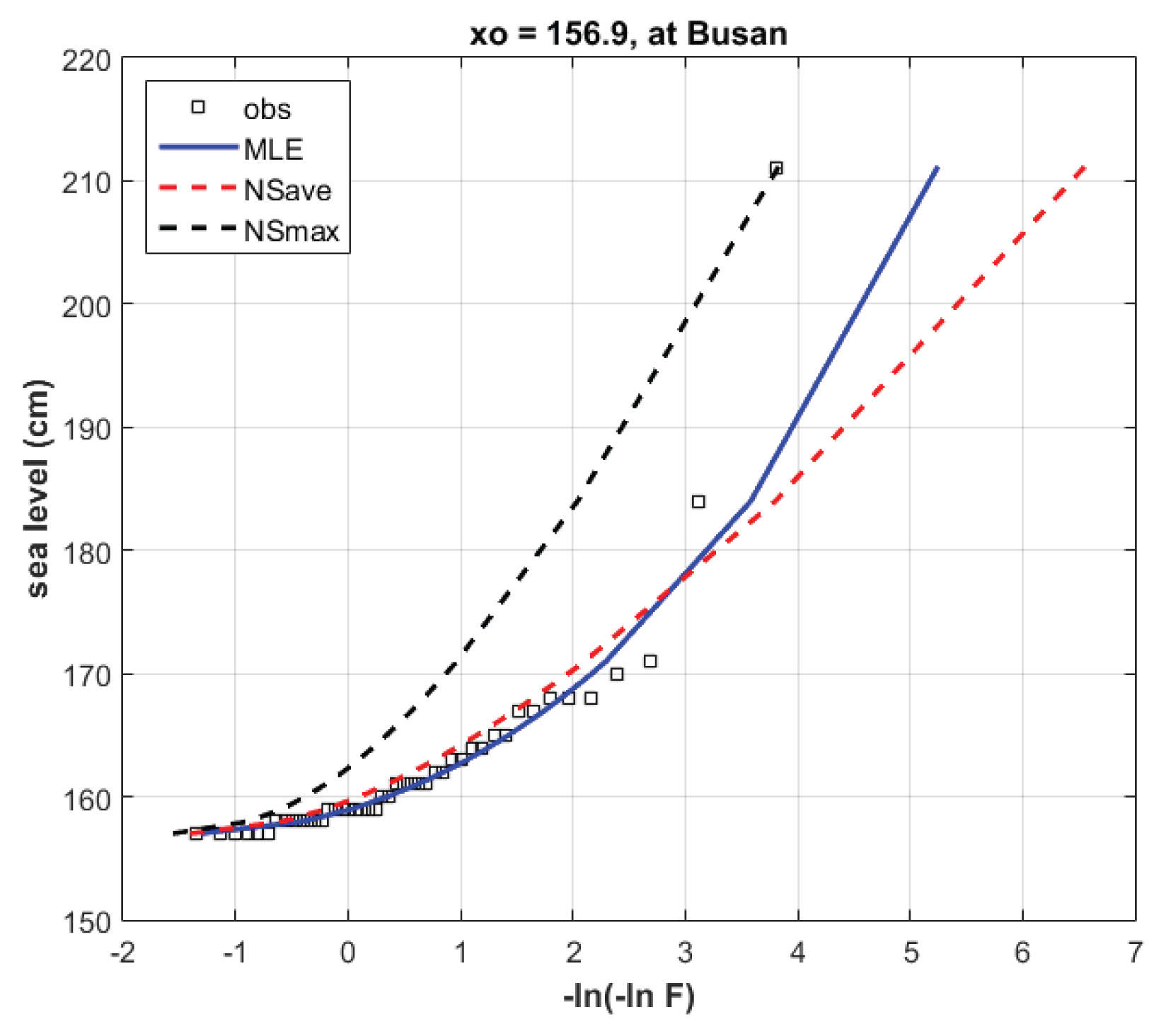
Fig. 7은 정상성 모델과 비정상성 모델의 누가확률밀도함수를 보여주고 있다. Fig. 7에서는 POT 시계열의 Weibull 공식을 적용한 경험적인 비초과확률이며, ‘MLE’은 최우도법을 이용하여 정상성 GPD 모델을 적합한 결과이다. ‘NSave’은 최우도법을 이용하여 비정상성 GPD 모델을 적합한 결과로서, 규모 매개변수 α에 ni = 23(사용된 POT 시계열의 전체 자료 수의 절반)을 적용하여 계산된 누가확률밀도함수이다. ‘NSmax’은 최우도법을 이용하여 비정상성 GPD 모델을 적합한 결과로서, 규모 매개변수 α에 ni = 45(사용된 POT 시계열의 전체 자료 수)를 적용하여 계산된 누가확률밀도함수이다. 재현기간 20년 이상(즉, Fig. 7에서 -ln (-ln F) > 3)에서는 ‘NSave’가 가장 작은 극치 해수위 추정 값을 제시하고 있으며, ‘NSmax’가 가장 큰 극치 해수위를 추정하고 있음을 살펴볼 수 있다. 이는 정상성 모델을 적용할 경우 최근 자료들이 추가될수록 재현기간별 극치 해수위 추정 값이 증가되는 경향과 부합하는 결과로 볼 수 있을 것이다.
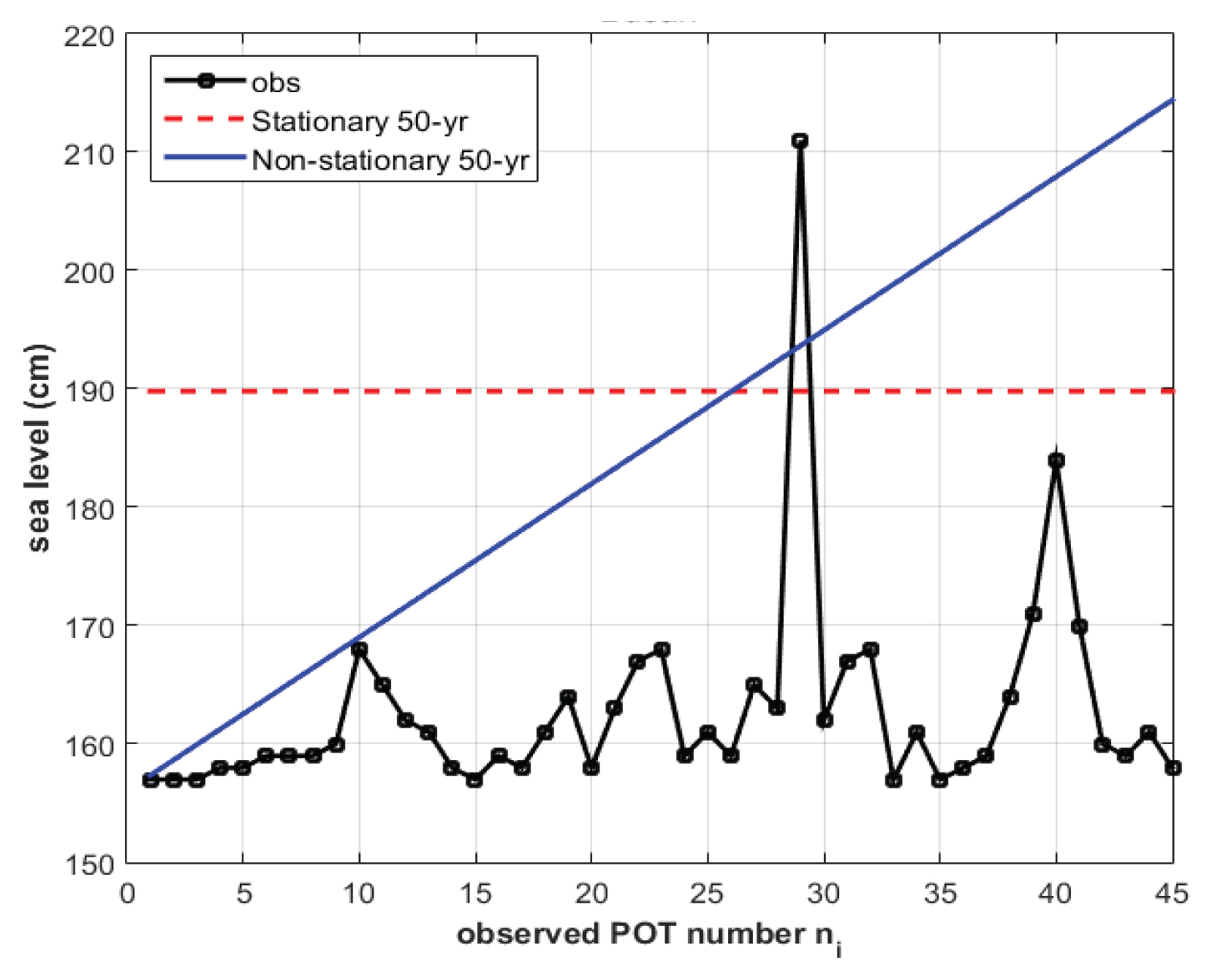
정상성 모델과 비정상성 모델의 결과를 서로 비교하기 위하여 비초과확률 98%, 즉 재현기간 50년에 해당하는 극치 해수위 추정 값을 Fig. 8에 관측자료와 함께 도시하였다. Fig. 8에서 ‘obs’는 관측된 극치 해수위 POT 시계열이다. 정상성 모델의 비초과확률에 대한 극치 해수위 추정 값은 시간에 따라 변하지 않으므로, 수평선으로 나타나게 된다(Fig. 8에서 점선). 반면에 비정상성 모델의 경우에는 시간에 따라 비초과확률에 해당하는 극치 해수위 추정 값이 변하는 형태를 갖게 됨을 살펴볼 수 있다(Fig. 8의 실선).
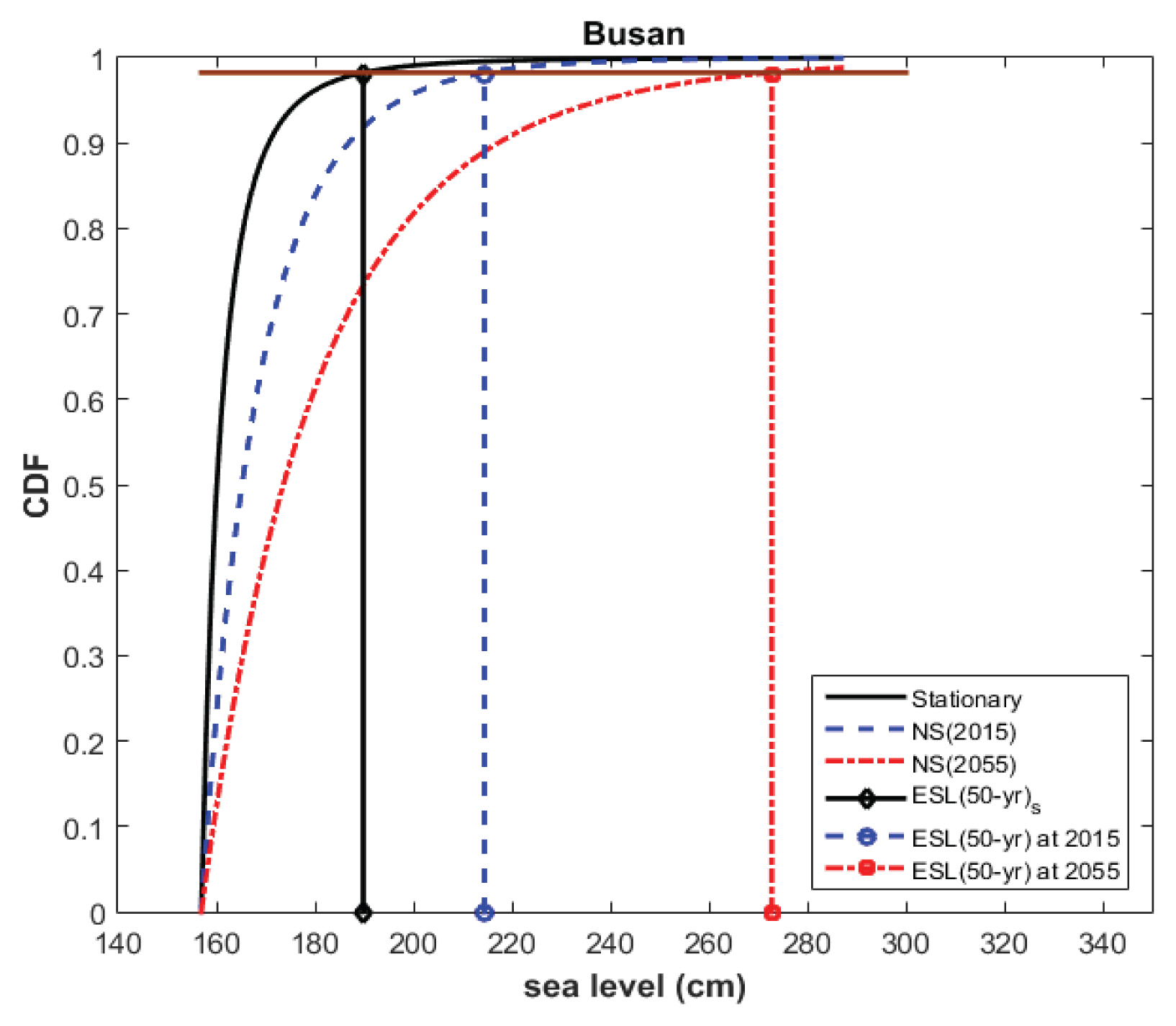
시간에 따른 극치 해수위의 변화는 관측자료의 마지막 연도인 2015년을 기준으로 추정된 비정상성 모델과의 확률밀도함수, 2015년 이후 관측기간 만큼의 미래 연도인 2055년을 기준으로 추정된 비정상성 모델의 확률밀도함수, 정상성 모델의 확률밀도함수 등을 서로 비교함으로써 더 명확하게 설명될 수 있다(Fig. 9 참조). 정상성 모델을 기준으로 미래로 갈수록 누가확률밀도함수가 우측으로 이동되고 있음을 살펴볼 수 있다. 이는 GPD의 규모 매개변수 α을 살펴보면 쉽게 이해될 수 있다. 정상성 모델의 규모 매개변수 값 4.0662를 기준으로 2015년 기준의 비정상성 모델의 규모 매개변수값은 11.5238이며, 2055년 기준의 비정상성 모델의 규모 매개변수 값은 23.2195이다. 자료가 GPD를 따를 경우 자료의 평균 및 표준편차가 커질수록 규모 매개변수가 커지기 때문이다. 즉, 본 연구에서 선택한 비정상성 모델의 경우 시간이 흐를수록 규모 매개변수가 커지는 형태이며, 이는 정상성 모델의 개념으로 보면 자료의 평균 및 표준편차를 증가시키는 역할을 하게 된다. 시간에 따른 규모 매개변수의 변화는 비초과확률에 해당되는 극치 해수위를 살펴볼 경우에도 명확하게 살펴볼 수 있다. Fig. 9에 도시한 바와 같이, 98% 비초과확률을 기준으로 정상성 모델의 극치 해수위는 189.8 cm이며, 2015년 비정상성 모델의 극치 해수위는 214.4 cm, 2055년 비정상성 모델의 극치 해수위는 272.8 cm임을 알 수 있다. 즉, 시간이 흐를수록 GPD의 규모 매개변수가 커짐에 따라 자료의 평균과 표준편차가 동반하여 증가하게 되므로, 재현기간별 극치 해수위 추정 값도 증가하게 된다.
확률밀도함수의 변화는 정상성 모델의 특정 비초과확률에 해당하는 극치 해수위을 초과하는 확률을 살펴봄으로써 정량화될 수도 있다. 예를 들어서, 정상성 모델에서 재현기간 10년 극치 해수위 추정 값은 171.6 cm이며, 이에 대응하는 초과확률은 10 %이다(Table 2 참조). 하지만 비정상성 모델에서는 2015년 기준과 2055년 기준에서 171.6 cm를 초과할 확률이 각각 30.1 %에서 54.1 %까지 변화될 수 있음을 살펴볼 수 있으며, Table 2에 제시된 재현기간 뿐만 아니라, 기타 여러 가지 재현기간에 대해서도 재현기간 10년에서의 결과와 유사한 결과를 얻을 수 있을 것이다.

Probability of Exceeding Stationary Quantiles for Stationary Model and for Non-stationary Model at 2015 and 2055
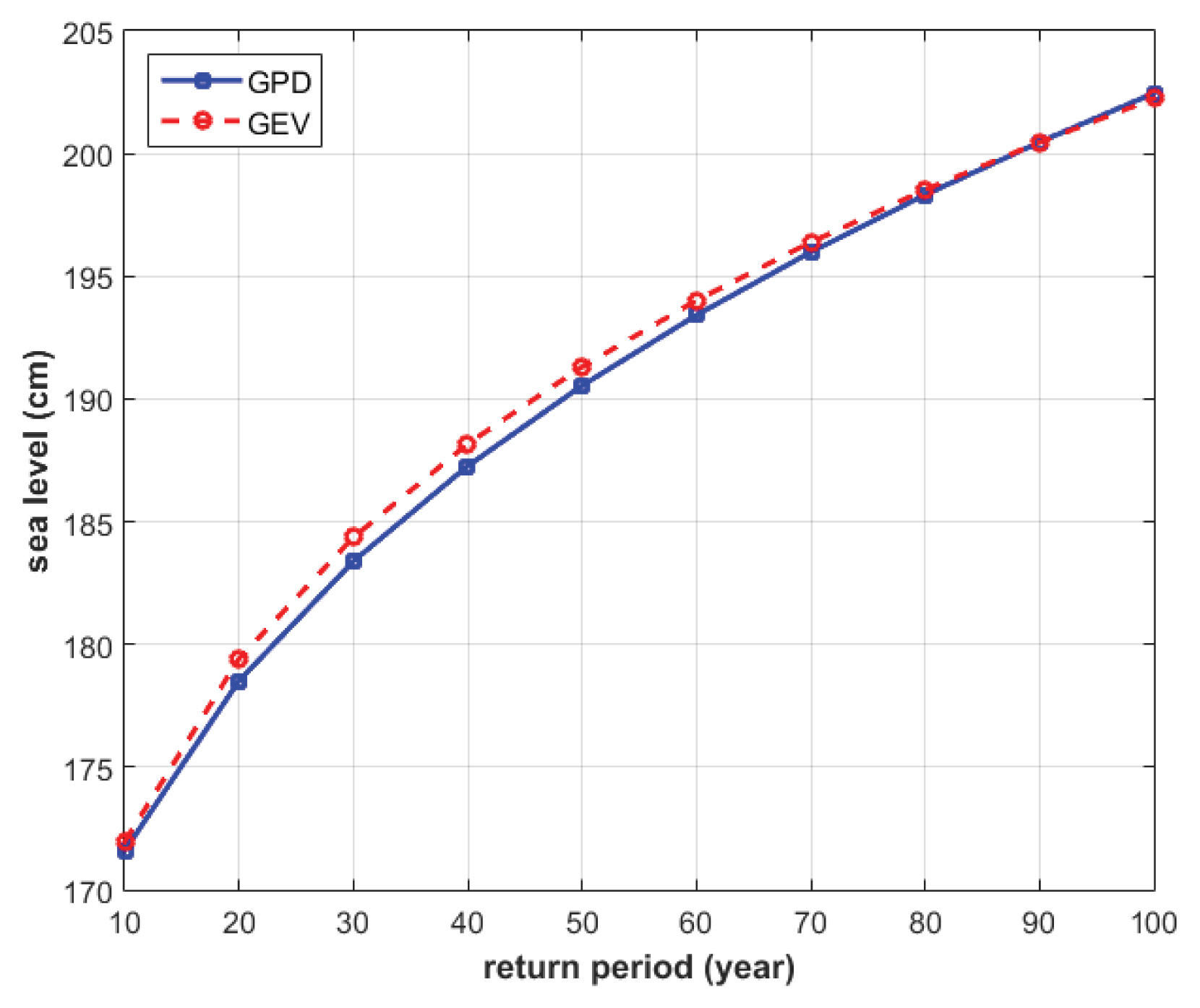
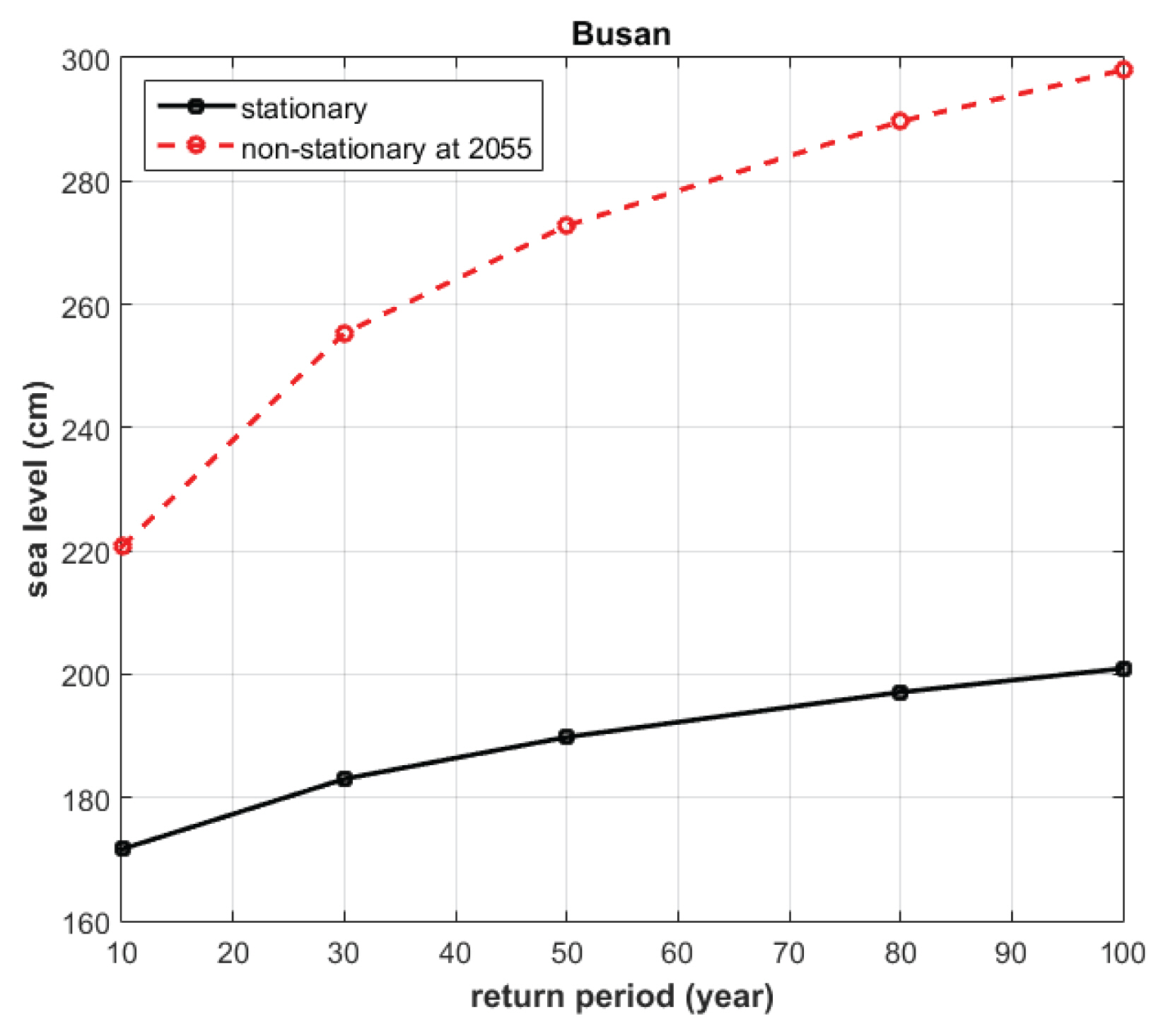
Fig. 10은 다양한 재현기간에 대응하는 극치 해수위 추정값의 변화를 도시하고 있다. 그림에서 실선은 정상성 모델에서의 재현기간별 극치 해수위 추정 값을, 점선은 미래 연도인 2055년 기준의 비정상성 모델에서의 재현기간별 극치 해수위 추정 값을 의미한다. 재현기간이 증가함에 따라 정상성 모델과 비정상성 모델의 편차가 증가하는 경향이 있으며, 재현기간 50년의 경우 83 cm 정도의 극치 해수위 추정값의 상승을 예상되고 있음을 살펴볼 수 있다.
4. 결 론
기후변화와 같은 자연환경변화는 관측자료의 정상성 가정에 상당한 영향을 미친다. 비정상성은 관측된 극치 해수위 자료의 빈도해석을 바탕으로 얻은 예상 설계 홍수위를 변경할 수 있기 때문에, 특히 연안지역의 연구에서 무시할 수 없다. 본 연구에서는 정상성 및 비정상성 모델을 부산지점의 극치 해수위 자료에 적용하였다.
연 최대치 시계열의 경향성 분석 결과, 자료의 비정상성이 확인되었으며 시간에 따라 연 최대치 시계열은 증가하는 경향을 보임을 살펴볼 수 있었다. 빈도해석을 위한 극치 해수위 자료는 POT 접근방식을 기반으로 선택되어졌다. POT 시계열을 추출하기 위한 임계값은 Mean residual life plot을 그려본 결과, 150 cm에서 160 cm 사이의 값이 적절한 것을 확인할 수 있었으며, 연 최대치 시계열의 빈도해석결과와 유사한 결과를 주는 임계값 156.9 cm를 최종 설정하였다.
자료의 비정상성을 반영하기 위하여 다양한 형태의 GPD의 규모 매개변수를 실험해본 결과, 선형함수의 형태가 가장 적절한 형태임을 알 수 있었으며, 정상성 GPD 모델과 비정상 GPD 모델의 AIC를 비교한 결과, 비정상성 GPD 모델이 POT 시계열에 더 잘 적합될 수 있음을 살펴볼 수 있었다. 선택된 모델을 이용하여 시간에 따른 극치 해수위 추정값을 분석한 결과, 부산지점의 경우 미래로 갈수록 재현기간별 극치 해수위 추정 값이 증가할 가능성이 매우 높음을 확인 할 수 있었다.
본 연구를 통해 시간 의존적인 확률분포형의 매개변수를 반영한 비정상성 빈도해석은 극치 해수위에 대한 기후변화의 영향을 살펴보기 위한 합리적인 방법이 될 수 있을 것으로 판단된다. 다만 본 연구에서는 GPD의 규모 매개변수를 시간의존적인 함수로 적용하여 연구를 진행하였으나, 추후 다양한 기후 및 해양 관련 공변량을 이용한 비정상성 모델의 적용 결과와 비교해 볼 필요가 있을 것이다. 또한 본 연구에서는 부산지점만을 대상으로 연구가 진행되었으나 추후 다양한 지점으로의 연구를 확장하여 결과를 비교하는 것이 바람직할 것으로 판단된다.
Acknowledgements
본 연구는 정부(행정안전부)의 재원으로 재난안전기술개발사업단의 지원을 받아 수행된 연구임[MOIS-재난-2015-03].