1. 서 론
구조물들은 건축됨과 동시에 노후화에 의해 내구도가 감소하게 되고 추가적으로 지진, 태풍과 같은 자연 재해에 의해 내구도가 추가적으로 감소할 수 있다. 일반적인 콘크리트 구조물의 경우 사용 연한을 50년에서 100년 사이로 예상하는 반면, 작은 손상이라도 긴 시간동안 겪게 된다면 구조물 건전도에 큰 변화를 줄 수 있다. 예상하지 못한 건전도 변화 후 보강 공사 없이 재난 현상을 겪게 될 시 심각한 문제로 발전 할 수 있기 때문에 사용 연한 동안 건축물의 변화를 감지하고 이를 보강해주는 방법들이 수행되고 있다(Farrar et al., 2006). 대표적인 구조물 변화를 관측하는 방법에는 육안 관측 방법과 비파괴검사 방법이 있다. 육안 관측은 구조물 내외부의 변화를 관측하여서 건전도(혹은 내구도) 변화를 인식하는 방법인데 구조물의 외관만 관측할 수 있다는 단점과 관측하는 사람에 따라서 결과에 대한 해석이 다를 수 있다는 두 가지 단점이 있기 때문에 중요한 구조물 일수록 내부의 변화를 측정할 수 있는 비파괴 검사 방법이 사용된다(Brownjohn et al., 2006).
다양한 비파괴검사 방법 중 대표적으로 구조물에 사용되는 방법은 음향 및 진동센서를 이용하는 것이다(Abdeljaber et al., 2017). 이러한 감지기들은 건축물이 건설되고 난 이후에도 설치가 가능하고 설치가 간편하기 때문에 많이 사용되고 있다(Grosse et al., 2006). 파괴로부터 발생된 신호는 건축물의 모양, 균열이 발생된 정도, 건축물의 구성 물질 등에 의해서 영향을 받아 전파되고 이를 감지기를 사용하여 수집하여 구조물 내부의 변화를 감지하는 연구가 다방면에서 진행되어 왔다(Ongpeng et al., 2018). 대표적으로 수집된 신호를 분석하는데 사용하는 방법으로는 신호 세기 분석, 도달 시간 분석, relaxation 분석, b-value분석 등이 있으며 이를 통하여 실험실 단위에서 균열의 발생 위치 및 균열의 크기, 내구도 등을 역으로 추정하는 방법에 관한 연구가 수행되어왔다(Sohn et al., 2003; Ohno and Ohtsu, 2010).
하지만 실제로 현장 구조물에 감지기를 설치하여 손상파괴 신호를 감지한 연구 사례는 수많은 실험실 결과와 다르게 찾기가 힘들다. 가장 큰 문제점은 실험실 스케일과 다르게 현장에서는 외력으로 인한 구조물 파괴 신호와 함께 구조물 진동으로 인한 노이즈, 활동으로 인한 노이즈 및 기계 동작으로 인한 노이즈 등의 다양한 노이즈가 파괴 신호와 함께 섞여서 수집되고 이렇게 섞여진 신호로는 파괴 신호의 발생을 감지하기가 힘들기 때문이다. 다양한 방식의 cross correlation과 몇 단계의 threshold 방법을 사용하여 노이즈가 섞여 있는 신호에서 파괴 신호를 감지할 수 있지만 이 또한 신호의 발생 위치가 명확하지 않거나 신호의 종류가 명확하지 않은 경우에는 사용될 수가 없다(ElBatanouny et al., 2014). 특히 현장에서는 현존하는 필터를 사용하였을 때 요구 전력량이 커지게 되고 이는 실시간 감지 능력을 떨어트리게 된다(Pandya et al., 2013).
이에 본 연구에서는 노이즈 신호와 파괴신호가 섞여서 수집될 경우 1차적으로 손상파괴 신호(비정상 신호)가 포함되어 있는 신호만을 특정해주는 기계학습 모델을 개발하였다. 이때, 노이즈 신호는 콘크리트 구조물 내에서 인간 활동으로 인해 발생될 수 있는 다양한 노이즈 신호를 수집하였고, 손상파괴 신호는 콘크리트 시편의 일축압축파괴 실험을 통해 수집하였다. 이후 일정 범위의 SNR을 유지하여 무작위로 합성하여 현장 신호 조건을 모사하였다. 기계 학습 모델로써 1차원 합성곱신경망(1D Convolutional Neural Network, 1D CNN)을 사용하여, 손상파괴 신호가 포함된 신호만을 선별하는 모델을 개발하였다. 우선 학습데이터 셋을 이용하여 모델을 학습시킨 후, 학습에 경험한 신호들의 구별하는 정확도를 분석하고, 그 후 학습에 경험치 못했던 신호를 시험함(표준화)으로써 정확도를 도출하였다. 개발된 방법론 및 기계학습모델은 구조물 스마트 모니터링 기법에 적용함으로써 현장에서 구조물 손상 진단 방법에 효과적으로 사용될 수 있고, 특히 전체적인 신호처리과정의 부하를 줄여 주는 효과가 있을 것이다.
2. 신호 수집
2.2 노이즈 신호 수집
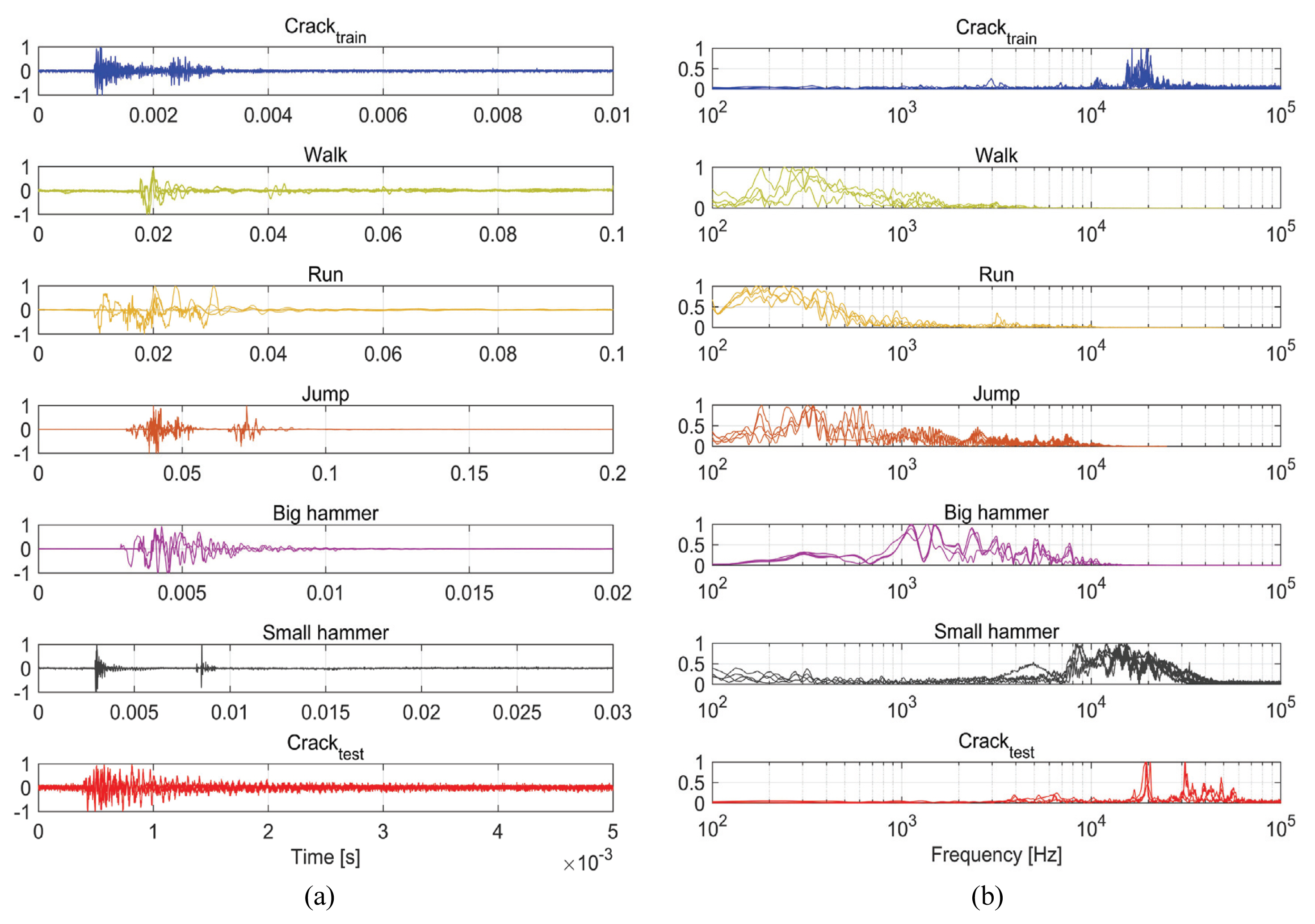
일반적으로 건물 내외부에서 발생할 수 있는 노이즈 종류는 매우 다양하다. 그중 가장 대표적인 인공적 인체 활동으로 인한 노이즈를 건물 내부에 가속도계를 부착하여 수집하였다. 추가적으로 물체를 낙하하거나, 기계 활동으로 야기 될 수 있는 노이즈 신호들을 수집하였다. 인체 활동으로 인해 발생되는 소음들의 경우, 주파수 대역이 낮은 편이다. 따라서 손상파괴 신호와 비슷한 주파수 대역을 가지는 소음을 추가하기 위해 해머로 두드리는 소음을 추가적으로 수집하였다. Fig. 2에서 학습 및 검증에 쓰이는 손상파괴 신호와 노이즈 신호를 보여주고 있다.
3. 신호 합성
3.1 학습 및 검증 셋 합성
수집된 손상 파괴 신호와 노이즈 신호는 신호 표준화를 위해서 가공 처리되었다. 신호 표준화는 에너지의 차이를 없애기 위해서 평균을 0으로 만들고 단위 분산을 가질 수 있도록 가공하였다. 신호 합성 전에 기계학습 모델의 학습을 위한 학습 데이터 세트와 이를 검증하기 위한 검증 데이터 세트로 각기 나누어 주었다. 학습 데이터 세트는 손상파괴 신호 100개와 노이즈 신호 464개의 원본 신호를 사용했으며, 검증 데이터 세트는 손상파괴 신호 32개와 노이즈 신호 236개를 사용하였다. 이때 나누어지고 난 뒤에는 표준화 검증 과정의 정당성을 위해 검증 데이터는 학습에 전혀 사용되지 않는다.
신호 합성은 데이터 편중을 없애기 위해서 손상파괴 신호의 합성 여부, 손상파괴 신호와 노이즈 신호 번호, 손상파괴 신호의 합성 위치를 랜덤 함수를 통해 결정해서 합성하였다. 합성을 통해 총 5개의 학습 및 검증 세트를 만들었고 각기 세트 별 학습 신호 2,500개와 검증 신호 500개로 구성되어 있다.
3.2 신호 대 잡음비 조정
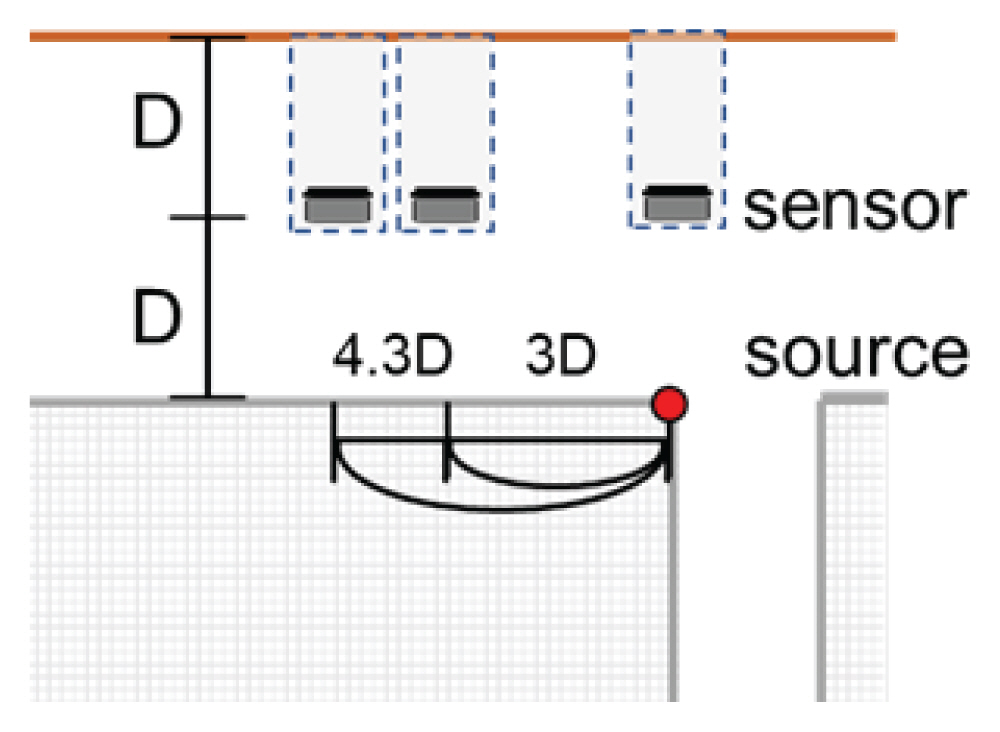
신호 대 잡음비(Signal to Noise Ratio, SNR)는 현장 신호 수집에서 중요한 인자이다. SNR = 0을 기점으로 그보다 낮은 경우에는 threshold를 통한 분석이 불가능하고 이러한 경우 cross-correlation 등을 통해 신호를 분석하는 시도 등이 있어왔다. 같은 구조물 내에서 감지기를 통해 전달되는 노이즈와 파괴 신호의 거리에 따라 신호의 세기가 차이 난다. 이를 개략적으로 나타내기 위해서 노이즈의 세기를 손상파괴 신호의 세기의 1, 10, 20배로 만들어서 신호 합성을 진행하였다. 건축물의 기초에 중심부에 감지기가 설치되었다고 가정 했을 때를 기준으로 각 신호 대 잡음비가 가지는 거리를 대략적으로 Fig. 3에 표현해 두었다.
서로 다른 SNR 범위를 가지는 학습 데이터를 합성하기 위해서 표준화된 노이즈 신호와 파괴 신호를 합성하기 전 신호 세기비의 제곱근을 곱해주는 방식을 취한다. 마찬가지로 통제된 비율대로 합성이 되고 난 이후에는 다시 신호 표준화 과정을 거쳐서 신호들끼리 표준성을 맞춰준다. 마찬가지로 검증을 위한 데이터 또한 신호 대 잡음비를 –13 데시벨의 범위까지 데이터를 합성하였다.
4. 기계학습 모델의 학습 및 검증
4.1 모델 디자인
학습에서 사용된 모델의 구조는 Table 2에 올려 두었다. Table 2에 사용된 모델의 구조와 함께 입출력 크기를 함께 올려두었다. 입력 데이터는 감지기에서 수집된 신호 중 진폭 데이터만을 사용하였다. 감지기에서 신호가 수집 될 때 샘플링 레이트에 따라서 진폭과 동시에 시간이 함께 기록이 된다. 현재 사용된 데이터의 길이는 10,000으로 1 ms 단위의 샘플링 레이트로 수집 되었을 때 총 신호 수집 시간은 0.01초가 된다. 신호의 간격이 동일하게 맞춰진 상태에서는 신호마다 시간에 대한 정보가 동일하기 때문에 단순히 10,000개의 진폭으로만 이루어진 데이터를 입력 데이터로 사용하였다. 학습 신호의 경우는 2,500개의 데이터가 한 셋을 이루고 있고 검증 신호는 500개가 한 셋을 이루고 있다. 이에 학습데이터는 한번에 25,000,000개의 데이터가 입력 데이터로 들어가게 되고 검증 신호는 5,000,000개의 데이터가 입력 데이터로 들어가게 된다. 또한 출력 값으로는 손상파괴 신호가 포함된 신호의 경우 1, 손상파괴 신호가 없는 신호의 경우 0으로 정하였다. 이러한 최종 출력 값을 만들어 주기 위해서 모델의 마지막 부분에 댄스 모델을 사용하여서 선형 패턴에서 단 하나의 값으로 수렴 시켜서 하나의 숫자로 출력 되게 하였다. 본 연구에서는 Table 2에서 볼 수 있듯이 입력 값이 임베딩, 1D convolution, max pooling, global max pooling을 거쳐서 최종 출력 값인 1과 0으로 표시되게 된다. 특히, 사용된 모델중 대표적인 역할을 하는 임베딩 모델과 1D 합성곱 모델에 대한 설명을 추가하였다.
4.1.1 Embedding
임베딩은 기계 학습에 입력된 데이터들을 벡터화 하는 역할을 수행한다. 기계 학습의 모든 데이터는 필수적으로 벡터화를 필요로 하는데 이때 사용되는 가장 단순한 방법이 원핫인코딩이다. 이는 0과 1로 숫자를 표현하는 방법인데 예를 들어 0부터 10까지 11개의 숫자를 표현하는 경우 데이터 길이가 11인 0으로 이루어진 데이터에서 1을 표현할 때는 2번째 숫자만 1로 4를 표현 할 때는 5번째 숫자만 1로 바꿔서 표현하는 방법이다. 이 경우 10,000개의 스칼라 숫자들을 표현하기 위해서는 10,000자리의 원핫인코딩이 필요하다. 반면 임베딩을 사용한 벡터화를 통해서 이를 100개로 축소시킬 수 있다. 임베딩을 통해 벡터화를 시키는 과정은 다음과 같다. 우선 전체 데이터들을 임의의 방법으로 배치를 한다. 이때 모델 내부에서 자체적인 방법에 의해서 배치를 하게 되고 임의의 방법으로 배치되는 경우의 수는 사용자에 의해서 결정 될 수 있다. 데이터들이 임의로 배치될 때 데이터들은 임의의 방향성을 가지게 된다. 초기 배치된 방향에서 학습을 진행하면서 의미가 있는 방향만이 가중치를 통해서 보상을 받게 되고 이를 통해 실제로 의미가 있는 방향들을 학습하기 시작한다. 최종적으로는 실제로 데이터의 의미 자체를 모델이 이해 할 수는 없지만 연구에서 필요한 목적에 맞게 데이터들이 분류되는 현상을 볼 수 있다. 최종적으로는 원핫인코딩보다 간결한 결과를 도출 할 수 있다.
4.1.2 1D convolution
1차원 합성곱(1D convolution)은 기계학습에서 다양하게 사용되는 모델이다. 1차원 합성곱이 본 연구에 적용되는 방법은 다음과 같다. 입력 데이터의 길이가 10,000일 때 일정 사이즈의 커널이 순차적으로 입력 데이터에 곱해지고 곱해진 결과가 출력 데이터가 된다. 순차적으로 곱해지는 커널의 간격은 사용자에 의해 결정된다. 순차적으로 곱해지는 커널에 의해서 출력된 데이터는 커널의 특성에 따라서 특정 패턴이 존재하는 부분이 강조된다. 학습이 진행되면서 균열이 있는 부분을 찾아주는 방향으로 커널이 보상을 받게 되고 이를 통해 최종적으로 균열이 있는 패턴을 강조시켜 줄 수 있도록 파라미터들이 보정된다. 커널의 사이즈에 맞추어서 작은 사이즈의 커널을 통해서는 짧은 구간에서 패턴이 강조되고 큰 사이즈의 커널을 통해서는 긴 구간에서의 패턴이 강조된다. 이에 커널 사이즈를 강조 하고자 하는 구간의 크기와 비슷한 사이즈로 맞추어 주었을 때 가장 용이하게 학습이 진행된다. 또는 본 연구의 모델에서와 같이 1차원 합성곱을 여러 개 쌓으면 작은 사이즈의 커널을 사용하여도 긴 구간의 패턴 또한 강조할 수 있다. 커널 사이즈가 작기 때문에 1차적으로는 짧은 구간의 패턴이 강조되지만 여러 개의 층을 거치게 되면서 짧은 구간들 사이의 패턴이 강조되게 되고 이를 통해 긴 구간의 패턴 또한 관측 할 수 있다.
4.2 학습 모델 검증 결과
디자인된 모델을 사용하여서 학습을 진행 한 후 학습이 된 모델을 사용하여서 정확도를 검증하였다. 정확도는 전체 신호의 개수 중에서 파괴 신호를 파괴 신호(비정상 신호)로 옳게 검증한 개수와 비파괴 신호(정상 신호)를 파괴 신호가 아니라고 옳게 검증한 개수의 합의 비율로 나타내었다. 기계 학습을 통해서 검증된 데이터의 정확도를 표현하는 방식은 여러 가지 방식이 있다. 옳은 데이터를 찾는 게 중요한 경우는 전체 정상신호 중 검증을 통해 분류한 정상 신호의 개수의 비를 사용하고 오답률이 중요한 경우에는 정상신호로 분류된 신호 중 정상 신호가 아닌 비율을 사용하여서 정확도를 평가한다. 본 연구는 다수의 신호에서 비정상 신호가 포함된 신호를 중앙처리장치에 보내주는 것도 중요하지만 비정상 신호가 포함된 신호를 정상 신호로 오답을 내는 경우를 줄이는 것 또한 중요하기 때문에 보수적으로 정확도를 설정하였다. 본 연구에서 목표로 설정한 정확도는 80%로 80%이상의 정확도가 나온 경우에 성공으로 판정하였다. 이는 80%까지 정확도가 나온 다면 이는 우연에 의해서 나올 수 없고 학습에 의해서 나온 결과로 판단 할 수 있기 때문에 학습 검증을 위해서는 충분한 정확도이기도 하고 80% 이상으로 정확도를 올리기 위해서는 모델을 더 깊이 쌓아야 하는데 이를 통해서 얻는 결과들의 시간 소요가 커지기 때문이다.
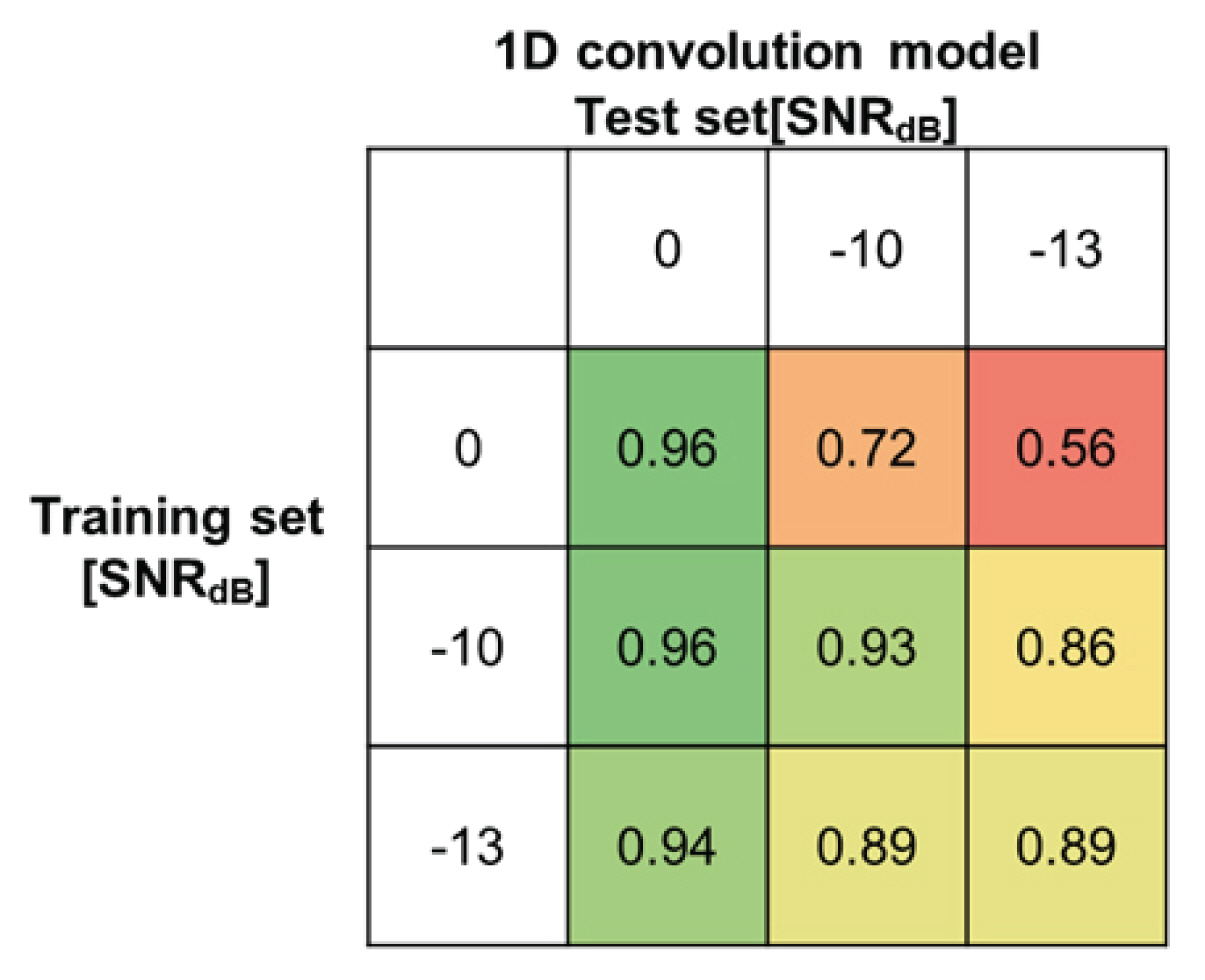
고정된 감지기 위치에서 수집된 신호에 검증 한계 거리 정보를 주기 위해서 SNR을 바꿔서 데이터 검증 셋을 만들고 이를 통해 검증을 하고 실제로 감지기에 기학습된 모델을 적용할 때 목표 정확도를 가질 수 있는 데이터 합성법에 대한 정보를 주기 위해서 각 SNR별로 데이터 학습 셋을 만들어서 모델을 학습하기 때문에 Fig. 4와 같은 매트릭스 형태로 정확도 결과가 나오게 된다.
Fig. 4는 검증 데이터로 분류된 데이터 셋을 사용하여 정확도를 구해본 결과이다. 학습과 검증에서 사용된 정상 신호가 동일한 장소에서 동일한 방법을 통해서 수집되었고 학습과 검증에서 사용된 비정상 신호가 동일한 콘크리트 공시체가 일축압축 실험에 의해서 부서지면서 수집된 신호이다. 이러한 경우 학습과 검증에서 사용된 신호는 동일한 신호는 존재하지 않지만 전체적으로 비슷한 양상을 보인다. 이에 Fig. 4에서 보이는 정확도는 본 연구와 유사한 실험에서 1차원 합성곱이 보여줄 수 있는 한계 정확도에 대한 정보를 담고 있다. Fig. 4에서 볼 수 있듯이 3가지 다른 SNR로 학습 시킨 모델에서 공통적으로 SNRdB가 0인 경우는 검증이 용이함을 볼 수 있다. SNRdB가 0인 경우는 threshold 방법을 통해서도 유사한 결과를 얻을 수 있다. 하지만 threshold 방법을 사용할 수 없는 SNRdB –13의 노이즈가 목표 신호의 세기보다 20배가 큰 경우에도 두 모델에서 정확도를 80% 이상 얻을 수 있다.
4.3 표준화 검증 결과
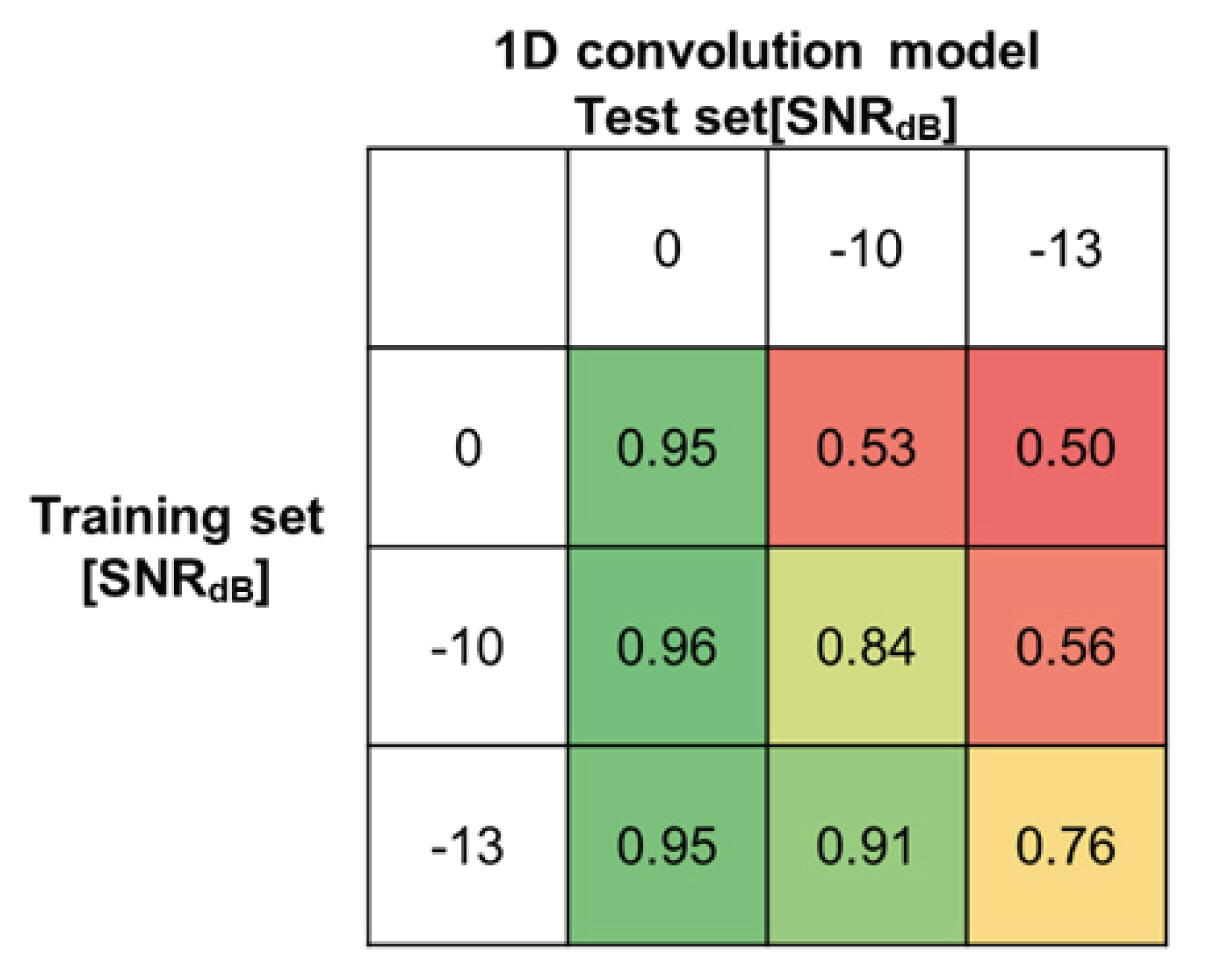
기계 학습을 통해서 학습시킨 모델을 검증하는 과정에는 표준화 검증 결과가 필수적이다. 학습에 사용된 데이터와 완전히 다른 학습으로 경험하지 못한 데이터를 시험하였을 때 정확성과 예측성능이 보장될 경우, 범용적으로 사용 가능한 모델임을 입증할 수 있다. 따라서 학습 과정에서 전혀 사용하지 않고, 학습한 손상파괴 신호와 전혀 다른 새로운 신호들을 사용하여 검증 데이터 세트를 만들었다. 이를 기학습된 모델에 적용하여 정확도를 도출하고 이를 Fig. 5에 나타내었다.
Fig. 5에서 학습 및 검증에서 사용된 파괴 신호는 서로 다른 콘크리트 공시체를 일축 압축 실험을 통해서 파괴하면서 수집된 신호이기 때문에 신호가 전체적으로 유사성이 매우 떨어지게 된다. 이에 표준화 데이터 세트를 사용할 경우, 전체적으로 정확도가 학습데이터 세트들에 비해 감소하는 것으로 나타났다. 여전히 SNRdB 0인 데이터에서는 세 모델 전부 학습이 성공하였지만 SNRdB –10의 검증 데이터는 두 개의 모델에서만 성공하였고 –13에서는 어느 모델도 학습을 성공하지 못하였다. SNRdB –13으로 학습된 경우에는 학습이 진행되었지만 결국 목표 정확도인 80%를 달성하지 못 하였다. 학습 데이터를 사용한 검증 결과와 다른 결과가 나오는 이유는 명백하다. 다른 배합비로 조성된 콘크리트 시료에서는 파괴 신호의 양상이 바뀌기 때문으로 판단된다. 하지만 고무적인 것은 전혀 새로운 샘플로부터 나온 신호이지만 –10까지 손상파괴 신호를 구별 할 수 있는 것으로 나타났다. 이는 서로 다른 배합 비를 사용하여서 파괴신호를 수집하였기 때문에 세세한 부분에서는 신호의 유사성이 떨어지지만 콘크리트가 파괴가 되면서 나오는 신호라는 점에서는 공통적인 부분을 가지고 있기 때문에 검증이 가능한 것으로 판단된다. 이를 통해서 본 연구에서 실험실에서 얻은 데이터를 사용하여서 학습 및 검증을 진행하였지만 파괴 신호라는 전체적인 특성을 모델을 통해 학습이 가능하였던 것으로 보아 본 연구를 통해서 학습된 모델은 범용적으로 다른 현장에서도 유사한 방법으로 적용 가능하다고 판단된다.
5. 결 론
본 연구에서는 콘크리트 구조물 내부에서 손상균열이 발생 되었을 때 이를 감지하기 위해서 사용되는 음향 및 진동 진단기에서 수집된 신호에 균열 신호뿐만이 아닌 노이즈 신호가 함께 섞여서 수집되는 일반적인 경우에 균열 신호가 포함된 신호를 구별 해 주는 알고리즘을 학습하여 이를 통해 표준화 결과까지 나타내었다. 추가적으로 유사한 연구를 진행하는데 도움이 될 수 있도록 데이터 수집, 합성, 모델 구성, 학습, 검증에 이르기까지 결과를 얻을 때까지의 과정을 전체 다 설명하였다. 특히 목표 신호와 노이즈가 다양한 세기로 합성 될 때 목표 신호를 검증하기 위해서 학습 셋의 신호 세기 설정 방법과 또 이를 통한 한계 구분 세기에 대한 연구를 진행하였다. 표준화 데이터 셋을 통한 검증을 추가적으로 진행함으로써 모델의 표준성을 확보 하였다. 본 연구에서 1차원 합성곱 모델을 적용하여 비정상 신호를 구분해본 결과 일반 검증 셋에서는 SNRdB –13까지 구분이 가능하고 표준화 검증 셋에서는 SNRdB –10까지 구별이 가능하였다. 본 연구에서 개발된 알고리즘을 사용하면 노이즈가 섞여 있더라도 파괴 신호가 들어가 있는 신호만을 특정 해줌으로써 이를 통해 전체 시스템의 부하를 줄일 수 있을 것으로 생각된다. 또한 동일한 방법으로 학습을 진행하였을 때 목표로 하는 신호만 바꿔서 데이터를 가공한다면 다양한 곳에서 목표로 하는 신호만을 찾아주는 간단한 필터를 만들 수 있을 것으로 생각된다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
Print
