1. 서 론
이상기후와 지구온난화로 인하여 최근 집중호우의 빈도 및 강도는 증가하고 있다. 국내 산지지형은 경사가 급하고 계곡의 길이가 짧기 때문에, 산사태에 취약할 수밖에 없다. 산사태의 평균 발생 면적은 1970년대부터 증가하고 있으며, 이러한 현상은 집중호의의 발생 빈도와 매우 밀접하게 관련 있음을 보여준다. 산사태로 인한 사망자의 수는 연평균 58명이며, 최근 감소추세지만, 우면산 산사태 또는 마적산 산사태와 같은 대규모 산사태가 발생하고 있다. 또한 Korea Forest Research Institute (2014)에 따르면 산지의 농작지화로 인하여 이러한 산사태의 증가추세는 앞으로 계속될 것이라고 예측하고 있다. 국내에서 산사태는 대부분 토석류로 연결되기 때문에(Kim, 2002), 산사태의 이러한 추세는 토석류에도 적용될 수 있다. 토석류는 전파길이가 길고, 이동속도가 매우 빠르기 때문에, 많은 사태(avalanche) 중 가장 위협적으로 인식되고 있다(Shin, 2014). 토석류의 피해를 줄이기 위해서는 토석류의 거동(behavior) 메커니즘을 정확하게 파악하는 것이 선행되어야 할 것이다. Iverson (1997)은 토석류의 거동을 움직임(mobilization), 운동(motion or moving) 그리고 퇴적(deposit) 3단계로 구분하였으며, 일반적인 토석류 거동특성은 이와 같이 분류된다. 움직임은 토석류가 발생하는 시작부분으로써, 간극수압의 복잡한 변화가 이 과정에 포함된다. 이에 따라 토석류의 유동특성을 예측하는 많은 모델들은 이 과정에 대해 수치적으로 예측하기 쉽지 않다. 이에 따라 다양하고 많은 토석류 유동 모델들이 토석류의 운동을 정확하게 예측하는 것에 집중하였다(Luna et al., 2012; Jakob et al., 2013; Zhou et al., 2013; Rengers et al., 2016). 반면에, 토석류의 퇴적에 대한 정확한 예측 모델은 상대적으로 많지 않다. 이에 토석류의 운동에 있어서 정확도가 검증된 Urban Debris Simulator (UDS)를 이용하여, 토석류 퇴적에 대한 수치모의 정확도를 확인하였다.
퇴적의 과정은 토석류 선단부에 위치한 상대적으로 큰 파편들의 운동량이 저하되면서 시작된다(Major, 1996; Iverson, 1997). 파편들의 정지는 연쇄적으로 뒤따르던 토석류 물질들의 정지로 연결되며, 이러한 연속적인 과정을 통해 퇴적이 발생된다(Major, 1997). 초기 큰 파편들의 운동량 감소는 지형적인 영향을 크게 받기 때문에, 어떠한 모델의 퇴적 메커니즘에 대한 정확한 재현 여부는 지형적 영향이 거의 없는 평평한 지형에서 발생된 퇴적 자료와의 비료를 통해 수행되어야 한다. 이에 USGS 토석류 수로(USGS debris flume)에서 수행된 Major (1997)의 실험을 이용하여 UDS의 검증을 수행하였다.
2. 이론적 배경
2.1 Major의 실험
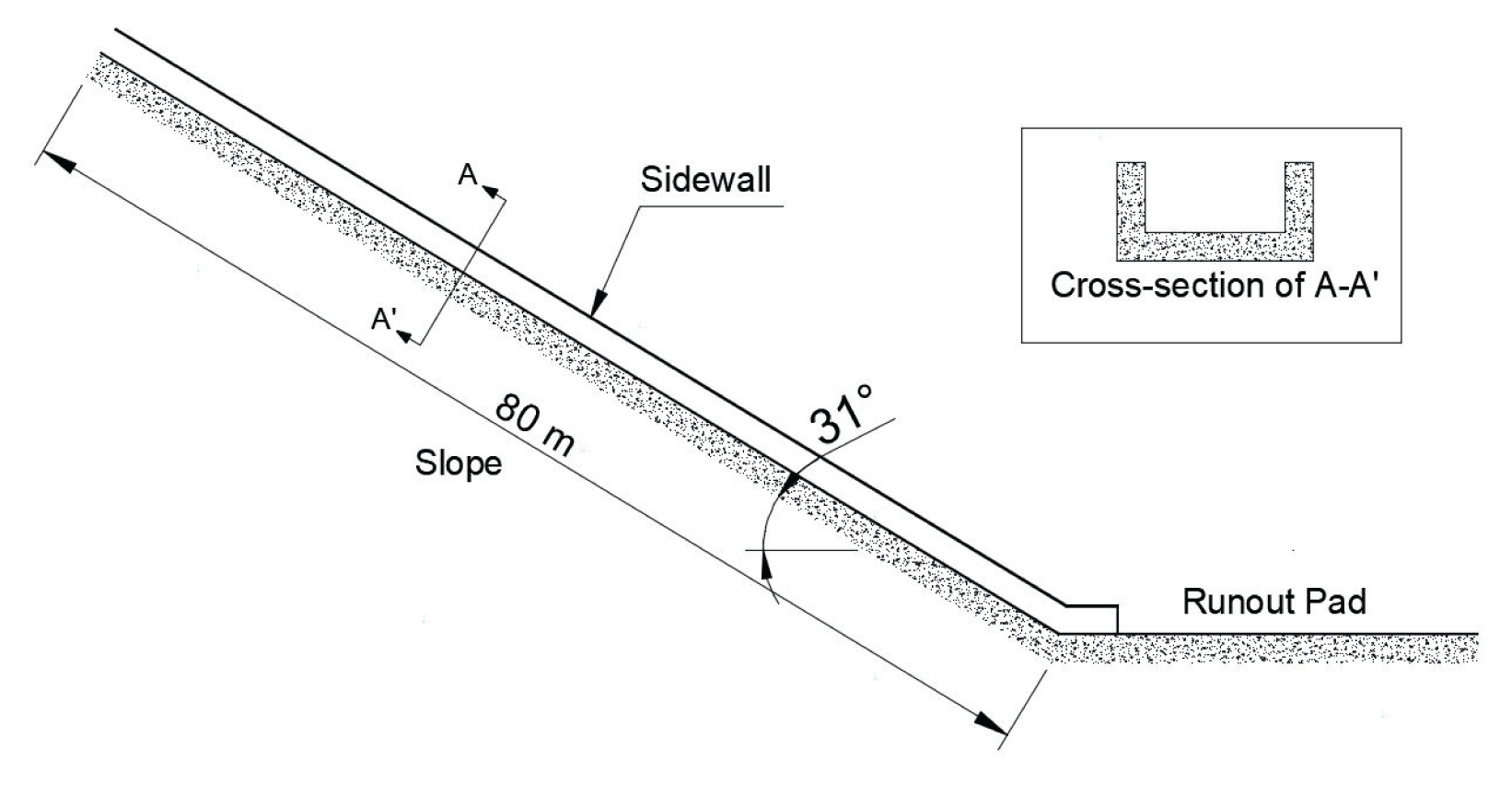
국내에서 토석류의 발생은 사면경사 20°이하에서도 발생할 수 있지만, 28~35°사이에서 가장 많이 발생한다. USGS 토석류 수로는 경사각 31°이므로, 국내 여건이 일정수준 반영되었다고 판단된다. 수로의 길이와 폭은 각각 95.0 m, 2.0 m로 기존 실험의 한계점으로 지적되었던 scale effect를 크게 완화하였다. Iverson (2015)은 차원해석과 다양한 실험결과의 비교를 통해 점성 전단 저항(viscous shear resistance)과 초과된 간극수압의 효과가 기존의 실험 규모와 실규모의 토석류 사이에 큰 차이가 있음을 보여주었다. 실험의 초기 조건은 USGS 토석류 수로에서 실험한 다른 연구자의 실험(Iverson, 1997; Iverson et al., 2011; Iverson and George, 2014)을 참고하여(12.1 m3) 적용되었다. 실험에 사용된 토석류는 모래와 실트 그리고 자갈의 혼합물로 구성되었으며, 포화도는 약 90% 정도로 결정되었다. 또한 Bulking상태의 밀도는 1820~2000 kg/m3이었으며, 마름상태의 밀도는 2520~2620 kg/m3이었다. 이러한 물성치 선택의 이유는 실제 발생하는 토석류의 재료적 특성(Iverson and LaHusen, 1993)을 재현하기 위해서였다.
실험결과 퇴적 시작부로 부터의 퇴적된 토석류의 길이는 14.7 m였고, 평균 폭은 4.0 m로 나타났다(Fig. 2(b) 참고).
2.2 UDS (Urban Debris Simulator)
UDS는 2차원 유동모델로 Jeong et al. (2017)이 개발하였으며, 기존의 토석류해석 프로그램의 한계점을 보완하였다. 다양한 형태의 격자사용이 가능하여 복잡한 구조물 및 지형 재현이 가능하며, 토석류 방향성에 대한 자유도가 크게 증가하였다(Jeong et al., 2017). UDS는 Eqs. (1)과 (2)와 같은 천수방정식을 지배방정식으로 사용하였으며, 물질의 전파보다 파의 속도가 더 크게 될 때, 해의 정확도가 다소 높은 비보존형태(Non-conservative form)를 적용하였다. 이산화 방식으로 Finite Element Method (FEM)을 선택하였으며, 급격하게 흐름 조건이 변화하는 토석류 해석에 있어서 안정적인 해를 도출하기 위해 SU/PG (Streamline-Upwind / Petrov-Galerkin method)을 도입하였다(Bova and Carey, 1966). 또한 토석류의 물질 특성을 반영할 수 있는 9가지 저항관계식들을 탑재하여, 지역적 특성에 맞는 관계식을 선택할 수 있다. Lee and Song (2017)는 Cone Spreading, 콘 주변 유동, 우면산 현장 적용에 대해 다른 연구 및 현장 data와의 비교들을 통해 UDS에 적합한 최적의 저항 모델을 찾아내고, 정확도를 확인하였으며, Jeong et al. (2018a)은 연행이 고려된 전파 특성을 USGS 토석류 수로에서 수행된 Iverson et al. (2011)의 실험결과와 비교하여 UDS의 정확성을 검증하였고, Jeong et al. (2018b)은 다양한 방재구조물에 대한 재현이 UDS로 가능함을 보여주었다.
여기서 h는 수심, ui와 uj는 수심평균된 유속이며, i가 1인 경우에는 x방향 수심평균 유속, i가 2인 경우에는 y방향 수심평균 유속이다. u는 유속백터이고, p는 압력, g는 중력가속도, n은 조도계수를 의미하며, vij는 텐서형태의 점성항으로 와점성계수(eddy viscosity)이다. H와 h는 기준선으로부터 하상까지의 거리와 수심을 나타낸다. 위식은 유도과정에서 대기압 경사항인 ∂ pa/∂ xi을 무시하였으며, 바닥전단력 항을 1차원 Saint-Vernant 방정식의 하상 마찰 경사항에 Chezy식과 Manning 계수와의 관계식(C = R1/6/n)을 적용하고, 2차원으로 확장하여, 우변의 3번째 항과 같이 표현하였다. Navier-stoke 방정식에서 시작된 UDS의 지배방정식은 정수압 가정과 Boussinesq 가정에 의해 연직방향에 대한 식은 수평방향 압력 경사항에 포함되므로(Daily and Harleman, 1966), 실질적으로 2차원 방정식이 된다. 그리고 난류경계층에 대한 Prandtl의 혼합길이 이론으로부터 다음의 관계식이 유도될 수 있다.
여기서 l은 혼합길이(mixing length)이며, U는 평균유속이다. 그러나 앞선 지배방정식 유도과정에서 도입된 가정으로 위의 식은 성립될 수 없으며, 와점성계수 vT는 가상적인 값이 된다. 본 연구에서는 다양한 흐름조건에서 복잡한 유속구조를 보다 정확하게 재현하기 위하여, 텐서형태의 와점성계수를 도입하였으며, 이를 이용하여 불규칙한 토석류의 퇴적 형상을 정확하게 재현하는 연구를 수행하였다.
3. 수치해석
3.1 시간간격 및 격자크기에 대한 민감도 분석
컴퓨터 공학의 급격한 발달로 2차원, 3차원 수치해석 모델이 활발하게 사용되고 있다. 그러나 수치모델은 이론적인 구조, 매개변수의 구성 및 입력자료 등에 의해 불확실성 요소를 내포하여, 모의 결과가 다양하게 나타날 수 있다. 특히 요소와 시간간격의 크기 선택은 모의 결과가 요소에서의 질량 및 체적 유출입을 이용하여 계산되기 때문에, 매우 중요하다. 이에 USGS 토석류 수로에서 수행한 Iverson (1997)의 실험결과를 이용하여, 본 모의 전 UDS의 격자와 시간간격에 대한 민감도 분석을 수행하였다. Iverson (1997)은 USGS 토석류 수로 특정 지점에서 선단파의 특성을 시간에 따라 측정하였으며, 본 연구에서는 선단파가 도착한 시간과 측정 지점의 거리를 이용하여 평균 유속을 측정하고, 이 값을 검증 자료로 활용하였다.
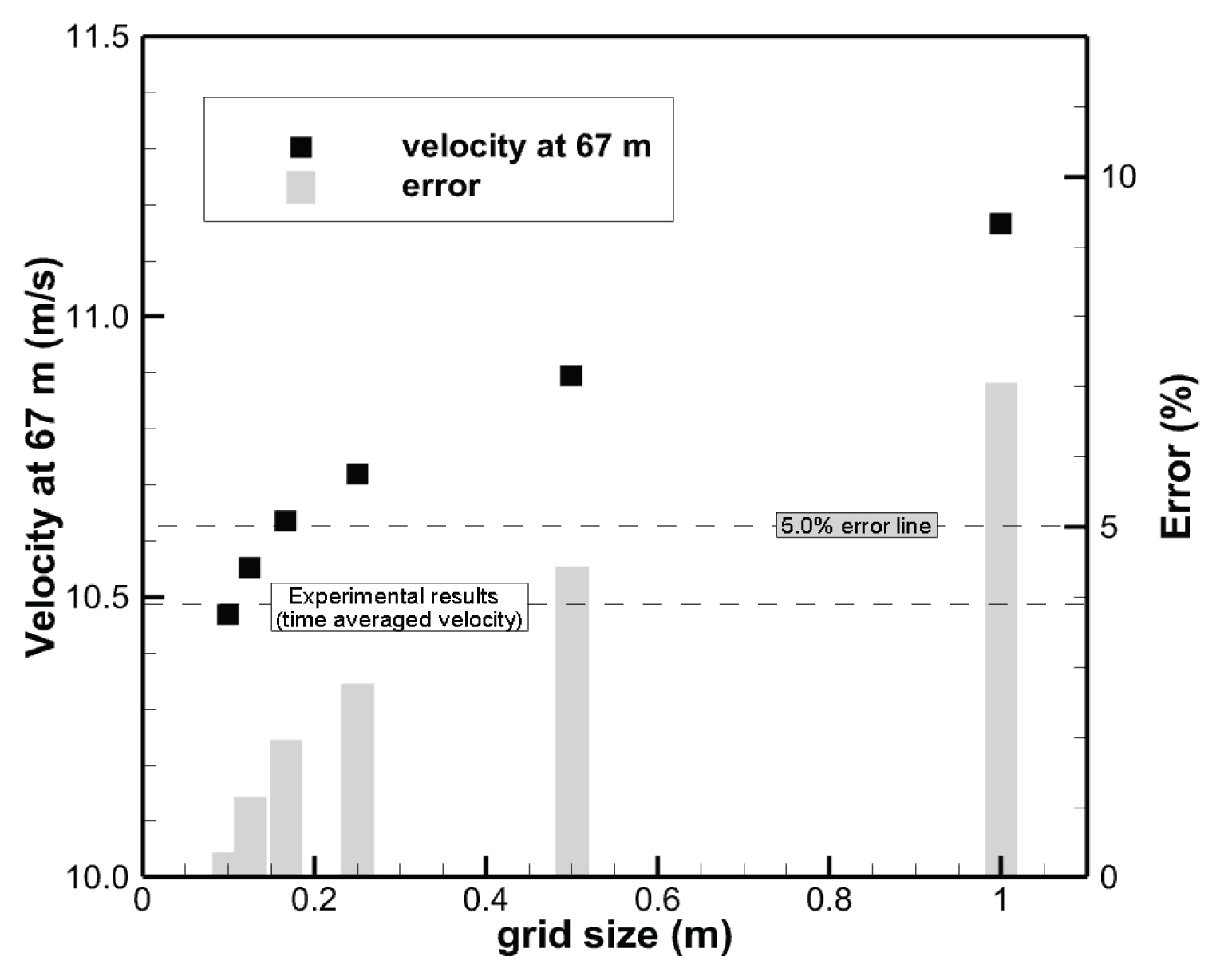
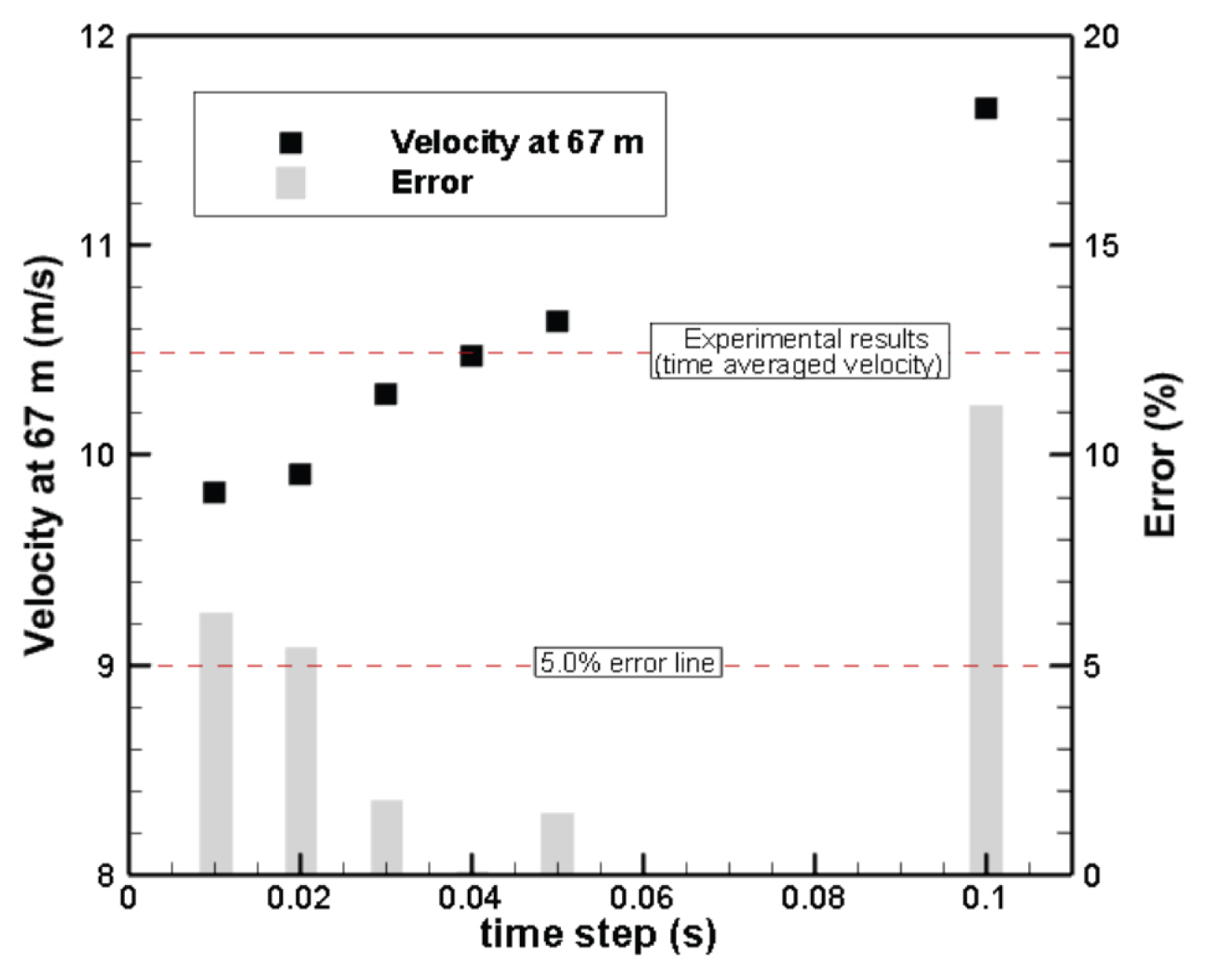
격자에 대한 민감도 분석은 USGS 토석류 수로의 폭을 고려하여 격자 크기를 0.10, 0.125, 0.167, 0.25, 0.50, 1.00 m로 결정하였다. 시간간격은 0.01~0.05 s까지 0.01 s 간격, 그리고 0.1 s의 총 6단계로 구분하였다. Iverson (1997)의 실험을 그대로 재현하고, 격자 및 시간간격에 따른 결과를 분석하였다. 토석류의 물성치는 Table 1과 같이 Iverson (1997)이 제시한 일반적인 토석류의 물성치를 사용하였으며, 이는 UDS의 입력자료로 사용되었다. Iverson (1997)은 USGS 토석류 실험수로의 67 m 지점에서 다양한 토석류의 유동특성을 분석하였는데, 본 연구에서도 67 m 지점까지의 평균유속을 분석하여 비교하였다. Fig. 3에서 보듯이 실험값과의 허용 오차 범위를 5.0%라고 가정 하였을 때, 격자 크기 1.0 m를 제외한 모든 격자에서 오차 범위 이내의 값을 보여주었다. 시간간격에서는 0.04 s에서 Iverson (1997)의 실험 결과와 가장 유사한 유동특성을 갖는 것으로 확인되었다.
앞선 분석과 동일하게 5%의 허용오차를 적용할 경우 적용가능한 시간간격은 0.03, 0.04, 0.05 s로 나타났다(Fig. 4 참조). 수치해석의 효율성을 고려하여, 0.25 m 격자와 0.04 s (오차 0.11%)의 시간간격을 수치해석의 조건으로 결정하였으며, Iverson (1997)과 동일한 USGS 토석류 수로에서 수행된 Major (1996)의 퇴적형상에 대한 실험을 재현한 수치해석에 이와 같은 최적 조건을 적용하였다. 또한 이러한 조건의 사용은 USGS 토석류 수로에서 UDS의 토석류에 대한 운동(moving) 정확도를 확보하는 의미도 있다고 판단된다.
3.2 Major의 토석류 퇴적 수치해석
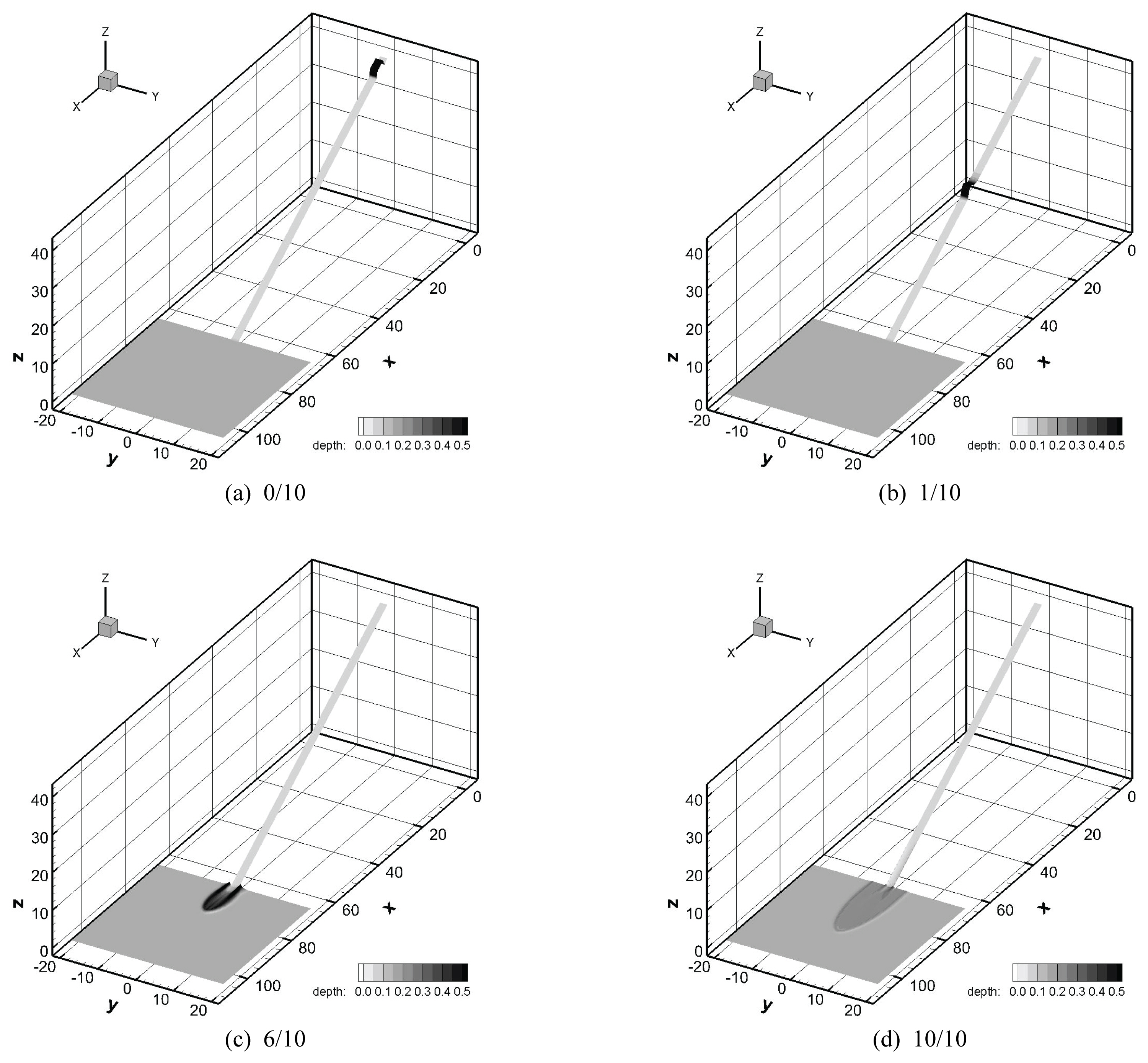
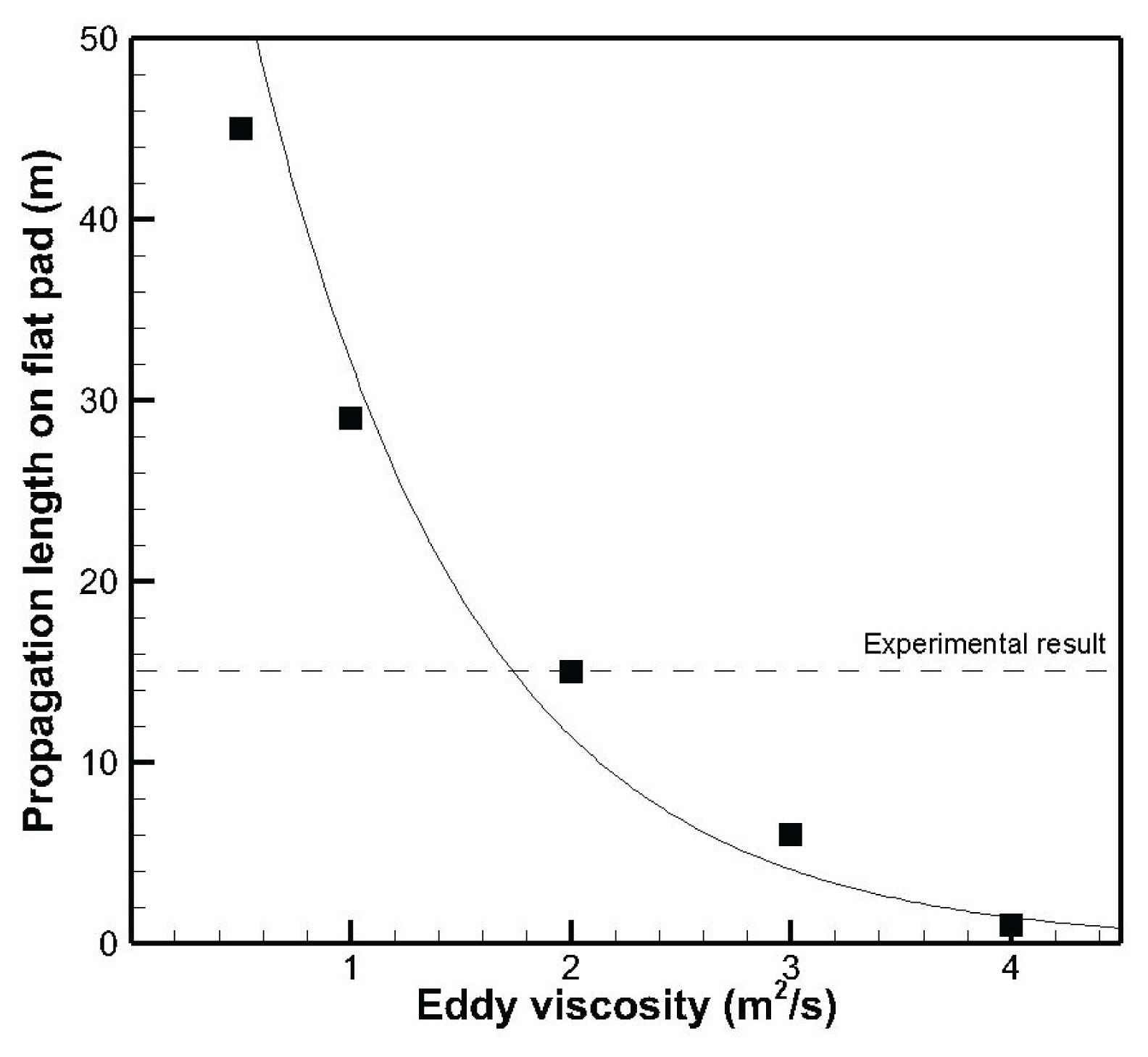
Major (1996)의 실험을 UDS를 이용하여 재현하였다. 실험에 사용된 토석류의 재료적 특성을 최대한 반영하였으며, 제시되지 않은 내부마찰각은 31°로 결정하였다. 이는 Coulomb이 본래 정의한 마찰각은 비탈면에 놓인 물체가 미끄러져 내려오기 시작하는 경사각이었는데, 결국 유동이 시작된 토석류의 경우도 비탈면의 각도와 내부마찰각이 크게 다르지 않기 때문이다. UDS는 앞서 설명한 바와 같이 텐서형태의 점성계수가 사용되며, 이를 이용하여 최적 퇴적형상에 대한 분석을 수행하였다. 우선 토석류 surge의 진행방향에 대해 와점성계수를 변화시켜가며, Major (1997)의 결과와 비교하였다. 와점성계수는 2차원 모델에서는 가상적인 값으로 수치모델의 정확도 확보를 위한 보정작업에 많이 사용된다. 수치해석은 와점성계수를 0.5, 1.0, 2.0, 3.0, 4.0과 같이 5단계로 구분하고, 이에 따른 퇴적길이를 분석하였다. Fig. 5는 UDS를 이용한 수치해석 모습이며 Fig. 6은 수치해석 결과를 정리하고 도시한 것이다.
와점성계수가 변화함에 따라 전파방향의 퇴적길이는 크게 변화하는 것으로 나타났다. Major (1997)의 실험결과와 비교할 때, 와점성계수 2.0 m2/s이 주어진 조건에서 전파방향의 토석류 퇴적 길이에 가장 적합한 값으로 확인되었다. Lee and Song (2017)은 토석류의 유동에 대한 수치모의 시 가장 안정적인 조건으로써 와점성계수 값을 0.003 m2/s로 고정하였는데, 본 연구에서 상대적으로 큰 값으로 결정된 이유는 일반적인 유동에 비하여, 토석류의 퇴적 시 더욱 큰 속도경사가 발생되며, 이는 난류점성에 의한 토석류가 가진 에너지의 더 빠른 소산을 의미한다고 해석할 수 있다. 이 때, 오차는 약 0.4%며, 길이는 14.6 m이다.
대부분의 천수방정식 기반의 토석류 유동 해석 모델들은 단일한 점성계수를 사용하기 때문에, 평평한 지형에서의 퇴적형상은 원형에 가까울 수밖에 없다. 그러나 Major (1996, 1997)의 토석류 퇴적형상에 관한 많은 실험들은 실제 토석류 퇴적 형상이 원형이 아닌, 타원에 가까운 형태임을 보여주고 있다. 이러한 타원에 가까운 형상 재현을 위하여, y방향(파의 진행방향과 수직방향)의 점성이 x방향(파의 진행방향)의 점성과 달라져야 함을 파악하였다. 이에 x방향과 y방향 점성의 비인 와점성계수비(eddy viscosity ratio, Rev)를 이용하여, 토석류의 퇴적형상을 보정하였다.
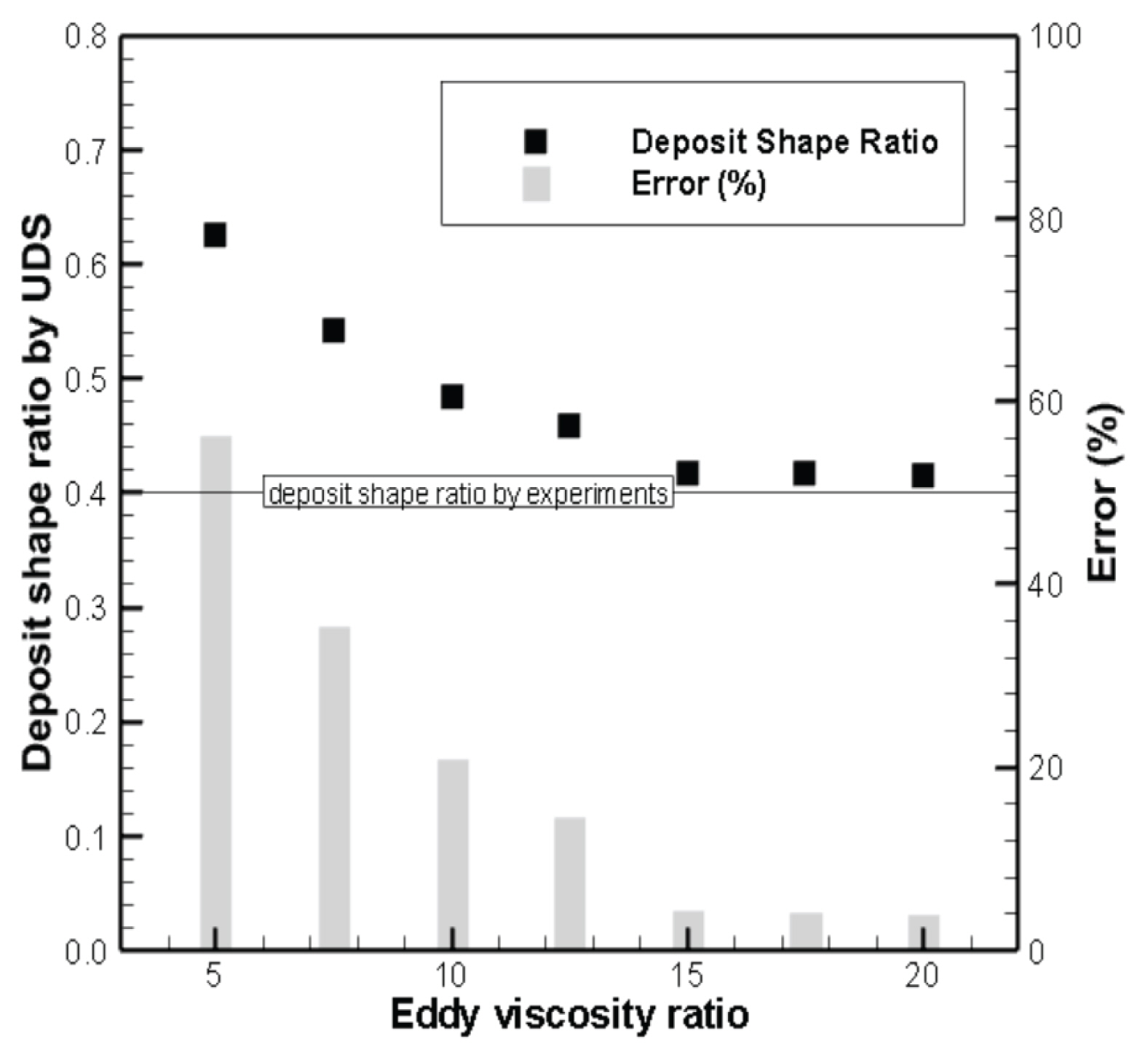
여기서 ve-xx와 ve-yy는 각각 x방향 및 y방향 와점성계수이다. 본 연구에서는 Major (1997)의 많은 실험 중 좌⋅우 대칭이 뚜렷한 case를 선정하였으며, 이 case의 실험 조건 및 재료적 특성을 UDS로 재현하였다. 이미지 분석 기술을 활용하여, Major (1997)의 전파방향 퇴적길이와 폭의 비(deposit shape ratio)를 확인한 결과 0.4였으며, 이 값을 기준으로 와점성계수비를 변화시켜가며, 수치해석을 수행하였다.
와점성계수비를 5~20까지 총 7단계로 구분하였다. 수치해석 결과, Fig. 7에서 보듯이 UDS는 와점성계수비가 15이상에서 0.41 정도로 수렴하는 경향을 보였다. 이는 토석류의 퇴적 형상을 결정하는 큰 자갈들의 흐름방향 관성(x-dir.)이 혼합으로 인한 수직방향 관성(y-dir.)에 비하여 15배 이상 크다는 것을 의미하며, 15배 이상의 차이에서는 퇴적형상의 차이가 크게 발생하지 않는 다는 것을 보여준다.
이러한 결과를 확인하기 위하여, Fig. 8과 같이 와점성계수비가 15일 경우, Major (1997)의 실험과 겹치고(overlap), 퇴적범위를 비교하였다.
UDS 수치해석 결과는 좌우가 대칭인 반면, 실제 실험은 정확한 대칭 모양으로 형성되지 않았다. 수치해석 결과가 실험 결과에 비하여 약 6.7% 큰 것으로 확인되었지만, 토석류를 모의하는 2차원 수치모델들이 퇴적과정에서 발생하는 토석류 재료 각각의 거동 메커니즘을 그대로 재현할 수 없음을 감안할 때, 이정도의 오차는 크지 않은 값이라고 판단된다.
4. 결 론
본 연구에서는 토석류의 3단계 거동 중 퇴적에 대한 형상을 2차원 수치모델을 이용하여 분석하였다. 천수방정식 기반의 UDS를 이용하여, 수치해석을 수행하였다. Major (1996, 1997)의 토석류 퇴적 형상에 대한 실험을 UDS로 정밀하게 재현하여, 실험결과와 수치해석 결과를 비교하였다. 실험에서의 퇴적형상은 단일 점성계수를 사용하였을 때, 나타날 수 있는 원형이 아니었기 때문에, UDS의 특징 중 하나인 텐서형 와점성계수를 이용하여, 불규칙한 토석류 퇴적형상을 정확하게 재현하였다. 대부분의 토석류 피해 조사 및 위험도 예측에 사용되는 주 변수가 토석류의 전파범위임을 감안할 때, 토석류의 거동 특성 중 퇴적에 대한 정확도는 매우 중요한 요소이며, 본 연구는 이러한 퇴적에 대해 와점성계수를 이용하여 정확하게 재현할 수 있음을 보여 주었다. 그러나 Major (1996, 1997)의 많은 실험은 매우 다양하고, 불규칙한 결과들을 보여주고 있지만, 본 연구는 이러한 결과들 중 비교적 대칭성이 있는 경우를 선정하여 분석하였다. 향후 비대칭적인 토석류의 형상 분석을 확률적인 접근 방법을 이용하여 분석할 것이며, 이를 수치해석에 적용하여 실제 퇴적형상을 수치해석으로 재현할 수 있도록 연구할 것이다. 또한 본 연구에서 모형의 정확도를 평가하는데 이용된 Major (1996, 1997)과 Iverson (1997)의 실험은 실험조건 및 실험에 사용된 재료 등이 다양한 형태로 변화되었기 때문에, 향후 UDS 적용시 다양한 재료적 특성을 반영하여 재현성에 대한 심도있는 연구를 수행할 것이며, 평면적인 2차원 퇴적 연구는 실제 현장 조건과 많은 면에서 동일하지 않기 때문에, 현장자료를 활용한 퇴적 재현 연구도 수행할 것이다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
Print
