 |
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 19(4); 2019 > Article |
|
Abstract
This study compared the accuracy and sensitivity of the Wet-Bulb Globe Temperature (WBGT) models developed based on domestic and international studies. The applicability of these models to formal weather observatory and user-installed sites such as the military training centers in Korea were evaluated. For the WBGT estimation, a physical model and four empirical models were used. A Liljegren model, which is known to have high accuracy, was used as the physical model. The KMA2006, JME (four-variable), KMA2016, and ABM (two-variable) models were used as the empirical models. The root-mean-square errors (RMSE) of ABM and Liljegren models obtained in this study are approximately 1 ℃ higher than RMSE results in US and New Zealand. The KMA2006 and JME models demonstrated high accuracy at RMSE of 0.45 ℃. The KMA2016 model performed better in the simulation than the physical model (RMSE of 1.06 ℃) even though only two variables were used. In particular, the KMA2016 model demonstrated good performance in the central region of the Korean peninsula, including the military training centers (RMSE of 0.75 ℃). However, it was underestimated in the southern part of the peninsula. Its performance became worse except for the time occurring maximum temperature. Therefore, at the Automated Surface Observing System stations where solar radiation and wind speed data are available, the KMA2006 and JME models can outperform other models. In the military, school, and industrial sites where only air temperature and relative humidity are observed, we expect that the WBGT can be estimated within an error range of ±0.6 ℃ using the KMA2016 model.
요지
본 연구에서는 국내외에서 개발된 습구흑구온도(WBGT) 추정모델들의 정확도와 민감도를 비교하고, WBGT 추정모델들이 한국의 기상관측지점뿐만 아니라 WBGT 활용 현장에도 적용 가능한지 평가했다. WBGT 추정에는 물리모델과 경험모델이 사용되었다. 물리모델은 선행연구에서 정확도가 높다고 알려진 Liljegren 모델을 이용하였고, 경험모델은 4가지 변수로 추정하는 한국 기상청 KMA2006과 일본 환경성 JME 모델, 2가지 변수로 추정하는 한국기상청 KMA2016과 호주기상청 ABM 모델을 적용하였다. ABM과 Liljegren 모델은 미국과 뉴질랜드에서 검증된 결과보다 RMSE가 약 1℃ 높게 모의되었다. 반면, KMA2006과 JME 모델은 RMSE가 0.45℃로 정확도가 가장 높았고, 기온과 상대습도만으로 추정하는 KMA2016 모델도 물리모델보다 모의성능이 우수했다(RMSE 1.06℃). 다만, KMA2016 모델은 최고기온이 발생하는 시간 이외에는 정확도가 감소하고, 군사훈련소를 비롯한 중부지역은 잘 모의하지만 남부지역의 WBGT는 과소 모의하는 경향을 보였다. 따라서 일사량과 풍속이 관측되는 종관기상관측장비(ASOS) 지점은 KMA2006과 JME 모델이 최적의 모의성능을 제공할 수 있고, 기온과 상대습도만 관측되는 군부대, 학교, 산업현장 등 일상현장에는 KMA2016을 활용하면 ±0.6℃ 오차범위로 WBGT를 추정할 수 있을 것으로 예상된다.
폭염은 대규모 희생자를 유발할 수 있는 자연재해 중 하나로(Kysely and Kim, 2009), 한국에서는 2018년 ‘재난 및 안전관리 기본법’에 폭염을 자연재난 항목으로 규정하여 국가차원에서 예방 및 지원 할 수 있는 법적 근거를 마련하였다. 전 세계적으로도 폭염 피해를 예방하기 위해 폭염경보시스템을 가동하고 있으며, 가장 많이 사용되는 폭염진단지수는 일 최고기온이다(McGregor et al., 2015; Lee et al., 2016). 하지만 기온은 인체에 직접 닿는 태양 복사열과 인체 발한기작 효과에 관련된 대기 습도를 고려하지 못하는 한계가 있다. 따라서 국제표준화기구(ISO)는 두 영향을 모두 반영한 습구흑구온도(Wet Bulb Globe Temperature, WBGT)를 열 스트레스 지표로 채택하여, 산업 및 군사, 스포츠, 상업 분야에서 고온 환경의 활동규제 기준으로 제안하고 있다(ISO 7243, 1989). 여기서 WBGT는 습구온도와 흑구온도, 기온으로 산출되는 폭염지수로, 미군 훈련 시 군인들의 온열질환 피해를 줄이기 위해 개발되었으며(Yaglou and Minard, 1957), 현재는 미국연방 직업안전보건국(OSHA), 미국 및 국내 군사훈련소, 일본, 호주, 홍콩 기상청 등 에서 이용하고 있다. 또한 한국 기상청에서도 더위체감지수라는 명칭으로 2018년부터 WBGT 추정 값을 제공하고 있다. 그러나 WBGT를 산출하기 위해서 정규관측요소가 아닌 흑구온도가 필요하기 때문에 Yaglou and Minard (1957)의 원형모델을 이용한 예측 및 고해상도 기후분석이 어렵다는 단점이 있다. 이를 해결하기 위해, 각국의 기상 및 환경 당국에서는 정규관측요소로 WBGT를 추정할 수 있는 물리모델과 경험모델들을 개발하고 있다.
WBGT 물리모델은 대기와 흑구 및 습구 온도계 간의 역학적 열 교환을 모의한 것으로, Liljegren et al. (2008)과 Gaspar and Quintela (2009) 등이 개발한 모델들이 있다. 이 중 Liljegren 모델은 미국 내 다양한 기후에서 검증한 결과, 오차가 1℃ 이내로 정교하다(Liljegren et al., 2008). 또한, 미국 군부대(Patel et al., 2013)와 뉴질랜드(Lemke and Kjellstrom, 2012)에서 여러 추정모델들을 비교한 결과, Liljegren 모델의 최대 평균제곱근오차(RMSE)가 각각 1.71℃, 0.95℃로 가장 우수한 모의성능을 보였다. 다만, 물리모델은 연산이 복잡하여 일반인들이 사용하기에 불편하다는 단점이 있다.
경험모델은 WBGT와 기상청 관측요소들을 회귀분석하여 얻은 모형으로, 한국 기상청(Korea Meteorological Administration, KMA)에서 개발한 KMA2006, KMA2016 모델(KMA, 2006, 2016)과 Ono and Tonouchi (2014)가 개발하고 일본 환경성(Japanese Ministry of the Environment, JME)에서 사용하는 JME 모델(JME, 2006), 미국 스포츠의학 대학에서 제안하고(ACSM, 1984) 호주 기상청(Australian Bureau of Meteorology, ABM)에서 사용하는 ABM 모델(ABM, 2010) 등이 있다. 경험모델은 활용이 용이하다는 장점이 있으나, 다른 기후대에 도입 시 재검증이 필요하다는 단점이 있다.
현재 한국에서 WBGT 추정모델을 이용한 폭염지수들의 온열질환피해 감지율 비교와 도시의 열 쾌적도 평가, 기후변화에 따른 생산력 변화에 대한 연구들이 진행되고 있지만(Lee et al., 2016; Park et al., 2016; Lee et al., 2018), WBGT 추정모델들을 관측자료와 비교하여 정확도를 검증한 연구는 거의 없다. 따라서 본 연구에서는 한국(KMA2006, KMA2016)과 일본(JME), 호주(ABM), 미국(Liljegren)에서 개발 및 활용하고 있는 WBGT 추정모델에 한국 기상자료를 적용하여 WBGT 관측값과 비교하고 정확도를 분석했다. 또한 정규관측소뿐만 아니라 WBGT 활용현장(군사훈련소 등)에 대한 추정모델의 적용 가능성을 평가하였다.
Yaglou and Minard (1957)가 제안한 WBGT 모델 원형은 습구온도(Tw, ℃)와 흑구온도(Tg, ℃), 기온(Ta, ℃)의 가중평균함수이며(Eq. (1)), 본 연구에서 분석된 WBGT 추정모델들은 기상요소의 적용 개수에 따라 다음과 같이 나눠진다. 5개 변수(기온, 상대습도, 일사량, 풍속, 기압)를 이용하는 Liljegren 모델(2.1), 4개 변수(기온, 상대습도, 일사량, 풍속)를 이용하는 KMA2006과 JME 모델(2.2), 2개 변수(기온, 상대습도)를 이용하는 KMA2016, ABM 모델(2.3)이 있으며, 총 5개 추정모델들을 평가했다.
Liljegren 모델은 기온과 상대습도, 일사량, 풍속, 기압으로 습구온도와 흑구온도를 추정하여 Eq. (1)에 대입한 모델이다(Liljegren et al., 2008). 여기서 습구온도는 젖은 심지에서 발생하는 에너지평형 원리를 기반으로 정의된다(Eq. (2)).
△H는 기화열, Cp는 정압비열, M H 2 O
흑구온도는 주변 공기의 열복사 교환(1항), 대류에너지 교환(2항), 흑구로 전달되는 태양복사에너지(3항)의 합으로 정의된다(Eq. (3)).
여기서 εa는 열 복사에 대한 공기의 방사율, εg는 흑구의 방사율, σ는 스테판-볼츠만 상수, S는 전천일사(Wm-2), αg는 지면 반사도, θ는 태양고도각(˚), fdir은 S에 대한 직달일사량비율, αsfc는 표면 반사도이다. 습구온도와 흑구온도 방정식을 풀기 위해선 복잡한 반복수치해법이 사용되어 WBGT 추정이 간단하지 않다. 따라서 Liljegren은 WBGT 연산소프트웨어를 제공하고 있다. 본 연구에서는 Fortran 언어기반의 Argonne National Laboratory WBGT_ver1.1 프로그램(Liljegren, 2008)을 이용하였다.
KMA2006 모델은 한국 기상청 서울(#108) 종관기상관측장비(ASOS) 지점에서 2006년 9월 26일부터 2007년 1월 31일까지 관측한 흑구온도와 기온, 상대습도(RH, %), 풍속(WS, m s-1), 시간누적일사량(Slr, MJ m-2 h-1)의 선형회귀분석으로 흑구온도 추정모델(TgKMA2006, Eq. (4))을 개발하여, Eq. (1)에 적용한 것이다. 여기서 TgKMA2006는 관측 값에 대해 95.1% 설명력을 가진다. 다만, 흑구의 직경이 표준규격보다 작은 50 mm의 소형 흑구(WBGT-101, Kyoto Electronics Manufacturing Co., Ltd.)를 사용하여, 태양고도가 높아질수록 표준규격의 흑구보다 온도가 더 낮아지는 경향이 있다(KMA, 2006).
습구온도는 Stull (2011)이 개발한 기온과 상대습도의 경험식으로 추정하였으며(Eq. (5)), 상대습도 5~99%, 기온 -20~50℃에서 유효하고, 평균절대오차 0.3℃ 미만의 모의성능을 가졌다.
JME 모델은 일본 나고야 관측소에서 1년 동안(2008년) 관측된 표준규격의 흑구온도 관측값을 분석하여 개발되었다(Eq. (6)).
여기서 SR은 kWm-2 단위의 전천일사이다. 일본에서 JME 모델을 검증한 결과(Ono and Tonouchi, 2014), 평균오차(Mean bias, MB)는 2007년과 2009년에 대해 각각 0.017℃, 0.019℃, 5개 도시에 대한 MB 변화는 –0.109 ~ 0.004℃로 지역별 큰 차이가 없었다. 일본 환경성에서는 JME 모델로 산출된 829지점 WBGT 추정 값과 11개 지점 실측 값, 수치모델을 결합한 3일 예측 값을 폭염감시기간 동안 제공하고 있다(JME, 2006).
한국 기상청의 ASOS 96개소 중 일사량 관측지는 47개소에 불과하기 때문에(2018년 12월 기준), 4 변수 모델을 전국으로 확대 적용하기에는 한계가 있다. 따라서 통계적으로 유의한 성능을 가지며 일사량 자료 없이 WBGT를 추정할 수 있는 모델이 요구되었고, 기상청은 기온과 상대습도를 이용한 KMA2016 모델을 개발하였다(KMA, 2016; Eq. (7)). 회귀분석에는 2016년 서울(#108) ASOS와 서귀포 국립기상과학원(#884, 이하 NIMS) 자동기상관측장비(AWS) 지점에서 관측된 WBGT가 사용되었다. 습구온도는 Stull (2011)의 추정식(Eq. (5))을 적용했다. KMA2016 모델은 2016년에 관측된 WBGT에 대해 97.5%의 설명력을 가졌고, 같은 기간 전국 5개 도시(청주, 대구, 전주, 부산, 거제)에 적용했을 때에도 적합도가 높았다(R2 = 0.9659).
호주기상청에서 사용되는 ABM 모델은 기온과 수증기압(e, hPa)으로 추정된다(Eq. (8)). 여기서 수증기압은 기온과 상대습도만으로 유도할 수 있기 때문에(Eq. (9)) 운동장 및 공장의 WBGT 산출이 용이하여, 일상 현장에서 실용적으로 사용되고 있다(Altinsoy and Yildirim, 2015; Cooper et al., 2016; Kakamu et al., 2017; Smith et al., 2017). 다만, 정오에 풍속이 약한 날을 대상으로 개발되어, 이 조건을 만족하지 못 할 때는 과대평가 될 수 있다. 이를 정량적으로 분석하기 위해 Grundstein and Cooper (2018)는 Liljegren 모델 결과를 참값으로 가정하고 미국 조지아 주의 19개 지점에 대해 6년간(2008-2014년) 8~9월에 구동된 ABM 모델결과와 비교했을 때, 전반적으로 ABM모델이 과대 모의하고 하루 중 정오의 오차가 1.2~1.6℃로 가장 작다는 결과를 얻었다. 하지만 정오에도 바람이 약하면(<-2σ) 3℃이상 과소모의하고, 운량이 많을 때는(>1.8σ) 3℃이상 과대 모의하는 경향을 가졌다.
중부지역에서 내륙성 기후인 서울 ASOS와 남부지역에서 해양성 기후인 서귀포 NIMS AWS 지점에 흑구온도계(Table 1)를 ISO 7243 규격에 따라 설치하여 WBGT를 관측하였다. 기온과 상대습도, 풍속, 일사량은 ASOS 관측자료를 이용하였으며, NIMS에는 일사계를 추가 설치했다(Figs. 1(a) and 1(b)). 서울과 NIMS의 관측자료는 KMA2016 모델 개발에 사용되었다. 따라서 다른 지점에 대한 적용가능성도 평가하기 위해, 국내에서 WBGT를 사용하고 있는 군사훈련소(논산, 이천, 화천)와 그 지역 AWS 지점에서 WBGT 모의 성능을 추가 검증하였다. 훈련소에서도 알콜온도계를 이용한 흑구온도가 관측되고 있지만, 필요시에만 기록하기 때문에 연속적인 정시관측 값을 알 수 없다. 따라서 본 연구에서는 1시간 간격의 흑구온도 자료를 얻고자 별도의 자동관측장비를 설치했다(Fig. 1c-h). 또한 훈련소에는 일사계와 자연통풍식 온습도계도 설치하였다.
분석기간은 지점마다 차이가 있으며, 서울과 NIMS는 2016년 4월부터 2018년 12월까지, 논산과 이천, 화천(군사훈련소⋅AWS)은 2018년 여름(6-9월)이다.
WBGT 경험적 추정모델들은 대부분 계절구분 없이 회귀분석을 통해 개발되었다. 따라서 WBGT 관측 전 기간에 대한 상관계수(r)와 평균오차(MB), 평균제곱근오차(RMSE)를 비교한 결과(Table 2(a)), 모든 모델들이 통계적으로 유의한 적합도를 보였다(r=0.98~0.99). 이 중 4 변수 모델 KMA2006과 JME의 상관계수가 가장 높았고(r=0.99), RMSE도 0.47~0.48℃로 가장 낮게 분석되었다. 일사량과 풍속이 고려되지 않은 2 변수 모델 중 ABM은 관측 값에 비해 크게 과대모의(MB 4.6℃)하였고, 5개 모델 중 가장 낮은 정확도를 보였다. 하지만 KMA2016 모델은 4 변수 모델과 유사한 오차범위를 가졌고, 물리모델 Liljegren보다 RMSE가 낮았다.
폭염경보시스템에 주로 사용되는 여름철 1500 LST에 대한 정확도 분석결과에서도(Table 2(b)), WBGT 관측 값과 4 변수 모델들(KMA2006, JME) 추정 값의 상관도와 오차는 전 기간에 대한 분석결과와 거의 동일했고, 2 변수 모델들과 물리모델의 지점평균 상관계수는 0.9424까지 감소했다. 관측지점별로 비교하면, ABM과 Liljegren 모델은 관측지역과 관계없이 상관도가 낮아지고, KMA2016 모델은 NIMS 지점의 상관계수가 서울지점에 비해 크게 감소하는 경향을 보였다. 또한 분석기간을 여름철 1500 LST로 제한하면서 대부분의 RMSE가 낮아지는데, Liljegren 모델의 두 지점과 KMA2016 모델의 NIMS 지점만 RMSE가 0.4~0.5℃ 증가하여 정확도가 감소했다. Fig. 2에서도 KMA2016 모델이 NIMS 지점에서 과소 모의하는 경향이 뚜렷하게 보이고, 반대로 ABM 모델과 Liljegren 모델은 모든 지점에서 과대 모의하는 특징이 나타났다.
다양한 기법으로 개발된 WBGT 추정모델들은 시간 별 정확도가 다를 수 있다. 이를 확인하기 위해, 서울 ASOS에서 3년간 관측된 여름철 WBGT의 시간 별 MB를 분석했다(Fig. 3). ABM 모델은 Grundstein and Cooper (2018)의 연구결과와 같이, MB는 정오에 가장 작았으나 규모가 미국보다 컸고(2.3℃), 일몰 후에는 최대 5.1℃까지 증가했다. 이에 반하여 Liljegren 모델은 정오에 최대 오차가 발생했고, 일사가 없을 때에는 MB가 ±0.15℃ 미만의 정확도를 보였다. 이 두 모델에 비해 한국과 일본의 경험모델들은 주간 오차 범위가 ±1℃ 였고, 4 변수 모델들은 주야 관계없이 MB가 ±0.5℃ 이내로 정확했다. KMA2016 모델은 야간 MB가 1.58℃까지 증가하나 15시에 최저로 감소하여(MB -0.09℃), 일 중 최저 MB는 4 변수 모델들과 유사했다.
WBGT 산정 시 기상변수에 따른 민감도를 정량적으로 분석하기 위해, 표준환경 조건에서 조절변수의 증가에 따른 WBGT 변화량을 비교했다. 여기서 표준환경은 서울관측소 여름 1500 LST 기상요소의 중앙값(50%ile)으로 정의하였다(Table 3). 변수 별 WBGT 민감도(Sensitivityvar)는 표준환경(varmode)에서 폭염이 되는 90%ile (varheat)로 변할 때 WBGT의 변화율을 산출하고, 변동범위가 다른 변수간의 표준화된 변화량을 비교하기 위해, 조절변수의 0.25σ (var0.25σ) 증가에 따른 WBGT 변화량으로 정의했다(Eq. (10)). 여기서 0.25는 편의상 기온 1℃에 해당하는 표준편차 비율로 정의된 것이다. 또한, 상대습도와 풍속은 폭염환경과 음의 상관이므로, 50%ile에서 10%ile로 변하는 비율로 산출하였다.
표준환경에서 기상요소 별 민감도는 Table 4와 같다. 흑구온도 관측 값(OBS)으로 산출되는 WBGT는 기온이 0.96℃ (0.25σ) 상승할 때 0.94℃증가하며, 영향력이 가장 큰 요소로 분석되었다.
그 다음은 상대습도로, 기온과 같은 비중인 0.25σ, 즉 4.35% 상승할 때 WBGT는 0.57℃ 증가하였다. WBGT 추정모델들도 기온변화에 따른 WBGT 변화가 0.81 ~ 1.03℃로 가장 크게 나타났고, 나머지 변수들은 상대습도, 일사량, 풍속, 기압 순의 영향력을 보였다. 이 중 기압의 기여도는 거의 없었고, 풍속에 따른 WBGT 변화도 -0.23 ~ -0.01℃로 매우 약하게 나타났다. 모델 별로 비교했을 때, 2 변수 모델들은 일사의 영향이 제거되면서 기온변화에 더 민감하게 반응하고, KMA2016 모델은 상대습도 비중이 감소되었다. Fig. 2에서 다른 모델에 비해 과대 모의되는 경향을 보인 ABM 모델은(MB 2.78℃) 기온과 상대습도 모두 민감하게 반응하였다. 또한, 기온 증가에 따른 WBGT 변화를 묘사한 Fig. 4에서, ABM은 습도가 49%, 기온이 30℃ 이상인 환경에서 WBGT가 비선형적으로 증가하는 특징을 보였다. 또한 Liljegren 모델을 제외한 나머지 모델들은 풍속이 10%ile, 50%ile, 90%ile일 때, WBGT 변화가 거의 없는 것을 확인 할 수 있다.
WBGT 추정모델들을 전국으로 확대 적용할 경우에도 모의 성능이 유지되는지 확인하기 위해, 정규 관측소가 아닌 WBGT 활용현장의 관측자료에 대해 추가 검증을 수행했다. 본 연구에서는 논산과 이천, 화천에 위치한 군사훈련소를 비교 관측지로 선정하였고, Liljegren 모델은 영향반경 내 유효한 기압자료가 없기 때문에 본 검증에서 제외하였다.
2018년 여름 동안 (a)정규관측소(서울, NIMS)와 (b)군사훈련소(논산, 이천, 화천)의 WBGT 추정모델 정확도를 비교한 결과(Tables 5(a) and (b)), KMA2006 모델의 훈련소 평균 RMSE는 0.87℃로 정규관측소의 평균 RMSE보다 0.37℃ 높았다. 또한 JME 모델의 RMSE도 정규관측소에 비해 0.31℃ 높았다. 반면 KMA2016 모델은 정규관측소보다 훈련소의 모의 정확도가 더 높았다. 이는 NIMS의 RMSE가 1.51℃까지 증가했기 때문이며, 서울에서 모의성능은 훈련소와 비슷한 수준이었다(0.72℃). 또한, 훈련소에서 정확도는 KMA2016 모델이 비교 모델 중 가장 우수했다.
정규관측소 외에는 대부분 자연통풍 차광통 속에서 건구온도가 관측된다. 이는 ISO 7243의 WBGT 관측규정과는 일치하나, 차광통의 복사 흡수열과 기류정체 때문에 기온이 실제보다 높게 측정될 수 있다. 따라서 한국과 일본기상청의 정규관측소(ASOS, AWS)에서는 차광통 내 4~6 ms-1의 강제순환장치를 설치하도록 기상관측지침으로 규정하고 있다(JMA, 2012; KMA, 2018). 또한 Ono and Tonouchi (2014)는 자연통풍 환경에서 관측된 WBGT는 강제통풍 조건에 비해 0.5℃ 높아 질 수 있다고 밝힌 바 있다. 따라서 통풍조건이 추정모델의 정확도에 미치는 영향을 확인하기 위해, 2018년 8월 자연통풍 환경에서 관측된 논산, 이천, 화천 군사훈련소 WBGT와 강제통풍 환경에서 관측된 AWS의 WBGT를 비교하였다(Tables 5(b) and (c)). 그 결과, KMA2006과 JME 모델의 RMSE는 두 조건에 따른 차이가 거의 없었지만, KMA2016과 ABM 모델은 자연통풍 환경에서 RMSE가 강제통풍 환경에 비해 각각 0.22℃, 0.68℃ 더 높게 나타났다. 즉, 2 변수 추정모델은 4 변수 추정모델보다 기온에 따른 WBGT 민감도가 크기 때문에, 차광통 내 통풍방식에도 영향을 받는 것으로 분석된다.
본 연구에서는 2016년부터 2018년까지 여름 동안(6월-9월) 서울과 NIMS에서 관측된 WBGT를 바탕으로, 한국과 일본, 미국에서 개발된 WBGT 추정모델들의 정확도를 검증하고, 각 모델의 입력자료 별 WBGT 민감도를 분석하였다. 또한 정규관측소와 더불어 WBGT 활용현장(군사훈련소 등)에 대한 확대 적용가능성을 평가하였다.
ABM 모델은 미국 조지아 주의 연구결과(Grundstein and Cooper, 2018)와 같이 한국에서도 시간별 MB가 정오에 최소가 되었다가 점차 증가되는 일 변동성을 가지며, 미국보다 MB가 약 1℃ 더 높은 경향이 있었다. 선행연구와 공통적으로 나타나는 야간 MB 증가현상은 ABM 모델이 WBGT 원형모델의 습구온도와 일 변동성이 반대인 습도변수를 적용하여, 정오 WBGT에 최적화 한 것이 원인으로 보인다. 2016년부터 2018년까지 여름동안(JJAS) 서울관측소에서 습구온도(Tw)의 일 변동은 건구온도와 같이 1500 LST에 최고치를 가지는 반면, ABM 모델의 수증기압(e)은 같은 시각에 최저치가 발생한다(Fig. 5). 따라서 정오에 최적화된 ABM 모델은 시간이 지날수록 MB가 급증하게 된다. 또한 ABM 모델이 한국에서 과대모의 되는 것은 상대습도가 49%(한국기후의 50%ile)이상이고 기온이 30℃이상인 환경에서 WBGT의 변동성이 커지는데, 미국 조지아 주보다 한국의 여름이 더 고온다습하기 때문에 WBGT가 높게 모의된 것으로 분석된다(Fig. 4).
따라서 ABM 모델을 적용하기 위해서는 현지의 WBGT 관측을 통한 보정계수 분석이 필요하다. 또한 정오에 최적화 되어있기 때문에 시간별 폭염정보나 열대야와 같은 야간 폭염특성 분석에는 적합하지 않은 것으로 판단된다.
Liljegren 모델은 미국 조지아 주(Patel et al., 2013)와 뉴질랜드(Lemke and Kjellstrom, 2012)에서 검증된 결과보다 RMSE가 약 0.3℃, 1.0℃ 높게 나타났다(한국 1.96℃). 이는 분석기간과 시간, 지표면 알베도 설정 차이에 따른 결과로 분석된다. Liljegren 모델은 습구온도에 비해 흑구온도의 오차범위가 커서 일출 후에 MB가 최대 2.3℃까지 증가하고 야간에는 0.15℃ 미만으로 낮아지는 특징이 있다(Fig. 3). 이로 인해 지역별 모의 성능과 관계없이 분석기간과 시간에 따라 RMSE 차이가 크게 나타날 수 있다. Patel et al. (2013)은 2007년 여름 주간의 WBGT 추정 값을 평가하여 한국의 RMSE와 유사한 반면, 짧은 기간(4일)의 24시간 WBGT 추정값으로 평가된 뉴질랜드의 RMSE는 한국보다 약 1℃ 낮았다. 하지만 뉴질랜드에서도 1100 LST~1200 LST의 MB는 2℃이상 증가된다고 분석되었기 때문에, 모델 분석기간과 시간대를 일치시키면 선행연구와 정확도가 유사할 것으로 예상된다. 또한 본 연구에서는 지표 알베도를 Liljegren 모델 기본 설정 값(0.45)으로 모의했는데, 잔디 상의 지표 알베도는 0.2 (Betts and Ball, 1997)로 실제보다 반사도가 높게 정의되었다. 이로 인해 나지에서 관측된 선행연구의 WBGT보다 RMSE가 높게 분석된 것으로 사료된다. 따라서 지표 알베도를 0.2로 수정하여 서울지점 1500 LST WBGT를 재평가한 결과, RMSE는 1.12로 향상되었고, Liljegren 모델은 위 세 가지 조건만 유의하면 다양한 기후지역에 적용하더라도 모의성능의 편차가 적을 것으로 판단된다.
일사량과 풍속을 포함한 4 변수 추정모델인 KMA2006과 JME모델은 RMSE가 0.45℃로 정확도가 가장 높았고, 그 다음으론 2 변수 추정모델 KMA2016가 모의성능이 우수했다(RMSE 1.06℃). 특히 KMA2016 모델은 선행연구에서 정확도가 높다고 알려진 물리모델 Liljegren보다 모의성능이 우수했고, 군사 훈련소에 적용했을 때 비교모델 중 가장 적은 오차를 보여줬다(RMSE 0.75℃).
종합적으로 5가지 모델을 평가했을 때, 일사량과 풍속이 관측되는 ASOS 지점들의 WBGT는 KMA2006과 JME 모델이 최적의 성능을 보였고, 기온과 상대습도만 관측되는 군부대, 학교, 공장 등에서는 KMA2016 모델을 활용하면 ±0.6℃ 오차범위로 정확도가 높은 WBGT 정보를 얻을 수 있다. 다만, KMA2016 모델은 1500 LST 외에는 시간 별 MB가 ±1.6℃까지 증가하고, 남부지역의 WBGT는 과소 모의하는 경향을 보인다. 또한 자연통풍 차광통을 이용할 경우 RMSE가 0.22℃ 더 증가할 수 있다. 따라서 이 모델을 적용할 경우, 관측조건에 따른 오차를 감안하고, 시간 별 폭염정보 보다는 일 최고값을 제공하는 것이 타당할 것으로 판단된다. 더불어 남부지역에 대한 WBGT 정확도 개선 연구가 추후 수행된다면, 산출이 용이하면서 모의성능이 우수한 모델이 될 것으로 사료된다. 본 연구에서는 WBGT 관측 값을 통한 실황 값을 평가하였으며, WBGT 예측 정확도는 수치예보모델의 기상요소 별 예측오차에 따라 달라질 수 있다. 또한, 입력변수가 많은 KMA2006과 JME 모델이 KMA2016 모델보다 예측성능이 낮아 질 가능성도 배제할 수 없다. 따라서 현업 수치예보모델에 따른 예측시간 및 해상도 별 예측정확도에 관한 연구도 향후 이뤄져야 할 것이다.
감사의 글
본 연구는 기상청/국립기상과학원 연구개발사업 "기상업무 지원기술개발연구-생명산업기상기술개발(KMA2018-00621)"의 일환으로 수행되었습니다. 이 연구의 Liljegren 모델은 미국에너지부(Contract No. DE-AC02-06CH11357) 산하 UChicago Argonne, LLC가 개발한 Argonne WBGT model_v1.1 프로그램을 제공받아 사용되었으며, 더불어 WBGT 관측 및 운영에 도움을 주신 분들께 감사를 드립니다.
Fig. 1
Automatic Observation Instruments of Globe Bulb Temperature Installed in (a) Seoul ASOS station and (b) NIMS AWS station, (c) Nonsan, (d) Icheon and (e) Hwacheon army training center (T.C.), (f) Nonsan, (g) Icheon and (h) Sangseo (in Hwacheon) AWS station

Fig. 2
The Relationship Between Observations and Estimations of WBGT in (a) Seoul and (b) NIMS Stations at 15KST Summer (JJAS) from 2016 to 2018
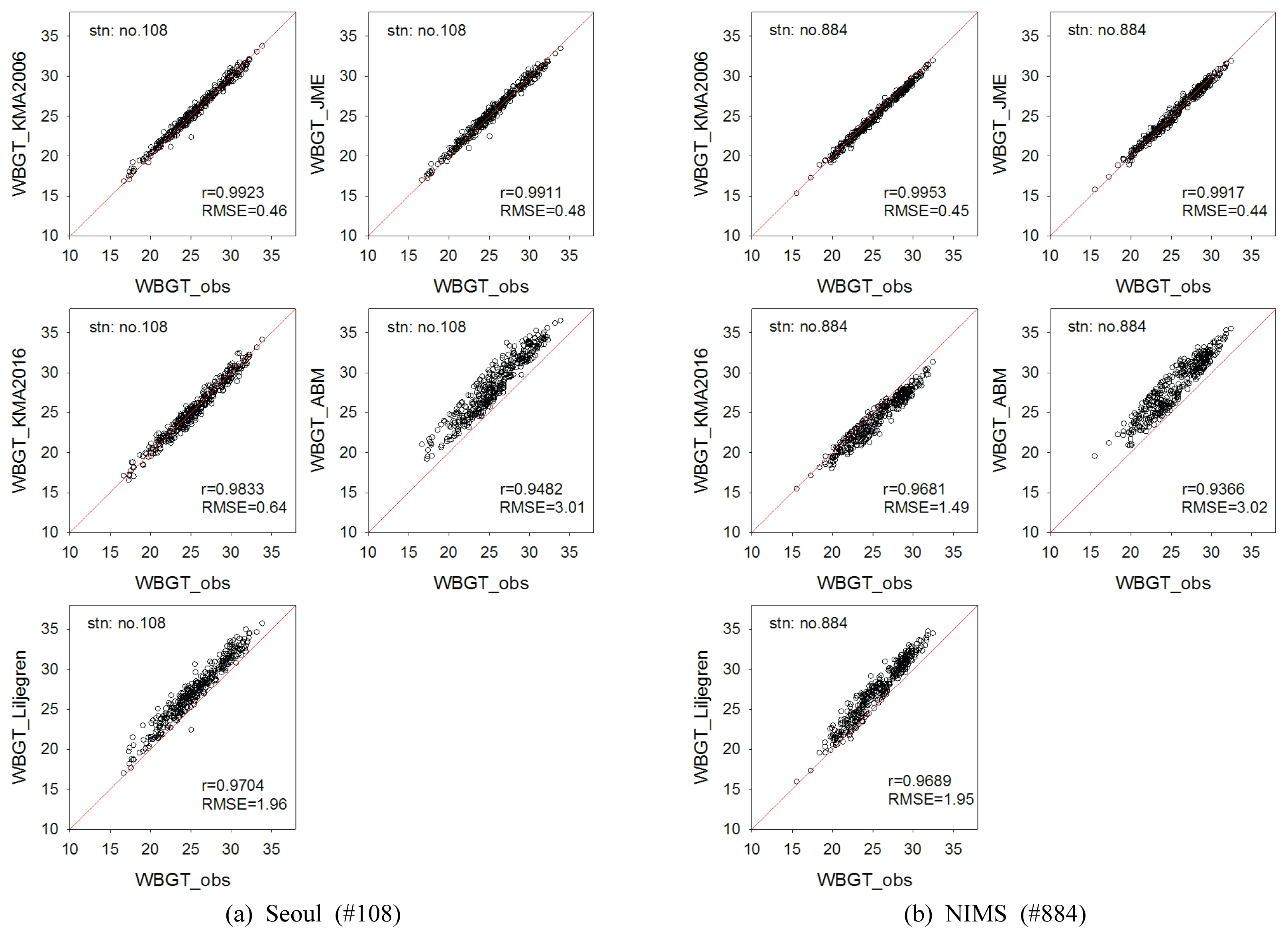
Fig. 3
Hourly Mean Bias (MB) Between Observations and Estimations of WBGT in Seoul Station During Summer (JJAS) from 2016 to 2018
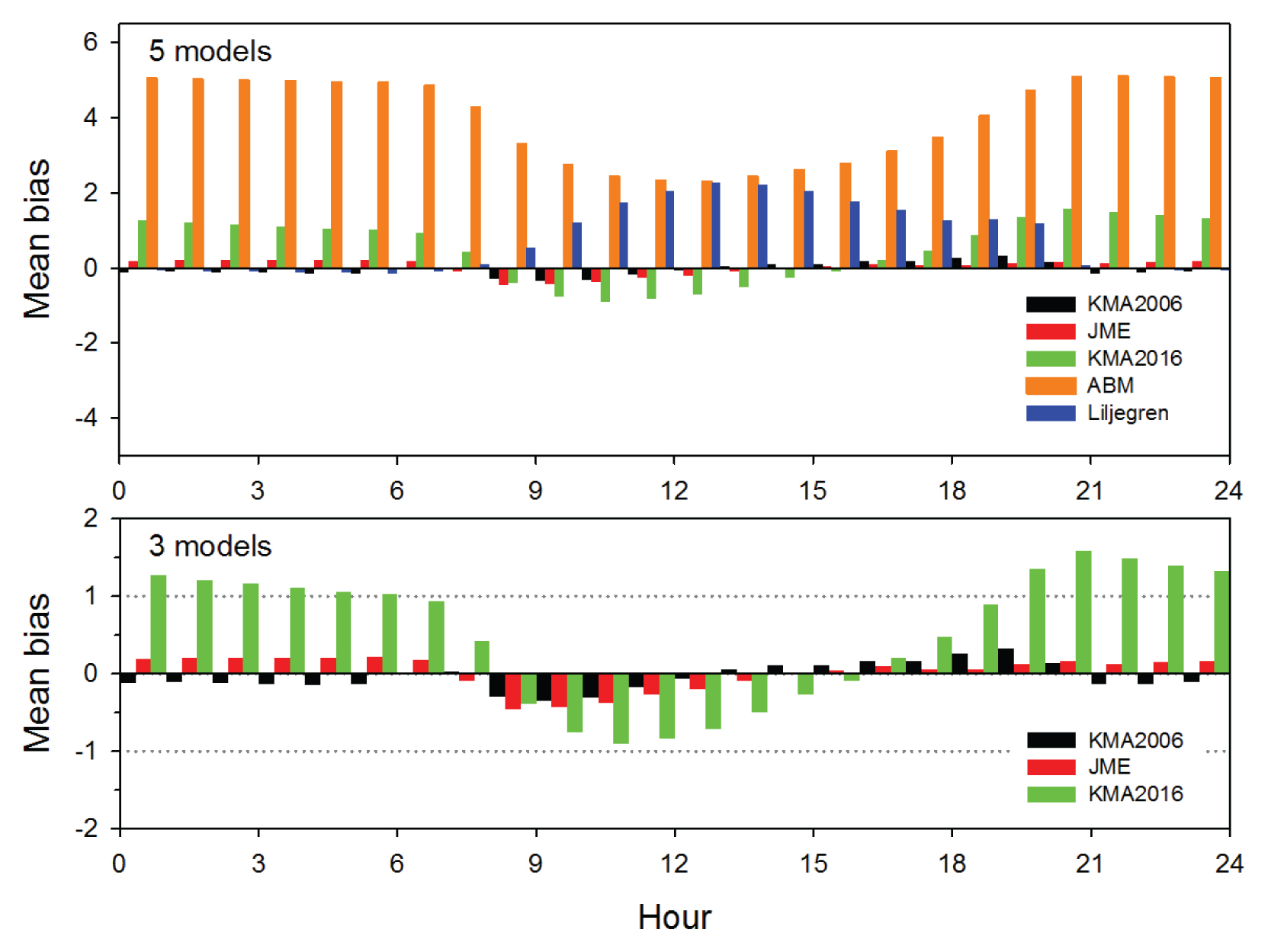
Fig. 4
The Relationship Between Test Variables (temperature, relative humidity, wind speed, solar radiation) and WBGT (observations and estimations). The Other Variables (controlled variable) Except the Test Variable Were Set to the Standard Environment Values
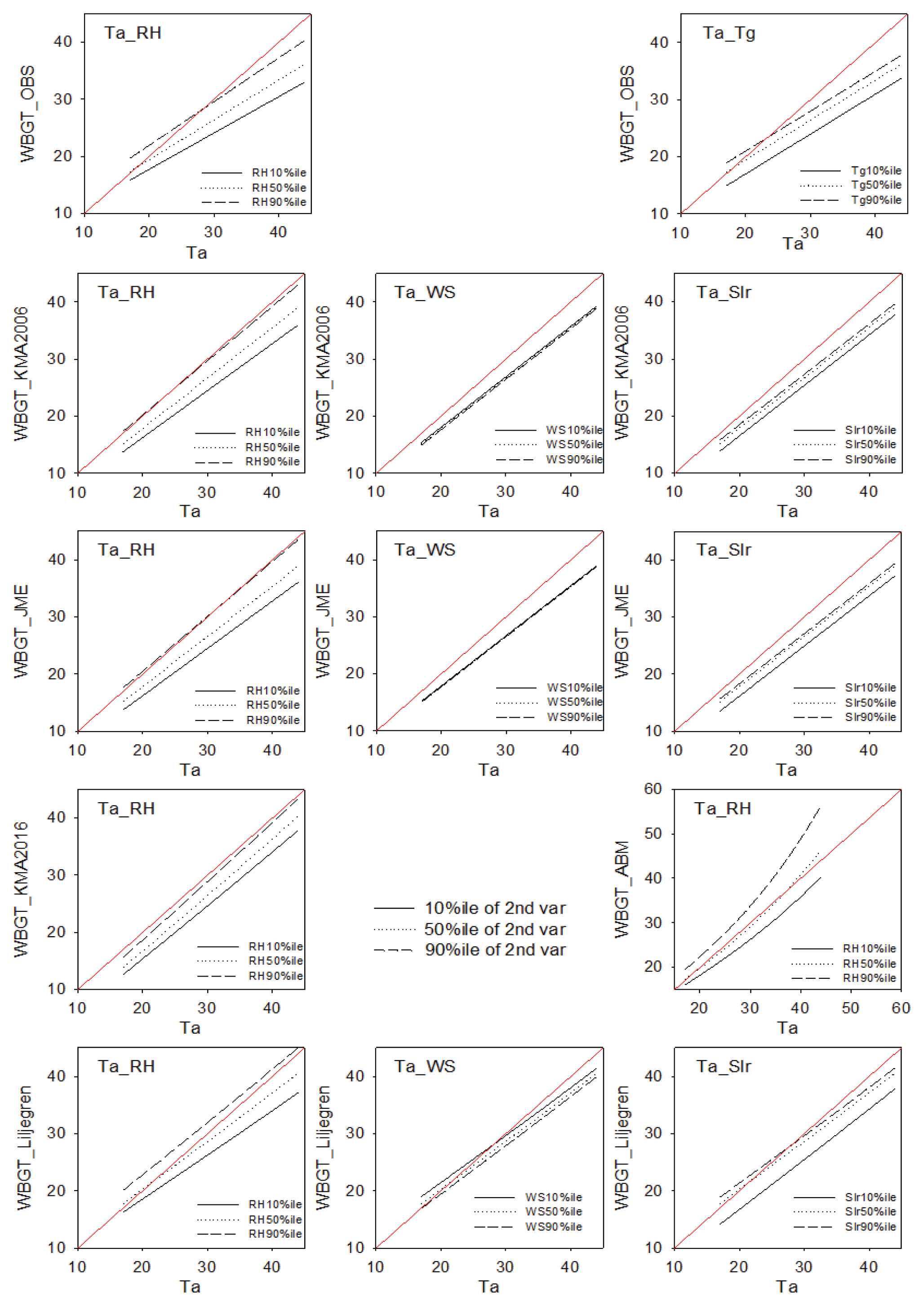
Fig. 5
Diurnal Variations of Wet-bulb Temperature (Tw, °C) and Vapor Pressure (e, hPa) in Seoul Station During Summer (JJAS) from 2016 to 2018
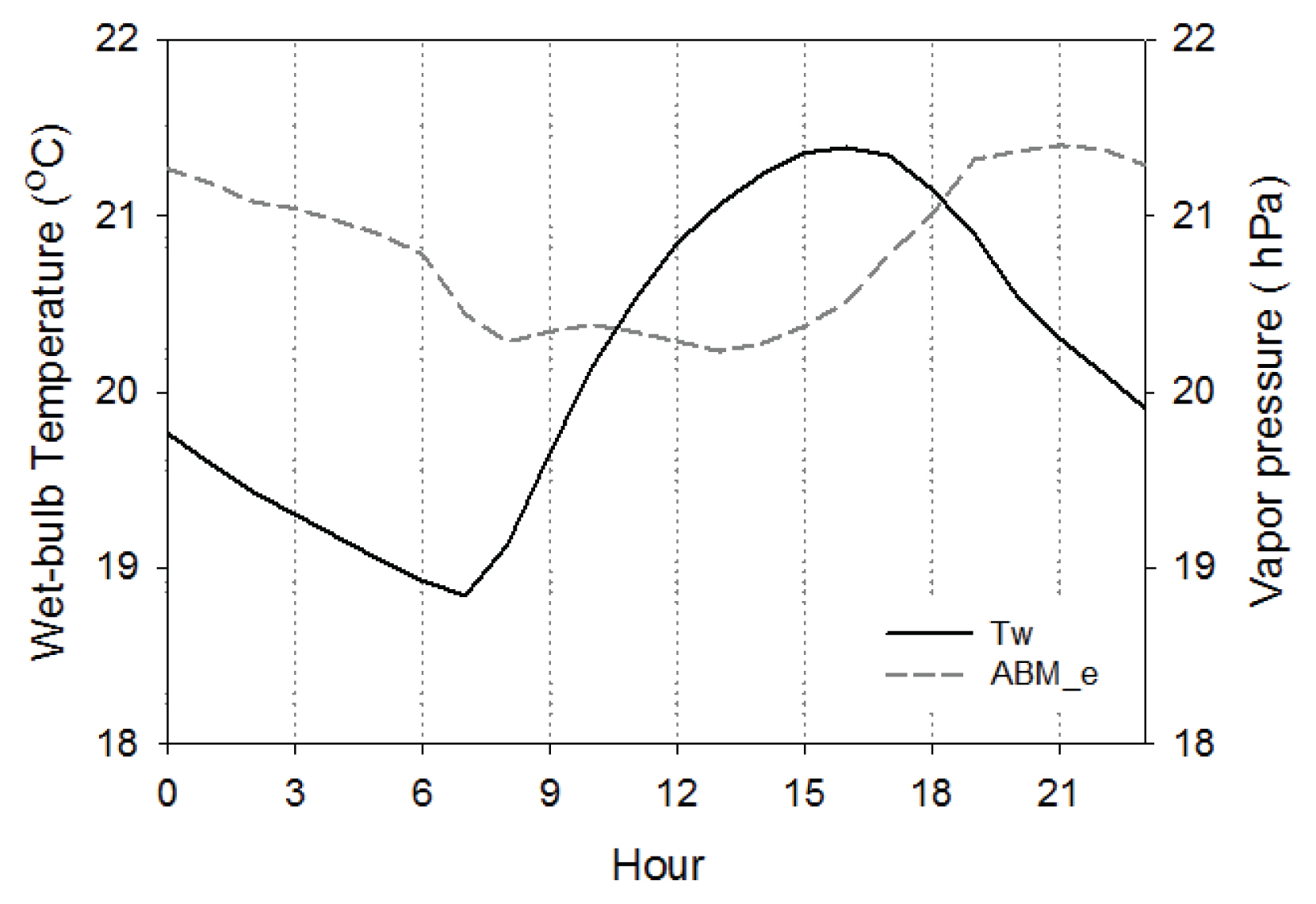
Table 1
Sensor and Associated Equipment Utilized to Observe Globe Temperature
| Equipment | Manufacturer | |
|---|---|---|
| Black globe | C-BB-15cm | Climatec |
| Platinum resistance thermometer | C-PTWP-10 | Climatec |
| Resistive bridge adapter | 4WPB100 | Campbell |
| Data logger | CR800 | Campbell |
Table 2
Correlation Coefficients (r), Mean Bias (MB), and Root Mean Square Error (RMSE) Between Observed and Estimated WBGT from 2016 to 2018
Table 3
Statistics of Meteorological Variables in Seoul at 1500 LST During Summer (JJAS) from 2016 to 2018. The 50%ile Values are Used as the Standard Environment of Each Variable
| Ta (°C) | Slr (MJ m−2) | Tg (°C) | RH (%) | WS (m s−1) | P (hPa) | |
|---|---|---|---|---|---|---|
| 10%ile | 24.1 | 0.5 | 27.5 | 32 | 1.4 | 992.1 |
| 50%ile | 28.8 | 1.8 | 39.8 | 49 | 2.6 | 998.2 |
| 90%ile | 34.1 | 2.7 | 47.6 | 77 | 4.1 | 1004.4 |
| 0.25σ | 0.96 | 0.20 | 1.86 | 4.35 | 0.26 | 1.20 |
Table 4
Variation of WBGT (°C) with a Deviation (0.25σ) of Test Variables (Ta, Slr, Tg, RH, WS, P)
| Ta | Slr | Tg | RH | WS | P | |
|---|---|---|---|---|---|---|
| OBS | 0.94 | - | 0.37 | 0.57 | - | - |
| KMA2006 | 0.85 | 0.14 | - | 0.55 | −0.04 | - |
| JME | 0.84 | 0.11 | - | 0.53 | −0.01 | - |
| KMA2016 | 0.94 | - | - | 0.45 | - | - |
| ABM | 1.03 | - | - | 0.67 | - | - |
| Liljegren | 0.81 | 0.22 | - | 0.59 | −0.23 | 0.00 |
Table 5
Correlation Coefficients (r), Mean Bias (MB), and Root Mean Square Error (RMSE) Between Observed and Estimated WBGT at 1500 LST During the Summer Period of 2018
References
American College of Sports Medicine (ACSM) (1984) Prevention of thermal injuries during distance running: Position stand. Med J Aust, Vol. 141, No. 11–12, pp. 876-879.


Altinsoy, H, and Yildirim, HA (2015) Labor productivity losses over western Turkey in the twenty-first century as a result of alteration in WBGT. Int J Biometeorol, Vol. 59, pp. 463-471.


Australia Bureau of Meteorology (ABM) (2010). Thermal comfort observations. Commonwealth of Australia; Melbourne: Retrieved Mar 9, 2019, from http://www.bom.gov.au/info/thermal_stress/.

Betts, AK, and Ball, JH (1997) Albedo over the boreal forest. Journal of Geophysical Research, Vol. 102, No. D24, pp. 28901-28910.

Cooper, ER, Ferrara, MS, Casa, DJ, Powell, JW, Broglio, SP, Resch, JE, et al (2016) Exertional heat illness in American football players: When is the risk greatest? J Athl Train, Vol. 51, pp. 593-600.



Gaspar, AR, and Quintela, D (2009) Physical modeling of globe and natural wet bulb temperatures to predict WBGT heat stress index in outdoor environments. Int J Biometeorol, Vol. 53, pp. 221-230.


Grundstein, A, and Cooper, E (2018) Assessment of the Australian Bureau of Meteorology wet bulb globe temperature model using weather station data. Int J Biometeorol, Vol. 62, pp. 2205-2213.


ISO 7243 (1989). Hot Environments-Estimation of the heat stress on working man, based on the WBGT-index (wet bulb globe temperature). International Standards Organization, Geneva.

Japan Meteorological Agency (JMA) (2012). Meteorological observation guide (in Japanese). Retrieved from http://www.jma.go.jp/jma/kishou/know/kansoku_guide/tebiki.pdf(気象観測の手引き, 平成 10年 9月, 気象庁).

Japanese Ministry of Environment (JME) (2006). Heat illness prevention information. Retrieved April 19, 2019, from http://www.wbgt.env.go.jp/.

Kakamu, T, Wada, K, Smith, DR, Endo, S, and Fukushima, T (2017) Preventing heat illness in the anticipated hot climate of the Tokyo 2020 summer olympic games. Environ Health Prev Med, Vol. 22, Article No. 68. 10.1186/s12199-017-0675-y.

Korea Meteorological Administration (KMA) (2006). Development of calculation technology for industrial meteorological information in health field - Development of prediction method for Korean activity index. (보건분야 산업기상정보 산출기술개발(III) - 한국형 활동지수 예측기법개발, 기상청).

Korea Meteorological Administration (KMA) (2016). Development of information for life-weather and improvement of its service in 2016. (2016 생활기상정 보 개발 및 서비스개선, 기상청).

Korea Meteorological Administration (KMA) (2018). Standard specification of automatic weather station. KMA Notice No. 2018-3 (In Korean). Retrieved from http://www.law.go.kr/LSW/admRulLsInfoP.do?admRulSeq=2100000112610(자동기상관측장비의 표준 규격. 기상청 고지 제2018-3호, 기상청).

Kysely, J, and Kim, J (2009) Mortality during heat waves in South Korea, 1991 to 2005: How exceptional was the 1994 heat wave? Clim Res, Vol. 38, pp. 105-116.

Lee, J-S, Byun, H-R, and Kim, D-W (2016) Development of accumulated heat stress index based on time-weighted function. Theor Appl Climatol, Vol. 124, pp. 541-554.

Lee, SW, Lee, K, and Lim, B (2018) Effects of climate change-related heat stress on labor productivity in South Korea. Int J Biometeorol, Vol. 62, No. 12, pp. 2119-2129.


Lemke, B, and Kjellstrom, T (2012) Calculating workplace WBGT from meteorological data: A tool for climate change assessment. Ind Health, Vol. 50, No. 4, pp. 267-278.


Liljegren, JC (2008). Wet bulb globe temperature (WBGT) software program (Version 1.1). Argonne National Laboratory, Chicago, IL: (Fortran language source code available per request to jcliljegren@anl.gov).

Liljegren, JC, Carhart, RA, Lawday, P, Tschopp, S, and Sharp, R (2008) Modeling the wet bulb globe temperature using standard meteorological measurements. J Occup Environ Hyg, Vol. 5, pp. 645-655.


McGregor, GR, Bessmoulin, P, Ebi, K, and Menne, B (2015). Heatwaves and health: Guidance on warning-system development. World Meteorological Organization and World Health Organisation, WMO-No 1142. p 1-96.

Ono, M, and Tonouchi, M (2014) Estimation of wet-bulb globe temperature using generally measured meteorological indices. Jpn J Biometeor, Vol. 50, pp. 147-157 (in Japanese with English abstract).

Park, S-A, Kong, HY, Kim, S-H, Park, S, and Shin, Y-K (2016) Characteristics of thermal variations with the different land covers in an urban area. Ecology and Resilient Infrastructure, Vol. 3, No. 1, pp. 46-53.

Patel, T, Mullen, SP, and Santee, WR (2013) Comparison of methods for estimating Wet-Bulb Globe Temperature index from standard meteorological measurements. Mil Med, Vol. 178, No. 8, pp. 926-933.


Smith, MT, Reid, M, Kovalchik, S, Woods, TO, and Duffield, R (2017) Heat stress incident prevalence and tennis matchplay performance at the Australian Open. J Sci Med Sport, Vol. 21, No. 5, pp. 467-472.


- TOOLS
-
METRICS

-
- 4 Crossref
- 4,285 View
- 216 Download





