|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(7); 2018 > Article |
|
Abstract
In this study, non-stationary GEV models with meteorological variables were developed for extreme daily rainfall depths. The scale parameter of the GEV distribution is regarded as a function of the covariate. The meteorological variables selected in this study were surface air temperature (SAT) and dew point temperature (DPT), which are suitable for future climate change scenarios. The data were collected from Seoul Station, and were analyzed using monthly maximum daily rainfall data from July and August (summer season). Various models were constructed to select the most appropriate covariate (SAT and DPT) function for the scale parameter of the GEV distribution, and the model with the minimum Akaike Information Criterion value was selected as the optimal model. As a result of the analysis, the model with A • S A T t B
요지
본 연구에서는 극한 일강우량을 대상으로 기상 변수가 포함된 비정상성 GEV 모형이 개발되었다. 이 때 GEV 분포의 매개변수 중 축적매개변수를 공변량의 함수로 적용하였다. 본 연구에서 선택된 기상변수들은 추후 기후변화 시나리오를 적용하기에 용이한 지표면 기온(Surface air temperature, SAT)과 이슬점 온도(Dew point temperature, DPT)이다. 기상청 지점 중 서울 지점 자료를 대상으로, 7월부터 8월까지(여름철)의 월 최대 일 강우량 시계열을 이용하여 분석을 수행하였다. GEV 분포의 축척 매개변수를 위한 최적 공변량(기온과 이슬점) 함수를 선택하기 위하여 다양한 모델을 구성하였으며, 구성된 모델 중 AIC(Akaike Information Criterion)가 가장 작은 모델을 최적 모델로 선정하였다. 분석 결과, A • S A T t B
기후변화에 따라 수반되는 극한 강우사상의 예상되는 변화는 사회경제적으로 부정적인 영향을 줄 가능성이 매우 높기 때문에 특별히 많은 관심이 주어진다(Kunkel et al., 1999). IPCC AR5 기후변화 시나리오에 따라 수많은 GCMs 및 RCMs로부터 전망된 미래 기후는 극한 강우의 증가, 광범위한 지역에서의 홍수 발생을 경고하고 있다.
빈도해석방법은 극한 강우의 크기를 발생 확률과 관련시키기 위해 널리 사용되어왔다. 그러나 이러한 전통적 빈도해석방법은 기후변화의 영향을 분석하려는 관점에서 보면 초과확률과 재현기간이라는 용어 자체가 기후변화를 반영한 비정상상태에서는 더 이상 유효한 개념이 아니기 때문에, 극한강우를 확률적으로 해석하기 위한 새로운 방법이 필요하게 된다. 빈도해석에서 비정상성을 고려하는 한 가지 방법은 확률분포형의 매개변수를 기후와 관련된 변수의 함수로 만드는 것인데, 특히 GCMs 혹은 RCMs에서 모의되는 대규모 대기 순환을 반영한 기상변수가 적용된다면 기후변화에 대한 국지적인 극한 강우의 영향을 살펴보는데 유용하게 적용될 수 있을 것이다(Tramblay et al., 2013). 그러나 비정상성 빈도해석 분야에서는 그동안 확률분포형의 매개변수를 단지 시간의 함수로 표현한 연구가 주로 이루어져왔으며(Kim et al., 2017), 확률분포형의 매개변수를 기상자료의 함수로 표현한 연구는 일부에 불과한 실정이다.
최근 일부 연구에서 연 최대 시계열을 대상으로 기상변수를 이용한 비정상성 GEV 분포를 적용한 사례를 살펴볼 수 있다(El Adlouni et al., 2007; Pujol et al., 2007). Aissaoui-Fqayeh et al. (2009)은 기상변수로서 남방진동지수를 적용하여 미국 캘리포니아의 연 최대 강수량 시계열의 비정상성 GEV 모델을 개발하였다. Villarini et al. (2012)은 또한 극치분포의 매개변수를 북대서양 진동지수와 지중해 지수의 함수로 표현하여 강수량과 홍수량의 빈도해석을 수행한 바 있다.
본 연구의 목적은 기상청 서울 지점에서 관측된 극한 강우사상을 대상으로 기상 변수가 포함된 비정상성 GEV 모형을 개발하는 것이다. 본 연구에서 선택된 기상변수들은 지표면 기온과 이슬점 온도이며, 미래 기후변화를 반영하였을 경우를 상정한 분석 방법의 예시가 제시된다. 미래 기후를 모의하기 위해 사용되는 미래 기후변화 시나리오는 기온의 변화 패턴은 상대적으로 일관성 있고 신뢰성 있게 전망하고 있지만, 극한 강우는 아직까지 일관성 있고 신뢰성 있는 전망결과를 제공하고 있지 못하기 때문에(O'Gorman, 2012), 기상변수를 반영한 비정상성 빈도해석에 의한 접근방법은 극한 강우에 대한 기후변화의 영향을 살펴보기 위한 합리적인 방법이 될 수 있을 것이다.
본 연구에서는 기상청 서울지점 일 기상자료가 이용되었다. 빈도해석을 수행하기 위하여 1961년부터 2017년까지 7월에서 8월까지의 일 강우량 자료를 이용하여 7월과 8월 최대 일 강우량 시계열을 추출하였다. 또한 동 시기의 일 지표면 기온(SAT) 및 일 이슬점(DPT) 자료가 비정상성 빈도해석 시 기상변수로 각각 적용되기 위하여 추출되었다.
GEV 분포의 누가확률분포함수 FGEV는 Eq. (1)과 같이 정의된다.
여기서 x은 매년 7월과 8월의 최대 일 강수량이며, α는 축척 매개변수(scale parameter), β는 형상 매개변수(shape parameter), xo는 위치 매개변수(location parameter)이다. 변수 x의 범위는 형상 매개변수 β의 부호에 따라 결정되며, β<0일 때 모든 매개변수들은 모든 x에 대하여 xo+α/β<x<∞의 범위에 있어야만 극한 강우량의 빈도해석에 적절하다(Lee, 2009). 이러한 제약조건이 반영되어 추후 매개변수 추정이 수행되었다.
다양한 방법들이 GEV 분포의 매개변수를 추정하기 위하여 사용될 수 있으나, 본 연구에서는 GEV 분포의 매개변수들 중 일부가 기상변수의 함수로 표현될 경우에 매개변수 추정이 상대적으로 용이한 최우도법을 적용하였다. 매개변수 추정은 아래와 같은 음 대수 우도 함수(negative log-likelihood function) nllh을 최소화하는 최적화 기법을 이용하여 수행되었으며, 본 연구에서는 최적화 기법으로 유전자 알고리즘이 적용되었다. 물론, 상기 언급한 매개변수들의 제약조건이 최적화 기법 수행과정에 포함되었다.
여기서 n은 자료의 개수이다.
최적화 과정을 통하여 매개변수들이 추정되고 나면, 특정비 초과확률 1-p에 대응하는 극한 강우량 x(1-p)은 Eq. (1)의 역함수를 구하여 아래와 같이 계산된다.
여기서 p는 초과확률로서 0<p<1의 범위를 갖는다.
본 연구에서 GEV 분포의 매개변수는 서울지점의 여름철(7월과 8월) 월 최대 일 강우량 시계열 관측자료를 이용하여 추정되었다. 일반적인 극값 통계는 연 단위로 분석되어 연 최대시계열(즉, 일 년에 하나의 자료)을 추출하여 수행되지만, 연 최대 시계열만을 이용할 경우 자료 개수가 작음에 따라 매개변수를 적절하게 추정하기 어려운 문제가 있다(Hosking, 1990). 따라서 본 연구에서는 이를 보완하기 위하여 매년 7월과 8월에 각각 최대 일 강우량 시계열을 구축함으로써 57년 자료에서 114개의 자료를 추출하여 이후 분석을 수행하였다.
전통적으로, GEV 분포는 관측자료의 근본적인 프로세스가 서로 독립적이고 같은 분포로 구성되었으며, 시간에 따라 변하지 않는 정상성을 가정한다. 그러나 이러한 가정은 비정상성을 설명하기 위하여 기상변수를 도입함으로써 완화될 수 있다. 예를 들어, GEV 분포의 매개변수들 중 일부는 기상변수의 함수로 표현될 수 있다. 이론적으로는 GEV 분포의 모든 매개변수들이 각자 다양한 기상변수들의 함수로 표현될 수 있으나, 본 연구에서는 아래와 같이 축적 매개변수 α가 기상변수의 함수인 것으로 표현하였다.
또는
여기서 매개변수 A와 B은 Eq. (2)의 음의 대수 우도함수를 최소화하는 과정에서 추정된다. 최적화 과정으로부터 결정되는 GEV 분포의 축적 매개변수 α는 기상변수 z의 함수가 되므로 시간에 따라 변화되는 값을 갖게 된다.
지표면 기온과 이슬점은 극한 강우량과 강한 scaling 관계가 있는 것으로 보고된 것에 착안하여(Lepore et al., 2015), 일 최대 강수량이 발생한 날과 관련된 지표면 기온과 이슬점이 일 강우량의 비정상성 빈도해석을 위한 기상변수로 적용되었다. 이 때, 우리나라와 같은 몬순 기후대의 경우 강우 시의 냉각 효과로 인하여 일 최대 강수량이 발생한 날을 포함한 수 일 전의 기상 자료가 해당 일의 강수량에 영향을 미칠 수 있기 때문에(Ali and Mishra, 2017), 일 최대 강수량이 발생한 당일부터 2일 전 날까지의 지표면 기온(또는 이슬점) 중 가장 큰 값이 일 최대 강수량과 관련이 있을 것으로 판단하였다. 또한, 절대적인 지표면 기온(또는 이슬점)을 비정상성 빈도해석에 직접 적용하기 보다는 시기별 특성을 고려하는 것이 수문기상학적으로 더 타당하다는 연구결과에 착안하여(Lee and Kim, 2018), 해당 월의 지표면 기온(또는 이슬점)의 확률분포 상에서 일 최대 강수량과 관련이 있는 것으로 결정된 지표면 기온(또는 이슬점)의 비초과확률을 비정상성 빈도해석을 위한 기상변수 z(t)로 적용하였다.
이와 같은 방법으로 지표면 기온 및 이슬점을 이용하여 Table 1과 같은 모델을 구성하여 연구를 진행하였다: (1) 정상성 GEV, (2) 지표면 기온의 지수함수를 적용, (3) 지표면 기온의 멱함수를 적용, (4) 이슬점의 지수함수를 적용, (5) 이슬점의 멱함수를 적용.
위 다섯 개의 모델들 중에서 AIC (Akaike Information Criterion)를 최소화하는 모델을 최적 모델로 선정하는 것으로 하였으며, AIC는 아래와 같이 계산된다(Akaike, 1974).
여기서 nllh은 Eq. (2)로부터 결정되며, K은 모델의 매개변수의 개수로서 정상성 모델의 경우에는 K=3, 비정상성 모델의 경우에는 K=4이다.
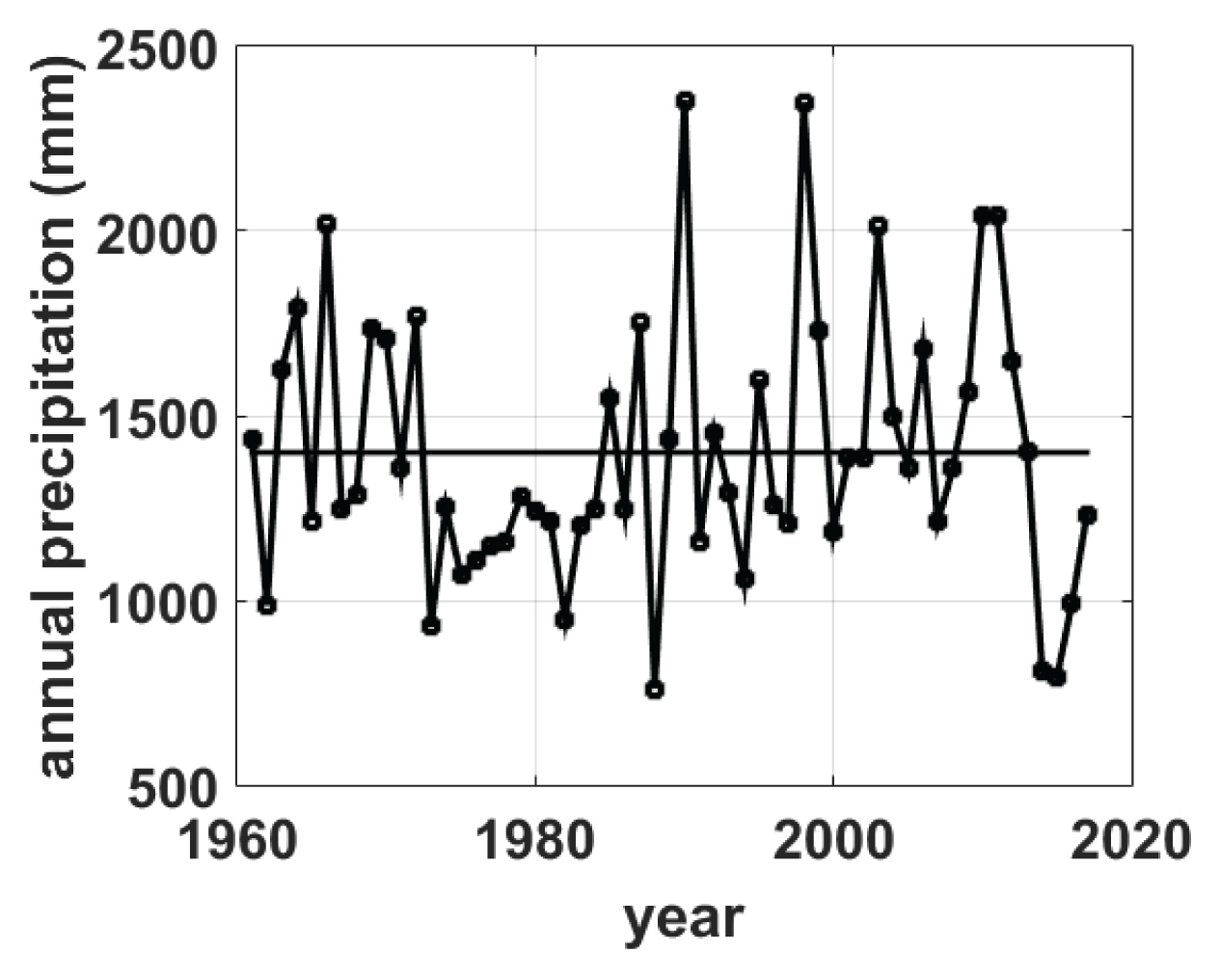
Fig. 1에 서울지점 연강수량을 도시하였다. 1961년부터 2017년까지 서울지점 연평균 강수량은 1,400 mm이며, 표준편차는 360 mm이다. 최소 연강수량은 1988년 761 mm로 기록되었으며, 최대 연 강수량은 2,356 mm로 1990년에 기록되었다. 최근 10년(1998년 - 2017년) 동안의 연 강수량은 1,388 mm로 과거에 비해 약간 감소한 것으로 조사되었다.
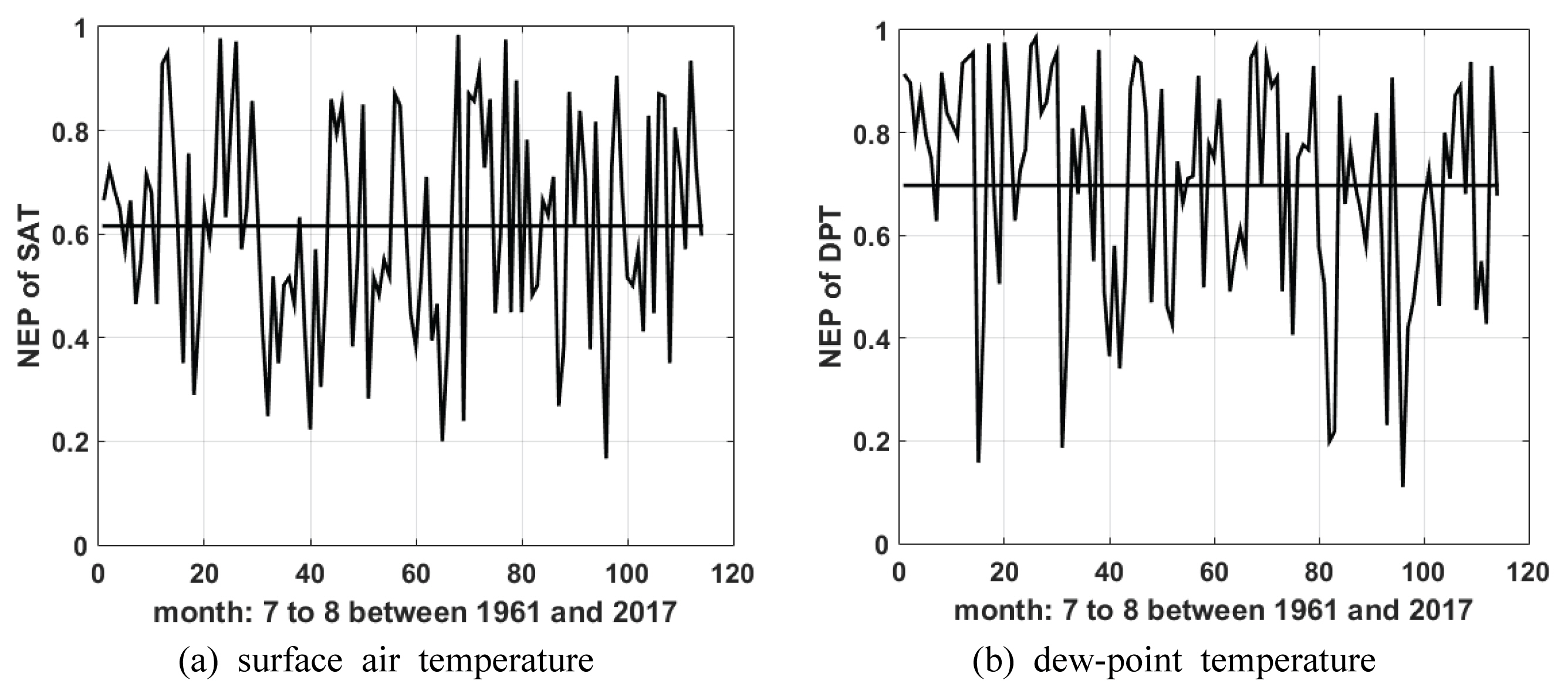
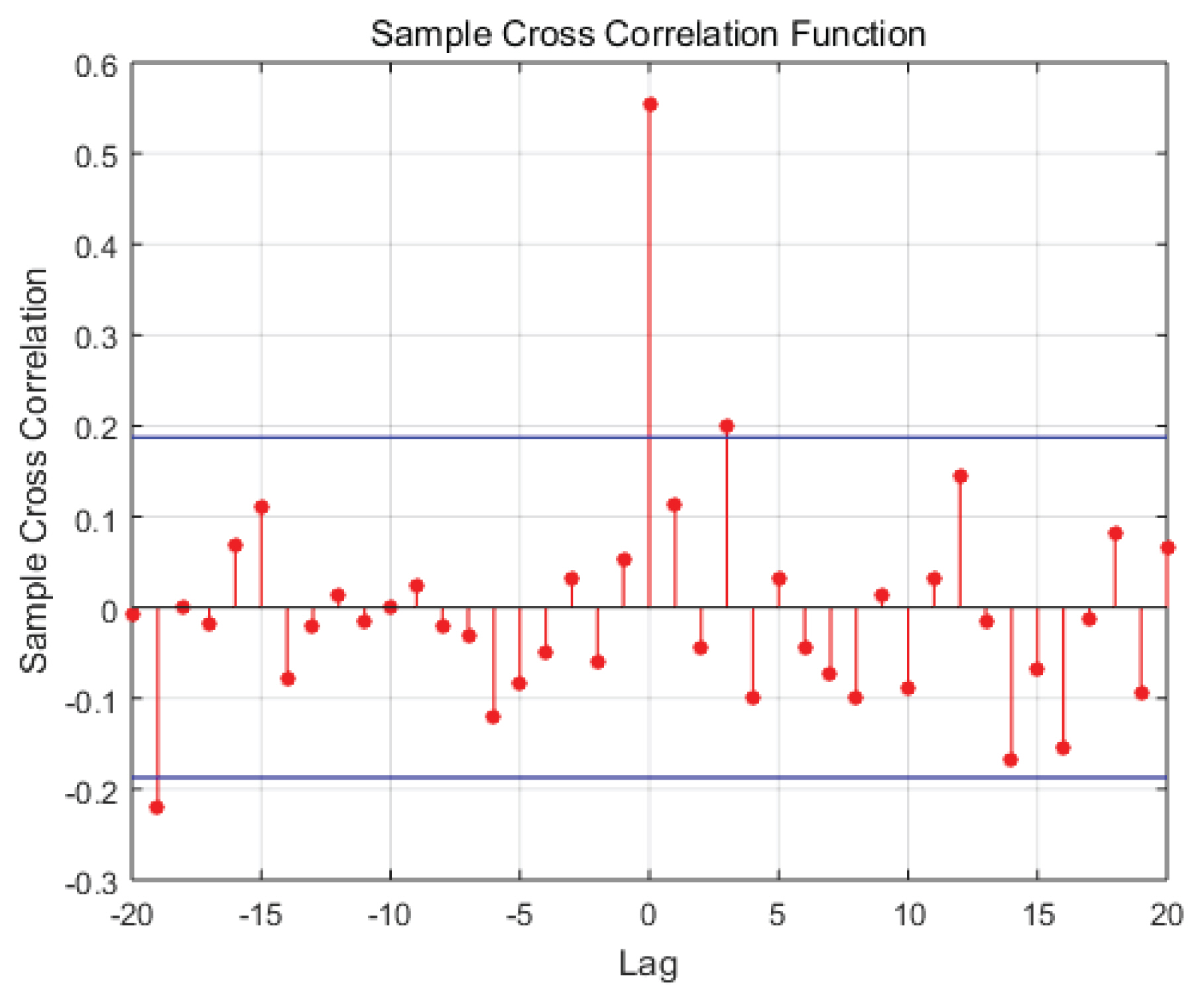
Fig. 2는 서울지점 7월과 8월의 월 최대 일강수량에 대응하는 지표면 기온과 이슬점 비초과확률의 시계열을 보여주고 있다. 전술한 바와 같이 월 최대 일 강수량이 발생한 날을 기준으로 선행 2일까지의 값들 중 가장 큰 값을 해당 월 최대 일 강수량에 대응하는 지표면 기온(또는 이슬점)으로 선택하였다. 참고로 비초과확률은 해당 월에 기록된 지표면 기온(또는 이슬점)을 이용하여 matlab의 ksdensity 함수를 이용하여 비매개변수적으로 계산되었다. 지표면 기온과 이슬점 시계열 사이의 교차상관계수는 0.5 이상으로 매우 큰 상관성이 있는 것으로 조사되었다(Fig. 3 참조). 이와 같이 두 시계열 사이에 큰 상관성이 있기 때문에 추후 비정상성 빈도해석 수행 시에 지표면 기온과 이슬점을 동시에 기상변수로 적용하는 것으로 적절하지 않을 것으로 판단되었다.
Figs. 4와 5는 분위 회귀분석을 이용하여, 서울 지점 7월과 8월 지표면 기온과 이슬점에 대응하는 95% 극한 강우량의 회귀 경사를 추정한 결과를 각각 나타내고 있다. 참고로 분위 회귀분석에서 주어진 분위수 τ(본 연구의 경우 0.95)에 대한 분위 회귀식은 아래와 같이 표현된다.
여기서 xi은 일 강우량이며, zi은 xi에 대응하는 지표면 기온(또는 이슬점)이다. 따라서 지표면 기온(또는 이슬점)이 1 ℃ 상승할 때 일 강우량 변화율 (%)인 회귀 경사는 지수 변환을 통하여 아래와 같이 구할 수 있다.
Fig. 4에 도시한 바와 같이 극한 강우량과 지표면 기온 사이의 회귀 경사는 강우 당일 및 하루 전일 지표면 기온의 경우에는 강우 시의 냉각효과로 인하여 -19.4% 및 -2.59%로 지표면 기온이 상승 시 극한 강우량은 감소하는 것으로 나타났으며, 2일 전 및 3일 전의 지표면 기온의 경우에는 1.81% 및 0.681%로 지표면 기온 상승 시 극한 강우량이 증가하는 것으로 나타냈다. 그러나 기온이 1 ℃ 상승할 경우 대기 중의 수분 함유 가능 용량의 증가로 인하여 극한 강우량은 6% 정도 상승하는 Clausius-Clapeyron 관계에는 훨씬 못 미치는 변화율을 보임을 나타내고 있다. Fig. 5는 극한 강우량과 이슬점 사이의 분위 회귀분석 결과를 보여주고 있다. 강우 당일의 이슬점에 대한 극한 강우량의 변화율이 Clausius-Clapeyron 관계와 가장 유사함을 살펴 볼 수 있다.
이러한 결과만 살펴보면, 비정상성 빈도해석을 위한 기상변수로 지표면 기온보다는 이슬점이 더 타당할 것이라는 예상을 해 볼 수 있으나, 여러 관련 연구들의 경우 지표면 기온을 기상변수로 적용하는 사례가 더 빈번하므로 일단 지표면 기온과 이슬점 둘 모두를 적용 가능 기상변수로 간주하고, 이후 분석을 수행하였다.
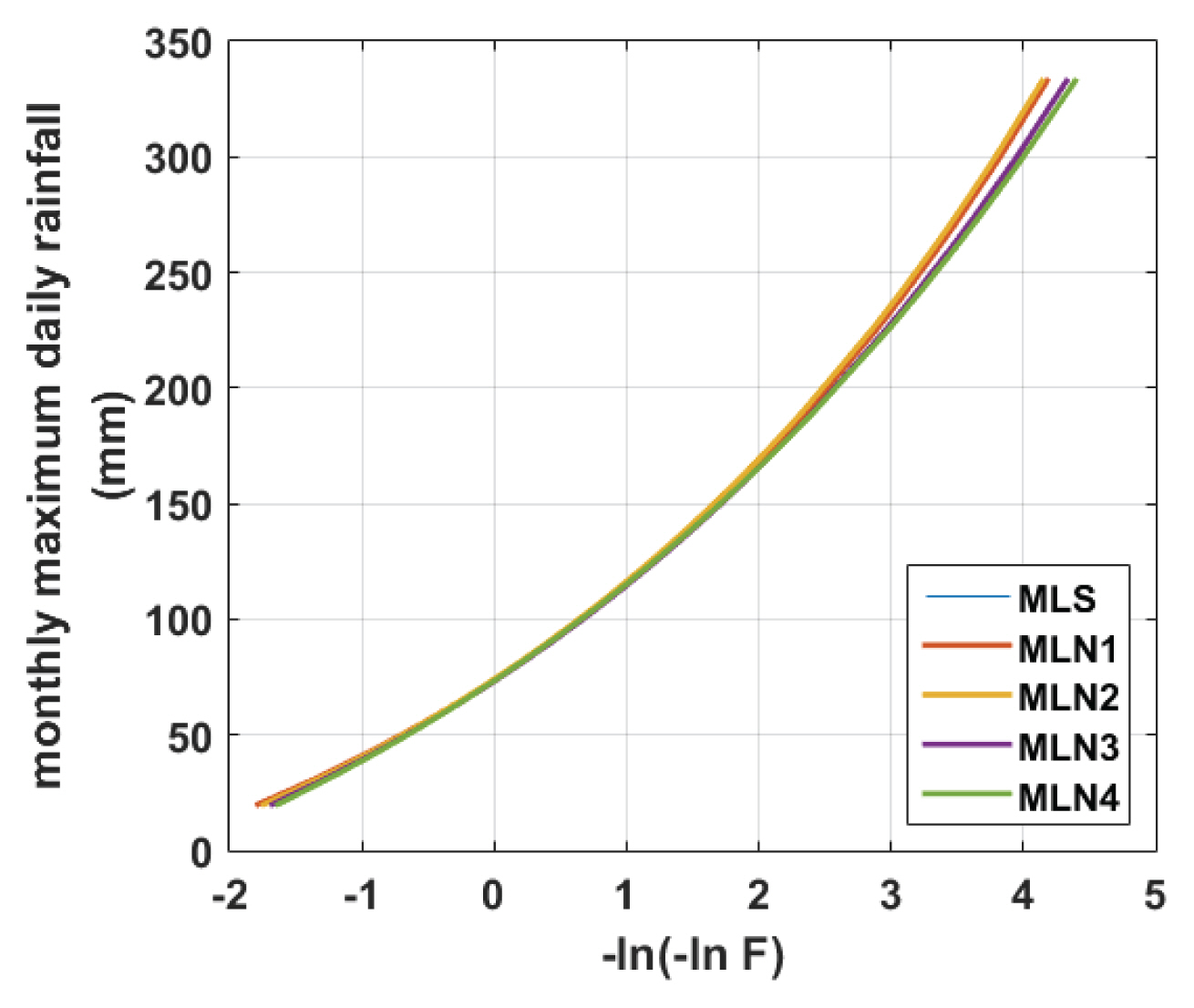
일 강우량의 비정상성 빈도해석을 위한 기상변수로 지표면 기온 또는 이슬점을 고려한 GEV 분포가 7월과 8월 월 최대 일 강우량 시계열에 대하여 적합되었다. 다섯 개 모델에 대한 매개변수와 AIC을 Table 1에 나타내었으며, 각각의 모델에 의해 작성된 누가확률밀도함수를 Fig. 6에 도시하였다. Fig. 6에서 ‘MLS’은 최우도법을 이용하여 정상성 GEV 분포를 적합한 결과이다. ‘MLN1’은 최우도법을 이용하여 α t = e x p ( A + B · S A T t ) α t = A · S A T t B α t = e x p ( A + B · D P T t ) α t = A · D P T t B
Table 1의 AIC 결과에서 알 수 있듯이, 아래와 같이 GEV 분포의 축적 매개변수가 지표면 기온의 멱함수로 표현되는 모델이 최종적으로 선정되었다.
정상성 모델과 비정상성 모델의 결과를 서로 비교하기 위하여 비초과확률 95%, 99%, 99.5%에 해당하는 일 강우량을 Fig. 7에 관측자료와 함께 도시하였다. Fig. 7에서 ‘obs’는 관측된 여름철 월 최대 일 강우량이다. 당연히 정상성 모델의 비초과확률에 대한 확률강우량은 시간에 따라 변하지 않으므로, 수평선으로 나타나게 된다(Fig. 6에서 점선). 반면에 비정상성 모델의 경우에는 지표면 기온의 변화에 따라 비초과확률에 해당하는 일 강우량이 다양한 값을 갖게 됨을 살펴볼 수 있다(Fig. 7의 실선).
지표면 기온 변화에 따른 확률강우량의 변화는 최대 일 강수량이 작게 온 달(2008년 8월 72.5 mm)과 많이 온 달(2001년 7월 273.4 mm)의 정상성 모델과 비정상성 모델의 확률밀도함수를 비교함으로써 더 명확하게 설명될 수 있다(Fig. 8 참조). 상대적으로 작은 최대 일 강수량을 기록한 월의 비정상성 확률밀도함수는 정상성 확률밀도함수와 비교해볼 때 mode는 거의 같은 값을 가지지만 퍼짐정도가 훨씬 작은 것으로 알 수 있다. 반대로 상대적으로 큰 최대 일 강수량을 기록한 월의 비정상성 확률밀도함수는 정상성 확률밀도함수와 비교해볼 때 mode는 거의 같은 값을 가지지만 퍼짐정도가 더 큰 것을 살펴볼 수 있다. 이는 GEV 분포의 축적 매개변수를 살펴보면 쉽게 이해될 수 있다. 정상성 모델의 축적 매개변수 값 37.4146을 기준으로 2008년 8월의 비정상성 모델의 축적 매개변수 값은 24.4079이며, 2011년 7월의 비정상성 모델의 축적 매개변수 값은 43.9681이다. 자료가 GEV 분포를 따를 경우 자료의 표준편차가 커질수록 축적 매개변수가 커지기 때문이다. 즉, 본 연구에서 선택한 비정상 모델의 경우 높은 지표면 기온일수록 축적 매개변수가 커지는 형태이며, 이는 정상성 모델의 개념으로 보면 자료의 표준편차를 증가시키는 역할을 하게 된다. 지표면 기온에 따른 축적 매개변수의 변화는 비초과확률에 해당되는 확률강우량을 살펴볼 경우에도 명확하게 살펴볼 수 있다. Fig. 8에 도시한 바와 같이, 99.5% 비초과확률을 기준으로 2008년 8월 지표면 기온에 대한 비정상성 모델의 확률강우량은 324.3 mm이며, 정상성 모델의 확률강우량은 429.7 mm (지표면 기온에 무관), 2011년 7월 지표면 기온에 대응하는 비정상성 모델의 확률강우량은 524.7 mm임을 알 수 있다. 즉, 지표면 기온이 증가할수록 GEV 분포의 축적 매개변수가 커짐에 따라 자료의 표준편차가 동반하여 증가하게 되므로, 확률강우량도 증가하게 된다.
확률밀도함수의 변화는 정상성 모델의 특정 비초과확률에 해당하는 확률강우량을 초과하는 확률을 살펴봄으로써 정량화될 수도 있다. 예를 들어서, 정상성 모델에서 x90은 178.0 mm이며, 이에 대응하는 초과확률은 당연히 10%이다(Table 2 참조). 하지만 비정상성 모델에서는 일 최대 강우량이 상대적으로 낮은 달(2008년 8월)과 높은 달(2001년 7월)에서 178.0 mm를 초과할 확률이 각각 4.77%에서 13.64%까지 변화될 수 있음을 살펴볼 수 있으며, 다른 비초과확률에 대해서도 또는 다른 특정 월에 대해서도 유사한 결과를 얻을 수 있다.
Fig. 9는 미래 기온 상승에 따른 영향 분석의 예를 도시하고 있다. Fig. 9에서 ‘present’는 관측된 지표면 기온을 이용하여 산출한 99% 비초과확률에 해당하는 확률강우량의 분포를 나타내고 있으며, “SAT 1 ℃-up”은 미래 지표면 기온이 1 ℃ 상승하였을 경우에 대응하는 99% 비초과확률에 대응하는 확률강우량의 분포이다. “SAT 3 ℃-up”는 미래 지표면 기온이 3 ℃ 상승하는 경우의 분포이다. 서울지점의 경우 지표면 기온이 증가함에 따라 확률강우량이 증가할 가능성이 매우 높음을 살펴볼 수 있다. 또한, 기상변수를 고려한 비정상성 모델을 구성할 경우 기상변수의 분포에 따른 확률강우량의 확률분포함수를 직접 구성할 수 있게 되므로, 기후변화에 따른 확률강우량 추정의 불확실성을 정량적으로 분석하는데 효과적일 것으로 판단된다.
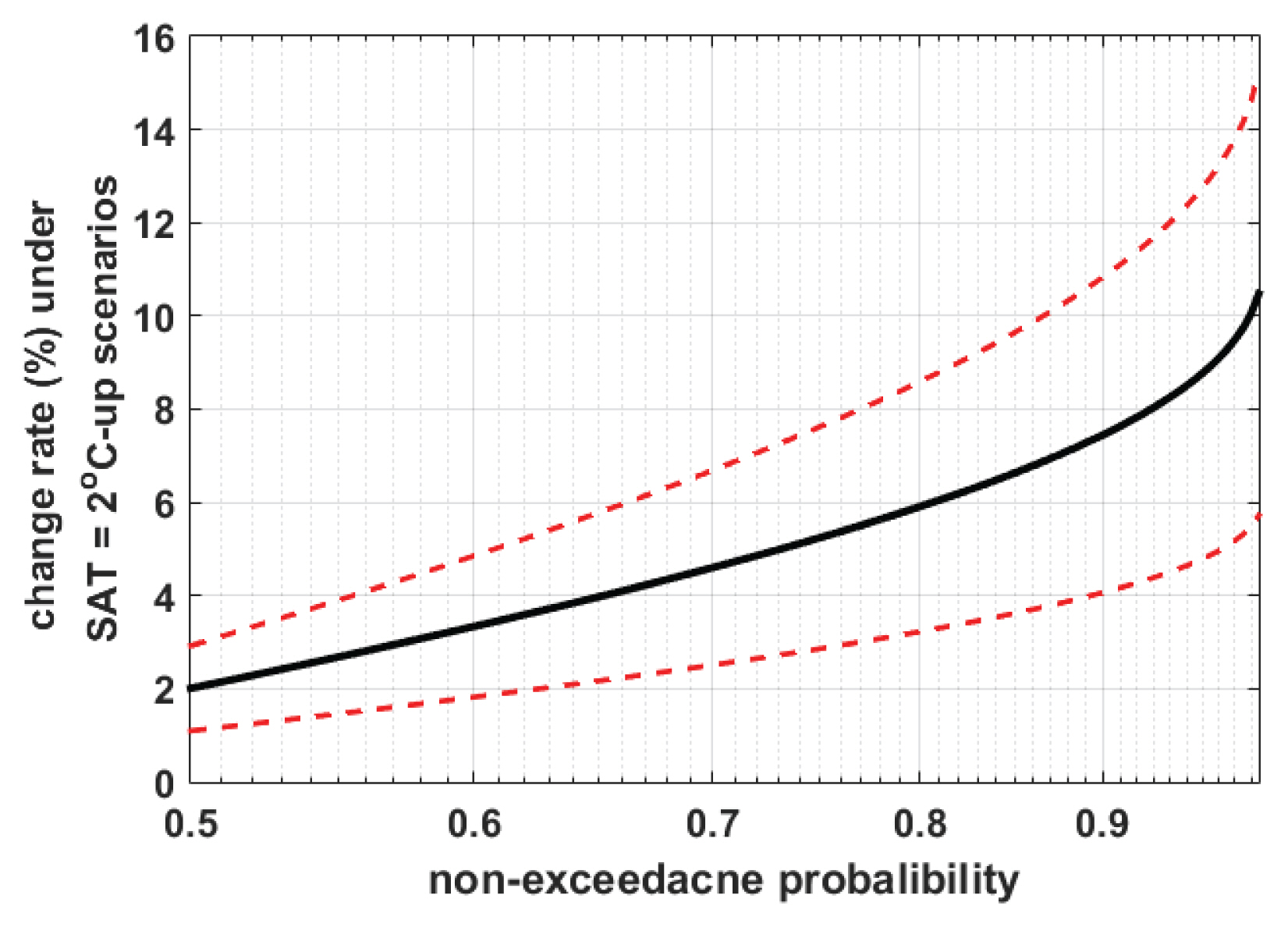
Fig. 10은 미래 지표면 기온이 2 ℃ 상승하였을 경우에 다양한 비초과확률에 대응하는 확률강우량의 변화율을 도시하고 있다. 그림에서 실선은 평균적인 변화율을, 점선은 아래 위로 각각 평균적인 변화율의 표준편차를 의미한다. 비초과확률이 증가할수록 변화율도 같이 증가하고 있으며, 재현기간이 커질수록 확률강우량이 더 큰 폭으로 증가할 가능성이 높음을 알 수 있다. 변화율의 표준편차로 정량화한 지표면 기온 상승에 대한 불확실성 또한 비초과확률이 커질수록 동반하여 증가함을 살펴볼 수 있다.
기후변화에 따라 수반되는 극한 강우사상의 예상되는 변화는 사회경제적으로 부정적인 영향을 줄 가능성이 매우 높다. 빈도해석방법은 극한 강우의 크기를 발생 확률과 관련시키기 위해 널리 사용되었다. 그러나 이러한 전통적인 빈도해석방법은 기후변화의 영향을 분석하려는 관점에서 보면 초과확률과 재현기간이라는 용어 자체가 기후변화를 반영한 비정상상태에서는 더 이상 유효한 개념이 아니기 때문에, 극한강우를 확률적으로 해석하기 위한 새로운 방법이 필요하게 된다.
이에 본 연구에서는 극한 강우사상을 대상으로 기상 변수가 포함된 비정상성 GEV 모형을 개발하고자 하였다. 이때 GEV 분포의 매개변수 중 축적매개변수를 공변량의 함수로 적용하였다. 본 연구에서 선택된 기상변수들은 추후 기후 변화 시나리오를 적용하기에 용이한 지표면 기온과 이슬점 온도이며, 미래 기후변화를 반영하였을 경우를 상정한 분석방법의 예시가 제시되었다. 기상청 지점 중 서울 지점 자료를 대상으로 하였으며, 기존의 극값 통계 시 연단위로 분석되어 일 년에 하나의 자료를 추출하여 수행하나 매개변수 추정이 어려운 문제점이 있음에 따라, 본 연구에서는 7월부터 8월까지(여름철)의 월 최대 일 강우량 시계열을 이용하여 분석을 수행하였다.
비정상성 빈도해석 이전 지표면 기온 자료와 이슬점 자료의 극한강우량 관계를 살펴보기 위해 일 최대 강수량이 발생한 당일부터 2일 전 날까지의 지표면 기온(또는 이슬점) 중 확률분포 상에서 일 최대 강수량과 관련이 있는 것으로 결정된 지표면 기온(또는 이슬점)의 비초과확률을 비정상성 빈도해석을 위한 기상변수로 적용하고자 하였다. 비정상성 빈도 해석을 위해 모델을 구성한 결과는 다음과 같다. (1) 정상성 GEV, (2) 지표면 기온의 지수함수를 적용, (3) 지표면 기온의 멱함수를 적용, (4) 이슬점의 지수함수를 적용, (5) 이슬점의 멱함수를 적용. 위 다섯 개의 모델들 중에서 AIC(Akaike Information Criterion)를 최소화하는 모델을 최적 모델로 선정한 결과, 최종적으로 α t = A · S A T t B
선택된 모델을 이용하여 미래 기후변화 시나리오에 따른 영향 분석의 예를 확인 한 결과, 서울지점의 경우 지표면 기온이 증가함에 따라 확률강우량이 증가할 가능성이 매우 높음을 살펴볼 수 있다. 또한, 기상변수를 고려한 비정상성 모델을 구성할 경우 기상변수의 분포에 따른 확률강우량의 확률분포함수를 직접 구성할 수 있게 되므로, 기후변화에 따른 확률강우량 추정의 불확실성을 정량적으로 분석하는데 효과적일 것으로 판단된다.
본 연구를 통해 살펴본 기상변수를 고려한 빈도해석에 의한 접근방법은 극한 강우에 대한 기후변화의 영향을 살펴보기 위한 방법 중 하나로 이용 될 수 있을 것으로 판단된다. 다만 본 연구에서는 GEV 분포형의 매개변수 중 축척매개변수를 적용하여 연구를 진행하였으며, 공변량을 선택하는 기준 또한 다양한 방법으로 선택 될 필요가 있다. 또한 추후 연구를 통해 다른 매개변수를 공변량으로 적용한 결과와 비교할 필요가 있을 것으로 판단된다.
Fig. 4
Relationship Between Extreme Daily Rainfall and the Daily Surface Air Temperatures During Wet Days in Summer at Seoul
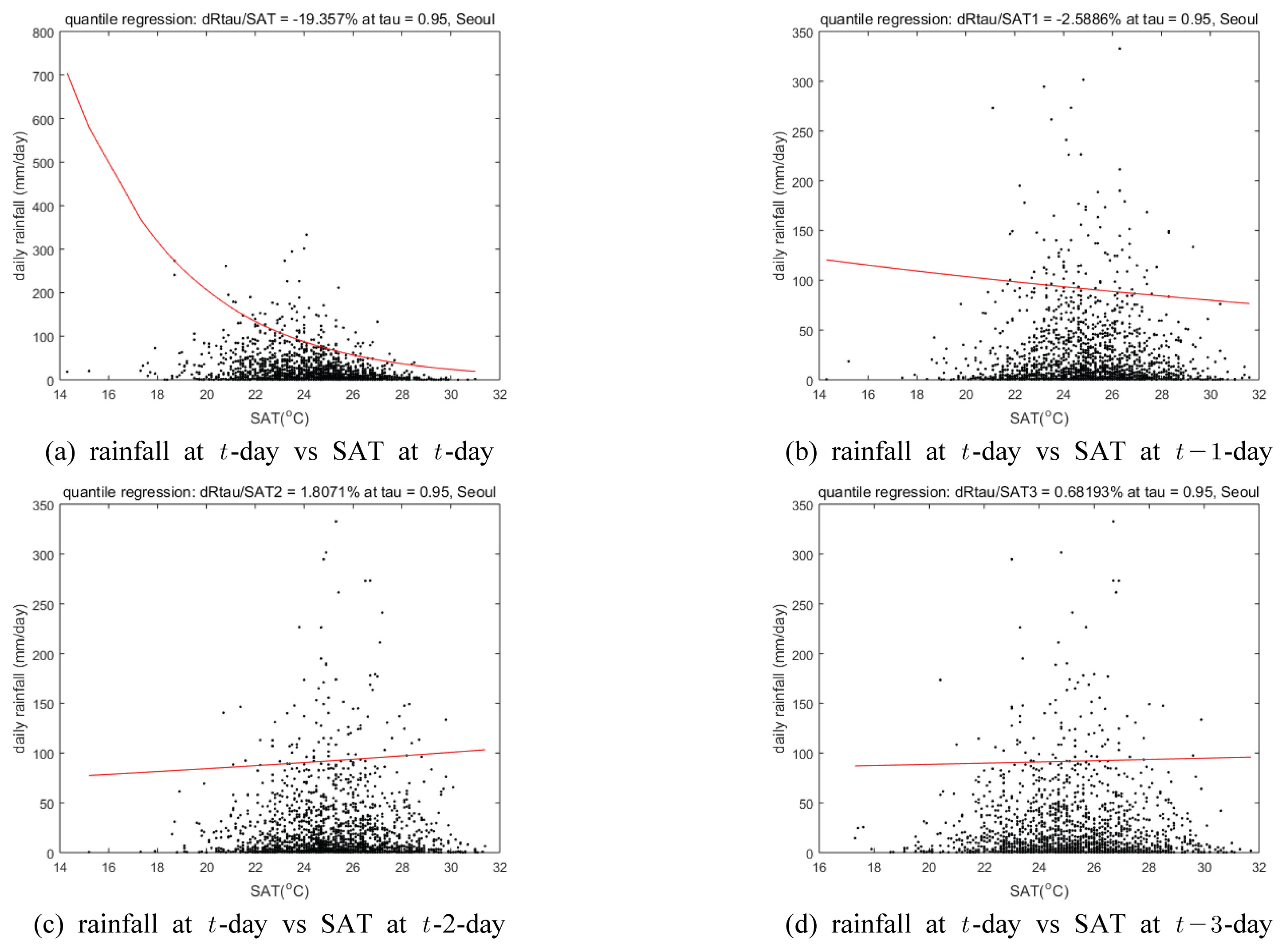
Fig. 5
Relationship Between Extreme Daily Rainfall and the Daily Dew-point Temperatures During Wet Days in Summer at Seoul
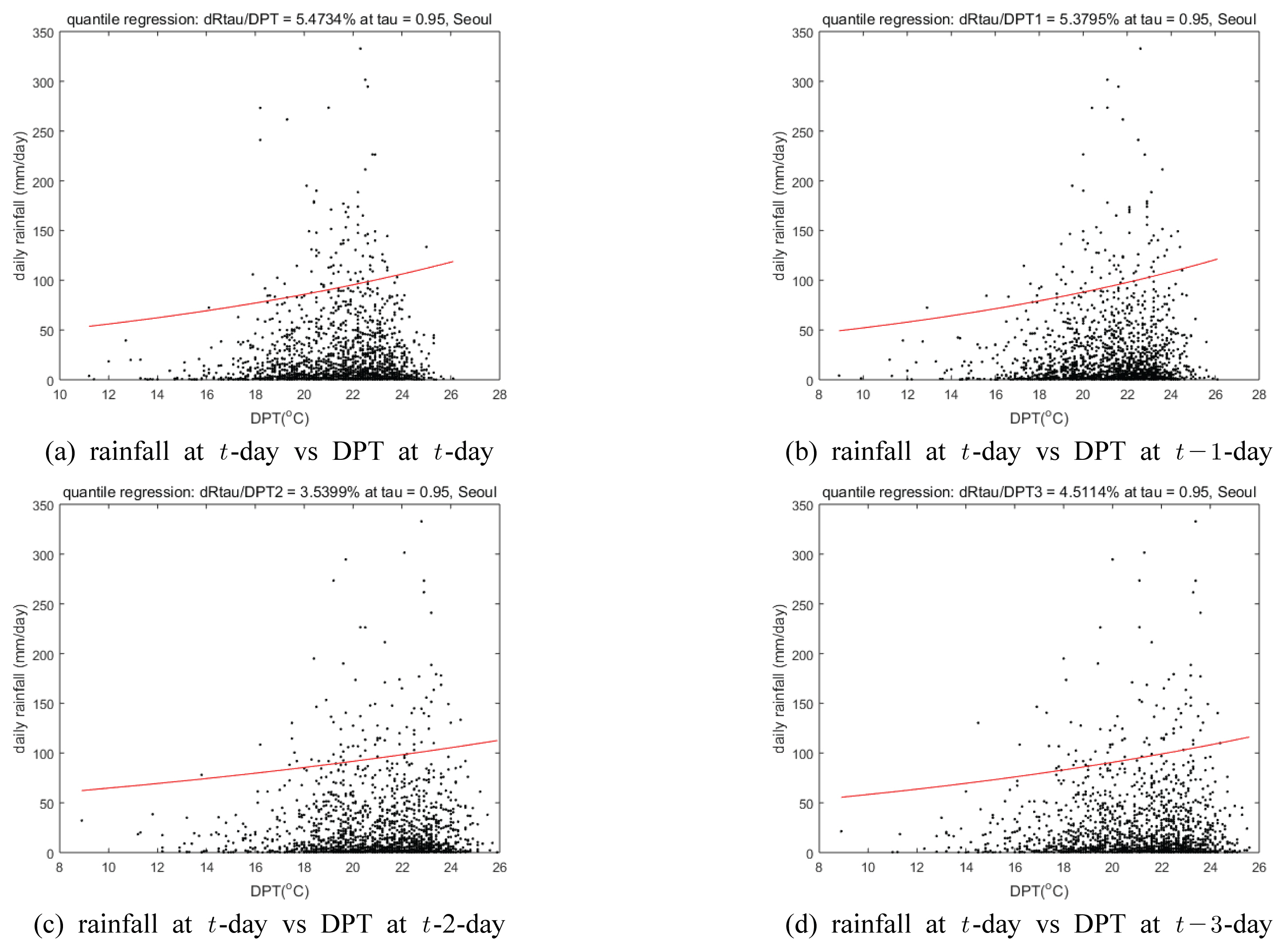
Fig. 7
95%, 99%, and 99.5% Non-exceedence Monthy Maximum Daily Rainfall Depth for Stationary Model and Non-stationary Model

Fig. 8
Distributions for Stationary Model (stationary) and Non-Stationary Model for Low (NS(08/2008)) and High (NS(07/2001)) Daily Rainfall Depth in Summer Months
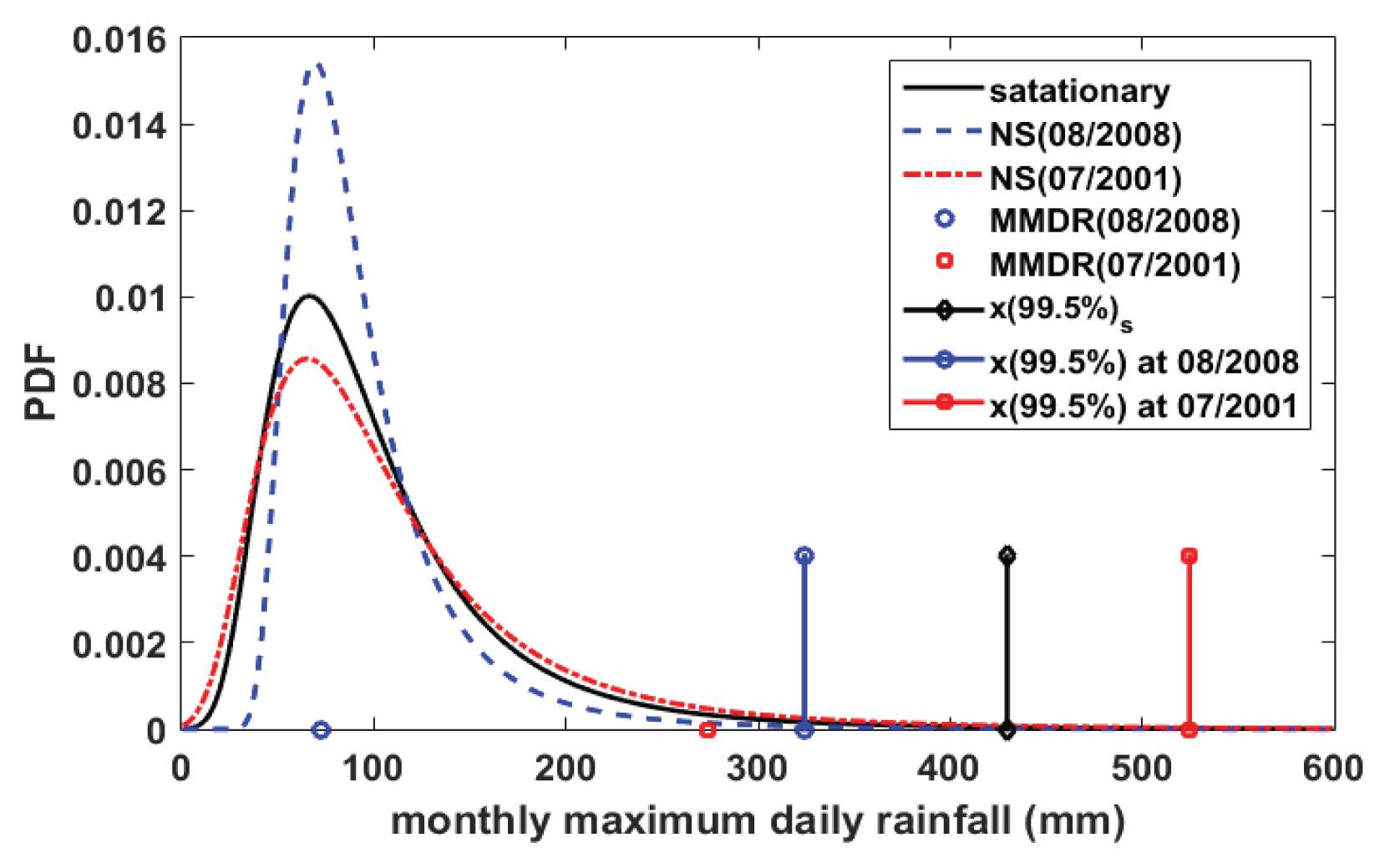
Fig. 9
Distributions of 99th Quantile Value from Non-stationary Model Under Present Scenario, SAT 1 °C-up Scenario, and SAT 3 °C -up Scenario

Table 1
Generalized Extreme Value Parameters and AIC of Summer Monthly Maximum Daily Rainfall
Table 2
Probability of Exceeding Stationary Quantiles for Stationary Model and for Selected Low and High Maximum Daily Rainfall Months for Non-stationary Model
| Stationary quantile (mm/day) | P[X > x(1−p)] (%) | ||
|---|---|---|---|
| stationary | Low at 08/2008 | High at 07/2001 | |
| x99= 358.3 | 1 | 0.34 | 1.85 |
| x90= 178.0 | 10 | 4.77 | 13.64 |
| x50= 87.4 | 50 | 45.12 | 52.66 |
| x10= 44.4 | 90 | 98.44 | 87.55 |
References
Aissaoui-Fqayeh, I, El-Adlouni, S, Ouarda, TBMJ, and St-Hilaire, A (2009) Non-stationary lognormal model development and comparison with the non-stationary GEV model. Hydrological Sciences Journal, Vol. 54, No. 6, pp. 1141-1156.

Akaike, H (1974) A new look at the statistical model identification. IEEE Transactions on Automatic Control, Vol. 19, No. 6, pp. 716-723.

Ali, H, and Mishra, V (2017) Contrasting response of rainfall extremes to increase in surface air and dewpoint temperatures at urban locations in India. Scientific Reports, Vol. 7, No. 1, pp. 1228.



El Adlouni, S, Ouarda, TBMJ, Zhang, X, Roy, R, and Bobée, B (2007) Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resources Research, Vol. 43, No. 3, W03410. pp. 1-13.



Hosking, JRM (1990) L-moments: Analysis and estimation of distributions using linear combinations of order statistics. Journal of the Royal Statistical Society Series B (Methodological), Vol. 52, No. 1, pp. 105-124.

Kim, H, Kim, T, Shin, H, and Heo, J (2017) A study on a tendency of parameters for nonstationary distribution using ensemble empirical mode decomposition method. Journal of Korea Water Resources Association, Vol. 50, No. 4, pp. 253-261.

Kunkel, KE, Pielke, RA Jr, and Changnon, SA (1999) Temporal fluctuations in weather and climate extremes that cause economic and human health impacts: A review. Bulletin of the American Meteorological Society, Vol. 80, No. 6, pp. 1077-1098.



Lee, O, and Kim, S (2018) Estimation of future probable maximum precipitation in Korea using multiple regional climate models. Water, Vol. 10, No. 5, Article No. 637.

Lepore, C, Veneziano, D, and Molini, A (2015) Temperature and CAPE dependence of rainfall extremes in the eastern United States. Geophysical Research Letters, Vol. 42, No. 1, pp. 74-83.

O’Gorman, PA (2012) Sensitivity of tropical precipitation extremes to climate change. Nature Geoscience, Vol. 5, No. 10, pp. 697-700.

Pujol, N, Neppel, L, and Sabatier, R (2007) Regional tests for trend detection in maximum precipitation series in the French Mediterranean region. Hydrological Sciences Journal, Vol. 52, No. 5, pp. 956-973.

- TOOLS
-
METRICS

-
- 1 Crossref
- 3,610 View
- 50 Download
- Related articles in KOSHAM
-
Non-Stationary Frequency Analysis and Uncertainty of Heat Wave Events2021 February;21(1)
Non-stationary Frequency Analysis of Extreme Sea Level Using POT Approach2018 December;18(7)
Behavior Analysis of Pile-bent Piers Using Steel Pipe Piles2018 April;18(3)
Nonstationary Frequency Analysis Using a Hierarchical Bayesian Model2015 October;15(5)